基于FPGA的北斗驯服铷原子频标装置的研制

王亚军， 张 磊， 谷 扬， 黄 艳， 康婷婷

(北京市计量检测科学研究院，北京 100029)

1 引 言

在现代信息社会，导航定位和授时系统是最重要也是最关键的位置和信息服务[1,2]。而时钟同步是精密授时的根本保证。铯钟和铷钟是常用的同步原子时钟[3]。虽然铯原子钟频率稳定度好，精度高，但是价格昂贵，使用寿命短[4]；而铷原子钟长寿命己得到验证，体积小，重量轻，预热时间短，且价格相对较低，通过一定的技术手段与卫星时钟同步，可以长期保持较好的稳定度和准确度，保证较高授时准确度[5]。所以，研制可靠，准确和稳定的北斗驯服铷原子钟系统显得十分重要和迫切。

本文对我国的北斗卫星导航系统的精密授时信号进行测试和分析，并研究了驯服铷原子钟技术，设计和研制体积更小、多路输出的北斗系统驯服的铷原子频标装置，与铯原子钟频率进行比对，取得了良好效果。对于加强和提高卫星同步授时技术，完善和升级卫星同步授时配套实施，积累技术能力。

2 铷钟驯服装置原理和系统设计

2.1 铷原子钟守时原理

铷原子频标利用铷基态超精细能级之间的跃迁频率作为参考频率，把内部压控振荡器输出的 10 MHz 通过调相、倍频后在量子鉴频器中与参考频率鉴频，当压控振荡器的频率与跃迁频率相差很小时，铷原子产生能级跃迁[6]。跃迁时铷灯发出的光被大量吸收，导致照射到光电转换器上的光线减弱[7]。伺服电路提取变化的光强信号作为误差纠偏电压，使压控振荡器被铷原子参考频率锁定，从而保证铷原子频标输出的10 MHz频率[8]。

研制多路输出北斗驯服铷原子频标装置，利用北斗卫星时频驯服铷原子钟输出的1 Hz信号，使用铷原子钟输出的1 Hz信号跟踪北斗卫星时频的1 Hz脉冲信号，当卫星信号丢失时，时钟系统自动切换到铷原子钟保持模式输出，以保证整个系统的高精度稳定授时。该系统包括硬件电路，控制软件和上位机接收，其结构框图如图1所示。

图1 铷钟驯服结构框图Fig.1 General chart of rubidium clock taming structure

硬件电路由铷钟模块、时间间隔测量电路、秒脉冲同步、控制和存储电路、多路输出电路、接收机等组成；控制软件由频率控制、数据采集、数据处理和数据传输等部分组成；上位机接收包括数据存储和数据接收等模块。其中设计高精度的时间间隔测量模块是实现和保证铷钟驯服的关键模块。

2.2 高精度时间间隔测量方法

目前，实现高精度时间间隔测量的方法有多种，如模拟内插法、时间幅度转换法、游标法、延迟线内插法等[9]。这几种测量方法测时分辨率最高可以达到几个ps量级。对于一个给定的时间间隔，为获得动态范围大、精度高的时间间隔测量，通常方法是用频标信号进行填充，然后用计数器计数，根据测得的标频脉冲个数，计算出时间间隔，其基本原理如图2所示。

图2 时间间隔计数原理Fig.2 Principle of time interval counting

在计数过程中，由于填充脉冲与时间间隔构成的闸门边沿的相位关系具有随机性，因此会产生±1个计数误差[10]。为了减小测量电路分辨率带入的±1个计数误差，为此，采用了计数法与延迟线内插法相结合的方法。以计数法实现“粗”计数，以延迟线内插法实现“精”时间测量。根据图2得出任意待测时间间隔Tx可以表示成如下形式:

Tx=N·T+ΔT1-ΔT2

(1)

式中：T为时基脉冲周期；N·T为对待测时间间隔Tx的粗测量；ΔT1-ΔT2为对时间间隔的细测量。计数法是传统的时间间隔测量方法，其本质就是一个计数器，基本功能是对时间间隔覆盖的参考频率周期T的个数进行计数，即测量时间间隔表达式中N·T中的N。测量时，一般是在某一固定闸门时间里，利用标频10 MHz脉冲进行填充，对标频填充脉冲的个数进行计数。在计数过程中，必然会在短时间间隔ΔT1和ΔT2处出现最大±1个填充脉冲周期的计数误差。这2个零头时间就可以进一步由延迟线内插法实现。

延迟线内插法的突出优点可实现单片集成，可以在FPGA或专门的ASIC上实现[11]。本设计采用Altera公司的CycloneII系列器件EP2C5T144I6N来实现，该器件精度高，可配置的逻辑模块规模大，调试简单，功耗低，支持2个工作线程，多工作模式，工作方式灵活，能实现双通道250 ps分辨率或单通道125 ps分辨率[12]。可精确测量时间、相位、频率等物理量。设计的时间间隔测量框图如图3所示。

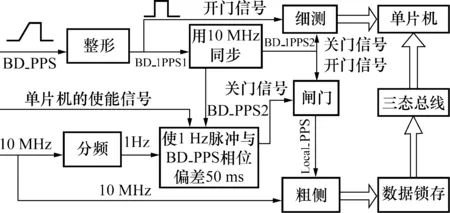
图3 时间间隔测量框图Fig.3 Block diagram of time interval measurement

图3中BD_PPS2作为粗计数开门信号的同时也是细计数的关门信号。另外，BD_PPS2信号是BD_PPS1经10 MHz同步产生的，而本地秒脉冲Local_PPS的发生也来自10 MHz时基，因此两者相关(上升沿同时与10 MHz上升沿重合)。这样，用10 MHz进行填充时粗计数始终为100 ns的整数倍，不存在任何余量，从而可以避免求取ΔT2的过程，同时也实现了粗细测量的无缝连接。测量时序图如图4所示。

图4 时间间隔测量时序图Fig.4 Time sequence diagram for time interval measurement

2.3 铷钟驯服电路设计

将设计的时间间隔测量应用到驯服铷原子钟系统中，其具体过程简单来说以接收机输出的1 Hz脉冲信号为参考信号，通过驯服电路控制铷原子钟，使得铷原子钟的1 Hz脉冲信号输出不断跟踪外部输入的1 Hz脉冲信号。铷原子钟驯服原理如图5所示。

图5 铷原子钟驯服电路原理框图Fig.5 Principle block diagram of rubidium atomic clock taming circuit

采用卫星时钟接收机输出的1 Hz信号作为铷原子钟的输入参考标准，铷原子钟输出的10 MHz经分频得到的1 Hz脉冲信号与参考信号在鉴相器中进行比较，将二者的相位差送到处理器中进行运算，经过数字滤波算法，减小卫星1 Hz脉冲信号的抖动，根据铷原子频标的控制模型，产生相应的控制信号，对铷原子钟的频率进行微调[13]。铷原子钟通过接收外部的串口信号，修正自身的时间，使得铷原子钟输出的1 Hz脉冲信号不断跟踪外部输入的1 Hz脉冲信号，同时提供串口对外输出信号。一旦外部的1 Hz脉冲校时信号和串口信号消失，驯服系统可以根据之前存储的数据提供短时的守时数据，原子钟即可提供标准的时间信号输出。

2.4 铷钟驯服软件设计

系统软件由单片机程序控制。单片机程序是一个简单的实时多任务中断查询程序，其主流程图如图6所示。

图6 系统程序主流程图Fig.6 Main flow chart of system program

3 测试数据分析和比较

本装置在调试过程中，以铯原子钟输出时频信号为参照标准，对铷钟的一些关键信息参数进行了连续两周的稳定可靠性比对测试。铷钟驯服前后10 MHz频率准确度曲线对比如图7所示。

图7 铷钟驯服前后10 MHz频率准确度对比曲线Fig.7 Comparison curve of 10 MHz frequency accuracy before and after rubidium clock taming

通过测试数据和图7曲线可以得出，选用的FEI公司型号为FE5650A的铷钟在驯服前输出的10 MHz频率准确度约为6.73×10-12，日波动大约为3.33×10-11。研制的驯服装置，连接天线接收北斗卫星数据，去除开机后频率不稳定数据，铷钟驯服后的10 MHz频率准确度大约为1.5×10-13，开机特性为3.0×10-13，明显优于驯服之前的频率准确度。

随着该装置对铷钟驯服时间的越久，铷钟的频率波动就越来越小，频率稳定度越来越好。测试铷钟驯服后的频率稳定度曲线如图8所示。

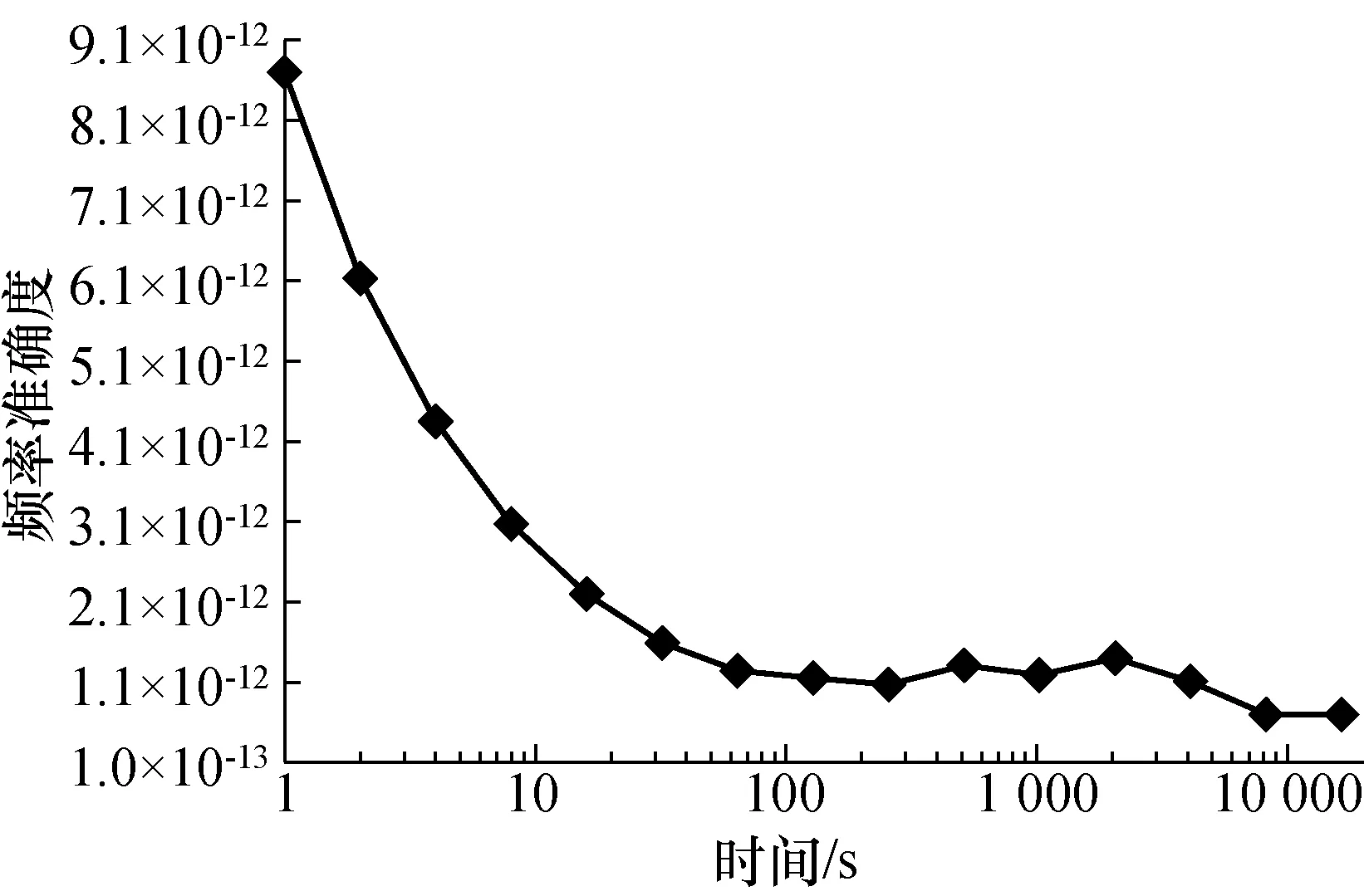
图8 铷钟驯服后的稳定度曲线Fig.8 Stability curve of rubidium clock after taming

从图8可以看出，当在1 s时，频率稳定度为8.70×10-12，在160 s时，频率稳定度为2.20×10-12，在4 100 s时，频率稳定度达到1.11×10-12，在8 190 s时，频率稳定度达到6.97×10-13，并在此之后稳定度基本趋于平稳。同时研制的装置通过串口向上位机发送当前铷钟驯服状态以及连接卫星数量等情况。

4 结 论

通过研究铷原子驯服技术，设计了基于FPGA技术的多路输出BD驯服铷原子频标装置。以铯原子钟时间频率为参考，通过对铷钟驯服前后的数据进行多次比对测试。测试数据表明，该装置无论在频率的准确度还是稳定度均达到10-13量级，而且该装置对外输出除了通用的串口RS232，还增加了RS485，CAN口，以太网口等多种对外接口，提高和拓宽了该装置的适用场合，对后续进一步提高铷原子钟的驯服和同步技术提供了技术依据。

[参考文献]

[1] 陈智勇, 韩蒂, 庆毅, 等. 面向时间应用的可驯服铷钟[J]. 宇航测试技术, 2013, 33(1): 33-34.

Chen Z Y, Han D, Qing Y,etal. A Discipline rubidium oscillator for timing application[J].JournalofAstronauticMetrologyandMeasurement, 2013, 33(1): 33-34.

[2] 朱江, 李振华. 卫星导航接收机时延测定技术研究[J]. 计量学报, 2019, 40(5): 910-913.

Zhu J,Li Z H. Research on Time Delay Measurement Technology for Satellite Navigation Receivers[J].ActaMetrologicaSinica, 2019, 40(5): 910-913.

[3] 王玉琢, 张爱敏, 张越, 等. 一种原子钟频率稳定度的估计方法[J]. 计量学报, 2018, 39(3): 397-400.

Wang Y Z, Zhang A M, Zhang Y,etal. An estimation method of frequency stability of atomic clock[J].ActaMetrologicaSinica, 2018, 39(3): 397-400.

[4] Kirsten L. Strandjord; Penina Axelrad Improved prediction of GPS satellite clock sub-daily variations based on daily repeat[J].SpringerJournal, 2018, 3(18): 1-13.

[5] Wang B, Lou Y D, Liu J N,etal. Analysis of BDS satellite clocks in orbit[J].SpringerJournal, 2018, 4(15): 783-794.

[6] 尹文芹, 施韶华, 文音华, 等. 基于FPGA实现TDC的布局布线优化方法研究[J]. 时间频率学报, 2018, 41(1): 27-36.

Yin W Q, Shi S H, Liu Y H,etal. Optimization of digital TDC circuit routing based on FPGA[J].JournalofTimeandFrequency, 2018, 41(1): 27-36.

[7] 闫菲菲, 马红皎, 何在民, 等. 基于FPGA和TDC芯片的高精度时间间隔计数器研制[J]. 时间频率学报, 2019, 42(1): 33-42.

Yan F F, Ma H J, He Z M,etal. Development of high precision time interval counter based on FPGA and TDC chip [J].JournalofTimeandFrequency, 2019, 42(1): 33-42.

[8] 罗莹, 张志伟, 杨宁, 等. 基于锁相环的解调技术研究[J]. 计量学报, 2015, 36(4): 432-435.

Luo Y, Zhang Z W, Yang N,etal. Research on demodulation technology based on PLL[J].ActaMetrologicaSinica, 2015, 36(4): 432-435.

[9] 魏煜秦, 孔洁, 杨海波, 等. 基于FPGA的时间间隔测量设计与实现[J]. 原子能科学技术, 2017, 51(10): 1893-1897.

Wei Y Q, Kong J, Yang H B,etal. Design and Implementation of Time Interval Measurement Based on FPGA[J].AtomicEnergyScienceandTechnology, 2017, 51(10): 1893-1897.

[10] 孟令达, 施韶华, 赵志雄, 等. 多通道时间间隔测量分析系统的设计与实现[J]. 时间频率学报, 2017, 40(2): 80-86.

Meng L D, Shi S H, Zhao Z X,etal. Design and implementation of multichannel time interval measurement and analysis system[J].JournalofTimeandFrequency, 2017, 40(2): 80-86.

[11] 李泽宁, 温淑敏, 何磊磊, 等. 时间频率信号精密测量计数器的设计与实现[J]. 无线电通信技术, 2017, 43(6): 97-102.

Li Z N, Wen S M, He L L,etal. Design and implementation of precision measuring counter for time and frequency signal[J].RadioCommunicationsTechnology, 2017, 43(6): 97-102.

[12] 朱江淼, 孙盼盼, 高源, 等 原子钟频差数据去噪算法的研究[J]. 计量学报, 2017, 38(4): 499-503.

Zhu J M, Sun P P, G Y,etal. Research on the denoising algorithm of frequency difference data of atomic clock[J].ActaMetrologicaSinica, 2017, 38(4): 499-503.

[13] 高帅, 谷力, 刘烈曙. 高精度时间间隔测量在时间比对和频率校准中的应用[J]. 现代导航, 2016 , 7(4): 239-245.

Gao S, Gu L, Liu L S. Application of high precision time interval measurement in time comparison and frequency calibration[J].ModernNavigation, 2016 , 7(4): 239-245.