Matlab 在圆形断面特征水深计算中的应用

李 蕊

（杨凌职业技术学院，陕西 杨凌 712100）

1 引言

水力计算中经常会遇到圆形断面正常水深、临界水深和收缩水深的求解问题，其实质是求解含参变量的非线性方程或超越方程，此类方程没有求根公式，不能直接计算，传统的计算方法主要有：①试算法，即利用试探法与二分法进行试算，计算繁杂，工作量大；②图表法，即利用已经制好的大量图表求解，由于此类图表种类多，使用麻烦，而且精度欠佳。

近十多年来，国内外专家学者针对圆形断面特征水深的计算问题，进行了大量研究，他们的研究成果主要集中在两个方面：①引入无量纲水深，通过对特征水深方程的数学变换，得到无量纲水深的近似直接计算公式[1～9]；②采用逐次逼近原理进行迭代计算，通过选取合适的迭代初值和迭代方程计算特征水深[10～12]；另外，也有部分专家学者采用其它方法计算特征水深，如殷彦平等[13]将圆形断面正常水深问题转化为非线性约束优化问题，应用混合模式搜索法求解水深；张新燕等[14]利用非线性函数模型，通过Marquardt 法建立了正常水深的直接计算公式。另外，这些研究成果大部分都集中在圆形断面的临界水深和正常水深的计算中，对于圆形断面收缩水深的计算研究较少。

非线性代数方程的求解大部分都可以通过数学软件来实现，Matlab 以其强大的编程及计算功能而被广泛地应用于求解非线性代数方程中。

Matlab 是集数值分析与计算、微积分与矩阵运算、工程与科学绘图、数字图像处理、数字信号处理、语言编程于一体的一款工程软件。Matlab 操作简单，易于掌握。文中采用Matlab 中查找函数零点的命令fzero 及语言编程，对圆形断面临界水深、正常水深和缩水深进行编程计算，其程序简洁明了，易于操作，而且效率和精度都非常高。

2 用Matlab 求解圆形断面特征水深

2.1 圆形断面临界水深的计算

2.1.1 圆形断面临界水深的求解公式

水力学中临界流的基本方程为：

如图1 所示，圆形断面的水力要素分别为：

图1 圆形过水断面

过水断面面积：

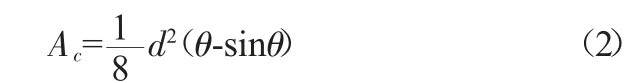
水面宽度：

临界水深：

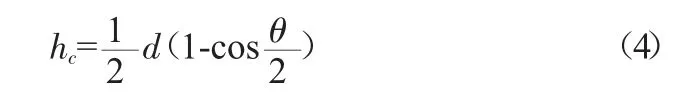
式中：Q 为过水流量，m3/s；Ac为临界流对应的过水断面面积，m2；Bc为水面宽，m；g 为重力加速度，通常取9.81 m3/s；a 为流速分布不均匀系数，通常取1.0；θ 为临界水深对应的圆心角，rad；d 为圆形断面直径，m。

将式（2）、式（3）代入式（1）得：

将上式变形得：

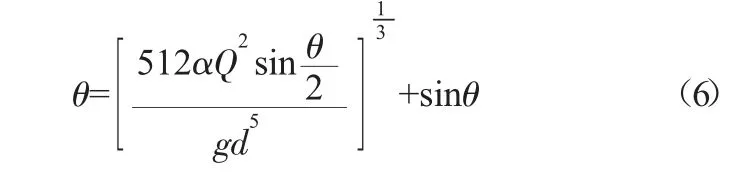
由此可见：式（6）为关于θ 的含参数的超越方程，理论上无解析解。因此可以利用Matlab 编程求出θ，然后代入式（4）可求出临界水深hc。

2.1.2 工程实例

以文献[3]为例，某圆形断面的引水式电站输水隧洞，洞径d=15.0 m，求设计流量Q=1 m3/s 时的临界水深。

利用Matlab 求解圆形断面临界水深程序如下：

在Matlab 语言中：alpha 表示α，theta 表示θ.

>>syms alpha Q g d theta

>>alpha=1.0；

>>Q=1；

>>g=9.81；

>>d=15；

>>f=@ (theta)(512*alpha*Q^2*sin (theta/2)./(g*d^5)).^(1/3)-theta+sin(theta)；

>>theta=fzero(f,[0.000001 2*pi])

theta=0.5440

>>hc=1/2*d*(1-cos(theta/2))

hc=0.2757

即临界水深hc=0.2757。

用孙建公式、王正中公式和赵延风公式分别计算本例，结果见表1。

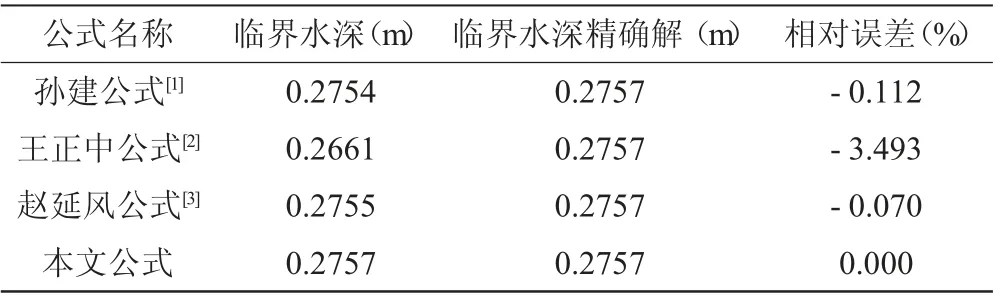
表1 临界水深不同计算公式误差比较

2.2 圆形断面正常水深的计算

2.2.1 圆形断面正常水深的求解公式

水力学中圆形断面均匀流方程为：

圆形断面的水力要素为：

①过水断面面积，根据式（2）计算。

②湿周：

③正常水深：

式中：n 为粗糟系数；Q 为过水流量，m3/s；i 为底坡；Ac为发生均匀流时的过水面积，m2；Bc为水面宽度，m；p 为湿周；hc为均匀流水深，m；d 为圆形断面直径，m；θ 发生均匀流时的圆心角，rad。

将式（2）、式（9）代入式（8）中得：

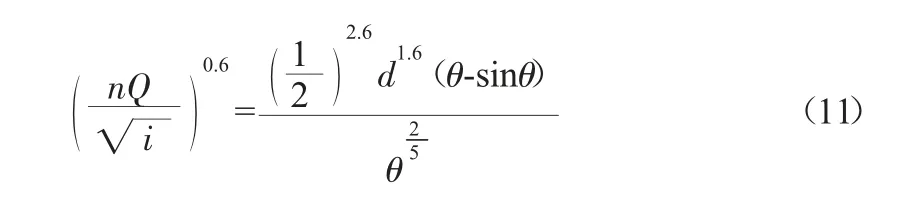
将上式变形得：

由此可见，式（12）为关于θ 的含参数的超越方程，理论上无解析解。因此可以利用Matlab 编程求出θ，然后代入式（10）可求出正常水深hk。

2.2.2 工程实例

以文献[7]为例，某圆形断面的引水式电站输水隧洞，已知断面底坡，i=0.001 粗糟系数n=0.015，洞径d=15.0 m，求设计流量Q=840 m3/s 时的正常水深。利用Matlab 求解圆形断面正常水深程序如下：

在Matlab 语言中：theta 表示θ，i 表示虚数单位，所以i 用I 表示，以示区别。

>>syms n Q I d theta

>>n=0.015;

>>Q=840;

>>I=0.001;

>>d=15;

>>f=@ (theta)(2^2.6* (n*Q/sqrt(I))^0.6*theta^0.4./d^1.6)-theta+

sin(theta);

>>theta=fzero(f,[0.000001 2*pi])

theta=4.2640

>>hk=1/2*d*(1-cos(theta/2))

hk=11.4915

即正常水深hk=11.4915。

用文献[1]和文献[2]中的公式分别计算本例，结果见表2。

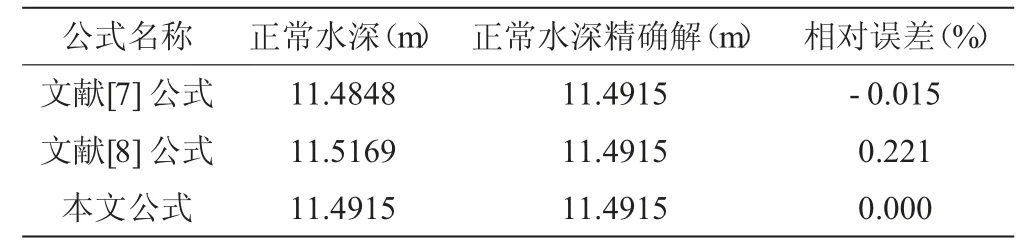
表2 正常水深不同计算公式误差比较

2.3 圆形断面收缩水深的计算

2.3.1 圆形断面收缩水深的求解公式

水力学中圆形断面收缩流的方程为：

圆形断面的水力要素为：

①过水断面面积，计算见式（2）。

②收缩水深：

式中：E0为上游断面总水头，m；Q 为过水流量，m3/s；hs为收缩水深，m；d 为圆形断面直径，m；φ为流速系数；θ 发生收缩流时的圆心角，rad。

将式（2）、式（14）代入式（13）中得：

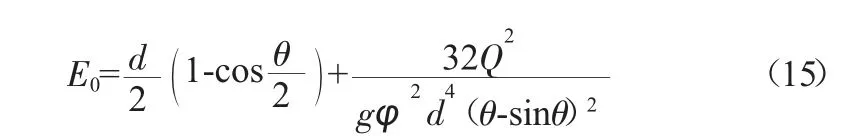
将上式变形得：

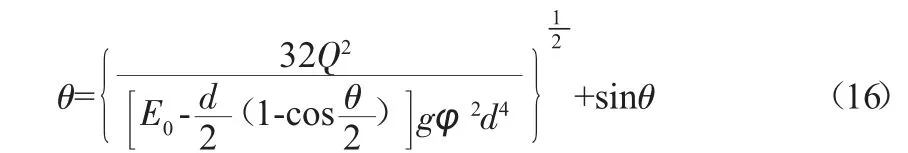
求出θ 后，代入式（14）可求出收缩水深。

由此可见，式（16）为关于θ 的含参数的超越方程，理论上无解析解。因此可以利用Matlab 编程求出θ，然后代入式（14）可求出收缩水深.

2.3.2 工程实例

以文献[9]为例，已知坝(闸)前断面总水头E0=12 m，圆形断面直径d=15.0 m，流速系数φ=0.95,求设计流量Q=500 m3/s 时的收缩水深。

利用Matlab 求解圆形断面临界水深程序如下：

在Matlab 语言中：phi 表示φ，theta 表示θ。

>>syms phi Q g d theta E0

>>g=9.81;

>>phi=0.95;

>>Q=200;

>>d=15;

>>E0=12;

>>f=@ (theta) (32*Q^2./ ((E0-d* (1-cos (theta/2))./2)*g*phi^2*d^4))^(1/2)-theta+sin(theta);

>>theta=fzero(f,[0.000001 4.39])

theta=1.5367

>>hs=0.5*d*(1-cos(theta/2))

hs=2.1071

即收缩水深hs=2.1071。用赵延风公式计算本例，结果见表3。

表3 收缩水深不同计算公式误差比较

3 结论

从表1、表2 和表3 的误差比较可以看出，应用Matlab 数学软件求解的圆形断面的正常水深、临界水深和收缩水深，不仅程序简单明了，而且计算精度高，方法更容易掌握。Matlab 作为一种强大的工程软件，必将会广泛应用在水力计算和水利设计中。