基于ArcGIS 软件对河道高程数据插值方法的对比

黄一帆，李文辉，李凯博

（宝鸡市水利水电规划勘测设计院，陕西 宝鸡 721000）

ArcGIS 软件空间插值方法在学术研究领域已广泛应用，其对数据信息进行预测的精准度已被广大学术研究认可，但在实际设计工作中却很少涉及。水利设计工作在洪水演算、水面线计算、淹没影响、库容计算及风险分析等常涉及的工作方面均需要丰富的河道高程基本信息，通过从中提取河道断面信息用于后续水利工程设计[1]。目前设计工作领域常利用实测河道地形图进行人工插值，如果缺乏放样测设点，插值出来的河道高程数据误差极大且工作量大，其低精度的数据对河道相关工程设计的准确性影响极大，单纯的测量图也很难直观分析到地形走势及河道滩面局部特性，因此需要人为进行逐点分析描绘高程点以此来分析河道走势和河床特性。本文拟选用ArcGIS 软件中反距离权重和普通克里金两种插值方法对选择的渭河防洪纪念碑段河道进行插值分析，并利用预留点位校验不同插值法的模拟结果，最终为实际设计工作推荐更为合理简便的插值方法。

1 ArcGIS 软件空间插值方法

1.1 IDW 插值法

IDW 插值法[2]原理为假设位置近的未知高程点影响大于距离远的已知高程点，差值点与样本点间距为权重加权平均后距离插值点近的点权重偏大，其主要依据是反距离幂值，幂参数可依据距离来控制已知点位对插值的影响[3]，原理公式如下：

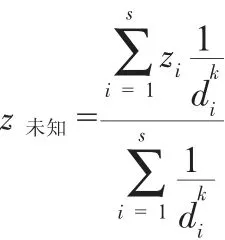
1.2 Kriging 插值法

Kriging 插值法是一种常用插值法，其包括普通Kriging、泛Kriging 和简单Kriging 三种基本方法，其原理为协方差函数对数据进行空间建模和预测插值，是一种典型的地统计学方法，本文选用普通Kriging 进行插值处理[4]。基本公式如下：

2 实例应用

2.1 区域河道现状及数据来源

研究区所在河段为渭河防洪纪念碑河段，其地处宝鸡峡大坝下游约3.5 km 处，上游有硖石河支流汇入，流域面积45.2 km2，平均比降3‰，多年平均降水量695.8 mm，多年平均气温12.9℃，该段河道地处渭河峡谷段至陕西关中平原段过渡地带，河道特性基本呈过渡段河道特性，河势稳定、滩槽明显、干流中洪合一、主槽归顺，平面摆动不大，该段河道内基本未经开发利用，原始地形数据为多年河道演变冲淤的自然结果，对插值训练模型的影响因素也较小。研究区共选取河段范围内363 个高程实测数据点作为研究基础数据，其中随机选取20 个点作为检验数据（▲），剩余343 个数据（○）分别采用IDW 和Kriging插值法作为训练建模数据。首先对原始数据进行处理，将Excel表格数据导入ArcGIS 软件中，将其转化为Shp 文件（图1），第二步将Shp 文件转化为Dem 文件，对河道原始数据进行分析，对数据的可靠性及河道真实情况反映进行分析，最后在3D Analyst 模块中分别选用IDW 和普通Kriging 插值法对河道进行空间插值模拟训练，通过改变内部参数得到模拟结果相对较为准确的模型。

图1 研究区训练点和检验点位置图

2.2 训练模型评价

（1）河道地形分析

图2 研究区河道数据分析图

在对研究区河道基础高程数据进行空间插值处理前首先对高程数据呈现的河道现状进行分析，通过将Shp 数据在3D Analyst 模块下转换为Dem 数据后，导入ArcScene 中绘制三维河道模型，为凸显河道现状将纵向垂直夸大比例选择为20倍。从图2 中不断转换视角观察河道绘制结果分析得到：最上游断面和左右岸数据偏高，平均高程在601 m，该处分别为桥墩和左右岸堤防；河道内河槽清晰可见，主流靠近左岸，滩面不断有坡面起伏，河道摆幅不大，均符合该段河道现状，因此该段高程数据真实可靠，可以用于进行之后空间插值分析计算。

（2）训练结果分析

图3 两种插值法训练结果分布图

表1 两种插值法训练结果精度表

图3 中（a）为IDW 插值法训练结果，（b）为Kriging 插值法训练结果，由表1 和图3 分析得知，分布图中地形走势两种方法表现结果基本一致，在南岸河道IDW 插值法高程偏低，且在上游部位高程点呈孤点分布，原因为IDW 插值法在训练结果关联性较差，大部分反映为局部真实值，对离散点较少改变原数据，而Kriging 插值法成图较IDW 插值法光滑平顺，孤点较少，在河道中下游部位等高线表现较为连贯光滑，在河道上游和南岸区域模拟数据结论较真实地形接近，其数据之间的关联性也较高，原因为其对离散点高程数据进行了重新模拟，从精度角度分析，IDW 插值法较Kriging 插值法精度也略低。

（2）检验点分析

通过随机选取预留的20 个检验点数据对两个插值训练模型进行检验，结果见图4。由图4 可以看出总体上在点位85#、161#、231#和303#训练模拟结果较真实值偏低，最大差距在4.15 m，总体模拟趋势值偏高，模拟误差中最大值为IDW 法插值的174#点位，误差最小的为Kriging 插值法模拟的339#点位，Kriging 和IDW 插值法误差平均值分别为1.9 m 和3.2 m，综合上述分析得到结论Kriging 插值法计算出来的插值结果更接近真实值，仅在局部点位不如IDW 插值结果精度高，IDW 插值法计算结果波动偏大，误差值拟合精度较差，因此，在本例中预测效果最佳的方法为Kriging 插值法。

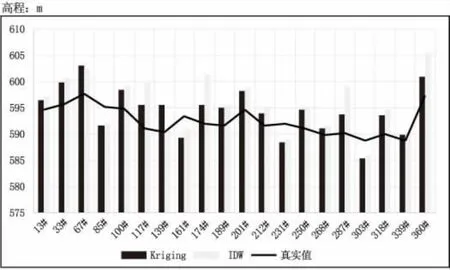
图4 检验点真实值与模拟点对比图

通过上述对比分析总结，本次模拟训练在ArcGIS 的不同插值方法中训练结果略有差距，结论显示Kriging 插值法较IDW 插值法插值精度偏高，但在与预留检验点对比分析中误差值偏大，原因是本次选取点位数量偏少及其代表性不强导致，加之河道中高程点可变性较强，与河势冲淤变化影响相关，因此导致本次模拟结果误差偏大，但总体上显示河道走势和高程分布与真实值偏差不大，其可在河势演变及断面分析的实际应用中提供帮助。

3 结论

本文通过对选取渭河河道基础高程数据，利用ArcGIS 软件空间插值方法训练结果和检验点对比分析可知：

（1）ArcGIS 软件空间插值方法较传统设计工作常用的方法工作量大大降低，其图面直观，可视化水平高，ArcGIS 软件的空间建模能力能有效对河道数据进行准确预测。

（2）通过在ArcScene 中绘制的河道三维模型可以更直观的分析河道现状，预测存在的风险。本文着重进行了数据空间处理后与河道现状相符性的分析，同时也可延伸至坡向、淤积、坡度变化率甚至边坡稳定等计算，以此来预测河段可能遭受的风险和是否有必要进行后续的水利工程设计，既为水工设计和河道治理工作提供了更便捷精准的方法，同时也为水利安全发展提供技术支撑。

（3）本次模拟计算不足之处在于河道数据偏少且较为集中，上下游连贯性和渭河河道整体性偏差，因此进行空间插值后数据整体性表现不足，关联性较为局部，插值后重新模拟点位较多，该问题可通过增加上下游河道基础数据和减少无关点位两种方法解决。

（4）由于当前设计工作中对高程数据插值处理结果的不准确性已成为亟待解决的问题，本文利用ArcGIS 软件对地理极强的处理能力，通过对河道测量高程数据进行函数插值、转换、空间分析等一系列处理，得到更为直观、连续性好、数据更为密集准确的河道高程数据，因此ArcGIS 软件空间插值方法建议推广在设计工作中使用，不仅提高工作效率，节约大量时间，更重要的是对工程设计和管理工作提供更为精准的数据基础。