基于朴素贝叶斯算法的变权重多目标自适应巡航控制策略
2020-04-29魏洪贵贺伊琳卫龙龙张大禹叶毅铭
魏洪贵 贺伊琳 卫龙龙 张大禹 叶毅铭


摘要:针对目前使用较为广泛的基于模型预测控制的自适应巡航系统,该文提出一种分层控制结构,设计一种变权重的模型预测控制器作为上位控制器。为了获得最佳加速度,综合考虑驾驶员期望车距,车辆自身物理限制,前车加速度影响等因素。使用高斯朴素贝叶斯算法预测前方车辆未来行为,从而采取不同的权重参数策略。通过Matlab/Simulink与Carsim对固定权重参数和可变权重参数分别进行联合仿真,结果表明,随着道路条件的变化,可变权重参数可以提高车辆自适应巡航系统的表现效果,显著降低固定权重策略的系统速度和距离偏差量,有效提高了系统的控制精度与适应性。
关 键 词:自适应巡航控制;模型预测控制;多目标;前车预测
中图分类号:U461.91
DOI:10.16152/j.cnki.xdxbzr.2020-01-004开放科学(资源服务)标识码(OSID):
Strategy of multi-objective adaptive cruise control system withvariable weight based on naive Bayesian algorithm
WEI Honggui, HE Yilin, WEI Longlong, ZHANG Dayu, YE Yiming
(School of Automobile, Chang′an University, Xi′an 710064, China)
Abstract: Aiming at the widely used adaptive cruise control system based on model predictive control, a hierarchical control structure is proposed, which is divided into upper controller and lower controller. A model predictive controller with variable weight is designed as the upper controller. In order to obtain the best acceleration, the expected distance of the driver, the physical limitation of the vehicle itself, the influence of the acceleration of the vehicle in front and other factors are taken into comprehensive consideration.The weight changes according to the future lane changing behavior of vehicles in front of ego vehicle predicted by Gaussian naive Bayesian algorithm. Finally, the fixed weight parameters and variable weight parameters are simulated by Matlab/Simulink and Carsim respectively. The simulation results show that with the change of road conditions, the variable weight parameter can improve the performance of the vehicle adaptive cruise system, significantly reduce the system speed and distance deviation of the fixed weight strategy and effectively improve the control precision and adaptability of the system is improveded effectively.
Key words: adaptive cruise control; model predictive control; multi-objective; forward vehicle prediction
自適应巡航系统(adaptive cruise control,ACC)包括定速巡航和跟车控制,在高速路上车辆较少,自车前方无车情况下,可以开启定速巡航,当前方检测到车辆后则转换为跟车模式,驾驶员无需手动控制车速,可极大地减轻驾驶压力,缓解驾驶疲劳。ACC系统的性能与行车安全性密切相关,因此,研究ACC非常具有现实意义。
近年来,大量学者提出了针对不同情况下的ACC系统解决方案[1]。文献[2-3]针对驾驶员偏好特性,将驾驶风格融合到控制系统中,以提高驾驶员的驾驶适应性。文献[4-5]依靠LTE-V技术使车辆之间可以互相通信,通过协同式控制来保证安全性和舒适性。通过对驾驶模式进行判断并使用对应的控制逻辑,文献[6-7]实现了带有起停功能的全速段ACC系统。文献[8-9]使用可以表征跟车安全性、舒适性、燃油经济性以及追踪性能的目标函数来设计多目标优化ACC系统。另外,使用确定性策略梯度或者DQN的强化学习方法通过训练数据不断改进ACC系统的方法也开始出现[10-11]。这些解决方案使ACC系统可以应用于更广泛的实际道路条件下。但是,这些类型的ACC系统大都集中于对车辆自身以及驾驶员的研究,协同式的ACC系统由于LTE-V技术起步较晚,以及基础设施还不完善等问题还无法商用。
以上系统都没有考虑周围车辆未来的行驶轨迹对自车的影响。本文基于模型预测控制算法设计自适应巡航系统,综合考虑车辆自身以及外部环境干扰等所有影响因素,建立车间纵向运动学模型,通过Matlab/Simulink和Carsim进行联合仿真,探究各个参数对ACC系统的影响规律,使用高斯朴素贝叶斯对前方车辆未来的行为进行预测,对性能指标的权重参数进行调整,使ACC系统取得更加良好的控制效果,满足多目标要求。
1 ACC系统总体设计
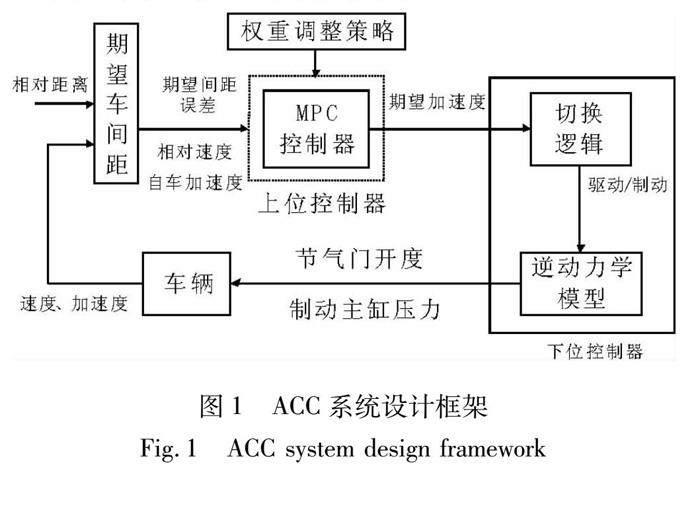
自适应巡航系统的总体设计框架如图1所示。通过传感器检测到自车与前车的相对距离和相对速度,由自车的速度和加速度,计算出前车的速度、加速度、自车期望车间距以及期望车间距误差后,传送到上位控制器模块,由上层控制器MPC根据这些状态量进行计算,再由权重调整策略模块根据周围车辆信息对MPC控制器的权重进行调整,输出期望加速度,将其输入到下层控制器的切换逻辑模块。在汽车行驶的过程中,需要避免同时进行加速和制动的操作,因此,需要设计驱动-制动切换逻辑,其可以通过将期望加速度与在任意滑行速度下,车辆可以获得的最大地面减速度进行比较,来确定车辆应该加速还是减速,接着,经过车辆逆动力学模型得到对应的节气门开度和制动主缸压力,施加于车辆后得到下一个时刻车辆的状态,通过下一个时刻的状态量进行反馈调节,不断地进行滚动优化。
2 上位控制器设计
2.1 车间纵向运动学建模
ACC系统设计主要是对于上层控制器的研究,通过两车间的间距策略来保证行驶的安全性,在此基础上进行优化,来达到舒适性、经济性等多目标要求。两车间的纵向运动学示意图如图2所示,两车间相对距离为dr,跟车期望车间距为ddes,期望车间距误差为de。
ACC系统关键技术之一是对间距策略的研究,以满足行车安全性、舒适性、经济性及动态性,本文采用文献[12]中的固定车头时距策略的期望车间距计算方法:
ddes=thv+d0。(1)
其中:th為固定车头时距;v为自车速度;d0为最小固定车间距,本文取4 m。
由于车辆自身动力传递结构的原因,车辆无法立即达到给定的期望加速度,即车辆达到期望加速度存在一定的滞后性。期望加速度ades经下层控制器作用于车辆后产生实际加速度a,两者之间的关系可以用一阶惯性环节表示[13],
a=Kτs+1ades。(2)
其中:K为一阶惯性系统增益;τ为一阶惯性系统时滞。
选取期望车间距误差de、相对速度vr与自车加速度a作为系统状态向量:
x=[de, vr, a]T, (3)
结合车间纵向运动学模型,可得如下状态方程:
=Ax+Bu+Gw,
y=Cx。(4)
其中:控制输入u为自车加速度,系统干扰量w为前车加速度,各系数为
A=01-th
00-1
00-1τ, B=001τ
,
G=010, C=100
010
001
为了后面使用控制增量计算,构造一个新的状态量如式(5)所示,
ξ(k|t)=x(k|t)
u(k-1|t)
。(5)
则新的状态方程为
ξ(k+1|t)=ξ(k|t)+ΔU(k|t),
η(k|t)=ξ(k|t)。(6)
其中:
=AB
0m*nIm
; =B
Im
; =[C 0]。
将预测时域内的输出量和控制时域内的控制增量分别表示成向量形式,即
Y(t)=η(t+1|t)
η(t+2|t)
η(t+p|t)
,
ΔU=Δu(t|t)
Δu(t+1|t)
Δu(t+c|t)
,(7)
其中:p为预测时域;c为控制时域。
则向量形式的状态方程为
Y(t)=ξ(t|t)+ΔU(t)。(8)
其中:
=
2
p
;
=00…0
0…0
p-1p-2……p-c-1
。
在给定当前时刻的状态量和控制增量下,可以通过式(8)计算出预测时域内的一系列状态量和状态增量,从而实现系统的预测功能。
2.2 基于MPC的多目标控制算法
基于所建立的预测方程,本节通过设定目标函数求解最优控制增量。目标函数需要满足安全性,舒适性,经济性和动态性。
安全性可以由跟车间距得到,使汽车满足
dr≥ds=max(tTTCΔv,d0)。(9)
其中:ds为安全距离;tTTC为碰撞时间(time to collision, TTC),表示两车保持当前速度下发生碰撞所需的时间[14]。
为使车辆具有快速跟踪前车的速度并达到期望跟车间距的能力,可以对期望跟车间距误差以及相对速度最小化[15],以满足ACC系统动态性的要求。
Ja=q1Δd2+q2Δv2。(10)
其中:q1,q2 是权重系数。
考虑经济性的目标,由文献[16]可知,系统的动态响应曲线越平滑,就越有利于经济性的提高,可以通过加速度描述其平滑性,间接表征经济性,
Jb=q3a2。(11)
研究表明,乘坐的舒适性可以通过加速度变化率j来表示[17],即
Jc=q4j2。(12)
由此可得,设计的目标函数如下
J=∑(Ja+Jb+Jc)=
∑Npi=1‖η(k+i|t)-ηref(k+i|t)‖2Q+
∑Nc-1i=1‖ΔU(k+i|t)‖2R,(13)
Δdmin≤Δd(k)≤Δdmax,
Δvmin≤Δv(k)≤Δvmax,
amin≤a(k)≤amax,
jmin≤j(k)≤jmax,
umin≤u(k)≤umax。(14)
其中,Q,R为权重对角矩阵。
3 基于前方车辆行为预测的权重调整策略
3.1 高斯型朴素贝叶斯算法
朴素贝叶斯是一种常用的分类算法[18],相对于其他机器学习算法,朴素贝叶斯可以在仅有少量的训练数据下得到估计分类所需的参数。因此,本文采用朴素贝叶斯对前车行为预测进行研究。
贝叶斯算法如式(15)所示
p(c|x)=p(x|c)p(c)p(x)。(15)
其中,p(c|x)为在特征x的条件下前车行为是c的概率,p(x|c)为在前车行为是c条件下前车特征为x的概率。
由于朴素贝叶斯假定特征之间是独立同分布,对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,以概率最大的类别作为待分类项所属类别,本文采用朴素贝叶斯算法表示形式如下
y=argmax
p(Y=ck)∏kj=1p(X(j)=x(j)|Y=ck)∑ki=1p(Y=ci)∏kj=1p(X(j)=x(j)|Y=ck) 。(16)
考虑到车辆的坐标是随着时间变化的,是一个连续值,所以,本文采用高斯型朴素贝叶斯算法。将车辆的行为分为3种:向左换道,车道保持,向右換道,即Y={向左换道,车道保持,向右换道}。
通过传感器获取到周围车辆坐标位置后,选择4个特征X={s, d, , }。特征s,d 分别为车辆在Frenet坐标系下的纵向坐标和相对道路中心线的横向偏移量。特征, 为纵向速度和横向速度。假设4个特征量之间相互独立,并且符合高斯分布,即
p(x|c)=12πσe-(x-μ)22σ2。(17)
其中:μ为特征的平均值;σ2为特征的方差。
3.2 权重调整策略
当使用高斯型朴素贝叶斯预测出本车道以及邻车道的前方车辆行为后,如果满足系统设定的规则,则调整权重参数以适应道路变化情况。
对于设定的规则,本文分为两种情况考虑,一是当本车道前方车辆变道,切出本车道后,自车的跟踪目标变为本车道上更远的前方车辆;二是当左右邻车道前方车辆切入本车道后,自车跟踪目标变为新切入的车辆。两种情况下都应该调整权重参数。
通过文献[19]可知,当q1> q2时,系统更加重视对于距离误差的消除,控制器必须在极端输入值,即最大和最小自车加速度之间进行频繁切换以保持距离误差最小化,因此,输入中存在大量振荡;而当q1 < q2时,控制器更加保守,达到所需的终端状态需要更长的时间,但输入更加稳定。当q1和q2都很大时,系统消除间距和速度误差的响应会非常迅速,但会引起控制误差的增大,使系统稳定性降低。因此,需对q3进行选择以达到响应时间与控制精度的平衡。而q4的权重系数较小,故本文仅对前3个权重系数进行调整,q4作为固定权重系数,取0.01。
在驾驶期间,针对不同的道路情况,对系统的响应速度要求也会不同。某些情况下,要求系统作出快速响应,则需要增大q1, q2。而在另外一些情况下要求优先保证驾驶体验,则可以考虑增大q3。
本文针对前方车辆驶离主车所在车道以及其他车道上车辆切入主车车道两种情况设置了不同的系统权重参数,以满足车辆系统的不同需求。
当前方车辆驶离主车所在车道时,前车变道一般是由于其前方车辆的车速较低,因此,前车换道后,主车与新跟踪目标车辆的距离大于期望间距,Δd为正值,但是相对速度变小,Δv为负值,此时可以平稳地进行减速,因此q2和q3应较大,q1较小,即参数调整为 (q1-, q2+, q3+)。
当其他车道上车辆切入主车车道时,会先降低车速后再转入当前车道,接着迅速提升速度,所以,主车与新跟踪目标车辆的距离小于期望间距,相对速度也变小,由于Δd和Δv均为负值,应该尽快减速,因此q1和q2应较大,q3相对较低,以避免碰撞,即参数调整为 (q1+, q2+, q3-)。
本文对于另一种场景,即其他车道上车辆切入主车车道时候为加速情况,Δd为负值,Δv为正值,可以考虑使用较小的速度权重q2-,但为了行车安全性,还是采用q2+权重。即不管其他车道上车辆是加速切入主车车道还是减速切入主车车道,都采用 (q1-, q2+, q3+)。权重调整策略流程如图3所示。
4 仿真与结果分析
为了验证本文所提算法的正确性,采用Matlab和Carsim进行联合仿真试验,对固定权重和变权重多目标ACC系统进行对比,仿真场景在Carsim软件环境下搭建,算法在Matlab中运行,将Carsim输出的自车状态参数以及周围车辆的位置参数输入到Matlab中进行计算,再将计算得到的节气门开度和制动主缸压力输送回Carsim中,形成闭环系统。仿真平台结构如图4所示。仿真车辆模型是以Carsim中CS B-Class的Hatchback为基础模型进行改进,设定车辆参数,轴距为2.77 m,其对应的原型是现实中ACC功能装备率较高的B级车这一级别的车型,根据文献[20] 设定Carsim中的相关参数。MPC控制器关键参数是根据参考文献[21]中高速ACC的Q矩阵设置了基础的q1,q2,q3。其余参数设置是根据参考文献[22]以及仿真试验效果所得。
Carsim相關参数如表1所示,MPC控制器关键参数设置如表2所示。
本文模拟了两种不同的场景,其中自车一直保持在本车道上,但由于前方车辆的不同行为,为满足多目标要求而对自车做出相应的调整。仿真设定的场景是在同方向上有3条以上车道的高速道路上,考虑到交通法规要求的高速道路最低限速以及驾驶员通常在道路车流量较小且车速较快的条件下开启ACC功能,因此,选择符合日常驾驶场景的30 m/s和28 m/s的初速度设定。
场景1:前车切出车道
场景1假设主车以30 m/s的速度行驶。由于前车正驶向旁边车道,在主车前方62 m处检测到一辆速度为20 m/s的新前车。根据式(1)得到期望间距误差Δd=7 m,相对速度Δv=-10 m/s,因此,在这种情况下需要平稳减速,调整加权参数的值为 (q1-, q2+, q3+)。由图5(a)可以看出,在时间t=4.0 s之前,固定权重和变权重ACC控制策略与前车的间距近乎相同,处于快速跟随期望间距阶段,在时间t=4.0 s之后, 固定权重ACC下自车与前车的实际间距和期望间距的最大差值为6.5 m, 而变权重ACC最大差值仅为 2.3 m, 最大间距差降低了64.6%。 图5(b)和5(c)中,在时间t=2.8 s之前,固定权重和变权重ACC控制策略的速度、加速度基本一致,在t=2.8 s时,变权重ACC加速度增大,减缓速度下降,而固定权重ACC在t=3.0 s时加速度才开始增大,在5.9 s时主车速度与前车速度偏差量达到了3.2 m/s,而变权重ACC下车速的偏差量仅为1.2 m/s,最大速度偏差量相对于固定权重策略降低了62.5%。变权重ACC加速度的变化时刻总是早于固定权重ACC,并且变化更为平缓。虽然在保持安全距离的同时,固定权重ACC和变权重ACC最终都能趋于期望跟车间距、前车速度、前车加速度,但变权重ACC收敛地更快,偏差量更小,相对于固定权重ACC,能提前改变车辆状态,趋向于目标曲线,有更好的“预见性”。
场景2:旁道车辆减速后切入车道
当主车以28 m/s的速度行驶时, 旁边车道有车辆切入, 在主车前方45 m处检测到一辆以20 m/s速度行驶的新车辆。因此,Δd=-7 m和Δv=-8 m/s。由于Δd和Δv均为负值,参数调整为 (q1+, q2+, q3-)。图6(a)中,t=4.8 s之前,固定权重和变权重ACC控制策略与前车的间距相差不大,处于快速跟随期望间距阶段,在t=4.8 s之后,固定权重ACC的期望间距最大偏差量达到了4.1 m,变权重ACC的最大偏差量为1.5 m,降低了63.4%。从图6(b)中可以看出,在t=4.3 s之前,固定权重ACC和变权重ACC的速度曲线基本一致,t=4.3 s之后变权重ACC相对于固定权重ACC开始收敛速度加快,固定权重ACC的速度最大偏差量为3.8 m/s,而变权重ACC为2.5 m/s,降低了34.2%。图6(c)中,变权重ACC的加速度变化更为提前,变化幅度小于固定权重ACC。变权重ACC在拐点处总是提前变化,更平缓快速地趋近目标曲线,同样表现出了变权重ACC的“预见性”。
5 结 论
1)针对自适应巡航控制系统,本文考虑前车的不同运动状态,以安全性、舒适性、经济性和动态性为目标,使用模型预测控制算法,设计了一种基于高斯型朴素贝叶斯算法预测前车行为的变权重自适应巡航系统。
2)引入前车加速度作为纵向车间跟驰模型的干扰项,提升系统的控制精度。
3)仿真结果表明,相比固定权重系数ACC系统,本文所设计的ACC系统能对前车行为进行预测并据此调整权重,提前对执行机构进行操纵,平稳地过渡到期望状态,提升了ACC系统的适应性和驾驶乘坐体验。在前车切出场景下,最大速度偏差量和最大距离偏差量分别降低了62.5%和64.6%;在旁车切入场景下,最大速度偏差量和最大距离偏差量分别降低了34.2%和63.4%。
参考文献:
[1] XIAO L Y, GAO F. A comprehensive review of the development of adaptive cruise control systems[J]. Vehicle System Dynamics, 2010, 48(10):1167-1192.
[2] 刘贺. 考虑驾驶员风格的汽车纵向控制策略研究[D].长沙:湖南大学,2018.
[3] BUTAKOV V, IOANNOU P. Driving autopilot with personalization feature for improved safety and comfort[C]∥2015 IEEE 18th International Conference on Intelligent Transportation Systems (ITSC).IEEE, Spain,2015:387-393.
[4] ZHU Y H, ZHAO D B, ZHONG Z G. Adaptive optimal control of heterogeneous CACC system with uncertain dynamics[J].IEEE Transactions on Control Systems Technology,2019,27(4):1772-1779.
[5] 逄吉玲. 协同式自适应巡航控制系统仿真与控制算法研究[D].长春:吉林大学,2018.
[6] NARANJO J E, GONZALEZ C, GARCIA R, et al. ACC+Stop&Go maneuvers with throttle and brake fuzzy control [J]. IEEE Transactions on Intelligent Transportation Systems, 2006,7(2):213-225.
[7] YAMAMURA Y, TABE M, KANEHIRA M, et al. Development of an adaptive cruise control system with stop-and-go capability[C]∥SAE 2001 World Congress,2001.
[8] EBEN LI S, LI K Q, WANG J Q. Economy-oriented vehicle adaptive cruise control with coordinating multiple objectives function[J]. Vehicle System Dynamics, 2013, 51(1):1-17.
[9] GUO L, GE P S, QIAO Y F, et al. Multi-objective adaptive cruise control strategy based on variable time headway [C]∥2018 IEEE Intelligent Vehicles Symposium (IV).IEEE, Changshu, 2018:203-208.
[10]DESJARDINS C, CHAIB-DRAA B. Cooperative adaptive cruise control: A reinforcement learning approach[J].IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4):1248-1260.
[11]LI Z J, CHU T S, KOLMANOVSKY I V, et al. Training drift counteraction optimal control policies using reinforcement learning: An adaptive cruise control example[J].IEEE Transactions on Intelligent Transportation Systems, 2018,19(9):2903-2912.
[12]YI K. Vehicle-to-vehicle distance and speed control using an electronic-vacuum booster[J]. JSAE Review,2001,22(4):403-412.
[13]ZHU M, CHEN H Y, XIONG G M. A model predictive speed tracking control approach for autonomous ground vehicles[J]. Mechanical Systems and Signal Processing,2017,87:138-152.
[14]MINDERHOUD M M, BOVY P H L. Extended time-to-collision measures for road traffic safety assessment[J]. Accident Analysis and Prevention,2001,33(1):89-97.
[15]BAGESHWAR V L, GARRARD W L, RAJAMANI R. Model predictive control of transitional maneuvers for adaptive cruise control vehicles [J]. IEEE Transactions on Vehicular Technology, 2004,53(5):1573-1585.
[16]ZHANG J, IOANNOU P. Longitudinal control of heavy trucks in mixed traffic: Environmental and fuel economy considerations[J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(1): 92-104.
[17]YI K, CHUNG J. Nonlinear brake control for vehicle CW/CA systems[J].ASME Transactions on Mechatronics, 2001,6(1):17-25.
[18]李航.统计学习方法[M].北京:清华大学出版社,2012.
[19]ZHAO R C, WONG P K, XIE Z C, et al. Real-time weighted multi-objective model predictive controller for adaptive cruise control systems[J].International Journal of Automotive Technology,2017,18(2):279-292.
[20]熊坚,王秀圣,刘丁.汽车ACC 系统算法仿真研究[J].重庆交通大学学报(自然科学版),2017,36(9):108-114.
XIONG J, WANG X S, LIU D. Simulation of vehicle ACC system algorithm[J].Journal of Chongqing Jiaotong University(Natural Science), 2017, 36(9):108-114.
[21]陆逸适,张哲,王立强,等.带启停巡航功能的全速自适应巡航控制器的设计[J].机械设计与制造,2017(5):174-177.
LU Y S, ZHANG Z, WANG L Q, et al. Design of vehicle full-speed adaptive cruise control with stop and go[J].Machinery Design & Manufacture, 2017(5):174-177.
[22]罗莉华.车辆自適应巡航系统的控制策略研究[M].上海:上海交通大学出版社,2013.
(编 辑 李 静)
