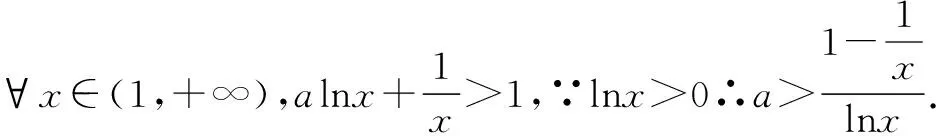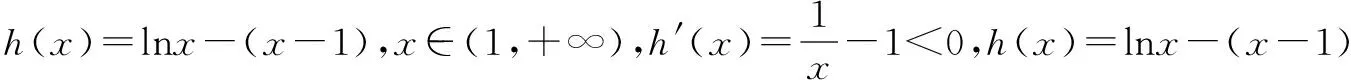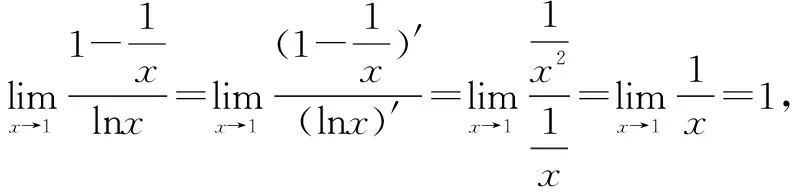新课标下的高中数学微课题研究
———不等式恒成立问题的解题策略
2020-04-29成亮
成 亮
(江苏省南京市宁海中学 210024)
研究背景微课题研究是一种当下热门的数学问题的研究形式,恰逢新课程标准的颁布,不禁让笔者思考:新课标下哪些内容可以设计成微课,最终能否形成符合新课标的校本微课程?笔者所教的是一所省重点高中的高二年级理科班,在学习了导数这一章后,通过智学网进行了一次单元测试,测试结果如图:
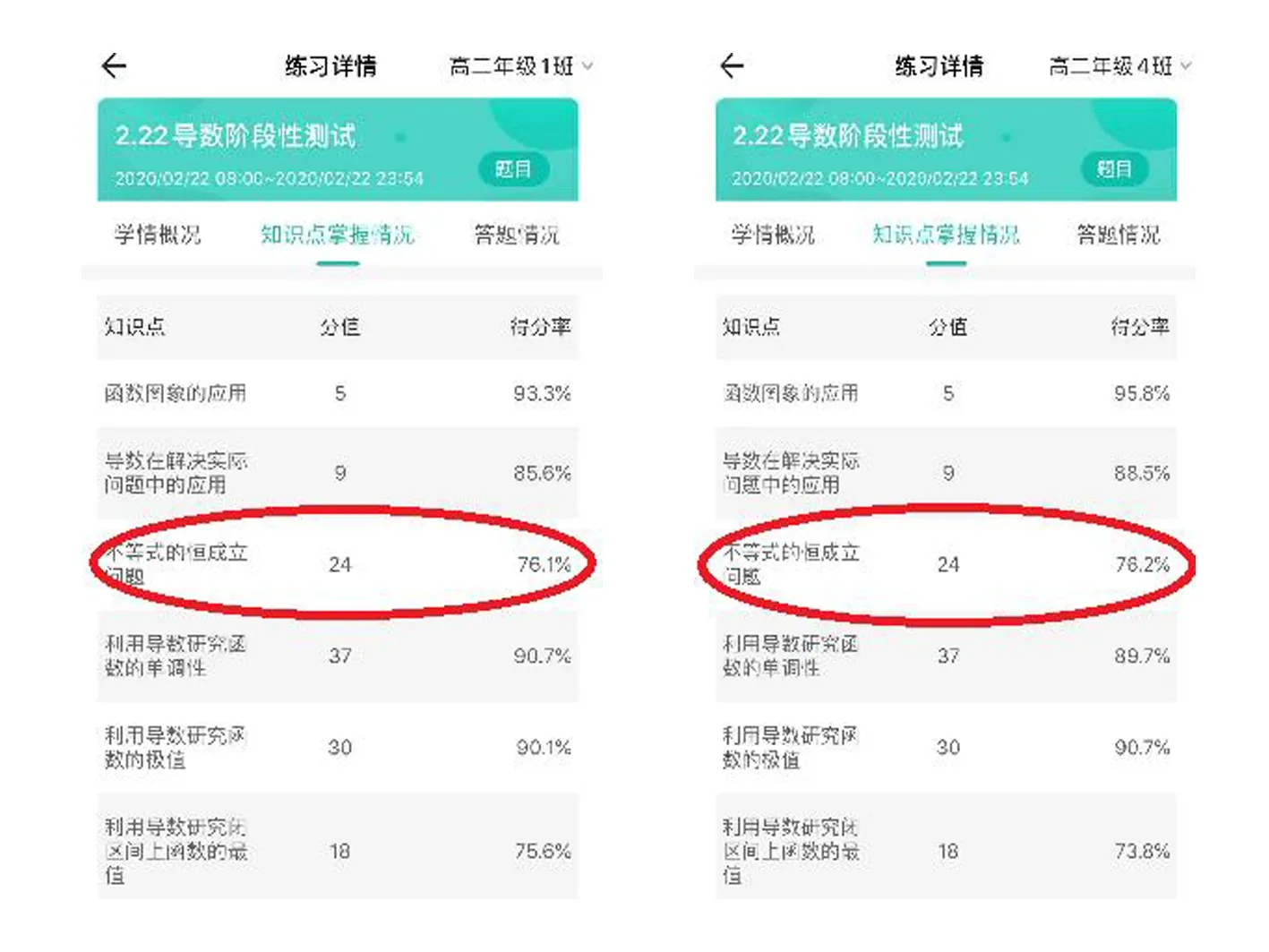
可以看出,正确率低于百分之八十的问题就有不等式恒成立,为了突破此难点问题,笔者设计了一节微课,录制成一节微课视频,让学生通过30分钟自主学习,最后15分钟进行同题型智学网当堂检测.
一、参变量分离解决不等式恒成立问题
参变量分离,即将不等式进行等价变形,将参数与变量完全分离开来,形成以下四种形式之一:
①∀x∈A,t≥f(x);②∀x∈A,t>f(x);③∀x∈A,t≤f(x);④∀x∈A,t 例1若不等式lnx≤tx,对∀x∈(0,+∞)恒成立,则t的范围为____. 分析此题是不等式恒成立问题,首先采取参变量分离解决. 当不等式能够参变量分离时,参变量分离是解决不等式恒成立问题的首选方法. 当不等式中参数与变量没办法完全分离时,我们往往需要转变思路去构建含参的函数,形式如下:∀x∈A,f(x)>0或∀x∈A,f(x)≥0,其中f(x)是含参的函数,对参数分类讨论,只要f(x)min>0或f(x)min≥0即可. 例2若不等式x-t2≥tlnx,对∀x∈[1,+∞)恒成立,则t的范围为____. 分析此题参数t与变量x不能够完全分离开来,故将不等式移项x-t2-tlnx≥0,构建含参数t的函数f(x),对t进行分类讨论,使得f(x)min≥0即可 (1)当t≤1时,f′(x)>0,则f(x)在x∈[1,+∞)上单调递增,f(x)min=f(1)=1-t2≥0,所以t∈[-1,1]. (2)当t>1时,当x∈(1,t),f′(x)<0,f(x)在(1,t)上单减,当x∈(t,+∞),f′(x)>0,f(x)在(t,+∞)上单增,f(x)min=f(t)=t-t2-tlnt<0与题意矛盾. 综上t∈[-1,1] 分析此题时不等式恒成立问题,首先考虑参变量分离,不妨试一下. 处理方法一 :用洛必达法则求极限 处理方法二 :转变思路构建含参的函数进行分类讨论求最值 综上:a≥1. 本节课在学生学完后随即用以下四道选择题进行了学习效果的检测: 1.已知不等式ex≥ax对任意的x∈[0,+∞)恒成立,则a的取值范围为( ). A.(-∞,e) B.(-∞,e] C. (-∞,1) D.(-∞,1] A.[2,+∞) B.(-∞,2] C. (2,+∞) D.[2,+∞) 4.函数f(x)=a(x2-1)-lnx,若f(x)≥0对任意x∈[1,+∞)恒成立,则a的取值范围为( ). A.[0,+∞) B.[1,+∞) 这四道题题型与单元测试一样,其中第1,2,3三题难度与单元测试中的题难度系数相当,第4题比单元测试中难度要大很多,在此前提下得如下结果: 从此图可以看出经过半小时的微课学习,正确率有所提升,由于微课学生课后还可以反复观看学习,相信正确率的百分比会提高更多.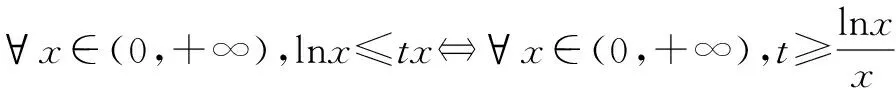
二、构建含参函数解决不等式恒成立问题
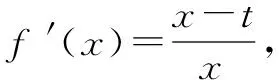
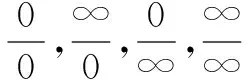
三、能参变量分离,但最值处无意义时的两种处理方法