高中数学立体几何教学策略探寻

杨文娟

(江苏省徐州市郑集高级中学 221100)

在立体几何知识教学中，我们发现，部分学生要么基础知识掌握不牢固，要么未掌握相关的解题技巧，导致在解题中的出错率较高，因此立体几何教学中，应做好教学策略的探寻与总结，结合具体内容加以积极应用，使学生深入理解立体几何知识，掌握相关的解题技巧，不断提高解题水平.

一、优化教法，提升体验

高中数学立体几何教学中，部分学生的空间想象能力较差，学习效率低下.因此应注重教学方法的创新，帮助其在头脑中建立清晰的空间模型，降低学习难度，提升学习体验，树立学习立体几何知识的自信心.一方面，结合教学内容，鼓励学生制作相关的模型，包括正方体、长方体、棱柱、棱锥，鼓励其从不同角度观察这些模型，了解模型中点线面的构成.另一方面，充分利用多媒体技术制作相关的教学课件.在课堂上借助大屏幕将空间几何图形直观、形象地展示给学生，并尝试着提出一些问题供学生思考，使其更加深刻地理解点线面的关系.

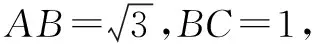
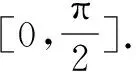
二、鼓励总结，整合所学

众所周知，高中数学立体几何涉及较多的概念以及解题方法，为提高学生解答立体几何试题的效率，应鼓励及注重总结，整合所学，能够迅速地从已知条件中寻找解题的思路，避免走进解题误区.一方面，鼓励学生总结立体几何中常见的问题，如证明线面垂直、面面垂直、求解两面角，以及求解点到面的距离.思考解答这些问题时应用的知识点，并加以认真的汇总，形成明确的解题思路.另一方面，鼓励学生总结解答立体几何问题的方法.一般情况下解答立体几何题目有两种思路：其一，应用立体几何思路求解；其二，应用向量知识求解.解题中要求学生具体问题具体分析，根据题设条件灵活应用，及时找到解题突破口.

例2如图1，几何体是圆柱的一部分，它是由矩形ABCD(及其内部)以AB边所在的直线为旋转轴，旋转120°得到，其中G是弧DF的中点.

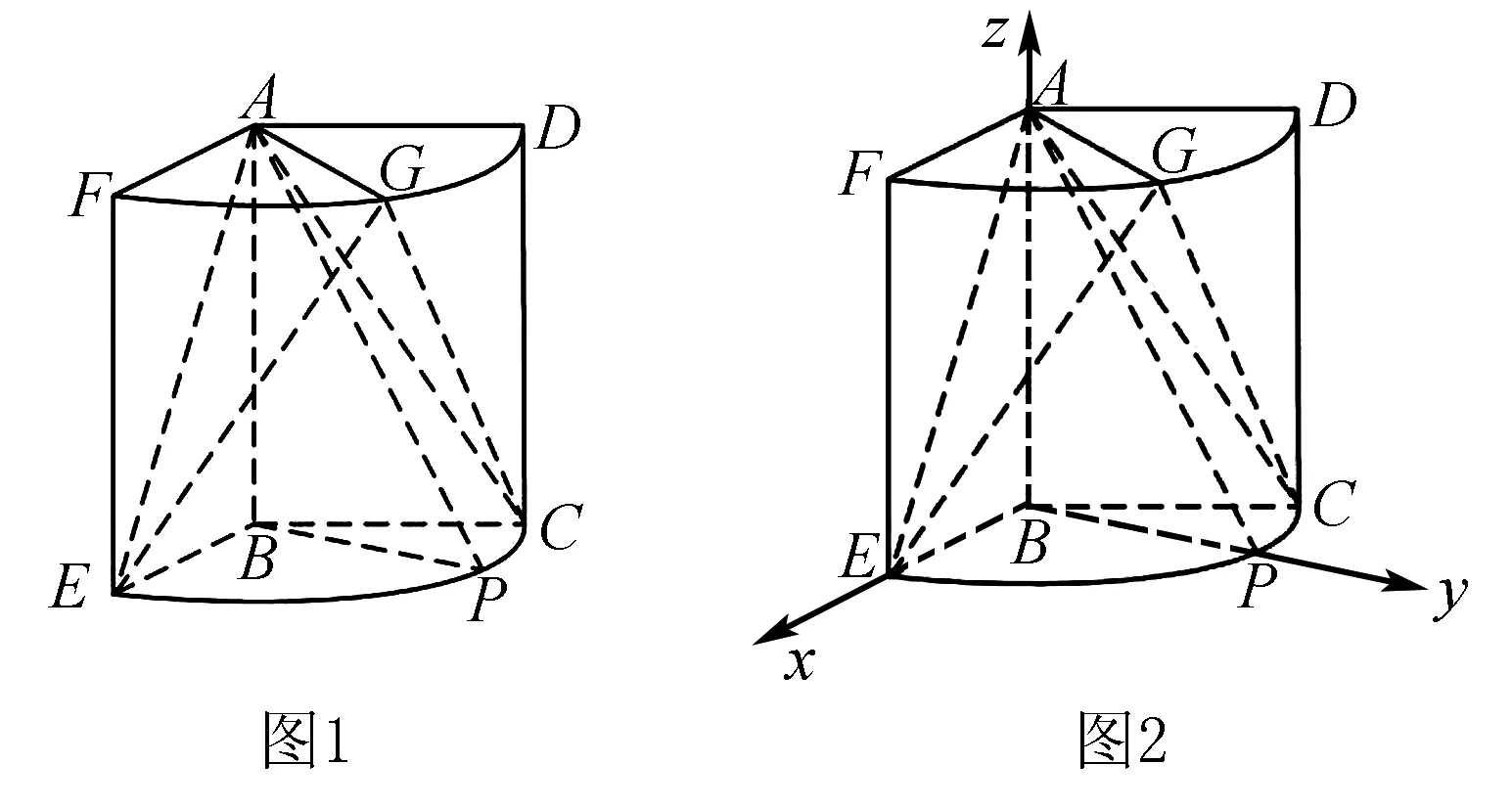
(1)设P为弧CE上的一点，且AP⊥BE，求∠CBP的大小；(2)当AB=3，AD=2，求二面角E-AG-C的大小.

三、注重训练，传授技巧

高中数学立体几何教学中，提高学生的学习能力尤为重要，通过训练可明显提高学生的学习能力，因此授课中应严把训练关，提高训练质量.一方面，做好高考中立体几何试题的汇总与分析，选择优秀的训练题目，要求学生积极思考，认真作答，及时弥补在训练中暴露的薄弱点，堵住立体几何知识漏洞.另外，在训练中为拓展学生思维，选择或创设较为新颖的立体几何问题，不断提高学生分析解答立体几何试题能力.另一方面，传授立体几何问题解答技巧，在解答立体几何问题时可根据实际情况灵活运用解题方法，如采用特例法来大大简化计算，提高解题正确率.

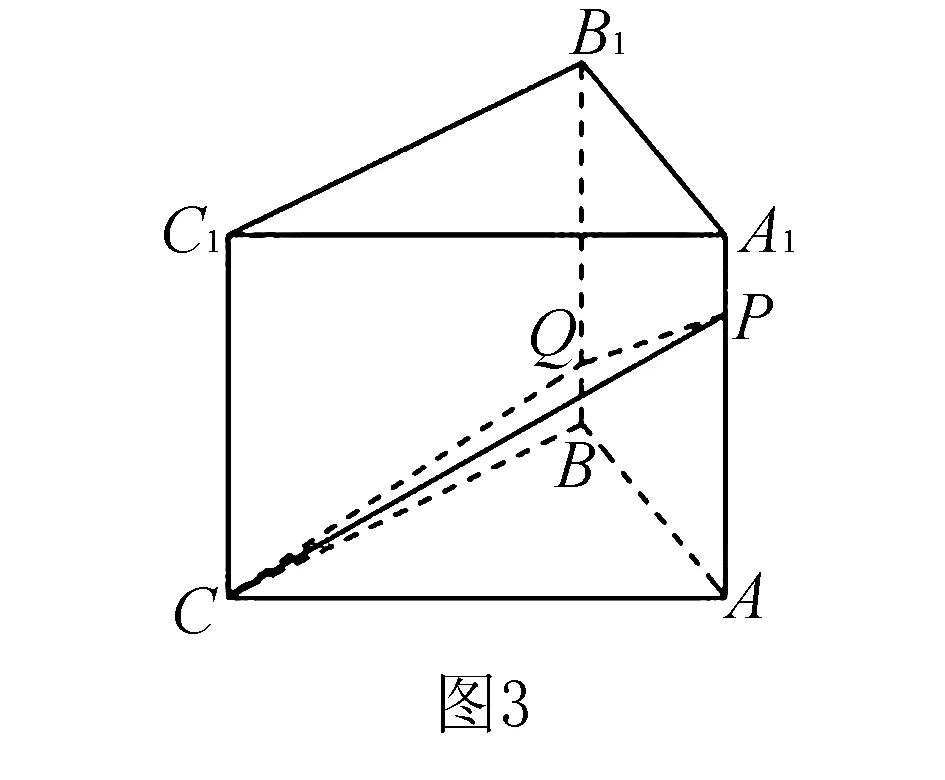
例3如图3，在三棱柱的侧棱A1A和B1B上各有一动点P、Q且A1P=BQ，过P、Q、C三点的截面，把棱柱分为上、下两部分，则上下两部分的体积之比为____.

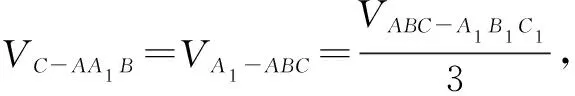
综上所述，高中数学立体几何教学中为获得预期的教学目标，应积极探寻相关教学策略，并积极应用于教学实践中，结合教学效果，对教学策略进行针对性的优化，总结一套适合自己的教学方法，使学生在夯实立体几何基础知识的同时，学习能力得以明显提升.