试论核心素养下的高中数学教学策略
2020-04-29赵蕾
赵 蕾
(江苏省白蒲高级中学 226511 )
高中数学课程标准从六个方面对核心素养内容进行详细阐述.为保证核心素养内容的认真落实,应认真分析其内涵,找到与高中数学知识的契合点,将核心素养培养工作与高中数学教学工作有机地融合在一起,提高高中数学教学效率的同时,认真开展核心素养培养工作,使学习者能够终身受益.文章从数学抽象、逻辑推理、数学建模、直观想象素养入手,探讨相关教学策略.
一、注重启发,培养数学抽象素养
数学抽象素养是学习及应用数学知识解答相关问题的重要素养,为提高学习者的数学素养,授课中应加强理论知识学习,提高数学抽象素养培养意识.一方面,讲解数学知识时,启发学习者自己进行抽象、总结,概括相关数学结论,使其参与到数学知识的形成过程,加深对数学知识的印象.另一方面,尝试着设置一些有趣的数学抽象问题,鼓励学习者进行思考,尤其应注重给予学习者启发,使其找到抽象的突破口,降低抽象的难度,增强其学习的自信.
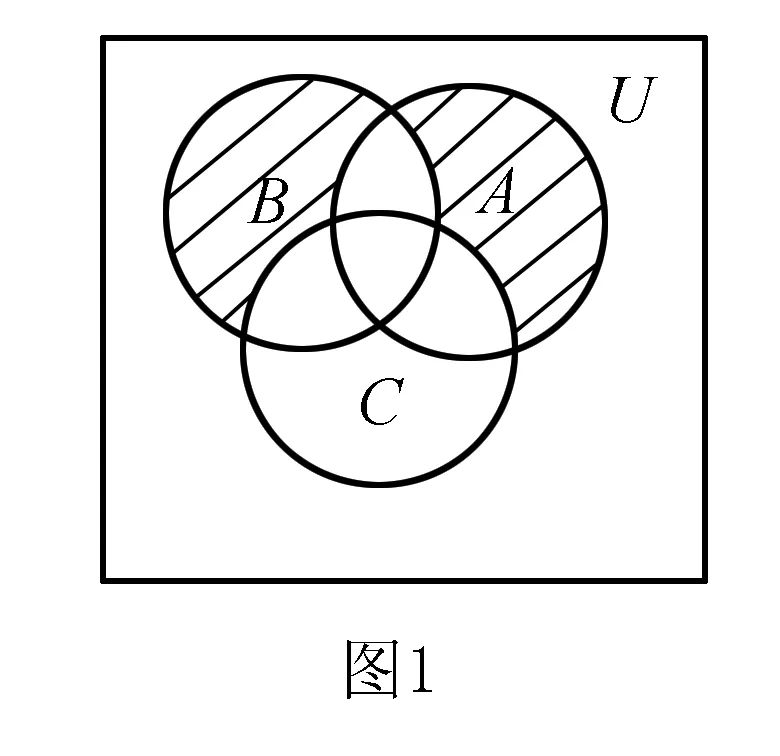
例1如图1所示,已知集合A、B、C为全集U的子集,则图中阴影部分所表示的集合为____.
从图形与图形关系中,抽象图数学概念与概念之间的关系,并用数学语言予以表证,属于数学抽象素养的范畴.该题目要求认真观察图形,使用集合语言意义表征,可很好的培养学习者的数学抽象素养.解题中给予学习者启发,要求其认真回顾集合及补集知识.认真分析可知,阴影部分表示的集合,可表示为:{A∩[U(B∪C)]}∪{B∩[U(A∪C)]}.通过该题目的讲解,使学习者意识到,解答相关数学试题时,应认真联系所学,不断提高数学抽象素养的提升.
二、营造氛围,培养逻辑推理素养
逻辑推理素养是学习数学知识的基本素养,与学习者学习成绩的提升关系密切,因此授课中应将逻辑推理素养培养纳入授课的重点.一方面,不仅要讲解逻辑推理相关知识,而且在课堂上积极营造宽松活泼氛围,鼓励学习者相互讨论、合理推理,使其亲身感受推理过程,明确推理注意问题,掌握相关的推理方法.另一方面,定期开展逻辑推理比赛活动,充分调动学习者的逻辑推理热情,提高学习者推理思维的灵活性,更加深入地掌握不同问题情境下的推理类型,保证推理的严谨性与科学性.
例2若2.5x=1000,0.25y=1000,则1/x-1/y=____.
该题目灵活考查学习者对数函数掌握与灵活应用情况.解题中需应用对数相关运算,进行合理推理,对学习者的思维能力要求较高.由已知条件不难得出,x=log2.51000,y=log0.251000,1/x=1/log2.51000=log10002.5,同理,1/y=log10000.25,则1/x-1/y=log10002.5-log10002.5=log100010=lg10/lg1000=1/3.通过该题目的讲解,使学习者认识到,为保证逻辑推理的正确性与合理性,认真学习数学基础知识,做到深入理解是推理的基础.
三、创设情境,培养数学建模素养
数学建模是应用数学知识解答问题的重要一环,为提高学习者的数学建模素养,教学中应注重落实以下内容:一方面,通过讲解数学建模知识,引导学习者重视高中数学中的常见模型,明确数学建模的步骤以及方法,认真把握各种模型构建过程中的细节,保证建模的正确性.另一方面,围绕所学的数学知识,注重创设相关问题情境,锻炼学习者的数学建模能力.建模过程中要求学习者认真分析,提取有效信息,明确相关参数范围,构建对应数学模型.
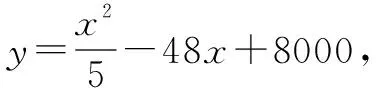
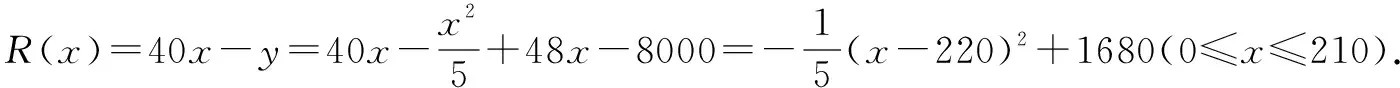
四、加强鼓励,培养直观想象素养
直观想象素养不仅有助于学习者更加深刻地认识几何图形,而且能提高相关问题解题能力,因此,应围绕高中数学相关知识,做好直观想象素养培养工作.一方面,鼓励学习者做一个有心之人,尝试着绘制生活中常见的空间几何图形,培养学习者的抽象思维能力,加深对几何图形的深入理解与认识.另一方面,明确高中数学几何知识教学重点,积极创设新颖、动态的问题情景,鼓励学习者积极回顾所学,构建“数”与“形”之间的对应关系,加以成功解答.
例4 已知正方体ABCD-A1B1C1D1的棱长6,M是BC的中点,点P是侧面DCC1D1所在平面内的动点,且满足∠APD=∠MPC,则三棱锥P-BCD的体积最大值是____.
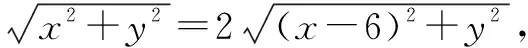
综上所述,高中数学核心素养培养是一个系统性工作,应提高认识,系统学习核心素养相关内容,储备丰富的理论知识,为更好地渗透于高中数学教学之中奠定基础.本文通过讨论认为,为提高核心素养下高中数学教学质量与水平,认真研究核心素养内容与数学知识的对应关系,通过教学启发、营造氛围、创设情景、加强鼓励等措施,结合具体教学内容与相关习题,认真践行核心素养培养工作.
