基于多模光纤的高分辨率光谱仪

田德明，王艳红，武京治

(中北大学 信息与通信工程学院，山西 太原 030051)

0 引 言

光谱仪已经被广泛应用于生物传感、 材料分析和光源特性分析等各个领域[1]. 现有的光谱仪大多采用光栅、 棱镜或者利用光的干涉来分散光波，光谱分辨率与光路的长度成比例. 因此，光谱仪想要满足分辨率和体积的需求只能在这两者之间进行权衡. 高分辨率的光谱仪由于其体积大，价格高昂，因此仪器设备只能出现在实验室中[2]. 同时，传统光谱仪是基于一维的光谱到空间映射，但是近几年耶鲁大学应用物理系的Brandon Redding等人通过对无序光子晶体、 随机散射介质和布拉格光纤阵列等器件的研究发现，可以使用二维的光谱到空间来得到光谱. 虽然这种方法比传统的光栅或棱镜更为复杂，但它为选择色散元件提供了更大的灵活性. 由于光纤传输的距离长、 损耗小并且多模光纤中不同传输模式之间的干涉使其成为一种理想色散元件. 实现这种二维映射利用的是光在多模光纤中发生干涉后在末端产生的散斑图，过去研究人员通过散斑图对比度来测量激光的线宽，与之前的使用统计特性不同，本文提出了通过记录不同波长的整个散斑图中包含的空间强度信息来恢复未知光谱. 此外，与传统光谱仪相比，可以克服仪器体积与分辨率之间取舍的问题，光纤可以卷成一个小体积. 同时，光纤光谱仪成本极低，是商业光谱仪的几十到几百分之一，却能够提供与最先进的光栅光谱仪竞争的光谱分辨率.

1 光谱仪的原理与结构

1.1 散斑图的形成原理

大芯经光纤可以支持数千种空间模式. 散斑图案正是由于光在传输过程中这些模式之间的干涉产生的. 多模光纤的各个参数都会影响散斑图的空间光强分布，进而影响光谱仪的性能，例如，光纤长度L、 芯径W、 数值孔径NA. 由一束单色输入多模光纤中，光纤末端的场分布为可以表示为式(1)[3].

E(r,θ,λ)=

(1)

式中：E为电场分布;r,θ,λ为坐标变量和入射光的波长;Am和φm为第m个导波模的幅值和初始相位；ψm为模场的空间分布函数；βm为入射波长λ的函数，表示传播常数. 假设多模光纤中的所有模式都被激发，同时初始相位均不相干，随机分布在0～2π上. 波长为λ1，λ2的光源在经过多模光纤后，在光纤末端产生了不同的光场E1和E2，在幅值一定的情况下，散斑图的场分布只与波长相关，因而散斑图样的光强分布差异可以用来识别波长. 采集得到的散斑图如图1 所示.

图1 1 500 nm光波形成的散斑图Fig.1 Speckle pattern formed by 1 500 nm light wave

1.2 多模光纤光谱仪实验验证

实验装置如图2 所示，包括C+L波段可调谐激光器(EMCORE TTX1994 ITLA)、 保偏单模光纤、 多模光纤和InGaAs焦平面红外相机，多模光纤为光谱仪的色散元件，多模光纤末端产生的散斑图的光强分布取决于输入光的波长和偏振态[4]. 为了消除偏振对实验的影响，实验中在多模光纤之前加入了光纤起偏器，使得不同波长的光具有相同的偏振态. 输入光在多模光纤中激发大量的传输模式，不同的模式之间干涉产生不同的散斑图样，散斑图与波长是一一对应的关系，因此提供了输入波长的独特的识别信息，这种识别信息就如同传统光谱仪中的“光谱-空间”映射. 所用的单模光纤和多模光纤的参数如表1 所示.

图2 实验总体设计Fig.2 Overall design of the experiment

表1 光纤参数

(2)

式(2)为干涉散斑图的相关函数[5]，其表征了在某一给定散斑位置两个不同波长的光谱的相关程度. 其中I(λ,x)表示λ波长的光源在光斑x处的光强，然后对不同的λ取平均. 图3 为光谱相关度与波长变化关系图.C(0)/2对应的波长变化值的2倍为光谱仪的最小分辨率，可得，1 m长的光纤光谱仪分辨率为0.108 nm.

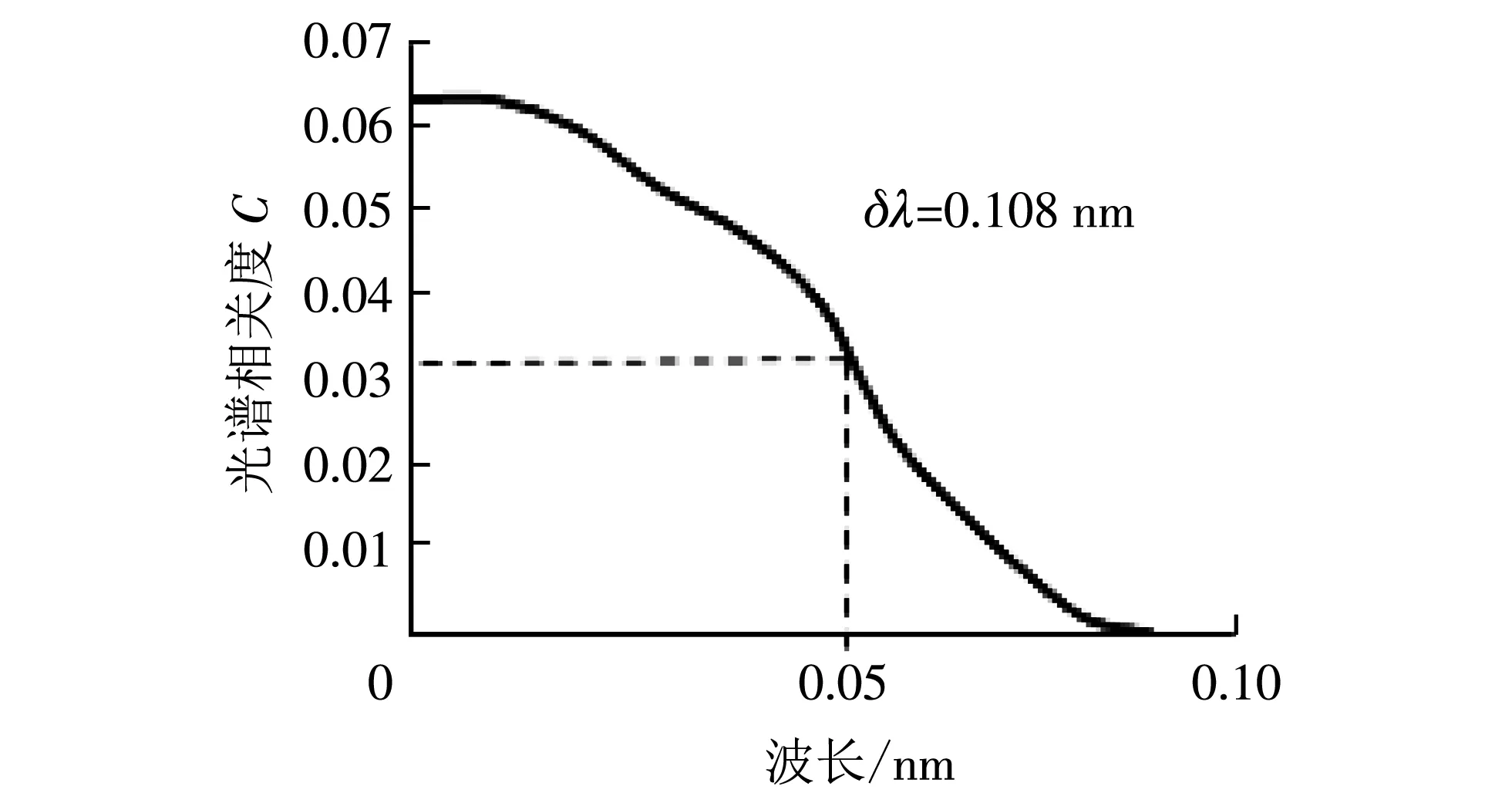
图3 1 500 nm附近光谱相关度随波长变化关系图Fig.3 Spectral correlation and wavelength at 1 500 nm

1.3 偏移熔接对光谱仪的改进

将单模光纤与多模光纤利用FC/APC法兰连接时，多模光纤内激发的传输模式为圆对称高阶本征模，只包含了LP0M模式，数量很少. 此时形成的散斑图相关程度高，不利于提高光谱仪的分辨率. 为了降低散斑图的相关度，在实验中将单模光纤与多模光纤连接时采用偏芯烙接，偏芯熔接结构的两根光纤，由于纤芯失配使得光纤内传输的各个模式在烙点处出现不可预测的随机性变化，激发出大量LPNM模式，这样散斑图的对称性遭到破坏，随机性增强，光斑颗粒尺寸减小，因而携带了更多的信息.

实验得出： 随着偏移量的增加，系统的谱宽基本上成线性减小. 在无噪声情况下，偏移达到12 m时，分辨率最好.

2 光谱恢复算法

2.1 光谱的重建

I=T·S,

(3)

式中：I表示散斑图中采样点的光强；S表示光谱强度； 传递矩阵T储存着每个标定波长对应散斑图的光强的分布信息. 实验的关键之处在于对光谱仪的传递矩阵T的标定. 本文中，将光谱通道从λ=1 499.0 nm 至λ=1 501.5 nm每隔 0.05 nm 进行一次标定，共选取M=51个光谱通道. 采用散斑图上1 296个采样点进行计算，为了求得传输矩阵T的逆矩阵，引入奇异值分解，表示为

T=VDUT,

(4)

D中对角元素Dii=di为正实数，称为传输矩阵的奇异值. 传输矩阵的逆为:T-1=VD′UT. 在校准和光谱恢复的实验中多模光纤的机械不稳定度和光学平台的波动使得散斑图中存在噪声信息，这些值在对对角矩阵D进行倒数运算之后得到了放大，为了消除这种影响，采用截断反演的算法对伪逆矩阵进行优化. 其思想是，设置一个截断值，矩阵D中小于截断值的元素均置零. 于是由截断反演方法得到传输矩阵的逆为T-1tru=VD′truUT. 截断临界值为矩阵D中元素最大值的百分系数.

图4 为光谱的恢复误差与选取不同截断值的关系图，截断值的最优值为0.011 068.

图4 不同的截断值与光谱恢复误差的关系Fig.4 Optical systems with different truncation values and spectral recovery errors

2.2 谱的优化

为了进一步提高光谱准确性，采用非线性的优化算法对光谱进行优化. 遗传算法( GA) 是一种随机全局搜索求最优值的方法，模仿了生物进化方式，其搜索范围广,但不易收敛到最优解的精确值. 模拟退火算法[7]模仿了热力学中，物体逐渐降温到粒子状态最为稳定的物理现象，以求得最优解. 遗传算法加快了算法收敛精度及收敛速度，但增加了陷入局部最优的危险性; 模拟退火算法可以摆脱局部最优但收敛速度慢，容易产生震荡效果. 因此，本文结合两种算法的优点，提出一种改进的遗传模拟退火算法.

遗传模拟退火算法以遗传算法为框架，在执行遗传操作的过程中加入退火操作. 首先对恢复的光谱进行变异操作产生新的解，然后对每个新的解执行退火操作，得到新一代“种群”. 如此循环，直到满足算法结束条件．

这里，将E=‖I-TS‖2看作能量函数. 优化会经过几百上千次的迭代，在每一次的优化过程中，使光谱S中的一个元素随机改变，于是得到一个新的光谱S′，此时计算能量变化 ΔE=‖I-TS′‖2-‖I-TS‖2, exp[-ΔE/T0]为能量E变大的概率，范数为欧几里德范数，T0为初温. 随着迭代次数的增加，温度逐渐降低，能量增加的概率越来越小，当温度低于一定数值时优化结束. 为了对恢复光谱质量进行量化分析，定义光谱的恢复误差为式(5)[8].

(5)

式中：Sreconstructed为光纤光谱仪重建得到的光谱；Sin为光谱的真实值.

最终得到的恢复光谱如图5 所示，通过对比可以看到，直接使用矩阵的逆运算得到的光谱有一定的误差，并且存在噪声信号，通过截断反演方法能够很好地改善恢复光谱的质量. 最终，由遗传-模拟退火算法得到的光谱图与真实值非常接近，误差仅为0.007.

图5 直接恢复和优化后的光谱图Fig.5 Direct recovery and optimization of the spectra

3 光谱仪分辨率和带宽的分析

3.1 光谱重建的验证

由上文得到了长度L=1 m 的多模光纤光谱仪的分辨率为0.109 nm，本文验证1 500.2和1 500.4两个波长光源的重建光谱如图6(a)所示，两条谱线可以很好地分辨出来，而如图6(b)所示，当待测光谱的间隔为0.05 nm小于光纤光谱仪的分辨率之后，待测光谱无法被矩阵的逆运算识别出来. 为了进一步验证光谱仪对任一光谱的重建，展示标定矩阵的波长不包含待测波长的情况，其结果为图6(c)中的重建光谱，虚线为光谱的真实值，实线为测得的光谱，光谱被清晰地分辨出来.

图6 恢复光谱图Fig.6 Recovery spectra

在所有引导模式都被激发的前提下，光谱带宽为Δλ=B*δλ，其中B是光纤支持的引导模式数，δλ是散斑模式的光谱相关宽度[9]. 而引导模式总数B=π2(NA)2W2/2λ2，对于给定的纤芯直径和数值孔径，是固定的，但随着光纤长度的变化是变化的. 较长的光纤能提供更好的光谱分辨率，但带宽更窄. 与传统光谱仪不同的是，单次测量中的光谱覆盖不需要是连续的. 如果已知被测光谱在某些光谱区间内没有分量，则可以将这些区域排除在频谱重建之外，因此有限数量的光谱通道可能获得更宽的光谱范围.

3.2 更高分辨率的验证

为了验证光纤光谱仪具有更高的分辨率，在保证带宽的同时本文选取了长度L=10 m的多模光纤，图7 为其光谱相关曲线，该规格的光纤光谱仪的分辨率为10 pm. 为了验证结果是否准确，这里使用截断反演之后的逆矩阵进行光谱的恢复，之后使用优化算法进行优化.

图7 展示了用该光谱仪获取的光谱图像. 所选取的待测光谱波长为 1 501.001 0 和 1 501.002 5 nm，两条谱线的波长差为15 pm，光纤光谱仪能准确地将这两条谱线分辨出来，可见其具有相当高的光谱分辨率.

4 结 论

本文研究表明，多模光纤可以用作高分辨率的通用光谱仪. 多模光纤中引导模式之间的干涉产生的散斑图案提供了“光谱-空间”的一一对应关系. 与传统的光栅光谱仪相比，在光谱分辨率方面可以提供更好的性能. 多模光纤光谱仪可以通过改变校准的光谱范围来实现与传统光谱仪旋转光栅类似的作用. 当然，光纤光谱仪也有局限性,它需要一个校准步骤，校准后光纤的弯曲程度不能改变. 此外，输入信号的空间分布和偏振必须与校准中使用的相同. 但是，正如本文所展示的，光纤光谱仪利用重建算法可以快速准确地恢复未知光谱，并且尺寸和成本大大降低，可以使一系列新的光谱应用成为可能.