基于EKF的高低温模型修正SOC估算方法

2020-04-29唐淳淳

智能计算机与应用 2020年2期

唐淳淳, 余粟，王盟

(1 上海工程技术大学机械与汽车工程学院，上海 201620； 2 上海工程技术大学工程实训中心，上海 201620；3 上海工程技术大学电子电气工程学院，上海 201620)

0 引言

随着市场的需求、技术的发展加上政府的支持，新能源电动汽车越来越受到大众的欢迎。锂电池因其容量大、功率大、无污染的优点被首选为电动汽车的动力源。锂电池是一个复杂的化学系统，需要电池管理系统(battery management system, BMS)对其进行精确的动态管理。BMS通过对电池的维护与管理，提高续航里程的同时可以给用户带来良好的驾车体验。电池荷电状态(State of Charge, SOC)的估算是电池管理系统(BMS)的基础。由于SOC受充放电电流、电压、温度、放电倍率[1]等诸多因素的影响，对其进行准确估算存在较大困难。

针对上述问题，目前在新能源电动汽车领域，有几种较为经典的SOC估算方法来降低影响。如文献[2]在放电深度及开路电压对应关系基础上建立开路电压法，对电池初末状态的电量估算尤为准确，该方法对端电压要求较高，实际采集过程需要较长时间的静置，给实际应用带来一定难度。文献[3]通过小范围数据建立模型的安时积分法，能实时获得SOC值，但随着循环次数的增加，积累误差明显。文献[4]运用扩展卡尔曼滤波(Extended Kalman Filter, EKF)能一定程度修正安时积分法造成的积累误差，但实际工况下SOC估算的影响因素较多，仍需要通过大量数据进行验算。文献[5]基于神经网络的SOC估算方法拥有较强自我学习能力，很大程度减小了估算误差，但需要大量数据样本的支持，运行复杂。由于现有算法对电池在实际高低温工况下的反应特性考虑甚少，因此针对高低温工况的改进算法具有一定研究意义。

本文针对磷酸铁锂电池在高低温情况下的差异性建立等效电路模型。通过安时积分法，在保证电流采集精度的条件下，由开路电压法获得初始SOC，结合EKF鲁棒性较强的优点对误差进行修正，提出了基于EKF的高低温模型修正SOC估算方法，进一步减小了高低温对电池容量保持量产生的估算误差。

1 等效电路模型的建立及参数辨识

到目前为止，学界已经研发出了Rint模型、Thevenin模型、PNGV模型等。其中，Rint模型为最早提出的一阶模型，适用于线性关系简单明显的单体电池及电池组。Thevenin模型阶数较少，考虑了电池内部的极化电阻影响，但由于模型参数准确度不高，累积误差严重。PNGV模型为典型的非线性模型，不适合长时间仿真，累积电压影响实验精度。

1.1 等效电路模型的建立

本文在Thevenin模型的基础上新增一个极化电路的RC回路，如图1所示。R1C1代表电化学极化反应，R2C2代表浓差极化反应，UOC表示开路电压，R0为电池内部的欧姆内阻，V(t)表示电池的端电压。该二阶RC电路细化了电池的极化特性，较好地表征了电池电压的回弹特性。当电路闭合处于放电状态时，等效电路中电流方向与图2中方向一致。

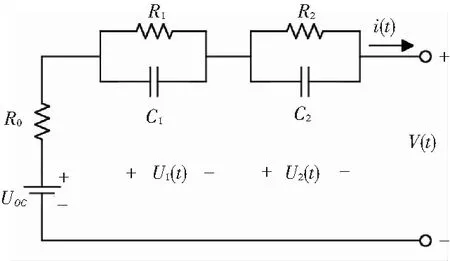
图1 二阶RC 等效电路模型

根据二阶RC等效电路模型，结合基尔霍夫定理推导出其模型状态方程如下所示：

V(t)=UOC(t)-R0i(t)-U1(t)-U2(t),

(1)

(2)

(3)

结合图1的等效电路模型，由于锂电池的放电过程是一个非线性的过程，可将式(1)中的UOC(t)通过SOC与OCV的非线性对应函数f(SOC)来表示。研究选用多项式函数，因为这种函数在微机上的计算效率比对数函数以及指数函数都要高。通过Matlab的Curve Fitting Tool工具箱对实验数据进行多项式拟合，曲线如图2所示.

图2 SOC-OCV关系曲线图

通过拟合关系，可以得出SOC-OCV的对应关系如下：

f(SOC)=39.06SOC5-103.4SOC4+101.2SOC3-

44.79SOC2+8.806SOC+2.678 .

(4)

1.2 参数辨识

通过HPPC混合脉冲充放电试验(常温25 ℃)完成对电池直流内阻R0的测试，由放电时刻电压差与该时刻放电瞬态电流的比值得R0=17.4 mΩ，在Matlab中运用指数拟合的方式可以求出R1、R2、C1、C2相关参数。具体过程如下。

结合图1的等效电路模型，其端电压输出方程为：

V(t)=VOC(t)-i(t)R0-i(t)R1(1-e-t/R1C1)-i(t)R2(1-e-t/R2C2)，

(5)

拟合函数为：

V=a0+a1e-λ1t+a2e-λ2t.

(6)

由试验所得数据拟合结果，通过式(5)、式(6)对应系数相同的方法求得各参数见表1。

表1 参数辨识各值

高低温放电曲线如图3所示。由图3可知，当温度低于0 ℃左右时，电池的容量保持率以及对外放电电压的衰减程度较高温情况下更为明显，且影响着电池放电的整个阶段。考虑到温度对电池内部离子化学性能的影响，欧姆内阻表现出了较大的敏感性[6]。以25 ℃为基准，在不同温度下进行HPPC试验，得到不同的R0与基准条件下值的比。如图4所示，欧姆内阻在低温条件下较基准温度有明显变化，而在40 ℃往上的高温条件下表现平缓。根据拟合曲线可以获得关于R0的偏差控制量G(T)。

图3 高低温放电曲线

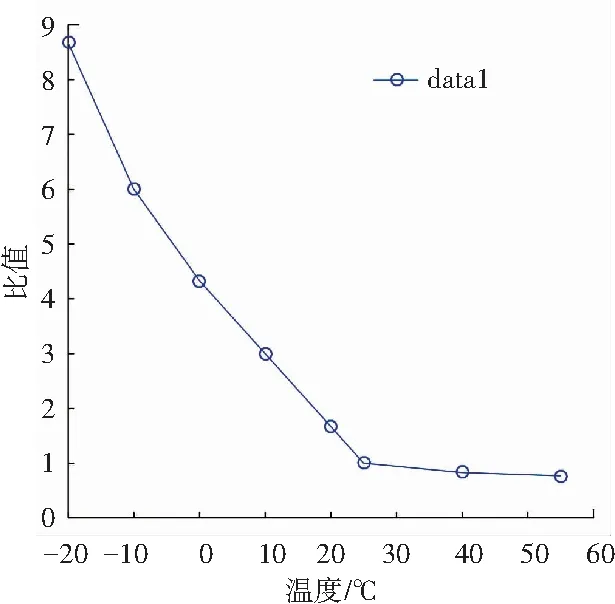
图4 相对25 ℃环境下的R0比值

2 改进的扩展卡尔曼滤波

实际SOC估算通过有效结合各方法的优势，进而达到准确估算的目的。

2.1 开路电压法

电池在满足时长的静置条件下，根据开路电压与SOC的对应关系，通过对开路电压的测量直接得出SOC，特别是放电的初末阶段，估算效果最佳。本文通过该方法获得较准确的初始电量。

2.2 安时积分法

基于电池模型的安时积分法是对电流进行积分来估算SOC的，通过实时监测电池的进出电量，再积累电量，得到该时段的电池充放电量。当前电池SOC状态可表示为：

(7)

其中，SOC0为初始电量；i(t)为充放电电流；Q0为电池额定容量；η为库仑效率。

结合2.1节的开路电压法获得较为精确的初始SOC值，由式(7)可直接计算得SOC值，库伦效率取值为1。该方法在长时间执行后，会产生较大的积累误差，从而影响最终估算精度。

2.3 扩展卡尔曼滤波法

由于电池在充放电过程中处于一个非线性的过程，扩展卡尔曼滤波法(EKF)引入了时域的概念，以状态方程完成对动态过程的描述，将局部非线性化的系统通过泰勒展开，除去高阶项，保留一阶及以下项，获得线性化系统。通过前一时刻的状态估计值与当前时刻的观测值进行递归，达到更新状态变量的估计。

系统状态方程与观测方程如下：

xk=Axk-1+Buk-1+wk-1，

(8)

yk=Cxk-1+vk-1，

(9)

其中，xk是系统的状态变量；uk为系统激励；yk是系统的观测变量；wk和vk分别表示系统的过程激励噪声和观测噪声。等效电路模型及式(1)～(3)将状态方程离散化可以求得矩阵A，B，C分别为：

(10)

EKF的递归步骤如下：

Step1初始化x0，P0；

Step2预测状态估计。其数学公式为：

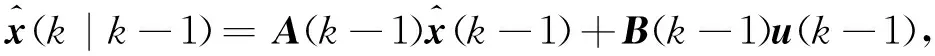
(11)

Step3误差协方差矩阵的时间更新。其数学公式为：

P(k|k-1)=A(k-1)P(k-1)AT(k-1)+Q,

(12)

Step4Kalman增益矩阵更新。其数学公式为：

K(k)=P(k|k-1)CT(k)[C(k)P(k|k-

1)CT(k)+R]-1,

(13)

Step5状态估计测量更新。其数学公式为：

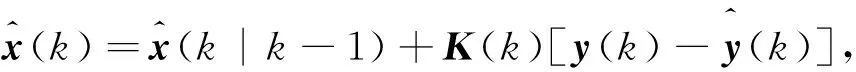
(14)

Step6误差协方差矩阵测量更新。其数学公式为：

P(k)=[I-K(k)C(k)]P(k|k-1),

(15)

Step7依次重复以上步骤。

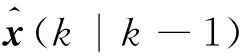
结合实际低温状态下电动汽车的冷启动及起步加速情况，为了提供更精确的SOC估算，本文针对观测方程引入了偏差控制量G(T)。通过对不同温度下欧姆内阻的调整实现了SOC估算精度的提升。

拟合的G(T)可以表示为：

G(T)=mT2+nT+p,

(16)

观测方程更新如下：

yk=Cxk-1+G(T)+vk-1.

(17)

其中，G(T)表示非线性的偏差控制函数，当T≥10 ℃时，G(T)趋于0；当T<10 ℃时，根据各试验及累积经验进行参数拟合得式(16)。

本文选用开路电压法获得较为准确的初始SOC，通过改进的EKF算法对k-1时刻SOC进行误差修正，最终通过安时积分法获得k时刻SOC估算值。

3 试验验证

本文考虑环境温度对R0的影响，通过大量试验显示高温情况下R0表现不敏感，而在低温情况下R0表现出较大的偏差。以下试验在Matlab的平台下进行仿真模拟。仿真环境选为-20 ℃，分别比较了加入偏差控制量前后EKF算法的估算误差，如图5～图8所示。

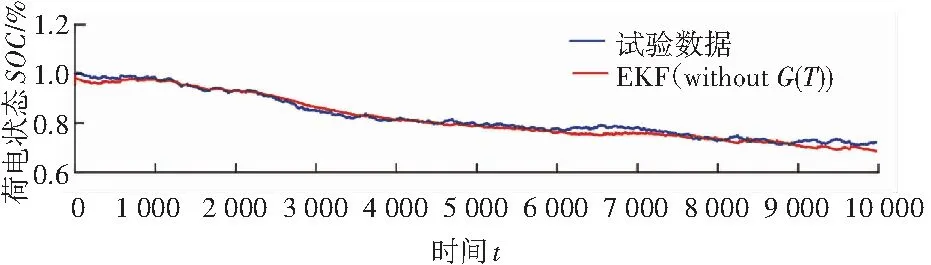
图5 试验数据和EKF(without G(T))的SOC曲线

图6 试验数据和EKF(without G(T))的SOC误差曲线

图7 试验数据和EKF(with G(T))的SOC曲线

图8 试验数据和EKF(with G(T))的SOC误差曲线

在不加偏差控制量的情况下，由图5可知，EKF的曲线趋势与试验数据的曲线趋势基本一致，图6显示EKF与试验数据之间SOC的相对误差控制在4.56%以下。在加上偏差控制量的情况下，由图7可知，试验所得曲线与改进后EKF的曲线吻合度更高，且由图8可知，二者相对误差控制在3.12%以下。结果表明，改进后的算法在一定程度上提高了SOC的估算精度。