一维有限深势阱中Ehrenfest定理的证明与验证研究

周启航，赵晓东，张海丰*

(1.佳木斯大学 理学院，黑龙江 佳木斯 154007；2.延边大学 护理学院，吉林 延吉 133002)

众所周知，一维方形势阱是非相对论量子力学中能够严格求解的基本物理模型之一，在很多方面得到了广泛的应用和研究，例如：孙康瑶对无限深势阱中全同粒子本征问题进行了数值模拟[1]；胡明飞成功的讨论了二维无限深圆方势阱中的定态几率分布问题[2]；杨梓骞给出了一维有限深方势阱中能量算符的数值解和近似解[3]；柳飞对一维无限深方势阱中的力算符进行了详细研究[4-5]；杨红卫对三维无限深势阱进行了可视化研究[6]；赵文静研究了半无限深势阱中自旋相关玻色-爱因斯坦凝聚[7]。另外，Ehrenfest定理作为能量表象中的重要定理之一也被得到了大量的研究和应用，例如：张运海在纠缠态表象下给出了广义Ehrenfest定理[8]；Vidal A.研究了一维箱势阱中的Ehrenfest定理和玻姆量子势[9]；Lijo T.给出了光得Ehrenfest定理及其非经典态[10]。本文旨在一维有限深方势阱中证明Ehrenfest定理成立，并利用一维无限深势阱的基态和第一激发态波函数构造出体系任意时刻的波函数，以此对推导的Ehrenfest定理加以验证。

1 一维有限深势阱中Ehrenfest定理的证明

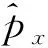
根据薛定谔方程及其共轭方程

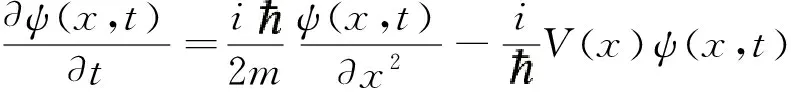
(1)

(2)

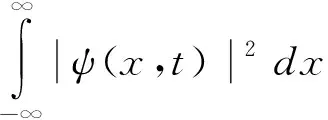
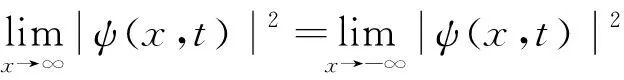
(3)

(4)

于是坐标x算符的平均值〈x〉对时间的导数为

(5)

于是将式(1)和(2)代入上式可知

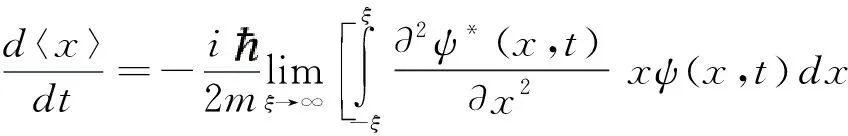
(6)

对(6)式采用分部积分后得到

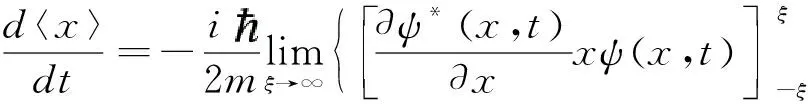
(7)

按照极限条件式(3)和(4)可知，式(7)可以变为

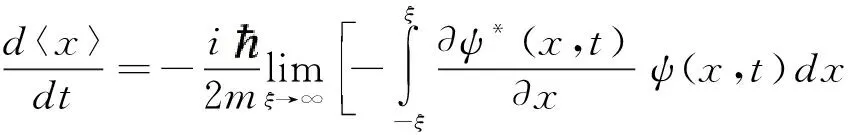
(8)

对第一分项分部积分得出

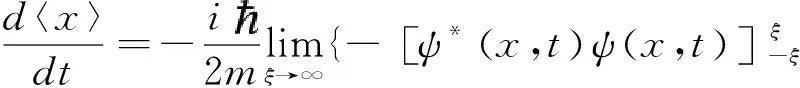
(9)

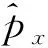
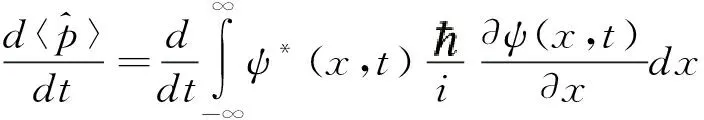
(10)

对ψ(x,t)的导数中可以交换对时间和空间的求导次序并利用薛定谔方程(1)则上式可以变为

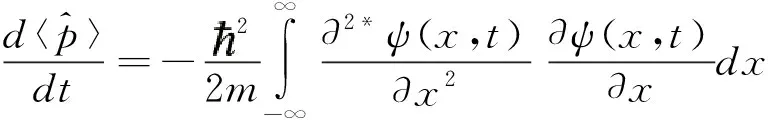
(11)

对上式第一项取部分积分可知

(12)

按照极限条件式(3)和(4)可知，式(12)变为

(13)

对上式进行分部积分可得

(14)

所以式(11)变为

(15)

2 Ehrenfest定理的验证

设t=0时刻，体系处于上述一维无限深势阱的基态和第一激发态波函数线性组合态上，即

ψ(x,0)=αψ1(x)+βψ2(x)

(16)

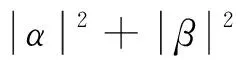
(17)

设一维无限深势阱的哈密顿算符的含时定态波函数为

(18)

按照状态叠加原理可知，对于任意时刻

(19)

所以坐标算符平均值〈x〉可以表示为

(20a)

进一步推导可得

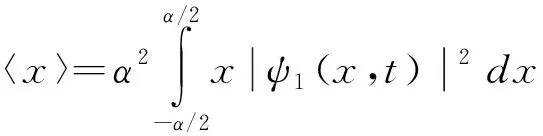
(20b)

下边计算上式的各个积分

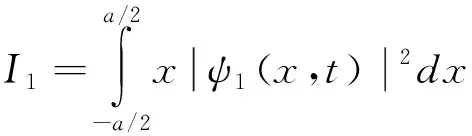
(21)

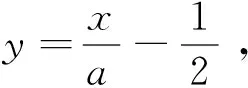
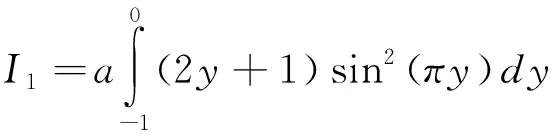
(22)

所以

(23)

同理

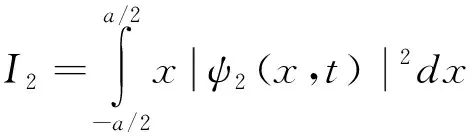
(24)

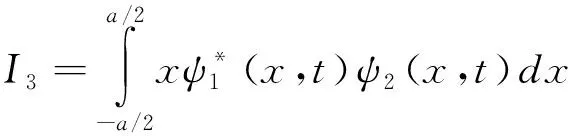
(25)

(26)

所以

(27)

进一步计算可得

(28)

所以

(29)

(30)

对于上式，根据函数的奇偶性可得

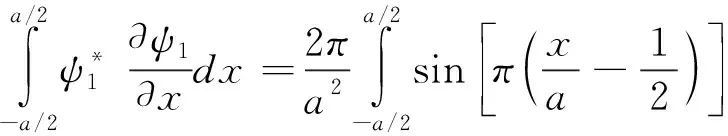
(31)

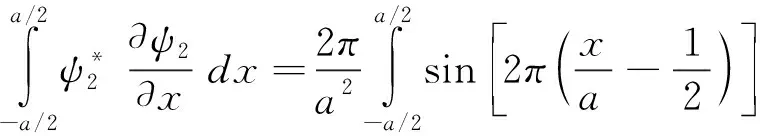
(32)

(33)

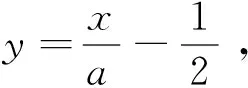
(34)

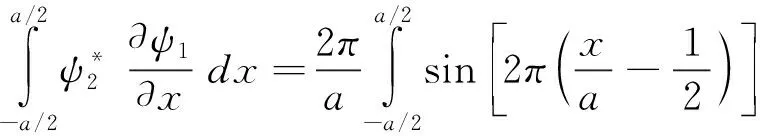
(35)

使用上面同样的定义，我们得到

(36)

所以

(37)

比较式(29)和(37)可知，两式的结果完全相同，即Ehrenfest定理得以验证。

3 结论