基于K-means彩色图像分割的六价铬检测方法
2020-04-28张明杨刘睿凡丁建军
孙 超,张明杨,杨 飘,刘睿凡,齐 卉,丁建军
(江汉大学 物理与信息工程学院,武汉 430056)
0 引 言
六价铬化合物是电镀等工业工艺产生的常见重金属污染物,它是可吞入性毒物,极易被人体组织和器官的细胞吸收,通过消化道侵入时易引起呕吐和腹痛[1-2]。传统的六价铬检测方式大多数是应用分光光度法的原理进行测量作业的,其测量原理是在被测水样中添入磷酸、硫酸,然后向水样添加二苯碳酰二肼使之与六价铬反应,用紫外线将生成的紫红色化合物按照分光光度法进行测量,从而得到受检样品中六价铬化合物具体的含量信息[3-5]。但是这些方法使用的试剂量大且无法现场检测,且检测时反应时间过长[6-8]。
当含有六价铬离子的溶液与检测试纸发生反应后,试纸的前端方形区域会呈现出紫红色。由于只有前端部分能够代表六价铬离子的浓度,因此在提取试纸图像的颜色特征前,需要先对该部分进行图像分割获取目标区域[9-11]。
传统的图像分割方法主要有基于边缘分割、基于阈值分割和基于区域分割,依据灰度值的不同对图像进行分割。不同的区域会有不同的灰度值,区域之间的边界处,会有明显的灰度变化。如果将彩色图像转换为灰度图像后再使用基于阈值的分割方法,彩色图像特征信息会丢失,从而造成分割不准确[12-13]。
本文在试纸检测法的基础上,利用机器视觉系统获得图像并处理数据,从而达到在现场快速实时监测的效果。该方法依靠机器视觉系统获得目标图像信号,得到目标像素、亮度和颜色等形态信息进行各种运算来提取的目标特征,并进行自动识别或根据判定结果来控制现场设备,从而达到高灵活度和高度自动化的生产效果。
1 K-means聚类的彩色图像分割
本文对六价铬检测试纸的彩色图像所选取的分割方法正是与K-means均值聚类结合的图像分割算法。图像获取边缘的步骤如图1所示。
图1 获取图像边缘的步骤
聚类算法就是将具有不同特征的数据分别归类,聚集形成新的具有相同特征的各个数据小类[14-15]。K-means聚类代表着个数为N的总数据中,输入聚类的个数为K,K值可以按照算法要求自行设置。图2给出了一种简单理解K-means聚类的图解方式。
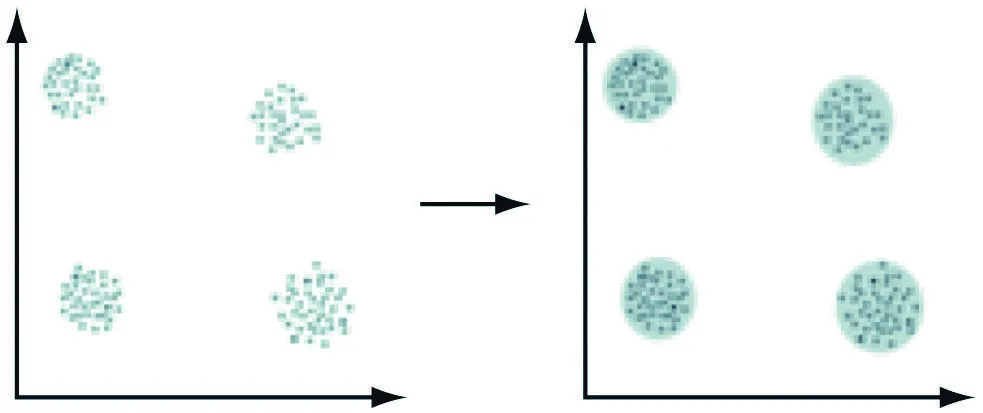
图2K-means聚类图解
首先,输入K个聚类个数和数据总数N,然后在N里随机选择K个点作为聚类中心,计算出所有点到这K个聚类中心的距离,将该点归类到距离最小的一个聚类中心。形成了新的类后,将该类的数据平均值作为新的聚类中心。
如果重新计算后的结果与上一次计算结果相同,则表明此时的计算结果已经满足收敛准侧,可以输出聚类结果。图3为K-means算法的流程步骤。
图4是一个当K取值为2时的简单算法概要图。在总数为5的数据(A、B、C、D、E)里,选择2个种子点,即K的取值为2。
然后开始进行如下操作:①随机在图中取K(这里K=2)个种子点。②计算出A、B、C、D、E到种子点的距离,选择最近的一条链接。在图中可以看到,图片上端的种子点距离A和B较近,下端的种子点距离C和D较近。③将种子点移至数据点群的中心。④重复进行上述的操作,直至数据群里没有可以移动的种子点。这时可以得出聚类的结果:A、B、C被图中上端的种子点聚合;D、E被下端的种子点聚合。

图3K-means算法步骤

图4K-means算法概要图
一般来说,求点群中心点的算法可以很简单地使用各个点的X/Y坐标的平均值。本文探讨另3个求中心点的公式:
(1) 当λ随意取值,可以是负数,也可以是正数,或是无穷大。Minkowski Distanceshi是以星形的方式逼近中心,
(1)
(2)λ=1,以菱形方式逼近中心,
(2)
(3)λ=2的情况,
(3)
在Matlab中,利用K-means聚类算法实现彩色图像分割的具体步骤如图5所示。
对K-means算法分析可以发现,当K的取值越大时,图像的分割效果越好,但是相应地,程序响应时间会变得更久一些,所以决定K的取值成为研究需要权衡的一个因素。因为颜色空间有3个通道,所以本文将K的取值设置为3,得到每个通道聚类的图像。分割后的结果如图6~8所示。

图5K-means彩色图像分割流程
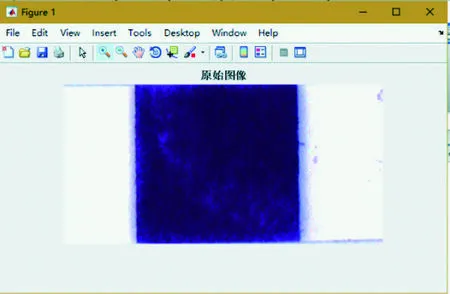
图6 K-means聚类分割原始图像

图7 K-means聚类分割聚类结果
本文采取了基于K-means聚类分割的方式的优点,提出了一种基于聚类算法的彩色图像分割方法,将六价铬检测试纸图像中的反应区域清晰分割出来。K-means分割的结果十分清晰,而且可以直接在彩色图像上进行操作。与基于边缘的分割算法相比,图像的分割效果更好。
2 试纸彩色图像结果读取
基于分光光度法测量六价铬含量的原理,检测试纸与含六价铬溶液反应后,试纸的图像信息就代表着六价铬浓度。为了进一步探究图像所显示的信息与六价铬溶液浓度的具体关系,本文采用RGB彩色空间模型,将试纸的R、G、B3个颜色分量数值提取出来,利用mean 2()函数计算出R、G、B颜色分量的具体数值。
Mean 2()函数的功能是对一整个矩阵求像素平均值。在M×N的目标区域图像中,每个颜色分量通道都形成了一个单独的矩阵,利用mean 2()可以求得整个矩阵的像素平均值,R、G、B分量计算公式如下:
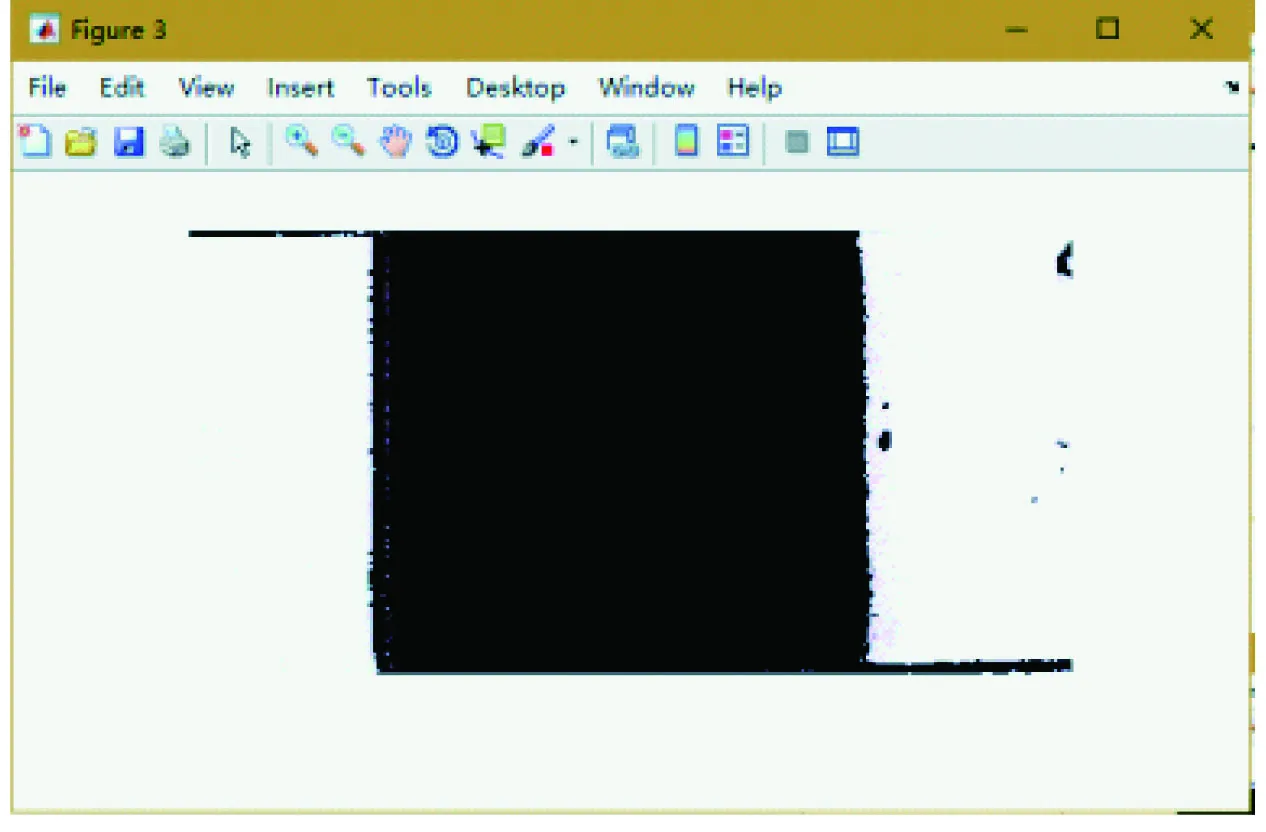
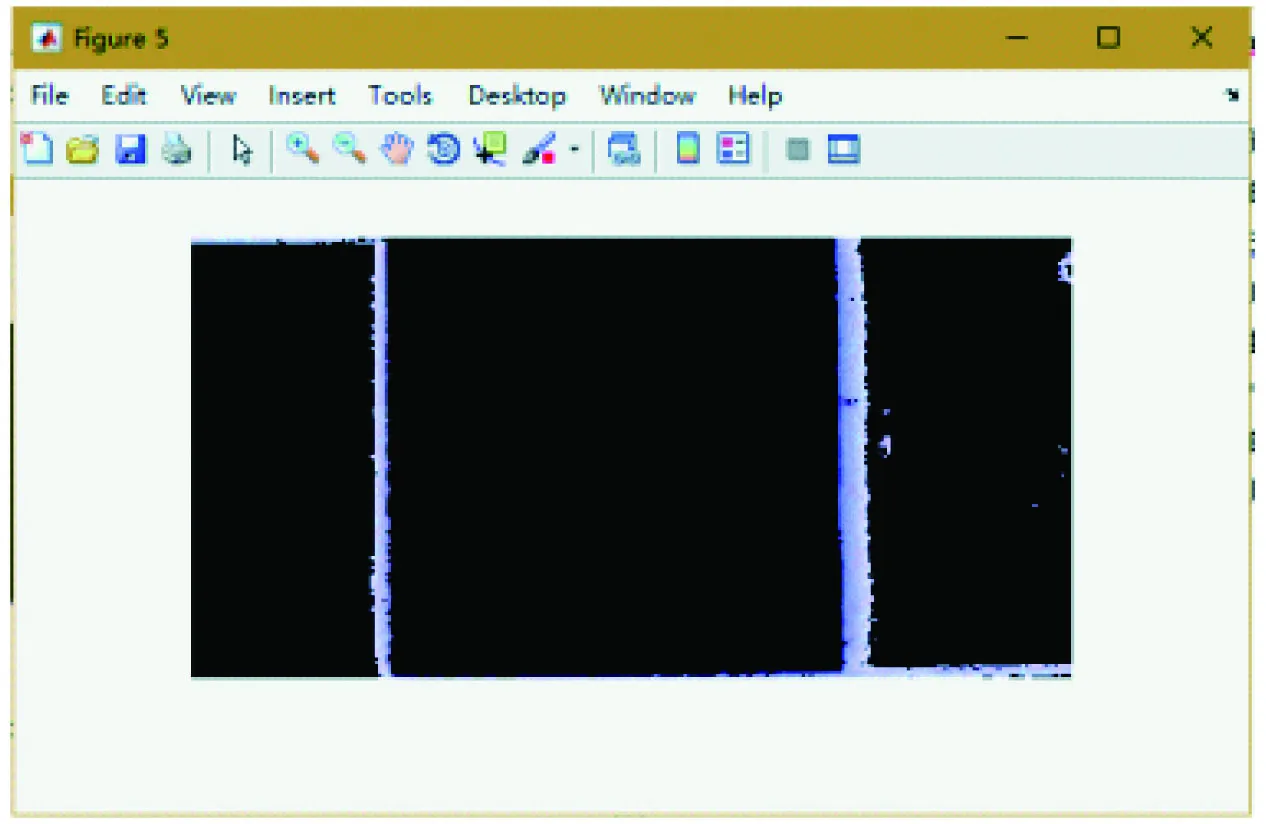
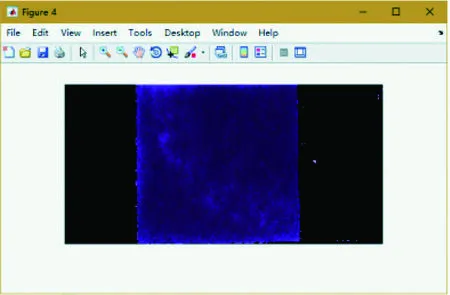
图8 K-means聚类分割通道1、2、3图
(4)
(5)
(6)
本文选取了22种浓度的六价铬标准液与检测试纸进行反应,将得到的反映区域图像作为颜色特征提取的对象。在相同温度、光照等条件下进行图像采集,对图像进行滤波去噪并使用K-means聚类算法提取出目标区域图像,结果如图9所示。
实验测得变量之间的22个数据,在空间内绘制出得到六价铬试纸图像特征的散点图。从图中可以大致看出这些点随机散落在某直线附近,可以认为R、G、B的值与被测溶液中六价铬离子的浓度之间近似为一线性函数。
显然,从图中可以发现随着浓度的减少,三原色向量呈线性增长,颜色特征R分量和颜色特征B分量与六价铬离子浓度呈凹曲线状,如图10、11所示。而颜色特征G分量对于浓度变化有更为灵敏的反应,如图12所示,浓度区间在0~40 mg/L时,该曲线斜率陡增。



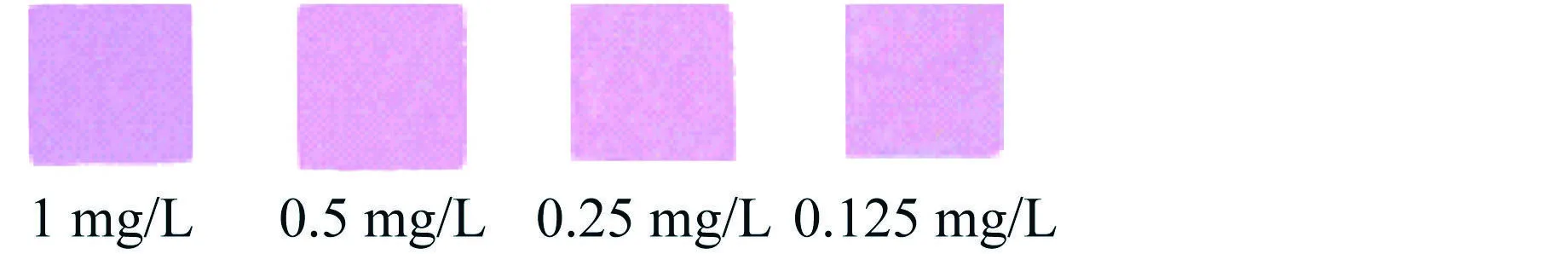
图9 22种标准溶液反应的试纸图像目标区域图像
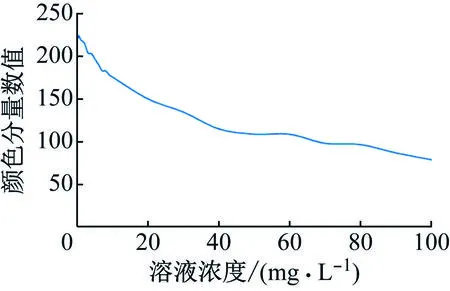
图10 R分量与浓度的关系图
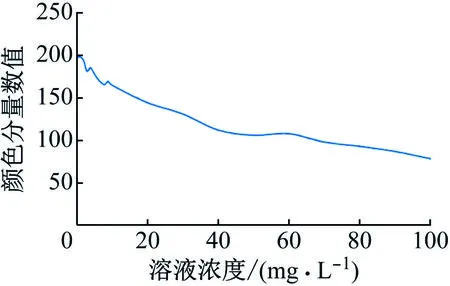
图11 B分量与浓度的关系图

图12 G分量与浓度的关系图
将使用mean 2()函数提取到的R、G、B的平均值导出,得到3种颜色特征分量数值,拟合后,得出的结果如下:

0.016 8x1x2-0.341 4x1x3+0.044 6x2x3+
0.923 2x1-0.102 1x2-3.544 2x3+278.488 6
根据程序的运行结果,可以得到该函数的判定系数为0.995 9,F检验值为327.045 2,误差方差为7.662 5。在Matlab中,通过rcoplot()函数画出残差个案排序图形,以此来是否为异常值样本,程序中运行的结果如图13所示。
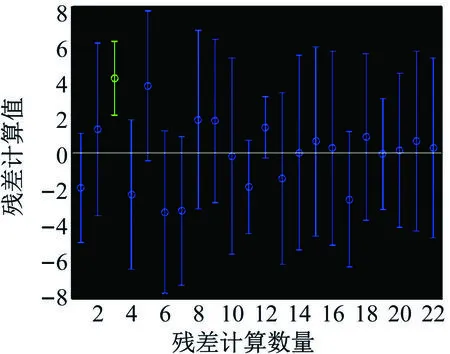
图13 残差图
运用此模型对该回归模型检验中,判定系数R2为0.995 9,非常接近于标准值1,说明回归方程显著。而P值检验为5.990 2×10-13,可以判定该模型拟合度较好,通过了模型回归检验。
3 结 语
针对传统使用试纸显色法比色的过程中,根据光照、个人视力等多种因素影响,只能得到一个粗略的浓度范围,为了获得更加精准的浓度值,本文采用一种基于机器视觉的六价铬离子检测方法来实现对水体六价铬离子残留浓度的快速检测。
针对传统基于边缘的图像分割方法,仅以图像灰度值的明显变化作为边缘识别的依据,对于彩色图像来说,没有充分考虑全局信息。本文提出了一种基于聚类算法的彩色图像分割方法,将六价铬检测试纸图像中的反应区域清晰分割出来,完成了该算法的仿真和实现。对比分割后的试纸彩色图像可以看出,使用本文提出的算法,与基于边缘的分割算法相比,图像的分割效果更好。
