转向工况下的分布式电动汽车稳定性控制

郭烈 葛平淑 许林娜 林肖

(1.大连理工大学 汽车工程学院，辽宁 大连 116024；2.大连民族大学 机电工程学院，辽宁 大连 116600；3.大连理工大学 控制科学与工程学院，辽宁 大连 116024)

全球能源问题的加剧推动了新能源汽车发展的脚步，加快研究和构建推动节能汽车是我国汽车产业发展规划的战略目标之一[1]。分布式驱动电动汽车因其污染少、耗能低以及各轮力矩可单独控制的特点成为行业的热点[2]。实际应用中如何利用其独特优势来提高车辆安全性、降低交通事故是目前电动汽车研究的关键技术之一。

目前，关于车辆转向稳定性研究主要集中在力矩分配和控制算法研究方面。例如He等[3]利用主动转向的变转矩分配控制来提高车辆的操纵稳定性；王庆年等[4]利用七自由度动力学模型对四轮独立驱动电动汽车的转向驱动进行控制，改善车辆的操纵性和稳定性。稳定性控制主要采用滑模控制和模糊控制算法，但滑模控制器易产生抖振，若消除抖振又会降低抗干扰性[5]，很难达到理想效果。模糊控制器虽有解决非线性问题的优势，但其控制规则复杂，隶属度函数也需根据成熟经验获得[6]，因此也不能作为稳定性控制的最佳选择[7]。力矩分配方面，普遍采用平均力矩分配或垂直分配方案[8]，这两种力矩分配方法虽然原理简单，但没有充分利用轮毂电机驱动电动汽车各轮独立可控的优势。Demirci等[9]提出了3种不同的电动差速器控制方案，通过不同车速下的助力转向特性曲线来计算两转向车轮之间的差动转矩，Lin等[10]利用多个目标同时优化的方法进行稳定性的提升，并对目标函数进行简化，虽然在理论上提高了系统的优化率，但却破坏了整体性，反而使优化准确性降低。

适当的控制策略及合理的力矩分配可以使车辆稳定前进的同时获得较高的动力性。本研究以分布式电动汽车为对象，设计基于粒子群算法的神经网络比例-积分-微分(PID)优化算法跟踪期望横摆角速度的稳定性控制和最优力矩分配算法，兼顾车辆稳定性和动力性，最后验证算法的可行性和正确性，使分布式驱动电动汽车可以达到期望要求。

1 转向稳定性控制器设计

1.1 转向动力学模型分析

建立合理准确的部件和整车动力学模型可正确反映其动态特性，提高准确性。为了更好地研究分布式驱动电动汽车转向稳定性的基本特性，将汽车模型简化为平面四轮的动力学模型，如图1所示。忽略汽车的垂向位移、绕横向的俯仰运动和绕纵向侧倾运动，只考虑车辆在x轴的纵向运动、y轴的横向运动和绕z轴的横摆运动[11]。

图1中vx、vy分别为车辆纵向、横向速度，β为质心侧偏角，γ为横摆角速度。Fx1、Fx2、Fx3和Fx4分别为车辆左前、右前、左后和右后轮的纵向力，Fy1、Fy2、Fy3和Fy4分别为车辆左前、右前、左后和右后轮的横向力。δf为前轮转角，lf、lr分别为质心到前、后轴的距离，lw为轮距，αf、αr分别为前、后轮侧偏角。

汽车沿x轴的纵向运动方程为

Fx=(Fx1+Fx2)cosδf+Fx3+Fx4

(1)

汽车沿y轴的横向运动方程为

(Fy1+Fy2)cosδf+Fy3+Fy4

(2)

汽车绕质心的横摆运动方程

(3)

车轮的动力学方程为

(4)

式中：m为整车质量、Iz为车辆绕z轴转动惯量、Mx为横摆力矩、Jω为车轮转动惯量、ω为车轮角速度、Td为驱动力矩、Te为干扰矩、r为车轮半径。

考虑实际道路情况下，横摆角速度必须受地面附着力的限制，即横摆角速度应该小于地面允许附着力的0.85倍[12- 13]，超出安全裕度时，应受到约束

(5)

式中：γdes1为超出安全裕度时的理想期望横摆角速度、R为转弯半径、系数K计算公式为

式中：Cf和Cr分别前轮和后轮的侧偏刚度。

定义

(6)

式中：γdes2为不超出安全裕度时的理想期望横摆角速度、μ为摩擦系数，g为重力加速度。

则理想横摆角速度γdes为

(7)

1.2 整车模型搭建

利用Simulink分别搭建驾驶员速度模型、横摆角速度模型、4个滑移率控制器模型、4个电机模型和力矩分配模型，Carsim接收4个电机传来的力矩，同时将车速、转速等所需信号传至Simulink中进行相应控制。在S函数里编写整个控制算法以形成完整的联合仿真。驾驶员模型以目标车速和实际车速间的差值作为驾驶员速度控制器的输入，利用电子油门特性图对油门开度进行查表，找到当前开度所对应的输出力矩作为车辆的速度输入力矩，滑移率控制器和横摆角速度控制器输出力矩共同作用输出给各个车轮。

1.3 转向稳定性控制器设计

转向稳定控制器分别由横摆角速度控制器和滑移率控制器组成。控制器设计如图2所示，采用经过粒子群修正的神经网络PID控制器，可以克服神经网络收敛速度较慢和易陷入局部最优解的问题，从而达到理想控制效果。

图2 转向稳定性控制器设计

首先采用反向传播(BP)神经网络建立在线参数自学习的PID控制器。利用控制器找到跟踪参数误差下比例、积分和微分的最佳值，使理想横摆角速度和实际理想车轮角速度和实际车轮角速度的误差最小。BP神经网络算法存在收敛速度慢和易陷入局部最优解的缺陷[14]，对权值进行改进有效解决了收敛速度慢的问题，而粒子群可以对全局求优，两者结合可以有效改善神经网络算法的缺陷，算法流程如下：

(1)初始化神经网络权值。选取3- 5- 3的网络结构，粒子群种群即初始权值规模选为25，加速因子c1和c2的值均设置为2，惯性权重设置为0.9；用n来表示当前的迭代次数，初始化为0；设定最大迭代次数为50。

(2)计算神经网络权值的适应度。将BP神经网络中输入的横摆角速度误差和由滑移率所计算的角速度误差作为目标函数，计算公式为

(8)

式中：fi为权值i的适应度，ej(n)为第n次迭代时第j层的网络误差。

(3)更新粒子群参数。根据式(9)和(10)更新神经网络权值的速度和位置[15]：

(9)

(10)

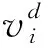
(4)判断是否达到终止条件。假设Epso是本次寻找到的全局最优权值，并假设一个无限接近0的正数ε。如果当前权值E与全局最优权值Epso的误差在给定范围内，即|Epso-E|<ε，则表明本次寻优达到终止条件，即得到了粒子所代表的最优输入、输出初始权值wi、wo，如果不满足，返回步骤(2)，进行新一轮迭代。

(5)根据以上流程计算最佳初始神经网络权值，随后利用BP神经网络得出控制器的最优参数Kp、Ki和Kd，最后根据车辆模型计算最优横摆力矩和滑移率力矩。

2 驱动力矩最优分配控制算法

2.1 转向工况下驱动力矩的修正

通过对两前轮的驱动力矩进行修正提高车辆转向时的稳定性和动力性。由动力学模型可知，左、右前轮驱动力产生的力矩差ΔTc可写为

(11)

式中：Tc1、Tc2分别为左、右前轮驱动力产生的力矩、Td1、Td2分别为左、右前轮驱动力矩、ΔTd为左、右前轮驱动力矩差。

因此，汽车在转向工况下，若车辆外侧车轮的转矩大于内侧车轮转矩，在整个转向过程中会对驱动力矩进行修正。

(12)

式中：T1′、T2′分别为左、右前轮的修正驱动力矩。

通过调节ΔTd的大小来对驱动力矩进行调节，增加转向过程中的动力性和稳定性。利用模糊控制算法得到ΔTd的值，以驾驶员的输入转角以及转角变化率作为修正驱动力矩控制器的输入，车辆左前轮和右前轮的转矩差为输出，最后根据驾驶员的转向经验建立模糊控制规则。

对分布式驱动电动汽车的驾驶转角信号进行采集，得出前轮转角以及转角变化率的取值范围，前轮转角论域取为[-60，60]，规定车轮左转向时为正，右转向时为负，前轮转角的模糊论域[-60，-40，-20，0，20，40，60]定为7个模糊子集[NB，NM，NS，ZO，PS，PM，PB]，每项隶属度函数都为三角函数。前轮转角变化率范围为[-1，1]，取其模糊论域范围为[0，1]，模糊语言子项定为[FA，MI，SL，ZO]，以此表示操作过程中转向角的速度变化需求，同样采用三角形隶属度函数。模糊控制器的输出为左、右前轮的纵向转矩差，将其论域定为[-80，80]，其模糊语言表示为[NB，NM，NS，ZO，PS，PM，PB]。根据驾驶员的转向经验设定模糊控制器分配给左、右前轮转矩差的模糊规则，模糊规则见表1，输出最终驱动力矩，然后进行下一步的最优力矩分配计算。

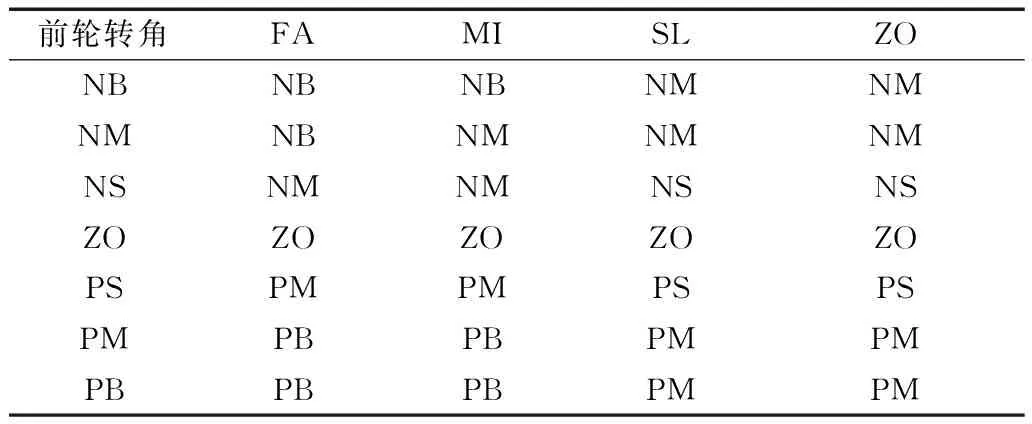
表1 模糊规则表

2.2 最优力矩分配策略

目标函数是在考虑电机能量损失、控制力矩补偿以及轮胎附着利用率等多目标约束下，进行集成化力矩分配方式。

为使力矩分配控制器的实际执行力矩分配器与横摆力矩控制器计算力矩之间误差尽可能小，目标函数的第1项可写为

V1=B1u

(13)

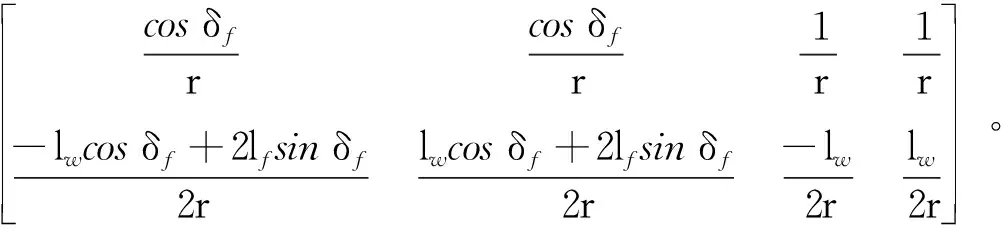
引入轮胎利用率的概念，轮胎利用率是指轮胎受到的地面反作用力与其发生抱死前的极限受力之比，通常以此来反映车辆的稳定程度[16]。

(14)

式中：ηi为第i个车轮的轮胎利用率；i=1，2，3，4，分别表示左前轮、右前轮、左后轮和右后轮。

目标函数的第2项是使得4个车轮的轮胎利用率之和尽可能小，保证汽车的安全性。

在利用二次规划进行求解目标函数时，为了使‖B1u-V1‖尽可能最小，在此引入权重系数ξ，最后形成的范数形式目标函数为

(15)

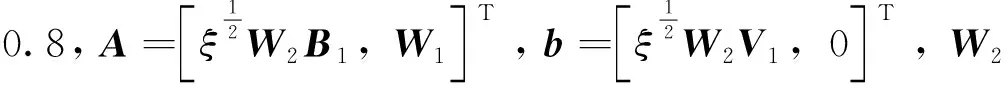
当车轮出现滑转现象时，车轮与地面间的横向力和纵向附着力都会大大降低，车辆将处于非常危险的状况，为了防止车轮在行驶途中发生过度滑转的危险，考虑将4个车轮的滑移率调整力矩作为第1项约束条件，将其转化为二次规划问题中等式约束的数学形式

(16)

式中：si表示第i个车轮的滑移率系数，Tsi表示第i个车轮的滑移率调整力矩；i=1，2，3，4，分别表示左前轮、右前轮、左后轮和右后轮，若实际滑移率大于最大滑移率，则si=1，否则，si=0；Ts表示滑移率调整力矩向量。

约束条件第2项：车辆在行驶过程中必须处于电机力矩可允许范围内[17]

Tb max≤Ti≤Td max

(17)

式中：Tb max为电机能够给予的制动力矩极大值，Ti为第i个车轮的驱动力矩，Td max为电机所能够给予的驱动力矩极小值。

约束条件第3项：力矩分配器以轮胎附着力作为第2个目标函数，因此考虑轮胎力饱和限制，即

(18)

根据上述目标函数和约束条件，可以得到二次规划标准式如下

minQ=‖Au-b‖2

(19)

式中：umin为驱动力矩最小值矩阵、umax为驱动力矩最大值矩阵。

对上述二次规划问题采用有效集法进行求解，其最大难点在于不知道有效集，可构造几何序列去逼近[18]，将约束条件中的不等式写为矩阵形式。

选择驱动力矩矩阵的起始点u0，用Ф表示在该点处的有效约束指标集，定义N为总的搜索次数，dk为沿着梯度最小方向下降的步长，设定uk沿着dk方向搜索，k=0，1，2，…，N-1，将两个约束指标看成等式约束，上式可写为

(20)

若uk+di是问题可行解，则步长φk=1，uk+1=uk+di，根据下式求解出拉格朗日乘子

(21)

式中：Cmean为驱动力矩均值矩阵。

如果乘子λ2≥0，那么最优解就是uk+1，如果λ2<0，则将最小λ2所对应的约束条件移出约束指标集，进行下一次迭代。

若uk+di不是问题可行解，通过下式求出满足可行条件的最大步长φk，修正有效集序列。

φk=max{φk∈[0，1]：umin≤uk+φkdi≤umax}

(22)

令uk+1=uk+φkdi，将此迭代点与当前有效约束加入工作集中开始下一次更新，如此循环，最终找到可行域内最佳点。

3 仿真结果与分析

为验证所设计横摆力矩控制器与力矩分配策略的正确性和高效性，采用Carsim与Matlab/Simulink建立联合仿真平台，对所搭建的动力学模型和算法进行验证。在Carsim中设置车辆类型、车体尺寸参数等信息，如表2所示。

表2 整车参数表

仿真工况选用最能体现车辆转向特性的双移线工况和蛇形工况两种经典工况。

(1)双移线设置路面摩擦系数为0.5，车辆以100 km/h的速度进行实验，仿真结果如图3所示。

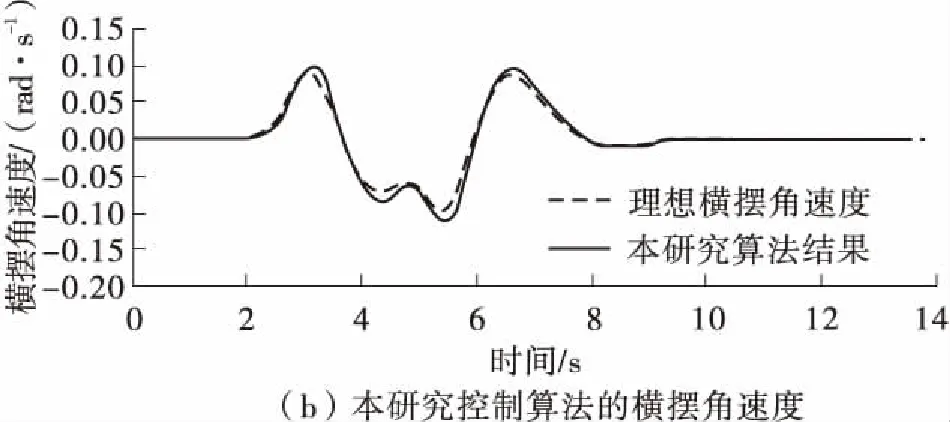
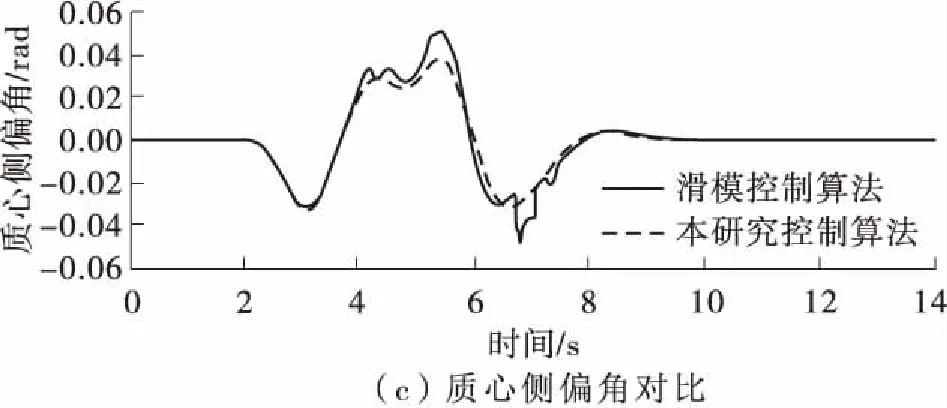
图3 双移线工况仿真结果

图3(a)、(b)分别示出了滑模控制和本研究所设计控制算法的横摆角速度，两种控制算法下，由式(5)计算得到的理想横摆角速度不一样，因此，分别画出其实际与理想横摆角速度的对比图。从图中可以看出，两种控制都可以使横摆角速度较好地接近理想值，但在横向位移最大时，滑模控制系统无法避免抖振的存在，最大正向横摆角速度震荡非常严重且数值上为0.124～0.126 rad/s，而经过本研究优化的BP-PID算法避免了抖振，能更好地跟随理想值，且最大值为0.09～0.10 rad/s。

图3(c)为质心侧偏角变化图，两种控制最大质心侧偏角都不超过正负0.058 rad，但本算法使得车辆的可控性提高了30.9%。图3(d)为在本研究所设计算法下的4个车轮的滑移率，各轮的滑移率都处于0.052以下，说明能满足汽车转向时的侧向稳定性，从以上数据可知，本研究转向稳定性控制算法在双移线工况下的稳定性提高了20.6%左右。

图3(e)、(f)示出了规则分配和最优分配的各轮力矩，以第6 s为例，从图3(a)可知，此时车辆处于右转状态且实际横摆角速度比目标横摆角速度大，说明车辆有过度转向的危险，在车辆处于不滑转的前提下，两种力矩分配方式都能使右侧车轮力矩大于左侧车轮力矩。这说明本研究提出的力矩分配算法为了调节过度转向的危险，分配了反向力矩阻止危险的发生，但由于目标函数考虑了载荷转移，前轴车轮力矩要大于后轴力矩并且比规则分配力矩差大22.7 N·m。因此转向工况下最优力矩分配在双移线工况下将转向稳定性提高了31.2%。

(2)蛇形工况将附着系数取为0.5，并以 80 km/h的速度持续前进，仿真结果如图4所示。

图4(a)、(b)分别示出了滑模控制和本研究所设计的控制算法下的横摆角速度，两种算法都能跟随理想值，但在横向位移最大时，由于滑模控制的严重抖振使响应图产生严重震荡，最大正向横摆角速度数值为0.19～0.21 rad/s，而采用本研究中优化的BP-PID算法时避免了抖振，克服了陷入局部最优缺陷，并能更好地跟随理想值，且最大值为0.17～0.20 rad/s。

图4(c)为质心侧偏角变化图，两种控制算法最大质心侧偏角均不超过正负0.085 rad，使车辆的可控性增加了15%。由图4(d)可以看出各轮的滑移率都处于0.055以下，说明能满足汽车在转向行驶中的侧向稳定性，本研究提出的算法能将蛇形工况下的打滑现象降低36.4%左右，最大转向稳定性提高了42.8%。

图4(e)、(f)示出了施加规则分配和最优分配的各轮力矩，以第2 s为例，从图4(e)可知，此时车辆处于右转状态，且实际横摆角速度比目标横摆角速度大，说明车辆有过度转向的危险，图中可以看出两种力矩分配方式都能使右侧车轮力矩大于左侧车轮力矩，这说明力矩分配算法为了调节过度转向的危险，分配了反向力矩阻止危险的发生。但由于本研究提出的力矩分配算法考虑了载荷转移，因此车轮力矩差比规则分配大182.5 N·m.从以上数据可得，转向工况下最优力矩分配将蛇形工况下的转向稳定性提高了15.7%。

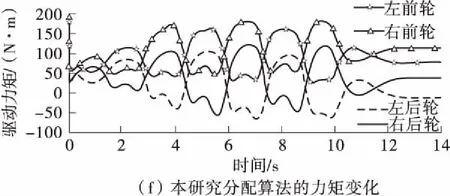
图4 蛇形工况仿真结果

4 结论

本研究探讨了以四轮轮毂电机驱动的分布式电动汽车的转向稳定性控制方法，基于车辆动力学模型设计了一种粒子群改进神经网络PID的横摆角速度控制算法，同时，通过模糊控制和二次规划算法实现各轮驱动力矩的最优分配，通过联合仿真软件对所提控制器进行仿真验证。双移线和蛇形工况仿真结果表明，本研究提出的稳定性控制算法能将车辆在转向时的稳定性平均提高23.4%，具有较好效果。考虑试验条件和工况危险程度，本研究仅进行了联合仿真验证，下一步拟在硬件在环试验平台或实车上验证所提控制算法的有效性。