基于优化Grid Search-SV M算法的服装版型分类预测研究
2020-04-28郑文靖
郑文靖
(西安工程大学 计算机科学学院,陕西 西安710048)
当前时代下,随着消费者对个性化穿着以及对服装尺寸适宜度要求的扩大,服装定制模式渐渐在国内占据了重要的市场份额。定制化是能够满足消费者对个性化追求的重要途径,在“互联网+”时代中,定制行为模式正发生着重要的变革[1-2]。
随着消费者需求的扩大,传统的定制模式可能对于众多的消费者来说,无法及时满足所有消费者的需求,因此实现服装定制推荐是当前服装定制市场的一种趋势。针对服装定制领域,目前国内主要聚焦于三维人体建模参与定制,并且多数强调的是款式、面料、部件样式的选择,忽略了消费者历史数据中有用的信息,因此,目前国内外服装定制推荐领域研究较少。文献[3]通过交互日志挖掘,采用有限状态机技术描述客户需求的会话交互行为模型,并运用约束满足理论和多属性效用理论,开发了一种基于约束满足和情感效用的个性化西服定制推荐系统;文献[4]基于Kinect描述了一种人体及服装重构的方法,由多个Kinect捕获人体模型,对服装进行3D建模,将其变形以适合人体,然后应用缝合将这些模式缝合在一起;文献[5]设计和开发了基于专家知识的个性化服装搭配系统,提供了个性化的服装搭配服务;文献[6]采用BDEU决策树算法,构筑了用户类别偏好模型,向用户提供了个性化的推荐服务。以上研究对于服装定制推荐领域的涉及有限,因此,本文致力于研究服装定制领域中的量体数据与服装版型。
在大数据时代下,为方便消费者快速选择适合自己的定制服装版型以及面料绣花搭配,通过SV M分类算法对众多量体数据进行挖掘分析,根据用户自身的量体数据进行计算后推荐给用户适合的版型,从而根据版型进一步实现用户的个性化定制搭配推荐。个性化的定制推荐与传统的定制选择相结合,才能为用户提供更好的定制服务。
1 量体特征值与版型类型的SV M数据模型
1.1 量体数据特征参数集初始化
设量体数据为输入样本X,以上衣量体数据为例,x1、x2、x3、…、xn分别为代表不同部位的量体特征值,如衣长、胸围、下摆、中腰、肩宽、袖长等部位,输入n个特征值作为样本值X(Xi)
建立量体数据参数集X={x1,x2,x3,…,xn}
由于量体特征值之间存在较大差异,如胸围与肩宽之间的差异。需对量体数据集进行归一化处理,使得参数空间在各维度分布均匀,模型具有较优的迭代速度和分类预测效果。归一化方法为:
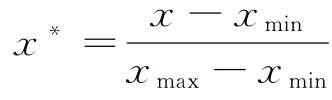
1.2 构造最优超平面
以上衣为例,设X={YC,X W,ZY,XB,JK,XC},YC、X W、ZY、XB、JK、XC分别代表衣长、胸围、中腰、下摆、肩宽、袖长,设Y=版型分类值,X与Y可表示为:
{(x1,y1),(x2,y2),…,(xn,yn),xt∈Rd,yt∈ {y1,y2,…,yn}}
此关系模式下必然存在n-1个超平面,将这些样本分别两两区分,最终实现分类效果,超平面可表示为:

式中,w∈Rd为该平面的权值法向量,b∈R为偏置量。
则样本到超平面的分类间隔为:2/‖w‖,由于原始样本空间数据的线性不可分性,因此,引入惩罚参数C来调整支持向量机对已知训练样本构建最优分类超平面时分类错误容忍程度[7]。所以要建立最优超平面的问题变成在有约束的条件下求:

1.3 计算最优解
为了解决构造最优超平面的问题,引入Lagrange函数[8]:
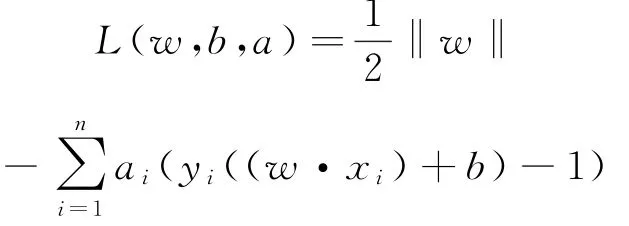
式中,ai≥0,i=1,2,…,n为拉格朗日乘子,为了求得w和b的最小值,对w和b求偏导数,并使得它们的偏导数为零,即:

对于已知训练样本 (xi,yi),求使得L(w,b,a)取得最大值时的ai,将二次规划问题转化为相应的对偶问题,根据Lagrange对偶性原理,将问题中的参数全部转变为仅以Lagrange乘子作为参数变量的目标式[9-10]:

解得最优解a*=(a1*,a2*,…,an*)'。最优法向量w和最优偏置量b分别为:

根据最优值,从而求得最优分类超平面(w*·x)+b*=0,则其对应的最优分类函数为:
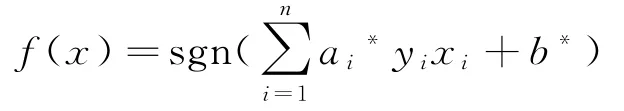
为实现样本空间从线性分划到非线性分划的过渡,引入径向基(RBF)核函数,将样本空间从低维映射到高维[11-12]。径向基核函数表达式为:

则最优分类函数为

2 基于优化Grid Search的SV M分类模型
2.1 Grid Search-SV M原理
惩罚参数C和核函数参数g是影响SV M分类器性能的关键参数[13],其中C表示模型对误差的容忍度。C值太大容易导致过拟合的现象,使得测试集的数据分类效果不佳;C值太小容易导致欠拟合,模型不能有效捕捉样本的数据特征,泛化能力变差。g是选择RBF函数作为kernel后,该函数自带的一个参数,隐含地决定了数据映射到新的特征空间后的分布,g越大,支持向量越少,g值越小,支持向量越多。g值过大过小,表明原始样本被映射至并不适用的高维空间,无法建立较优的分类模型[14-15]。
Grid Search是用在Libsv m中的参数搜索方法[16],在C和g组成的二维参数矩阵中,依次遍历网格内所有的点进行取值,对于取定的C和g利用K-CV方法得到在此组C和g下训练集验证分类准确率,最终取使得训练集验证分类准确率最高的那组C和g作为最佳参数。使用Grid Search算法可以得到全局最优,且C、g相互独立,便于并行化进行[17-18]。
基于Grid Search-SV M算法的服装版型分类识别,具体操作是在MATLAB软件中利用LIBSV M3.14工具包中的SV Mcg For Class.m函数,使用meshgrid方法构建网格,寻找最佳C和g参数,实现用Grid Search优化SV M参数和服装版型识别,算法如表1所示。
2.2 Grid Search-SV M模型建立
在版型分类预测的过程中,提取量体数据特征值,并进行归一化处理后,引入RBF核函数,将样本数据映射到高维空间,再进行SV M模型训练、参数寻优以及模型验证,整个版型的预测模型如图1所示。

表1 Grid Search-SV M算法流程

图1 Grid Search-SV M版型预测模型
(1)选定训练集与测试集,对数据集进行划分。
(2)样本数据预处理:为了避免各个样本因子之间量级的差异,减少样本之间的相互影响,同时保证程序运行收敛加快,需要对样本因子进行归一化处理[19-20],在MATLAB中用map min max函数实现其归一化。
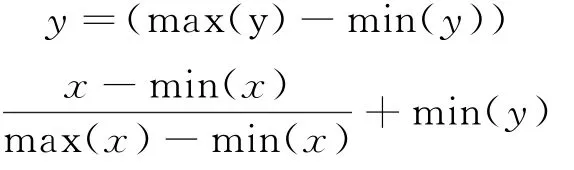
式中,x、min(x)、max(x)分别是原始样本数据及其最小值、最大值;min(y)、max(y)分别代表归一化后样本的最大值、最小值。
(3)引入径向基核函数(RBF),通过调整g参数实现样本从低维空间到高维空间的映射,从而实现线性可分。

(4)使用二度Grid Search算法进行SV M模型训练及C&g参数寻优。
粗略搜索阶段 定义初始网格,设置大步距,获得局部最优参数区间;
精确搜索阶段 以最优参数组为搜索中心,设置小步距,不断扩大搜索范围,逐步跳出局部最优,获得全局最优解,从而实现分类效果最优。
3 试验结果与分析
(1)试验数据来自于某大型服装企业平台,试验共采用169组量体数据与版型之间的对应数据,随机选取131个样本作为训练集,38个样本作为测试集,见表2。
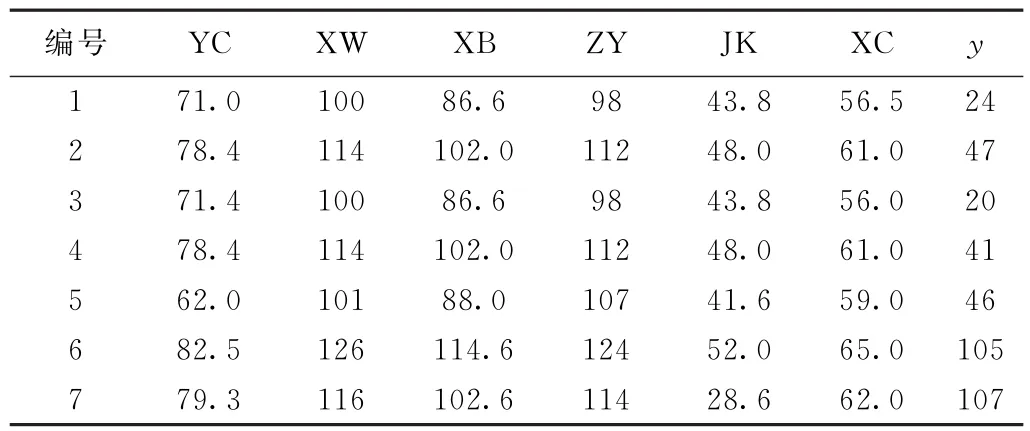
表2 量体数据版型数据集(上衣部分示例)
(2)首先设定所要搜索的(C,g)参数的初始网格搜索范围及初始步长,其中,C&g的初始网格搜索范围为[2-10,210],初始步长为4.5,通过交叉验证方法获得局部最优参数组;
(3)在其附近进行小范围的精确网格搜索,其C的网格搜索范围为[2-2,24],g的网格搜索范围为[2-4,24],其搜索步长为0.05;
(4)将最终得到的参数(C,g)重新传入到支持向量机的和函数中,建立基于二度网格搜索的支持向量机模型。
试验结果如图2所示。
从试验结果看出,将Grid Search-SVM算法运用于服装版型的预测分类研究中,有良好的分类效果,且将Grid Search网格搜索算法分步搜索,可大大缩短参数寻优时间,本次试验运行时间为4.47 s,最佳C参数为36.7,g参数为1.3,最终试验的版型分类准确率在90%以上,收敛情况好时可达到100%。
4 结语
为挖掘量体数据与服装版型的关系,构造出量体数据及服装版型之间的SV M数据模型,并通过Matlab进行仿真试验,使用SV M算法进行模型训练及模型验证,实现分类效果,并通过Grid Search二度网格搜索算法进行参数寻优,使准确率达到理想状态。量体数据及版型的预测研究实现了在服装定制推荐过程中根据量体数据进行版型推荐的过程,使得服装定制推荐的过程向前推进,逐步实现服装定制元素的推荐。针对量体数据及版型的研究对服装定制推荐有重要的理论与实践意义。

图2 试验结果
