平纹织物结构的三维仿真

张 卓，严玉蓉，杨声强，任忠海，*

(1.广州海关技术中心，广东 广州，510623;2.华南理工大学 材料科学与工程学院，广东 广州，510641;3.美国UL(深圳)安全试验所，广东 深圳，518047)

0 前言

Matlab是Mat h wor ks公司于20世纪80年代推出的数值计算软件，运用以矩阵运算为基础的程序语言，它有非常强大的数值计算能力，数域可扩展到复数[1]。快速且精确地绘制各种复杂的三维、不规则公式曲线或曲面是Matlab的长项，面向分析运算是其广泛应用于工程技术的主要原因。Matlab把所有点的坐标数据储存在二维或三维矩阵中，因此绘制图形时很容易就能控制图形的精度，而且这些坐标数据经过处理后还可移植、扩充到其他绘图软件中。

在建立复杂不规则三维模型时，Auto CAD绘制方法繁琐且误差很大[2];Open GL因为自身缺乏复杂三维形体函数而必须提取其他绘图软件建好的三维模型数据才能进行进一步图形处理[3];3d Max则是通过修改堆栈命令加工得到目标模型，是一款偏向商业影视娱乐、多媒体制作的软件。因此，选择了Matlab为织物结构的三维建模软件。

织物结构的仿真模型研究始于20世纪20年代，逐步从二维平面建模过渡到三维空间建模及质感模拟，目前国内外对织物结构仿真依据的理论主要分为Pierce模型法、分段函数法和样条曲线法[4]。

马维[5]使用Open GL结合VC++语言建立了平纹、斜纹等梭织物的三维模型，纱线截面假定为椭圆;谷大鹏等[6]用Matlab建立了平纹织物的三维模型，但纱线截面假设为圆形;朱生群等[4]使用Tex Gen建立了筒状纬编针织物的结构模型，假设纱线截面为圆形，使用B样条拟合理论建立模型。这些研究文献将织物中的纱线横截面假设为圆形显然有悖于真实的织物形态;另外，文献在建模时对纱线和织物的数学特征没有必要的假设条件，而且仅对纱线进行曲线拟合，缺乏对纱线曲面成型的理论推导。

1 平纹织物三维仿真模型的建立

图1是本文建立的平纹织物三维仿真模型，图例显示从2个不同方向观察同一模型。

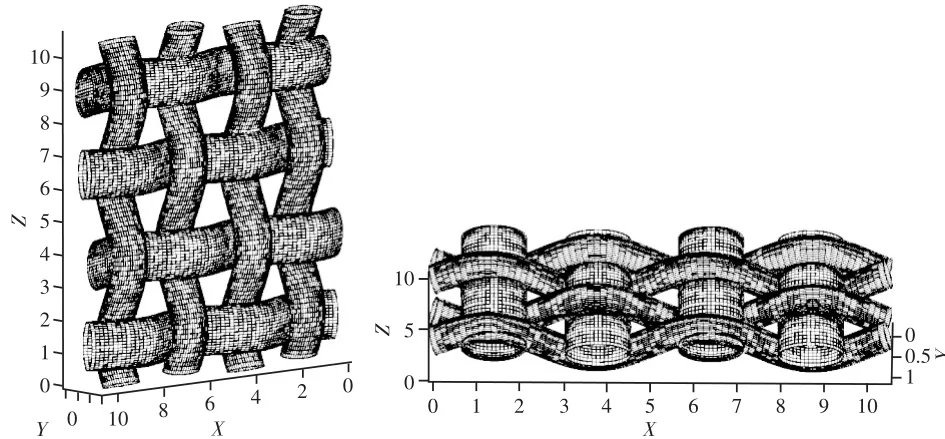
图1 平纹织物结构三维仿真效果

1.1 建立坐标系

按右手法则建立各坐标系：

(1)以纱线长度方向的中心轴线方向为Zl轴，横截面为XlOlYl面，建立纱线局部坐标系(下标l表示局部坐标系，下同);

(2)以织物厚度方向为Z轴，织物交织平面为XOY面，建立全局坐标系。

1.2 模型建立

1.2.1 假设条件[7-8]

在Peirce改进的梭织物模型中，假定纱线的横截面均为椭圆形，纱线既无伸长也无压缩变形，经纬纱交织附近相互包覆屈曲的地方为圆弧状，其余部分为直线段。

对于大多数织物，纱线由于挤压产生形变或有部分重叠现象出现不易进行仿真，但对于平纹类织物经大量切片实验研究得知，纱线的形态走势类似于正弦曲线，且不存在重叠现象，故以纱线屈曲形态为空间正弦或余弦曲线为例进行织物结构三维仿真[9]。

(1)纱线的横截面为椭圆形;

(2)纤维在纱线中排列紧密、均匀;

(3)纱线中所有弧线为三阶连续可微曲线，参数增加的方向为曲线的正向;

(4)纱线中所有弧线为正则曲线;

(5)纱线之间彼此密实接触，即纱线间无空隙;

(6)纱线表面光滑、平整，均没有变形;

(7)忽略经纱与纬纱交织点处的作用力，如摩擦、挤压或弯曲;

(8)单层织物中，经纬纱所在的上下2个平面互相平行;

(9)单层织物中，所有经纱或纬纱均分别排列在同一直线上。

1.2.2 纱线表面各点的坐标值计算

根据纱线几何体的形成原理，纱线长度方向中心线上任意一点的法平面与纱线曲面的交线都是一个椭圆。假设该椭圆的长短轴分别为a、b，如图2所示，纱线局部坐标系为XlOlYl，椭圆中心是Ol。

全局坐标系下的纱线空间模型如图3所示。观察方向与椭圆所在平面垂直，即与法线n的方向相反但平行。

图3中，Γ是纱线长度方向的中心线，为一C3类空间曲线。T、N、B分别是该曲线上任意一点的切向量、主法向量和副法向量。向量n是椭圆Ol所在平面的法线，且与3个坐标轴的欧拉角在[0，π]内变化。

局部坐标系下Γ应满足下列方程：

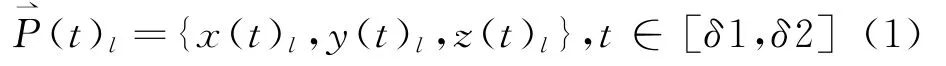
其中t为曲线Γ的参数，δ是取值区间。点Ol的单位主法向量β(t)为[10]：

点Ol的单位副法向量γt()为：

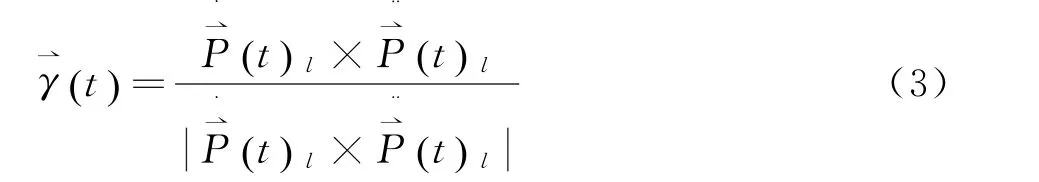
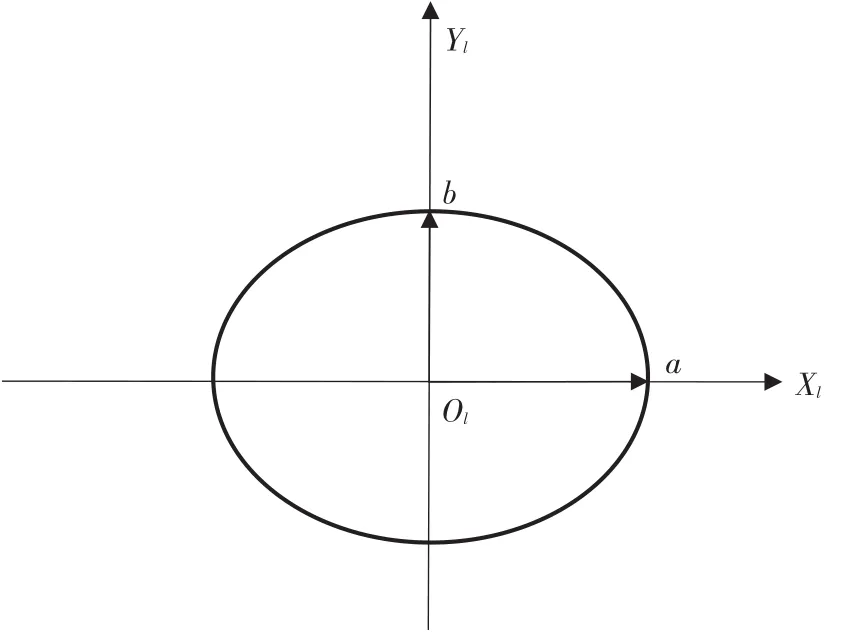
图2 局部坐标系下的纱线横截面模型

图3 全局坐标系下的纱线空间模型

另一方面，纱线可以看作由离散点构成的空间曲面，则椭圆Ol上的点就是这些离散点的一个子集。令椭圆Ol在局部坐标系XlOlYl的方程为：

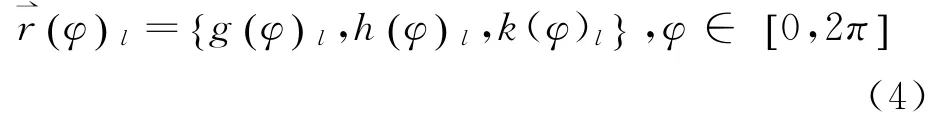
φ是椭圆上任意一点逆时针方向与Xl轴的夹角。

局部坐标系下将曲线Γ和椭圆r(φ)l进行运动A的变换就能得到全局坐标系下的曲线公式[11]：

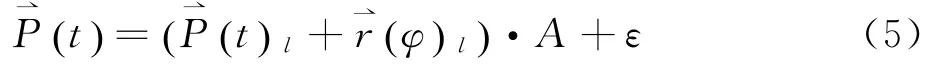
其中，A是方向余弦矩阵，ε是一空间向量，且ε∈R3。

由空间参数曲线的几何不变性原理，经过坐标系的复合运动后，曲线的各阶导矢是不变量。所以曲线Pt()l与椭圆r(φ)l经过位置变换后只存在坐标变化的差别。

假定椭圆Ol的法向量n的方向向上为正，结合式(6)，n的方向余弦ω，δ，ε可按下式计算：

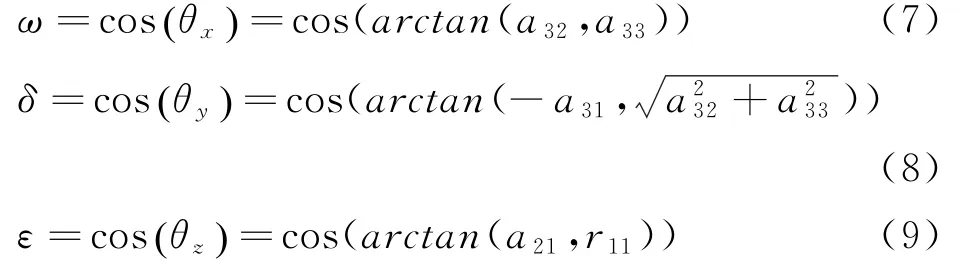
其中，θx、θy、θz为法向量n的欧拉角。

综合式(1)～式(9)，得到全局坐标系XYZ下的纱线表面任意点的坐标值：

T是从局部坐标系到全局坐标系的变换矩阵，矩阵元素下标y表示纱线。

至此，已经建立了纱线的表面各点坐标方程。

1.3 平纹织物结构模型

平纹织物的宏观结构是多条具有正弦或余弦曲线特征的纱线互相交织而成。如果将纱线表面离散成n个空间内的点，结合式(11)，则织物表面各点的坐标可表示成如下n×(n+1)齐次矩阵：

式(12)就是织物表面的点的坐标值，也即织物的三维结构模型。矩阵元素下标f表示织物。

最后，依据织物实际的规格，输入纱线的直径、屈曲角度、纱线间隔距离、经纬密度等参数，就能得到大小、形态可控的结构模型。

2 用Matlab实现平纹织物结构仿真

平纹织物仿真模型的编程流程如图4所示。

图4 平纹织物三维仿真模型的流程

当得到织物表面所有离散点的坐标值后，通过调用Matlab中的mesh或者surf函数，绘制织物表面曲面，即可实现织物的三维模型可视化，如图5所示。

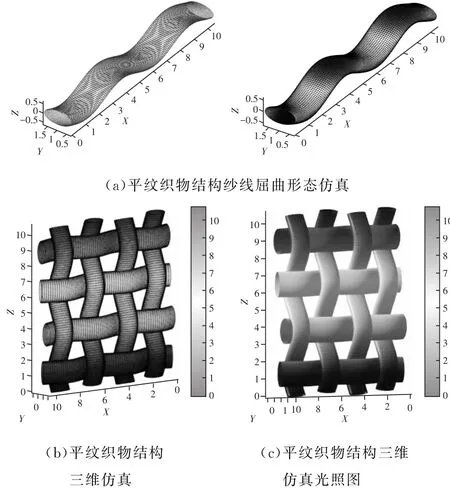
图5 纱线及织物三维仿真模型

其中图5(a)是调用不同的函数绘制的纱线模型，图5(b)是平纹织物三维仿真模型，图5(c)是进行光照处理后得到的模型。

3 结论

(1)平纹织物三维仿真模型真实反映了纱线的形状、大小和在织物结构中的相对位置，不仅是分析研究平纹织物结构的基础，而且也为研究平纹织物的力学过程、应力应变关系以及纱线间的相互作用机理打下了良好基础。

(2)在Matlab环境下的可视化编程，具有很大的优越性。计算效率高，数据可视化简单，为将来扩展不同结构的织物性能预测和检验模型的正确性提供了数学保证，也为后续其他类型的织物宏观物理性能的仿真研究提供了可靠的示范。

(3)使用Matlab建立织物三维仿真模型涉及数学、物理、计算机图形学和向量几何等多学科知识，因此覆盖面广、解决途径复杂。也正因为此，每一位研究者使用的方法都不尽相同，所以最终得到的模型精度、可扩展性差异较大。