一种基于层次聚类的空间非合作目标重构方法

朱昂帆， 杨佳琪， 王 立

0 引 言

由激光雷达生成的点云可以精确表示真实对象的三维信息，并且这种表示方式已广泛用于许多领域[1-2]，例如计算机视觉、计算机图形学.从点云进行三维重建的一般过程涉及网格生成和表面渲染.但是，三维重建的精度通常受点分布不均匀的影响，这通常是由于设备缺陷，人为和环境干扰所造成的.尤其是在扫描结构复杂的物体时，这种现象更加明显.此外，原始点云中的冗余点可能会导致重建的表面上产生孔洞并带来更高的计算量.因此，对于高质量的点云三维重建，处理这种分布不规则的点集是非常有必要的.

目前，已经有许多针对点云采样点的研究.早期的研究主要是简单地移除重叠区域的点.在文献[3]中，作者用一个新的点来替换点云中原有的两个点从而保证均匀的采样分布.这类方法用新的点来替代原始点云中的冗余点或者直接将其去掉.另外一种策略是将点云划分为许多网格单元，并用一种统一的表达形式来替代网格单元中的所有点，例如文献[4].这类方法大多是基于八叉树.这种通过空间分解的采样方法可以更加方便快捷地控制采样规模.

基于上述考虑，本文提出了一种新颖的基于全局约束的局部层次聚类的点云采样方法.该方法用于处理非均匀点云数据，从而实现高质量的三维重建.该方法同样也是基于八叉树.与先前的工作主要区别在于：该方法仅对网格单元中的冗余点进行重新采样，并且综合考虑点云的全局约束条件，使采样比例适应于点云的整体尺寸大小.为了降低传统聚类算法的计算复杂度，使用了三维空间分解的方法，随后对局部点集(即空间分解后每个网格单元中的点)进行分层聚类，以提高图像的一致性.图1比较了本文所使用的方法处理之前和之后的三维重建质量.

图1 采用层次聚类算法前后的点云分布对比结果Fig.1 Comparison results of point cloud distribution before andafter using hierarchical clustering algorithm

文章的剩余部分由以下章节构成.第2节详细介绍了本文所提出的方法，包括3D空间分解和层次聚类.第三部分介绍了本文所使用的方法在真实世界扫描点云上的验证实验.第四部分得出本文的结论.

1 方 法

本章节将详细讲解本文所采用的局部层次聚类方法.该方法由两部分构成：1.基于自适应八叉树的三维空间分解，2.层次聚类.前者将整个点云分解为一系列体素，从而加速整个计算过程；后者则对每个体素内的点进行处理，完成点云重构.

1.1 基于自适应八叉树的三维空间分解

基于八叉树的空间分解的概念如下.令C为输入点云，O为其三维边界框.本文将O分解为许多小的网格单元，并称之为体素[5].八叉树由这些体素构成并且点云C中的点被均匀的拆分到这n×n×n个体素当中.八叉树的构建过程如图2所示，其中l代表每个体素v的边长.

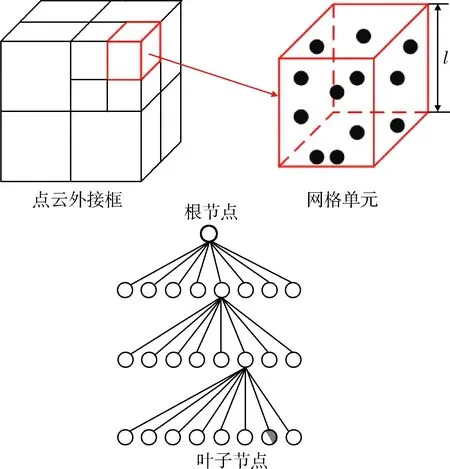
图2 基于八叉树的三维空间分解Fig.2 3D space decomposition based on octree

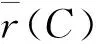
对于一给定的点云C，首先计算出其外接框的最大坐标ptmax=[xmaxymaxzmax]与最小坐标ptmin=[xminyminzmin],然后求出最大最小坐标之间的距离D：

(1)

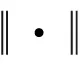
l=φ×D

(2)

其中φ是一个可变的参数，在本文中φ设为0.01为一个比较合适的范围.

通过这样一种自适应的方式，使得每个体素的边长可以随着目标尺寸的变化而变化，并且不会受到点云密度的影响.这在一定程度上也提高了算法的鲁棒性.

1.2 层次聚类

当八叉树构建完成后，点云C中的点就会分布在不同的体素当中.给定一个具有m个点的体素v，本文希望的是将这些点分配到c个簇当中.首先，将所有的m个点分为m个簇(即一个簇包含一个点).然后，以迭代的方式将两个选定的点组合为一个簇.令ci为体素v在第i次迭代中簇的数量，如果没有任何预设的迭代停止条件，则整个迭代过程将一直持续到ci=1为止，即所有点已经合并到一个簇当中.通常，可以使用一个距离约束来控制每个体素中的簇数.令D1和D2构成了体素v中的一个簇对，则簇对之间的距离定义为：

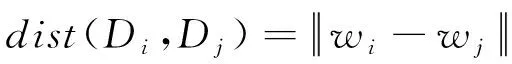
(3)

其中，wi是簇Di的中心.然后通过如下公式来获得当前迭代过程中距离最近的簇对D′和D″:

(D′,D″)=argmindist(Di,Dj)

(4)

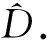
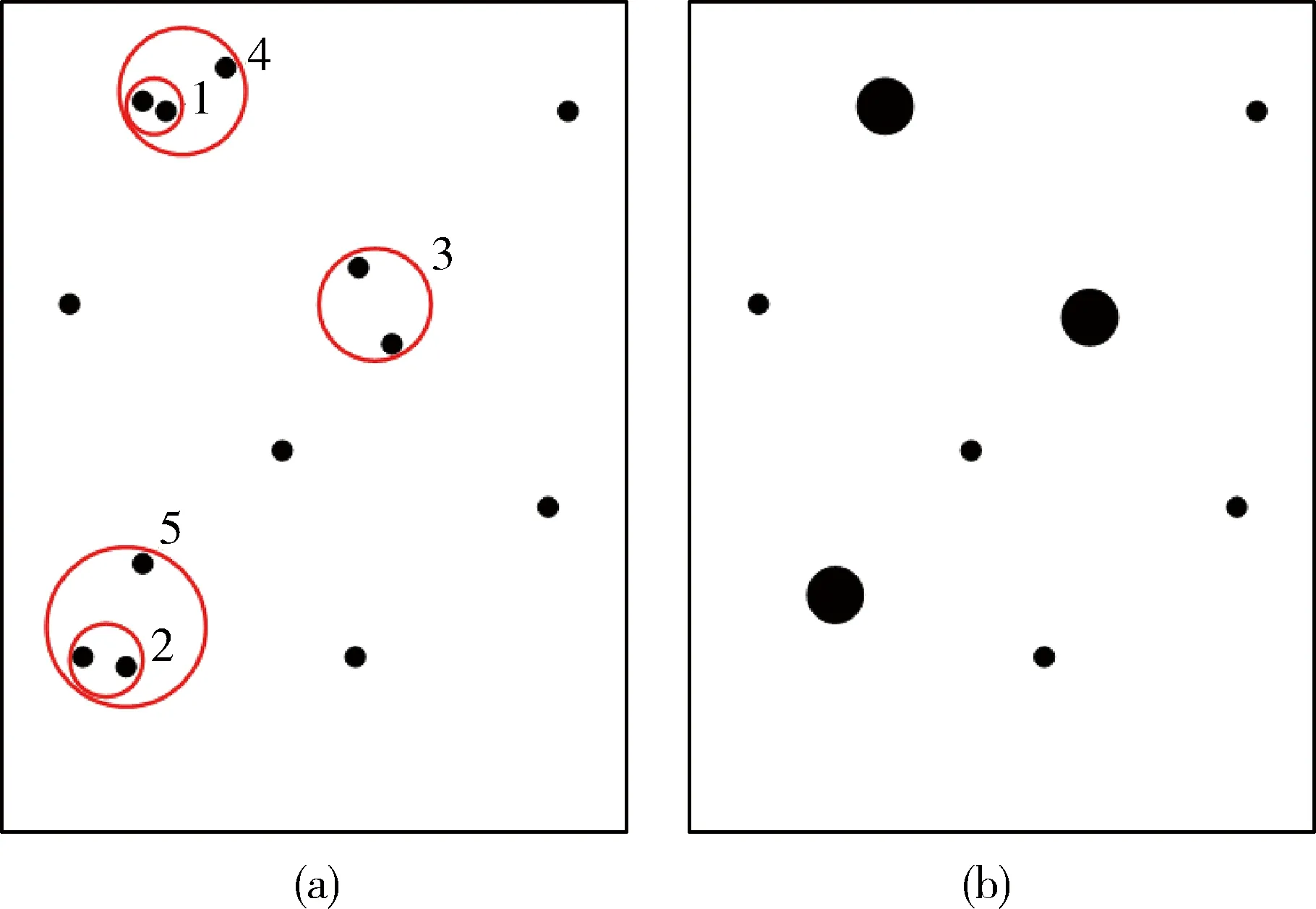
图3 二维空间中的局部层次聚类示意图.Fig.3 Illustration of local hierarchical clustering in 2D space.

dc的大小决定了分层聚类后体素v的密度.为了克服点云密度的影响，采用如下公式来计算dc

dc=β×D

(5)

其中，β是一个常数，本文中，β设为0.005.

在通过上述方式对点云进行层次聚类后，使用文献[7]所提出的方法来完成后续的点云重建.

2 实 验

在本节中，本文进行了一系列实验来验证局部层次聚类方法在非合作目标上的有效性.接下来，本文将分别展示实验数据、评价指标、比较方法、视觉效果以及定量结果.本文所采用的方法在VS2015、OpenGL和PCL[8]的基础上实现.所有实验均在具有8 GB RAM的3.5 GHz Intel(R)Core 3处理器上进行.

2.1 实验数据与评价指标

本文将三个非合作目标的点云模型做为实验数据.初始的模型不含任何噪声，本文将其作为实验真值.然后，通过人为干预的方式使其点分布不均匀，从而作为本实验的测试数据.重构误差err(C,Cgt)的定义如下:

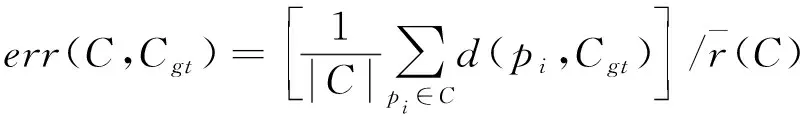
(6)

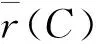
本文的评价准则是计算采样所得到的点云模型C与真值模型Cgt之间的重构误差.然而，点云的密度会对重构误差的计算产生较大的影响.因此，在文献[9]的基础上，本文使用重构误差除以点云的平均密度作为最终的评价指标，从而保证能够公平地比较不同密度的点云.

2.2 性能比较

本文使用文献[4]所提出的采样方法(US)和文献[6]所提出的采样方法(LHC)作为比较的基准.图4和表1展示了两种方法在非合作目标数据集上的重建结果.从实验结果中可以看到，无论是视觉感受还是定量比较，本文所提出的方法要优于文献[4]和文献[6]所提出的方法.可以在测试数据上发现很多孔洞，这些孔洞则是由于点的不均匀分布导致的.我们所采用的方法则可以得到更多均匀分布的三角表面并保留更多的几何特征.本文的重建误差也更小，这表明了基于全局约束的局部层次聚类方法的有效性.

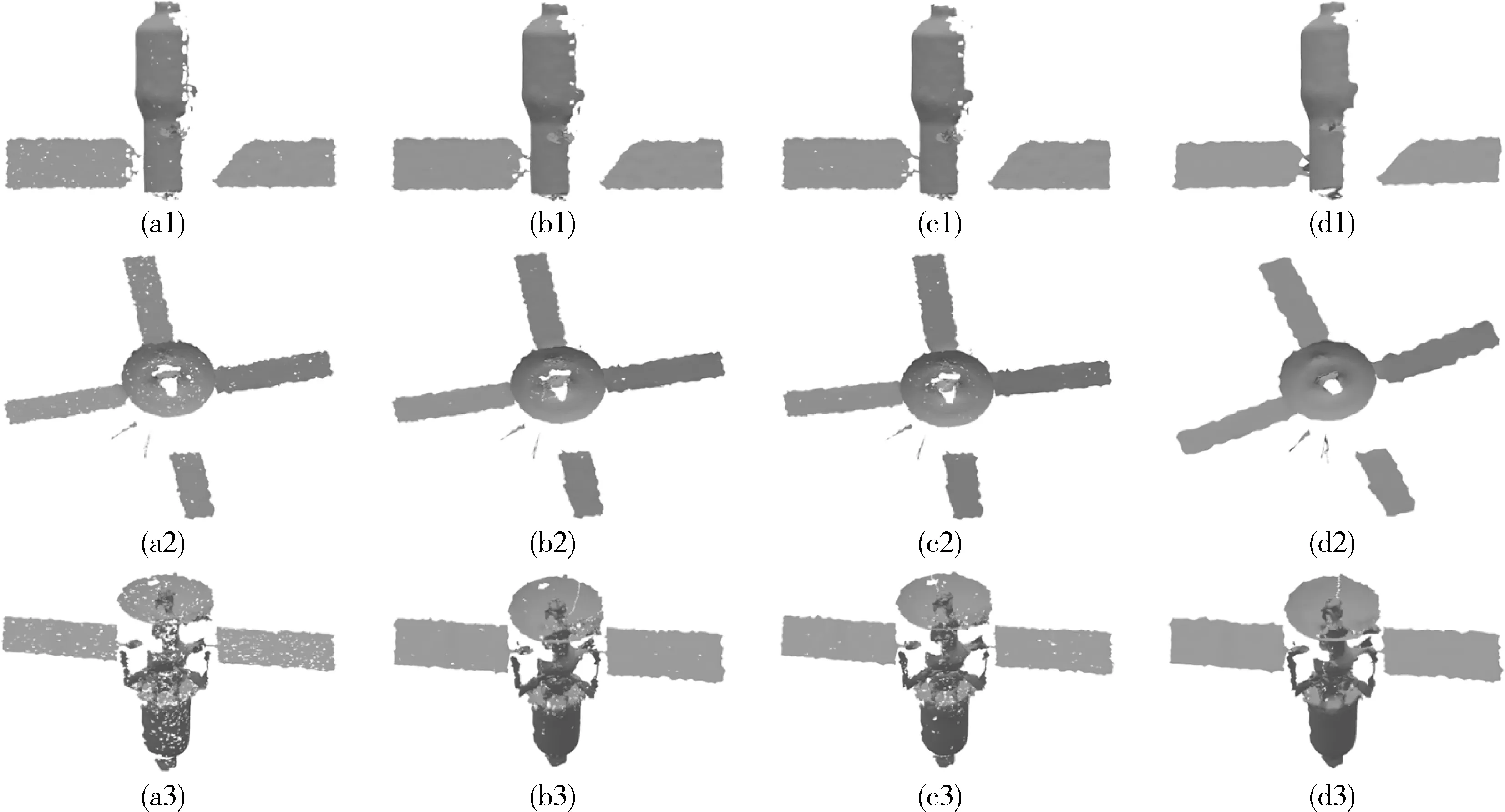
图4 性能比较示意图Fig.4 Visualization of performance comparison.

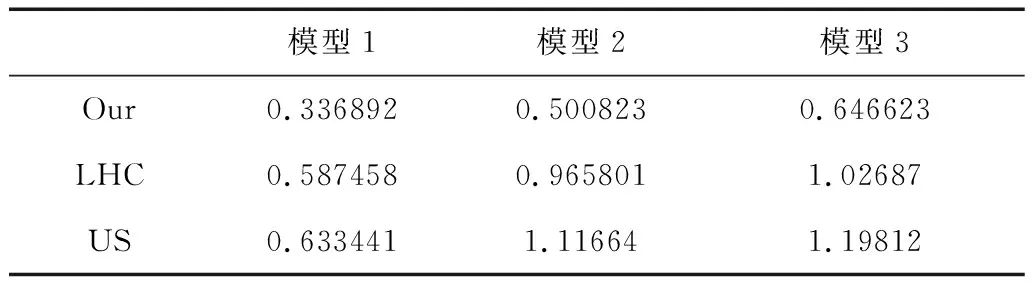
表1 3种方法的定量化性能比较Tab.1 Quantitative performance comparison of three methods

3 结 论

本文提出了一种基于全局约束的局部层次聚类的非均匀点云三维重建方法.这种方法主要包括两个部分：1)基于自适应八叉树的空间分解；2)层次聚类.本文在非合作目标点云数据上验证了该方法的有效性.同时，与其他方法进行了比较，进一步显示了该方法的优越性.