在完善数学学科知识结构中获得深度理解
2020-04-27任卫兵
任卫兵

摘 要 数学教学中应清楚地认识到“知识的良好组织”的重要地位。在教学中,应重视比较,及时引导学生寻找知识之间的联系,促进学生对数学知识的整体理解;通过题组,进行有效关联,拓展延伸形成知识的组块,实现知识结构内部的双向循环;拓展学生对重要概念、核心知识的深度理解,提升学生的思维水平和认知水平。
关键词 结构 理解 整体 联系
认知结构的形成与理解过程是一个双向互动的过程。理解是一个动态的有层次性的学习过程。在小学数学教学中,要让学生能够用联系的思维,把握知识之间的结构,促进理解层次向高级发展,从而发展学生的思维能力与认知水平。促进深度理解的认知结构的形成,除了在新授内容时须要聚焦核心、进行有效的线性串联外,在各种知识整理学习中,更要积极构建知识图谱。即使如此,在知识建构过程中必定还存在着一些断点、断层,对作为知识结构关键的核心概念,还存在深入理解的空间,基本的数学思想方法还有进行序列延伸拓展的必要。因此,在教学中,要积极组织教学内容,整体设计,及时填补学生认知结构中的空白,打通知识之间的有效联系,在完善数学学科知识结构的过程中,促进理解,培养学生数学素养。
一、完善内容结构,促进整体理解
新知识的理解是指新知识能被成功地纳入到主体已有的“概念网络”中,也即与主体已有的知识和经验建立起广泛的联系。教材中的编排呈现出螺旋递进上升的特点,而分课时的教学会让知识的整体性与联系性变得脆弱而隐蔽,有些例题之间在意义上有重大关联,但教学时要分课时进行教学。如果在单元教学之后进行整理,就失去了形成结构的最佳时机,对后续学习产生负面影响。因此在教学中,要及时主动构建知识之间的联系,在比较关联中强化新旧知识之间的联系,完善学科知识结构,促进对知识的整体理解。
如苏教版《数学》六年级上册“分数乘法”中,简单的分数乘法的实际问题,分两课时教学,教材编排如下。
不难看出,第二、三课时教学的都是简单的分数乘法的实际问题。第一课时是整数乘法意义“求几个相同加数和的简便运算”的迁移,而“求一个数的几分之几是多少”则是整数乘法中“求一个数的几倍是多少”的拓展。如果学生没有自行将知识连接,缺少反思的意识与能力,新知识便容易形成知识的“孤岛”,阻断了知识之间的联系,也就意味着理解的浅尝辄止。而这两课的教学各自都有着教学的重点与难点,如第三课时的教学,重点放在理解关键句“红花比黄花多”的意义上,新授时无暇顾及沟通与联系。因此,教学中须要利用机动课时,进行沟通。
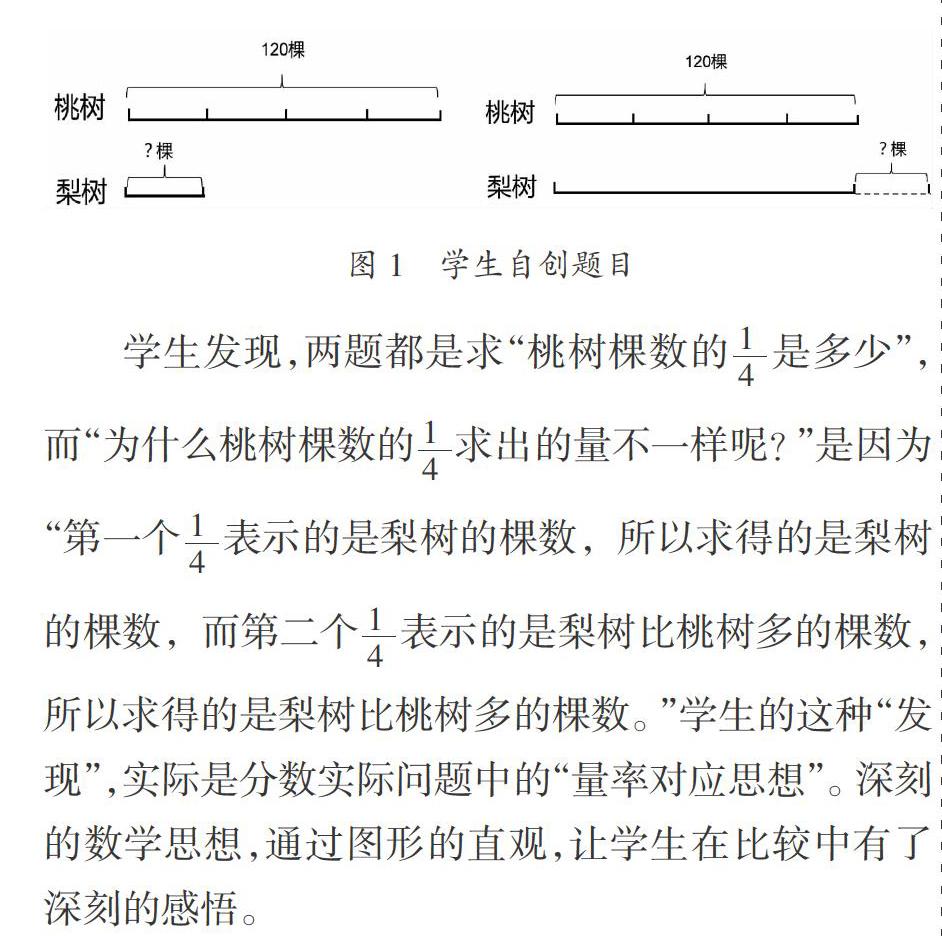
通过学生自创题目,画出相应的线段图(图1)。教师重点引导学生比较相同点与不同点。
学生发现,两题都是求“桃树棵数的是多少”,而“为什么桃树棵数的求出的量不一样呢?”是因为“第一个表示的是梨树的棵数,所以求得的是梨树的棵数,而第二个表示的是梨树比桃树多的棵数,所以求得的是梨树比桃树多的棵数。”学生的这种“发现”,实际是分数实际问题中的“量率对应思想”。深刻的数学思想,通过图形的直观,让学生在比较中有了深刻的感悟。
教学中这些知识点之间局部的联系,不同于整个单元、整册知识的整体框架,如果不及时沟通与联系,局部组织不循环,容易形成对理解的阻碍。通过对知识的多元表征,寻找共同之处,是形成知识结构的常用方法。沟通新旧知识之间的联系,利用旧知进行有效迁移,促进对新知识的理解,则是教学结构内化为认知结构的常规路径。
二、扩张知识结构,促进结构理解
数学中一些重要知识点、数学思想方法,具有生长性,但在进行单元整理时,由于无法与整个知识网构成一体,往往处于孤立状态。教学中,可将这些知识点或某种数学思想方法,通过题组进行线性的或是发散性的拓展,扩张知识的版图,将散点串线织网,向纵深发展,形成“知识包”或“方法链”。在此形成知识的组织结构中,强化学生的联系思维、发散思维、创造思维等,提升知识的可迁移性。
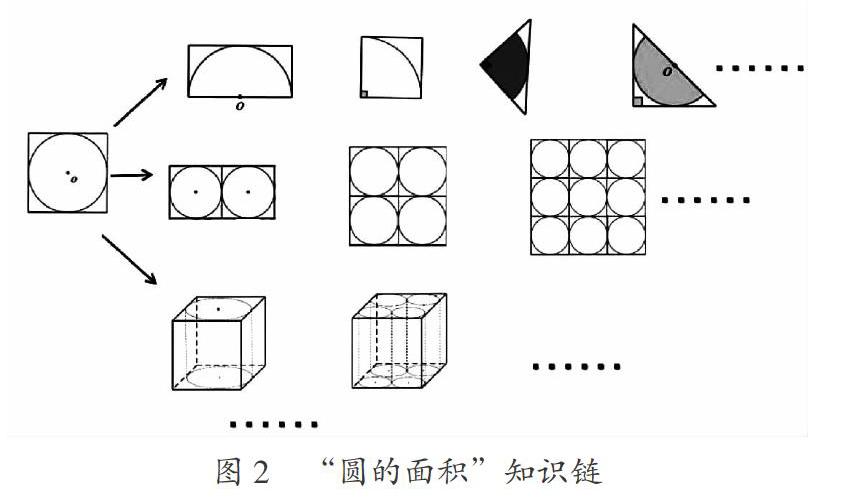
如苏教版《数学》五年级下册“圆的面积”教学之后,经常有“圆的外切正方形与圆”“圆的内接正方形与圆”之类的实际问题。教学这种类型的实际问题,通过切割转换,学生当时是能理解的,但过后的遗忘率相当高,这是因为知识、方法没有形成相应的结构。如果在教学时通过主动关联,进行联想,将相关知识联系起来,综合运用商不变规律、比的基本性质,获取知识之间的内在联系,不断扩展知识的版图。此时整体及部分互为理解的背景经验,不仅可以帮助学生知道相关知识是一个有联系的整体,而且知道整体是如何形成的,内部是如何关联的,这样才能产生超越知识的力量,最终扩展成如下知识链(图2)。
由一到多,不仅仅是这一题到多题,而是让学生进一步体会用联系的观点去学习数学,主动構建数学知识之间联系的一种意识与能力。“要对知识形成深刻的、真正的理解,这意味着学习者所获得的知识是结构化的、整合的。”着眼整体进行教学设计,着力关系构建知识体系,着重体验形成结构化的思维方式与知识网络,发挥知识之间联系的力量、整体的系统教学的力量。
深度挖掘知识、题目之间的渊源,能使相对独立的数学内容变得更为丰富、立体。在这方面,现行教材中的素材“俯拾皆是”。如在教学圆柱、圆锥之后,教材中分别编排了旋转长方形与直角三角形的习题。这些相关联的习题,可以以主题研究的形式,进行整体设计。例如可以组织以“旋转”为主题的拓展:直角三角形以斜边为轴,旋转一周,能够形成什么样的图形?如何求这个图形的体积?通过探究,引导学生发现关键在于旋转半径与旋转轴这两个要素,它们会影响旋转形成的立体图形的体积。由于旋转半径与旋转轴互相垂直,因而以斜边为轴旋转形成的立体图形体积就是两个底面相同(因为旋转半径相同),高之和为斜边的两个圆锥的体积之和。接着以平行四边形的任意一边为轴,旋转平行四边形,如图3。通过画图,找出旋转半径——平行四边形的高,将旋转之后形成的图形画出来,并进行转化,转化为一个长方形旋转之后形成的图形。还可引导学生继续拓展至其他的图形旋转,将课堂学习引向课外的自主探索。这样,以一个主题串联,以相同的方法,深入研究。在此过程中,学生的空间观念及其他的数学能力素养都得到了发展。
三、丰富核心概念,促进深入理解
数学概念有层次性、多维度的特点。对核心概念的深入理解,可以加强知识结构的稳固性,将思维、认知水平上升至一个新的台阶,提升学生的数学化水平。如2、3、5的倍数的认识,有必要让学生突破以末位数去判断的“表层结构”,去寻找知识内在统一的“深层结构”,从而加深理解,形成统一的认知结构。
如分数的认识,经历了意义、解决实际问题、比等相互影响、互相促进的一个循环过程,已有了较为完善的认知结构。但部分学生对分数,还一直处于过程的、操作的层面,并未凝聚至对象的、抽象的高级思维水平。如解决“工程问题”,学生都是用具体数量去解答的,而不能将工作总量看作“单位1”。固然,教材并没有编排这一内容的教学。但我们不应否认,工程问题教学不仅可以加深对分数意义的理解,还可以培养学生的抽象思维能力、建模能力。以下是工程问题教学的几个教学环节:
1.通过具体数量计算:有18吨石灰,如果大车独运,要4次运完;如果小车独运,要12次运完。两车合运,几次可以运完?
2.改变工作总量,引发猜想,并运用直观图联系商不变规律解释。初步发现总量的变化与工作效率之和变化之间的关系。通过直观图(图4),激活已有知识体系中的商不变规律、分数的基本性质等知识,引发学生继续向深处探究。
3.验证猜想,概括抽象。与总量无关,就把总量这个条件去掉,如何解决?
4.借助字母,构建算法。引导学生用字母表示:总数为a吨的话,a÷(a÷4+a÷12),结合图与算式的直观,把a提取出来,得1÷(+)=3次。
根据算式结合直观图,理解“单位1”,脱离具体量,运用分率列出算式。
5.变换情境,建立模型。解答购物、行程等情境中的问题,并比较:这些问题在解答过程中有什么共同之处?再根据算式“1÷(+)”编一个故事。
在以上教学中,着力去抽象理解“单位1”,建立工程问题的模型,提高解决实际问题的能力。一是在不同情境下把总数看作单位“1”,由多种情境,建立模型;二是由一到多,由模型到情境的回归。“只有经常变换课题的具体情境,在不同的情境中展现同一结构关系,学生才不会被具体情境所迷惑。”对小学数学学科来说,不仅要学习如何数学化、抽象化,也要让学生有大量的机会去体会如何解释、如何猜测、如何变式、如何拓展,而这才是真实、完整的数学学习生活。
作为小学数学教师,要注意對数学学习素材进行再整合、再建设,设计、生成更具张力的数学大问题;要注意把学生真正置于课堂中央,让他们自行组织信息,自主发现问题、分析问题和解决问题;要注意将深化教学结构与促进学生理解有机结合起来,将自下而上的学习过程(搭建组块)与自上而下的学习过程(纵览全局)综合起来,使培养高阶思维、提升数学素养的目标能够在课堂上真正得以落实。
参考文献
[1] 黄玉香.着眼素养培育的结构化教学[J].福建教育,2019(06).
[2] 波利亚.数学的发现[M].刘景麟.曹之江.邹清莲,译.呼和浩特:内蒙古人民出版社,1981.
[责任编辑:陈国庆]
