建筑塔式起重机的故障分析和结构改进方法
2020-04-27肖辉李超杨代云
肖辉 李超 杨代云


摘 要
为解决某型号塔式起重机平衡臂结构开裂失效故障,研究分析建立了一种以有限元模型分析和解决故障的方法。分析发现现有平衡臂结构变形和应变过大是导致故障的原因,平衡臂结构改进后两种极限工况下的变形和应力分别减少了84.5%、43.2%和86.1%、86%,得到了一种可提高平衡臂使用寿命、降低故障率的结构改进方案,从而达到高效诊断故障和解决故障的目的,为塔式起重机结构设计和故障诊断提供了一种高效的计算方法。
关键词
塔式起重机;平衡臂;极限工况;故障诊断
中图分类号: P313.1 文獻标识码: A
DOI:10.19694/j.cnki.issn2095-2457.2020.05.045
0 引言
塔式结构的起重机广泛用于我国建筑行业中,配合变幅小车以及回转台,能在以规定的最大起重幅度和最高起吊高度构成的圆柱空间内快速转运重物[1]。塔式起重机主要由动力部分,控制部分和金属结构部分组成。金属结构是塔式起重机承受负载的承重金属框架,由多种截面形状的连杆焊接而成,包括:塔身,塔帽,起重臂,平衡臂,拉索等,如图1所示。塔身由多个标准节通过螺栓固接,塔身与底座固接,根据实际使用要求,底座与地面有固定式和移动式等连接方式。塔帽与塔身之间通过回转台连接,可实现起重臂回转起吊不同方向的重物的功能。起重臂和平衡臂分别通过螺栓固接在塔帽两侧,并通过拉索与塔尖连接。塔式起重机变幅起吊过程中,各金属杆件连续承受随机变化的拉压载荷以及力矩作用。实践证明,塔式起重机金属结构失效开裂、变形是最为常见的故障。
为解决某型号塔式起重机平衡臂变形和开裂问题,构建该机型的有限元模型,通过对比结构改进前后有限元分析结果,为解决该机型变形和开裂问题提供了分析依据。
1 建立有限元模型
1.1 搭建三维模
塔式起重机金属构件按照功能可分为:塔身、回转台、塔帽、起重臂、平衡臂、拉索等,由不同截面形状的冷拔钢杆件组成。塔身标准节以及塔帽由4根立柱以及焊接在立柱间的斜拉杆构成,起重臂以及平衡臂由上下弦杆以及之间的斜拉杆构成,拉索为圆钢制成的连杆连接而成[2]。表1所示为组成该机型的各金属杆件的截面参数。
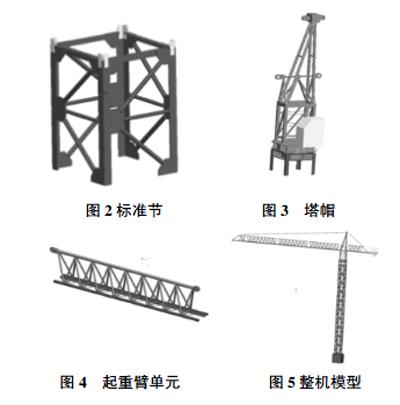
根据表1所示截面形状,基于Pro/e建立的该型号塔式起重机三维模型:10节标准节通过螺栓连接构成塔身,单节塔身标准节高度3M,塔身总体高度30M。3节起重臂单元通过螺栓连接构成起重臂,单节起重臂单元长度15M,起重臂总体长度45M。平衡臂长11M,末端放置配重。如图2-5所示。
1.2 建立有限元模型
1.2.1 模型简化分析
有限元模型简化遵循的原则:(1)为保证建模准确性,应保证有限元模型整体尺寸与实际尺寸一致;(2)为提高仿真效率,尺寸小,质量集中的结构,在不影响准确性的前提下,可对模型简化处理。(3)有限元模型可不体现控制部分、动力部分、变幅小车、配重块等结构外形特征,只需在相应安装位置施加力载荷进行等效替换[3]。
根据三维模型结构尺寸等特征参数,在ANSYS中设置好单位,确保有限元模型尺寸参数与实际尺寸参数一致。
金属结构除了框架,还包括回转台、驾驶室等结构。该部分结构质量集中,且尺寸远小于塔式起重机整体尺寸,在整机有限元模型中,可使用梁单元进行等效处理,保证模型准确可靠的前提下,避免具有不同节点的单元连接问题,提高建模以及计算效率。
钢丝绳质量和尺寸远小于塔机整机重量和尺寸,有限元模型中可忽略不计。用施加在变幅小车位置处竖直向下的作用力来等效处理起重负载。
用刚性连接建立约束关系表示塔式起重机各结构模块间的螺栓连接,限制相邻两构件螺栓连接处节点的6个自由度[4]。
1.2.2 单元及连接选择
基于TIMOSHENKO梁理论的3D线性有限应变梁单元BEAM188是一个具有二节点的三维线性梁,每节点具有6个自由度,适用于线性分析以及大偏转和大应力的非线性分析,并且能定义任何材料截面形状,适用于分析细长的梁杆机构[5]。塔身标准节、起重臂、平衡臂以及塔帽结构主要承受的负载为拉压力以及弯矩,表现出较大的静位移和应力,且组成杆件具有多种截面形状,具有不同的转动惯量。因此,该型号塔机采用BEAM188单元进行网格划分求解。
塔身标准节之间、塔身与塔帽之间以及塔帽与起重臂和平衡臂之间均为螺栓连接,限制了两组成构件重合部分的6个自由度,等效于刚性连接。在构建有限元模型时,采用简化的方法进行处理,使用刚性连接限制螺栓连接处的自由度[6]。
1.2.3 载荷简化
塔式起重机承受的载荷主要有负载重量、配重、动力和控制系统部分重量、塔机自重等。
该型号的塔式起重机塔身高度30M,起重臂长45M,起重性能为:起重机最大起重载荷为2t,配重质量2.8t,吊幅在18-32M的起重载荷均为2t,吊幅在35 M、40M和45M的起重载荷分别是1.68t、1.4t和1.3t。动力系统、控制系统以、操作手及塔身自重总重量2.5t,用作用在塔机质心处的载荷来等效该部分重量。该型号机型底座与地面为固定式,不可移动,因此,在有限元模型中需限制塔底座元素的所有自由度。
1.2.4 有限元计算和结果分析
塔机主要材料Q345B的屈服强度3.45×108 Pa,弹性模量206GPa,泊松比0.27,密度7850kg/m3,结合Pro/e三维模型、表1所有的塔机各主要结构的截面参数以及负载情况建立的有限元模型如图6-7所示。该模型由2442个单元,2169个节点组成。
为解决塔机金属构件的失效、开裂问题,需分析考虑极限工况下塔式起重机的变形和应力分布情况,塔式起重机极限工况有两种,一种是吊幅最小,起重质量最大,另一种是吊幅最大,起重质量最小。设定工况一为:吊幅18M,起重量2t;工况二为:吊幅45M,起重量1.3t。工况一、二的塔机配重和塔机自重均相同,分别为2.8t和2.5t。
在有限元模型上添加相应载荷,计算结果如图9 - 11所示。工況一和工况二的最大位移和最大应力位置均发生在平衡臂尾端,最大变形量分别为243mm和214mm,最大应力值分别为2.80×108Pa和2.79×108Pa。平衡臂尾端长时间在较大变形量的情况下,且连续承受配重以及来自拉索的变化负载作用,最先也最容易表现出失效和开裂。
通过计算结果可知:由于结构原因,该型号塔式起重机应力和变形最大位置均为安装配重的平衡臂上,且变形和应变值均较大,可以预测该类型塔式起重机平衡臂故障较多,这与实际使用当中表现的故障类型一致,验证了模型的有效可靠性。
2 塔机结构改进设计
2.1 结构改进方案
在平衡臂所受负载确定的情况下,通过结构改进,提高平衡臂整体的刚度和强度,达到减小平衡臂变形和应力集中的问题。图12所示为该平衡臂的原始结构简图,结构改进后的平衡臂结构如图13所示,通过增加斜拉杆达到提高平衡臂刚度和强度的目的。
2.2 结果对比分析
在保证所有载荷和约束不变的前提下,计算工况一和工况二下的最大变形和应力。结果表明:该种改进方法能够明显减小塔机变形:工况一的最大变形由结构改进前的243mm减小到结构改进后的34.6mm,减小了84.5%;最大应力由结构改进前的2.80×108Pa减小到结构改进后的0.39×108Pa,减小了86.1%。工况二的最大变形由结构改进前的213mm减小到结构改进后的121mm,减小了43.2%;最大应力由结构改进前的2.79×108Pa减小到结构改进后的0.39×108Pa,减小了86%。结果表明按照该种方式改进的平衡臂应变和应力情况均远小于结构改进前的情况,最大应力值远小于Q345B的屈服强度3.45×108 Pa,满足受力情况要求,可提高平衡臂的使用寿命,可减少故障的发生。
在有效可靠的有限元模型上进行的结构改进分析结果表明,该种结构方案不仅能验证和预测实际使用中出现的故障,还能为出现的实际故障提供解决方案,改进后的平衡臂结构符合安全使用的要求。
3 结论
通过有限元模型分析发现该种型号的塔机平衡臂在两种极限工况下较大的变形和应力是导致故障发生的原因所在,平衡臂连杆连接处的应力值已经达到2.80×108Pa,接近材料的屈服极限。在后期结构改进时应着重提高平衡臂结构的整体刚度和强度,降低其变形和局部应力。本研究的结论总结如下:
(1)通过与实际使用情况比对,分析和简化模型,建立了有效可靠的有限元模型。
(2)有限元模型分析发现塔机平衡臂结构原因是导致故障的主要原因,并提供了一种有效可靠的结构改进方法。
(3)建立在有限元模型上的结构改进设计方法,可以推广应用到塔机其他结构在设计阶段的故障的预测,可提高塔机故障检测和分析的效率。
参考文献
[1]于兰峰.塔式起重机结构刚性及动态优化研究[D].2006.
[2]符国炎.基于ANSYS的塔式起重机结构分析[J].设计计算,2019(5).
[3]沈荣胜,王胜春,王积永.基于Ansys的塔式起重机模态分析[J].起重运输机械, 2011(9).
[4]高崇文,田文磊.塔机多工况有限元分析并行求解的研究[J].机械设计与制造, 2019(3).
[5]李茂,李楠楠,孙端阳.塔机起重臂端部横梁撕裂原因分析及加固方法[J].建筑机械化,2019(10).
[6]于洪柱.基于ANSYS的平头塔机臂架结构静力分析[J].华电技术,2018 (11).
