无定河流域径流侵蚀功率时空变化特征

王 伟, 李占斌,2, 杨 瑞, 贾 路, 任宗萍, 李 鹏

(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室, 西安 710048; 2.中国科学院 水利部 水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室, 陕西 杨凌 712100; 3 延安大学 建筑工程学院, 陕西 延安 716000)

流域尺度上，径流不仅是泥沙的输移媒介，而且是能量传递、转化的纽带和载体。因此，径流侵蚀能量的传递过程、空间尺度效应及其与输沙之间的响应关系是流域侵蚀研究的薄弱环节，亟待对其进行定量研究[1]。研究人员[2]尝试采用径流能耗理论对侵蚀产沙过程进行了模拟和分析，得到了较好的结果。Yang C T[3]审查了常规泥沙输送方程推导中所用的基本假设，提出径流功率理论。同时为了进一步确定总含沙量，杨志达[4]提出了包括有关变量的函数关系。崔文滨等[5]应用这一理论对不同坡度和流量条件下的侵蚀产沙特征进行了分析和比较，发现径流功率理论能够较好地表征侵蚀产沙。以上研究说明，侵蚀能量理论能够较好的描述土壤侵蚀。尺度问题在流域水沙模拟中具有非常重要意义，不同时空尺度的水沙响应关系十分复杂，还需要科研人员不断地进行研究和探索。鲁克新等[6-7]基于次暴雨洪水过程中径流深、洪峰流量模数两个水文参数，提出了径流侵蚀功率的概念，表明径流侵蚀功率在次暴雨尺度可以更好地表征坡面和流域尺度的水力侵蚀动力。程圣东[8]首次提出了计算年功率、月功率的理论和计算方法。研究表明，在不同尺度坡面侵蚀产沙中，表明径流侵蚀功率与坡面次暴雨侵蚀模数之间存在极显著的幂函数相关关系，径流侵蚀功率可以较好地表征坡面次暴雨水力侵蚀动力[9]。

本文基于水蚀动力过程的径流侵蚀能量理论，将其运用至年尺度，首先采用Mann-Kendall法和线性回归法分析无定河流域1956—2010年年径流量和年径流侵蚀功率的时空变化规律；利用Mann-Kendall突变点检验，识别出径流的突变年份，对比分析突变年份前后的年径流侵蚀功率和年径流量的时空变化规律，并建立无定河流域不同空间尺度的年径流侵蚀功率—输沙相关模型。

1 研究区概况

无定河是黄河河口至龙门区间最大的支流，发源于陕西白于山(37°00′00″—39°0′0″N，107°47′48″—110°24′21″E)。无定河流域面积30 261 km2，流域干流全长491 km，主河道平均比降为1.97%，植被覆盖率低，垦殖指数高达60%，沟壑纵横，地形破碎、林木稀少，水土流失严重，为泥沙的主要来源区[10]。

2 数据和方法

2.1 数据来源与处理

本文所用的水文资料来源于黄河水文年鉴中1956—2010年的水文资料，选取无定河流域5个代表水文测站李家河站、绥德站、赵石窑站、丁家沟站和白家川站(图1)，各代表站分别控制小理河流域、大理河流域、无定河赵石窑站以上流域、无定河丁家沟站以上流域、无定河流域，控制流域面积分别为807 km2，3 893 km2，15 325 km2，23 422 km2，29 662 km2。

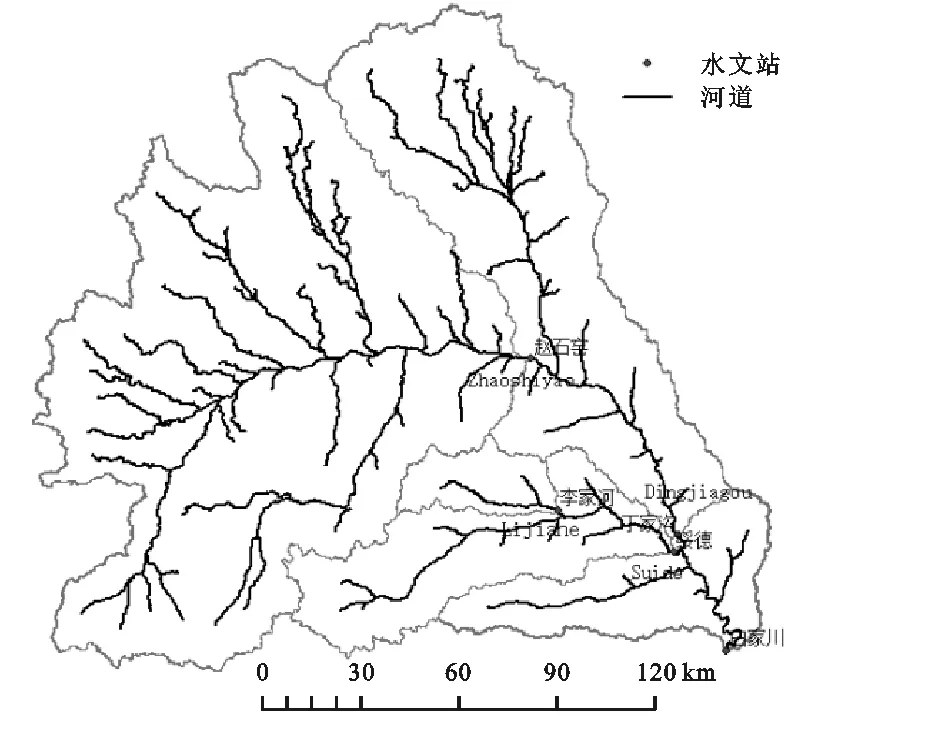
图1 无定河流域位置及水文站点分布

2.2 研究方法

目前，在研究径流侵蚀方面主要有剪切力模型和侵蚀能量模型两大类[11-14]，本文采用侵蚀能量模型中的径流侵蚀功率理论。

通过以下公式计算出径流侵蚀产沙的侵蚀动力指标：

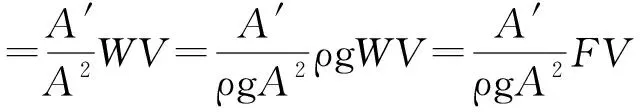
(1)

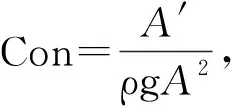
E=Con·F·V

(2)

式中：W为径流总量(m3)；A为流域面积(m2)；Qm为洪峰流量(m3/s)；A′为与Qm对应的流域出口断面的过水面积(m2)；V为流域出口断面与Qm对应的平均流速(m/s)；ρ为水的密度(kg/m3)；g为重力加速度(m/s2)；F为作用力(N)。

可以看出，指标E具有功率的量纲。本文将径流年内分配试作一次径流过程[15]，通过使用径流侵蚀功率的计算公式，计算出年径流侵蚀功率，从年尺度上研究流域径流侵蚀功率的时空变化特征。

则以下式中：各项含义分别为：

Ea=Q′m·H

(3)

本文采用Mann-Kendall非参数秩次相关检验法[16]来进行水沙变化趋势分析。可构造统计量:

(4)

式中：

(5)

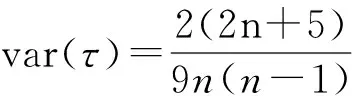
(6)

统计量U称为Kendall秩次相关系数，当n增加时，U将很快收敛于标准正态分布。给定显著性水平α，其双尾检验临界值为Uα/2，当|U|Uα/2时，系列趋势显著，如U>0,系列呈上升趋势，如U<0,系列呈下降趋势。

线性回归法通过建立年径流序列yt与相应的时序t之间的线性回归方程来检验时间序列的线性变化趋势[17-18]。线性回归方程为：

yt=at+b

(7)

式中：yt为实测序列；t为时序(t=1,2，…，n；n为序列长度)；a为斜率，表征时间序列的平均趋势变化率；b为截距。

Mann-Kendall突变点诊断法被用于进行突变年份的检验。当Mann-Kendall法用于检验序列突变性时[19]，需构造一个秩序列d：

(8)

式中：

(9)

在时间序列随机独立的假定下，dk的均值和方差可由下边两个式子计算：

(10)

(11)

定义统计变量

(12)

按时间序列逆序，再重复上述过程，同时使UBL=-UFK(L=n+1-k)，由UFK绘制出曲线C1，由UBL绘制出曲线C2。若UFK或UBL的值超过临界直线，表明序列上升或者下降趋势显著。如果C1或C2出现交点，且交点在临界线之内，那么交点对应的时刻便是突变开始的时间。

3 结果与分析

3.1 流域水沙趋势分析

通过运用M-K非参数秩次相关检验，计算5个代表水文站径流变化趋势特征，见表1。可以看出，无定河流域空间内各小流域径流量均发生了显著变化。径流量秩检验系数都为负数，径流量呈下降趋势，且绝对值随流域面积逐渐增大：白家川>丁家沟>赵石窑>绥德>李家河，无定河干流水文站显著水平0.001，支流水文站显著水平0.05，干流下降趋势比支流更显著。

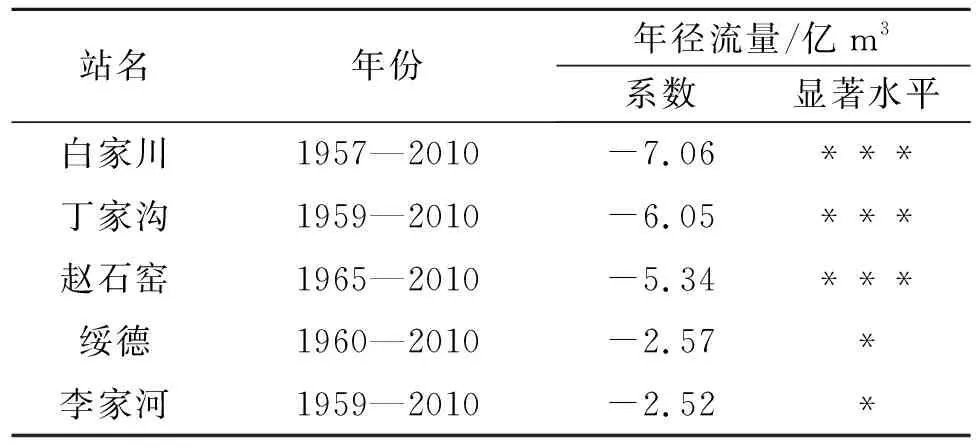
表1 年径流量变化趋势M-K非参数秩次相关检验

使用M-K检验法对无定河流域白家川站、丁家沟站、赵石窑站、绥德站、李家河站等5个水文站的年径流系列进行突变点检验，检验结果见图2。5个水文站的径流变化呈减小趋势，趋势明显超过α=0.05。由图中选取第一个交点作为突变点进行分析，可以看出，白家川站年径流系列突变点在1985年左右，丁家沟站年径流系列突变点在1979年左右，赵石窑站年径流系列突变点在1978年左右、绥德站年径流系列突变点在1974年左右，李家河站年径流系列突变点在1971年左右；说明大理河流域最早受人类活动影响，大理河一级支流小理河流域受人类活动影响更早。

图2 年径流量M-K统计量时程变化

通过统计无定河流域5个代表水文站的水沙特征，同时统计出5个水文站的年径流量在各自突变年份前后的统计特征值，见表2和表3：通过表2中可以看出，无定河流域内控制面积逐渐增大的5个水文站李家河站、绥德站、赵石窑站、丁家沟站、白家川站的年径流量、年输沙量的平均值、变异系数等统计特征都随着水文站控制的流域面积增大而有减少，说明流域面积越小径流与输沙年系列变化越不稳定，流域面积越大径流与输沙的年系列变化幅度越小，变化越稳定。研究表明，在小尺度上人类活动的影响可能更加明显、强烈。

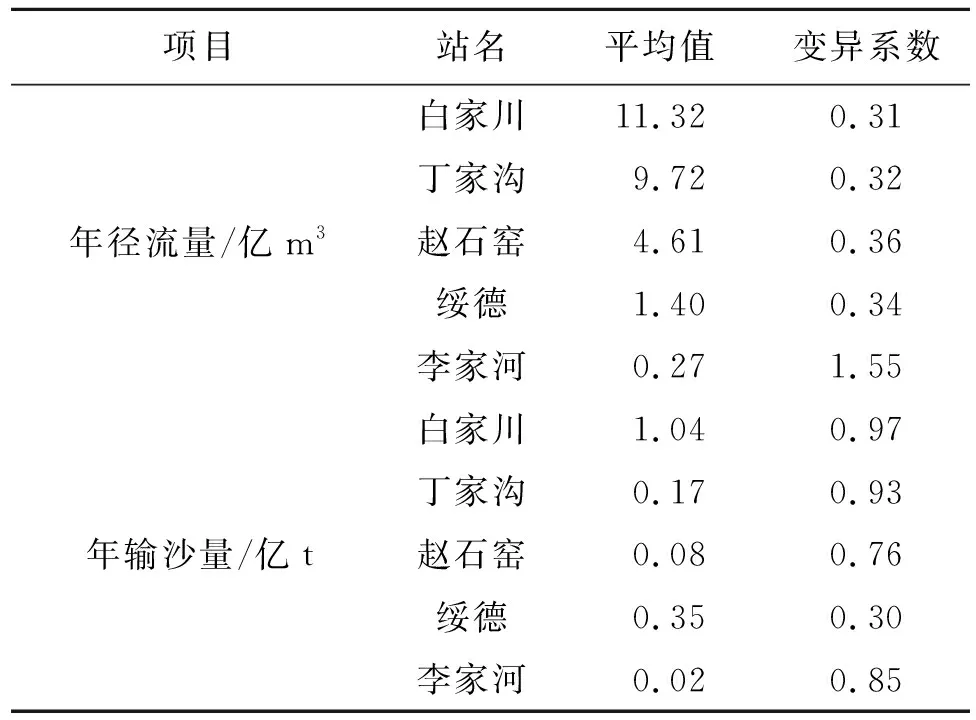
表2 无定河流域各水文站水沙特征

表3 突变前后径流量和径流侵蚀功率

由表3可以分析出，突变年份后无定河流域白家川站、丁家沟站、赵石窑站、绥德站、李家河站等5个水文站径流量的平均值、变异系数等统计特征值基本小于突变年份之前，说明突变年份后的径流系列更为稳定，同时与表2对比，发现突变年份之前的水文要素统计特征指标值比总体统计特征指标值大，突变年份之后的水文要素统计特征指标值比总体统计特征指标值小。

图3 1959-2010年长时间序列年径流侵蚀功率

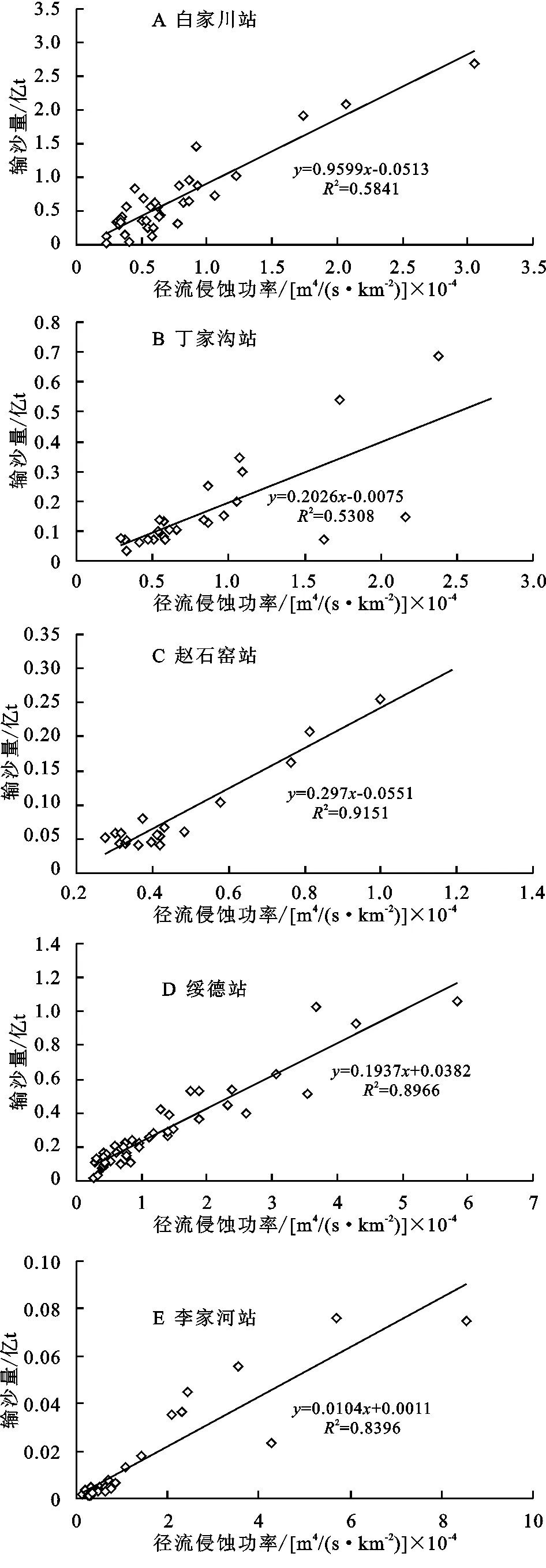
图4 径流侵蚀功率—输沙关系

3.2 流域径流侵蚀功率的时空变化特征分析

通过使用径流侵蚀功率理论，计算出了无定河流域5个水文站1956—2010年的年径流侵蚀功率，见图3。由图3可以看出，5个站点的径流侵蚀功率时间序列都呈下降减小趋势；通过统计发现白家川站、丁家沟站、赵石窑站、绥德站、李家河站的5个水文站控制流域的径流侵蚀功率的标准差等统计值，在各自径流量突变年份之前都大于突变年份后,突变年份之前流域年径流侵蚀功率平均标准差高于突变年份后，这说明突变后的侵蚀功率更为稳定。

通过对白家川站、丁家沟站、赵石窑站、绥德站和李家河站5个水文站1959—2010年长时间序列径流侵蚀功率取平均值，以及在各自突变年份之前取平均值和突变年份之后取平均值，可以分析出，无定河流域白家川站、丁家沟站、赵石窑站、绥德站和李家河站的平均径流侵蚀功率分别为0.73，1.03，0.68，2.50，18.73。随着控制流域尺度的增加呈递减小趋势，无定河支流大理河流域绥德站和小理河流域李家河站的平均径流侵蚀功率大于干流；流域平均径流侵蚀功率随着控制流域尺度的增加呈递减小趋势。突变年份之后年平均径流侵蚀功率比突变年份前平均减少1.05×10-4m4/(s·km2)，且支流径流侵蚀功率大于干流，干流侵蚀功率变化基本趋于稳定，突变年份前无定河流域白家川站、丁家沟站、赵石窑站、绥德站和李家河站的年平均径流侵蚀功率随着流域尺度增大而逐渐减小的变化规律比较明显，突变年份后无定河流域白家川站、丁家沟站、赵石窑站、绥德站和李家河站的年平均径流侵蚀功率均有所减少，随着流域尺度增大变化规律比较不明显。

3.3 径流侵蚀功率—输沙相关模型分析

通过对无定河流域5个代表水文站的年输沙量与年径流侵蚀功率线性拟合，结果见图4。根据曲线分析，无定河流域白家川站、丁家沟站、赵石窑站、绥德站、李家河站径流侵蚀功率与输沙量相关关系如图4，可以看出，径流侵蚀功率与输沙量呈线性关系，输沙量随着径流侵蚀功率的增大而增大，5个代表水文站大部分径流侵蚀功率与输沙量的关系点均密集分布在相关线左右，可以看出径流侵蚀功率与输沙量关系没有出现系统性的偏离，线性相关方程R2分别为0.85，0.53，0.92，0.90，0.89，说明了径流侵蚀功率理论在流域年尺度上能更好的表征径流侵蚀输沙关系。

4 讨 论

径流侵蚀功率理论最早是由鲁克新等人针对岔巴沟流域次暴雨洪水尺度上提出的，该理论外推到其他时空尺度需要进一步研究。研究和表征径流侵蚀输沙的理论有多种，如剪切力模型和侵蚀能量模型。本文在流域年尺度上使用了径流侵蚀功率理论，建立了无定河流域不同空间尺度的年径流侵蚀功率—输沙相关模型，可以较好的表征了径流侵蚀输沙关系，但是由于国内外在降雨侵蚀力理论上有非常丰富的研究成果[20-29]，不同时空尺度皆取得了一系列重要成果，但径流侵蚀功率和降雨侵蚀力两者的相关研究较为薄弱，需要进一步对其进行深入研究。

通过突变点检验，可以发现白家川站年径流系列有一个突变年份在1985年左右，所以将白家川站的年径流系列分为1957—1985年，1986—2010年两个时段进行对比分析，分析气候变化与人类活动对无定河流域径流变化的影响大小。

通过表4可以看出，无定河流域实测径流量在1986—2010年的年均值比基准年减少4.85亿m3,其中降水减少影响占-66.96%，人类活动影响减少占166.96%；分析减少的原因可以看出，在1986—2010年降雨量实际上是在增加的，水土保持等人类活动对径流的减少具有重要的影响，从而可以看出人类活动的影响占主导地位。同时，无定河流域实测输沙量在1981—2010年的年均值比基准年减少1.03亿t,其中降水减少影响占2.68%，人类活动影响减少占97.32%；分析减少的原因可以看出，在1981—2010年降雨量和水土保持等人类活动对输沙的减少均具有重要的影响，但人类活动的影响占主导地位。研究表明，水土保持等人类活动可能是造成无定河流域径流侵蚀功率变化的主导因素。

表4 白家川站控制流域径流输沙变化

5 结 论

(1) 无定河流域1956—2010年年径流量有显著减小趋势；径流与输沙均随流域面积的增大流域逐渐增大；径流突变年份在1971—1985年，突变年份后径流离散程度变小。

(2) 无定河流域1956—2010年年5个代表水文站年径流侵蚀功率呈下降减小趋势，线性回归系数均为负数，突变年份之前径流侵蚀功率平均标准差高于突变年份后；年平均径流侵蚀功率随流域面积的增大而减小；突变年份之后年径流侵蚀功率平均减少1.05×10-4m4/(s·km2)，且突变年份之前径流侵蚀功率递减趋势与总体保持一致。

(3) 无定河流域5个代表水文站径流侵蚀功率—输沙相关模型相关关系均显著(p<0.01)，线性相关方程R2分别为0.85，0.53，0.92，0.90，0.89，径流侵蚀功率理论在流域年尺度上能较好的表征径流侵蚀输沙关系。水土保持等人类活动可能是造成无定河流域径流侵蚀功率变化的主导因素。