基于趋势性度量的有序聚类方法探讨
2020-04-27何韩吉邓光明
何韩吉,邓光明,b
(桂林理工大学 a.理学院;b.应用统计研究所,广西 桂林 541004)
一、引 言
在常用的聚类方法中,系统聚类、K均值聚类均运用于无序样本,即样本的地位是彼此独立的。而有序聚类则是对有序样本本身进行聚类,即样本的次序是有一定关联的。因此,在实际应用中,对于样本次序不能变动的情况,催生了有序样本的聚类问题。有序聚类是研究对有序样本进行分类的一种统计方法,在多学科、多领域有着广泛的应用[1]。有序聚类算法能够比较成功地对有序样本进行一定的聚类,但是由于数据受时间的影响较大,需要对时序数据的趋势性进行考虑,提取趋势性特征对有序样本进行划分。然而,针对有序聚类的研究较少,基于趋势性特征的有序聚类研究更少。
国内外学者基于有序聚类分析方法在多方面进行了相关应用和理论探索。目前来看,对于有序聚类的研究主要包含以下两个方面。一是对有序聚类方法在其他领域的一些应用,包括在其他领域的有序聚类分析和通过有序聚类思想进行一些探索性分析。如杨毅等针对有序的面板数据时间尺度的维度问题,用主成分分析处理为一维数据,并进一步通过有序聚类进行分类,结果显示出良好的应用前景[2]。符璐等建立了以F统计量为基础的有序样本分类方法,测度空气质量影响因子影响程度的变化,从而评价政府治理环境的效应[3]。陈远中等通过趋势性特征引入了突变点,将突变点应用到有序聚类中,从而能够根据突变点对有序样本进行划分,但其方法的计算复杂度增加[4]。Li等在水文过程预测中,为了有效地提取相关特征,将有序聚类方法用于频谱分类,从而提高了预测的精确性[5]。Kashida等将甲基红染料共价结合到双链DNA中来进行有序聚类,发现甲基红团簇的光谱特征[6]。二是将现有的有序聚类方法推广到多维数据的情况中。如严广松等对多维数据进行压缩,变成一维数据,提出了投影寻踪方法、综合评判法和主成分分析法进行一维压缩;将系统聚类应用在有序样本聚类上,经过系统聚类的迭代计算获得最终的有序样本聚类结果[7]。任娟等提出了多指标面板数据融合聚类分析方法,具体是由因子分析提取信息,使用系统聚类法确定分类情况,通过有序聚类对样本进行动态分析和揭示类的演变进程[8-9]。
现有的有序聚类分析研究主要存在两个问题。一是对数据的特征体现不够。一般方法中所使用的类直径度量为平均法,因此会将均值差异较小的样本均为一类,从而忽略了数值变化的正负效应,即趋势性。二是基于趋势性改进的方法计算复杂度高。现有的方法中定义了突变点这个度量,计算的复杂度与平均法相比增加不少,且会在聚类过程中过度突出突变点,从而导致突变点单独成类的风险。本文通过构建基于邻近点斜率的度量方法,计算斜率间的均值,简化了计算复杂度,加强了趋势性度量的重要性,提出了更加突出趋势性的有序聚类分析方法。
二、有序聚类的原理与改进
(一)有序聚类的原理[10]
对于无序样本,其聚类的处理已经有了充分的研究和讨论。但是,对于存在一定相关性的样本,即有序样本,则需要考虑样本的次序。有序样本问题一般使用费希尔最优求解法来求得最优的聚类结果。设n维有序样本向量为X=(X(1),X(2),…,X(n))′,具体的算法与计算步骤如下:
1.定义类的直径。设某一类G包含的样本是{X(i),X(i+1),…,X(j)},该类的均值坐标为:
(1)
用D(i,j)表示这一类的直径,直径可定义为:
(2)
2.定义分类的损失函数。费希尔最优求解法定义的分类损失函数的思想类似于系统聚类法中的Ward法,即要求分类后产生的离差平方和的增量最小。用b(n,k)表示将n个有序样本分为k类的某一种分法:
G1={i1,i1+1,…,i2-1},
G2={i2,i2+1,…,i3-1},
…
Gk={ik,ik+1,…,n}
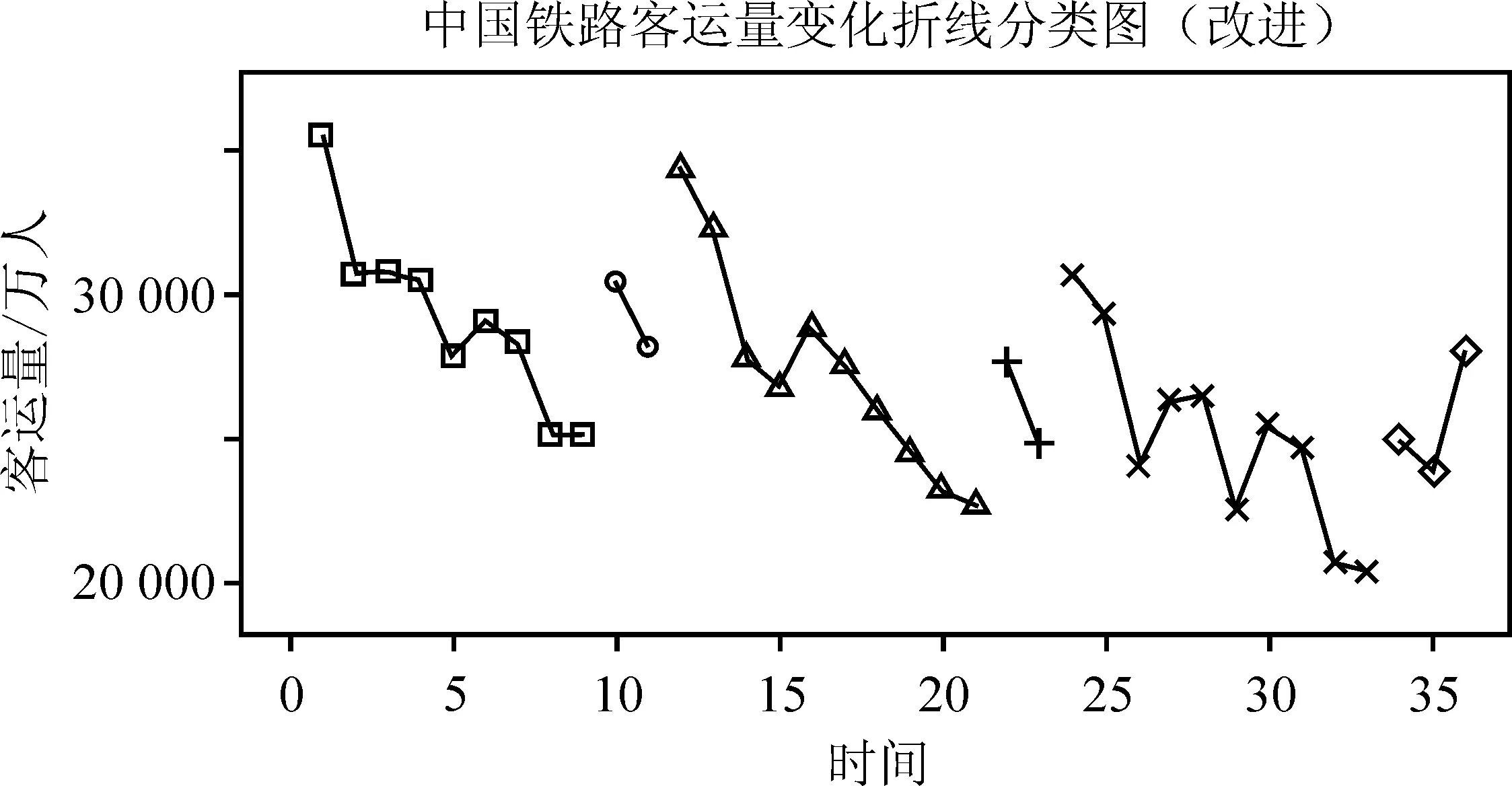
其中,i1=1 (3) 其中ik+1=n+1。 3.求最优分类法的递推公式。算法思想是寻找最优分割点jk,使分类后产生的离差平方和的增量最小,即求出使得L[b(n,k)]最小的最优分类法,记为p(n,k)。因此,我们得到费希尔最优求解法的递推公式为: (4) 针对样本均值类直径的度量,会导致在一些时序中,聚类结果偏向于极值点,从而不能很好地反映序列的趋势情况。所以,本文提出了基于序列斜率的类直径计算方法,力求表现序列的趋势,将同一趋势的样本划为同一类。具体的算法与计算步骤如下: 1.计算相邻序列之间的斜率。假设某一p维有序样本向量为Y=(Y(1),Y(2),…,Y(p))′,对应的p维时序向量为t=(t(1),t(2),…,t(p))′,则相邻序列之间的斜率为: (5) 则新的斜率序列Lij={li,i+1,li+1,i+2,…,lj-2,j-1,lj-1,j}。 2.根据斜率定义类的直径。设某一类G包含的样本是{Y(i),Y(i+1),…,Y(j)},则对应的斜率样本为{li,i+1,li+1,i+2,…,lj-2,j-1,lj-1,j},此类的均值坐标为: (6) 用D(i,j)表示这一类的直径,被定义为: (7) 不难发现,如果某一类别只包含两个样本,那么其D(i,j)≡0,说明最少三个样本或者三个时序数据,才能看出一定的发展趋势,这与我们的常识也是相符合的。此外,当斜率相等时,直径为0,说明它们之间的差异很小;当出现斜率的较大变化时,直径会变大,从而说明它们之间的差异比较大。 对比较特殊的单调性数据和比较复杂的波动性数据进行数值模拟,揭示新方法的优势。 首先,考虑在单调性数据上的模拟。需要生成具有五组不同斜率的时序数据的递增序列,实验数据具体为:第一组为1~21、等差为1的序列;第二组为23~41、等差为2的序列;第三组为44~71、等差为3的序列;第四组为72~81、等差为1的序列;第五组为83~99、等差为2的序列。一共为60个时序数据。如图1所示,整体为一递增序列,但是各段的斜率和上升速度有所差异。 图1 单调上升序列折线图 为了更好地比较两种方法,假定序列聚为5类,比较两种情况之下聚类的差异,以及与实际情况相比的正确性。如表1所示,表中的组内成员为序列号,可以发现改进后的方法与本文初始生成的五组数据完全吻合,而原始方法却在第3~5类出现了一些偏差。因此,在单调序列的应用上,改进后的方法能够提高聚类的精度和准确性,并且更能够体现时序数据的趋势性。 表1 单调序列模拟结果 进一步通过图2的图像比较可以看到,原始方法在斜率出现变化时会出现误判的情况,不能在趋势上完成正确的聚类。而改进后的方法则完全将上升速度相同的时间点聚为了一类,体现了改进方法的优越性。 图2 单调上升序列聚类结果图 其次,考虑在时序中比较常见的波动性数据,即存在一些周期性特征的时序数据,生成具有五组不同斜率的时序数据的递增序列。实验数据为:第一组为1~10、等差为1的序列;第二组为9.5~5、等差为0.5的序列;第三组为7~25、等差为2的序列;第四组为25~16、等差为1的序列;第五组为17~35、等差为2的序列;第六组为33~25、等差为1的序列。一共为60个时序数据,如图3所示。 图3 波动上升序列折线图 与单调上升序列类似,假定聚为6类,比较两种情况之下聚类的差异,以及与实际情况相比的正确性。如表2所示,可以发现改进后的方法与我们初始生成的五组数据完全吻合;而原始方法却出现了截然不同的结果,更加偏向于在波峰与波谷处进行聚类,即趋势转折点。对斜率的变化明显不够敏感。因此,在波动性序列的应用上,改进后的方法能够准确地识别出上升和下降的趋势,这对于在高频数据上的趋势性提取有着较为广泛的应用性。 表2 波动序列模拟结果 进一步通过图4的图像比较可以看到,原始方法在转折点处进行聚类,由转折点向两侧分布,不能在趋势上完成正确的聚类。而改进后的方法则可以将同样上升或下降速度的点聚为一类,更加能够体现序列的趋势变化。 图4 波动上升序列聚类结果图 本文选取了中国2016年8月至2019年7月铁路客运量月度数据,单位为万人,从而通过这些数据寻找中国铁路客运量的规律。数据来源为国家统计局网站,使用R语言进行实证分析。图5为客运量的折线图,由于波动较多,很难看出整体趋势和客运量的规律变化。 图5 铁路客运量月度数据折线图 从表3可以看出,相邻时间聚成的类直径均为0,与上面讨论的结果一致。由于数据的量级比较大,所以类的直径比较大,但是不影响聚类效果。 表3 类的直径 表4中我们得到了最小分类损失,通过它进行进一步的聚类选择。 表4 最小分类损失函数 一般通过常识来确定分类的数量,否则可以从L[p(n,k)]随k的变化趋势图中找到拐点处,根据拐点处信息确定k。从图6中看到,在k=6时,有一次拐点,所以聚类个数确定为6个。 图6 k与L[p(n,k)]的关系 基于改进的有序聚类方法,得到了有序聚类结果。由表5所示,不难发现铁路客运量的规律特征,每两类几乎是对应着相同的月份,即在一年的时间内,客运量存在着两种发展态势。这样的聚类结果是符合客观事实的,可以说改进的有序聚类方法是有效的。 表5 有序聚类结果 通过表6中的数据对比两种聚类方法,可以直观看出,两种方法对客运量都进行了较好的划分,但是我们进一步通过图7和图8对比发现,改进之后的聚类结果更能够体现趋势性特征,并且可以看出铁路客运量受到季节性因素的影响,全年有两段时期:每年的9-10月的波动下降期,11月到次年8月的持续上升期;而原始方法的聚类则看不出这样的趋势存在,只是将接近的数值聚在了同一类中,只能看出每年的铁路客运量的高峰集聚区和低谷集聚区。 表6 平均法与斜率法的结果对比 图7 铁路客运量月度数据斜率度量聚类结果折线图 图8 铁路客运量月度数据平均度量聚类结果折线图 本文针对有序聚类对波动性时序数据聚类的情况下,不能很好地对同一趋势的样本进行有效聚类的情况,考虑了时序的趋势性特征,提出了改进的类直径度量方法,使用了斜率来对直径进行度量。该方法可以很好地提取时序数据的趋势性特征,从而对相同趋势的样本进行聚类。模拟结果表明:对于同类数据的识别,改进的方法正确率更高,聚类效果更好;尤其是对波动性数据的聚类,改进的方法性能远远高于原有方法。实证分析也再次说明,基于趋势性度量改进的有序聚类方法的聚类结果贴合实际情况,并且突出了趋势性特征的表现,能够对大量时序数据进行有效的有序聚类。
(二)改进类的直径
三、数值模拟
(一)单调性数据


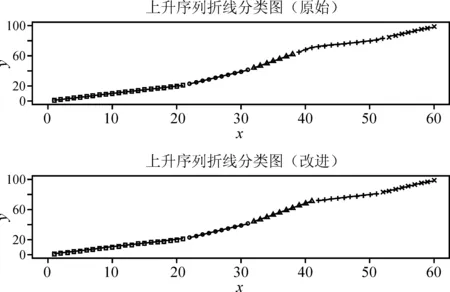
(二)波动性数据



四、实证分析
(一)数据来源
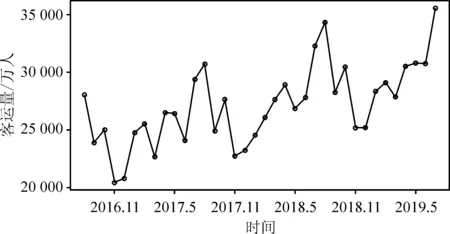
(二)定义斜率类直径

(三)计算最小分类损失函数

(四)聚类数量的确定
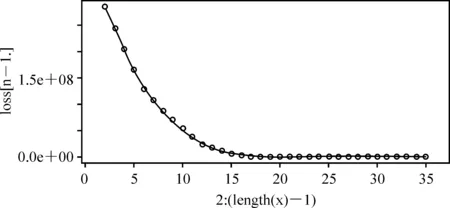
(五)基于斜率度量的有序聚类结果
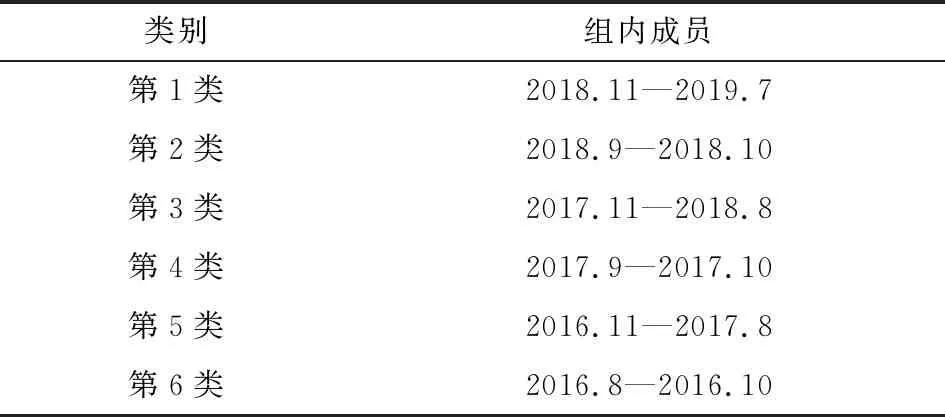
(六)与原有方法的比较


五、结 论
