船舶抛锚过程中落锚贯入深度研究
2020-04-27汪嘉钰别社安
刘 润,汪嘉钰,别社安
船舶抛锚过程中落锚贯入深度研究
刘 润,汪嘉钰,别社安
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
落锚作业是船舶抛锚定位过程的第1个环节,在落锚过程中,船锚不仅可能直接撞击海底管线造成危害,而且船锚的贯入深度会影响拖锚的运动轨迹,从而间接影响海底结构物的运行安全,可见确定船舶落锚阶段船锚的最终贯入深度十分重要.为此,首先开展一系列小比尺落锚模型试验,分别研究在黏性土和无黏性土中船锚质量和落锚高度对霍尔锚和大抓力锚最终贯入深度的影响,发现贯入深度随船锚质量和落锚高度的增加而呈非线性增加,但增幅不断减缓.然后,结合小比尺模型试验,采用能量法和太沙基极限承载力公式拟合船锚贯入深度的计算公式,并确定式中的经验系数.另外,在小比尺模型试验的基础上,验证船舶落锚的数值模拟方法,并对原型船锚的贯入过程进行分析,讨论贯入过程中船锚姿态变化的过程和规律,以进一步揭示落锚贯入深度与船锚触底动能之间的关系.最后,开展现场船舶落锚试验,对比分析本文公式、Young公式、DNV坠物公式、DNV落管公式与现场实测数据之间的差异,发现试验结果和本文公式吻合良好,在验证本文公式正确性的同时阐明了其他理论算法的适用条件与局限性.
海底管线;落锚;贯入深度;现场试验
随着我国海洋航运事业的不断发展,船舶锚害已经成为影响海底管线安全运行的重要因素,其中落锚作业作为船舶抛锚过程中的第1个环节,不但可能直接撞击海底管线,对海底管线造成无法修复的破坏,同时落锚贯入深度对拖锚的运动轨迹影响显著,因此研究落锚贯入深度对于保护海底管线有重要意义.
为研究落锚贯入深度,国内外许多学者基于运动法则和能量法对船舶落锚过程进行了大量研究. Wierzbicki等[1]给出了海底管线凹痕深度和坠落物体动能之间的关系.张磊[2]和李庆等[3]结合DNV规范[4]及牛顿第二定律研究了落锚贯入深度,并建立了理论计算方法.雷震名等[5]基于DNV规范中的能量法和试验展开了落锚过程对海底管线影响的研究.李学东等[6]在国内首次利用Young公式建立船锚贯入深度的计算模型,并对公式中各项系数进行了详细讨论,还根据日本的投锚试验结果确定了公式中船锚的形状系数.近年来,数值计算工具被广泛应用于船舶落锚的研究.王懿等[7]利用CEL数值模拟方法对船舶落锚贯入深度与落锚速度、海洋土体的强度参数之间的关系进行了研究,发现随着落锚速度的增加和土体强度的降低,船锚贯入深度逐渐增大.对处于碎石保护下的管线,肖鹏[8]和邱长林等[9]分别利用离散元和FEM-DEM耦合的计算方法对管线堆石保护层在船锚碰撞作用下的破坏变形进行数值分析,认为保护层在落锚过程中可以提供竖直向抗力以降低船锚对海底电缆的影响,并建立了冲击荷载作用下在碎石保护层中的海底管线受力与变形分析方法.韩聪聪 等[10]和陈峰等[11]利用室内小比尺模型试验方法分别讨论了不同船锚的落锚贯入深度,并提出了相应的经验公式.综上所述,分析船舶落锚的入土体过程时,现有计算方法主要以DNV规范中落管或坠物刺入碎石保护层的公式为基础,或者利用经验公式对某种特定类型的船锚进行拟合,公式的合理性及适用性均有待进一步试验研究.
在借鉴国内外研究经验的基础上,本文综合采用模型试验、数值分析和现场试验相结合的方法对船舶落锚的贯入深度进行研究.
1 落锚贯入深度的模型试验及理论分析
1.1 试验方案
为研究不同质量的船锚在落锚过程中的贯入深度,分别设计了无黏性土与黏性土两种土质的落锚试验.在试验过程中,由起吊设备将模型试验锚提升至泥面以上的预定高度,让模型锚自由下落,直至贯入土体后停止运动,测量船锚在土中的贯入深度.试验装置如图1所示.
模型试验中分别按1∶6的几何比尺制作霍尔锚和大抓力锚两种形式的模型锚,霍尔锚共设计制作4种尺寸,船锚质量从大到小依次为76.20kg、31.25kg、15.40kg和6.45kg;大抓力锚共设计制作3种尺寸,船锚质量从大到小依次为73.00kg、25.30kg和4.70kg.模型锚如图2所示.

图2 不同比尺的模型试验锚
落锚模型试验分别在天津大学土工模型实验室的中砂土池和粉质黏土池中进行,土池均为4m×4m的正方形模型槽,土体厚度为2m.因为在实际工程中,船舶落锚时通常会利用锚机控制落锚速度,船锚下落过程不是理想落体运动,水对船锚的影响不是船锚最终落锚速度的主要控制因素,因此本文仅在理想状况下讨论触底动能不同时的落锚贯入深度,不考虑水对落锚速度的影响,即土体上方没有水.
取原状土体进行室内试验,得到中砂的天然容重为20.5kN/m3,内摩擦角为33.3°;粉质黏土的容重为21.0kN/m3,内摩擦角为31.8°,凝聚力为30.4kPa.
对每种模型锚分别进行6种不同高度的落锚试验,落锚高度分别为0.2m、0.4m、0.6m、0.8m、1.0m和1.2m,记录试验结束后船锚贯入的深度.共进行84组试验,具体试验方案如表1和表2所示.
表1 霍尔锚落锚试验方案

Tab.1 Drop test plans for the hall anchor
1.2 试验结果
分别将无黏性土中不同质量霍尔锚和大抓力锚的试验数据进行整理,如图3所示,其中为落锚高度,为贯入深度.
观察无黏性土中落锚试验数据可以发现,船锚贯入深度随着落锚高度和船锚质量的增加而增加.图4为黏性土中不同质量霍尔锚和大抓力锚的试验数据. 黏性土中落锚贯入深度变化规律与无黏性土中基本相同,船锚贯入深度也随着落锚高度和船锚质量的增加而增加.
表2 大抓力锚落锚试验方案
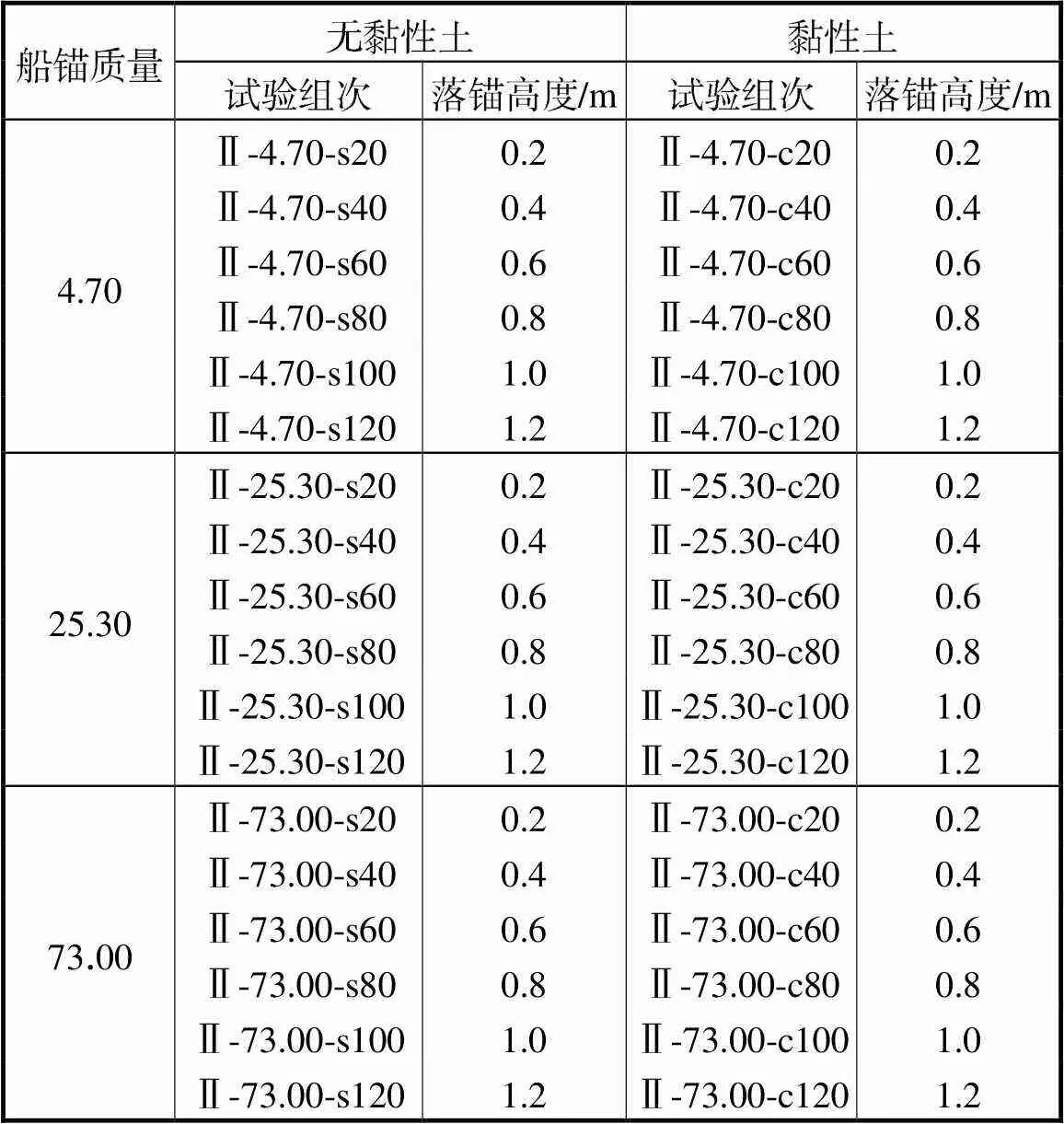
Tab.2 Drop test plans for the high holding power anchor

图3 无黏性土中落锚贯入深度试验数据
根据上述试验数据可以推测,船锚的贯入深度与落锚过程中船锚的触底动能有关,忽略船锚在自由落体过程中的能量损耗,将无黏性土试验和黏性土试验中船锚触底动能与船锚贯入深度的关系绘制于图5,其中v为触底动能.
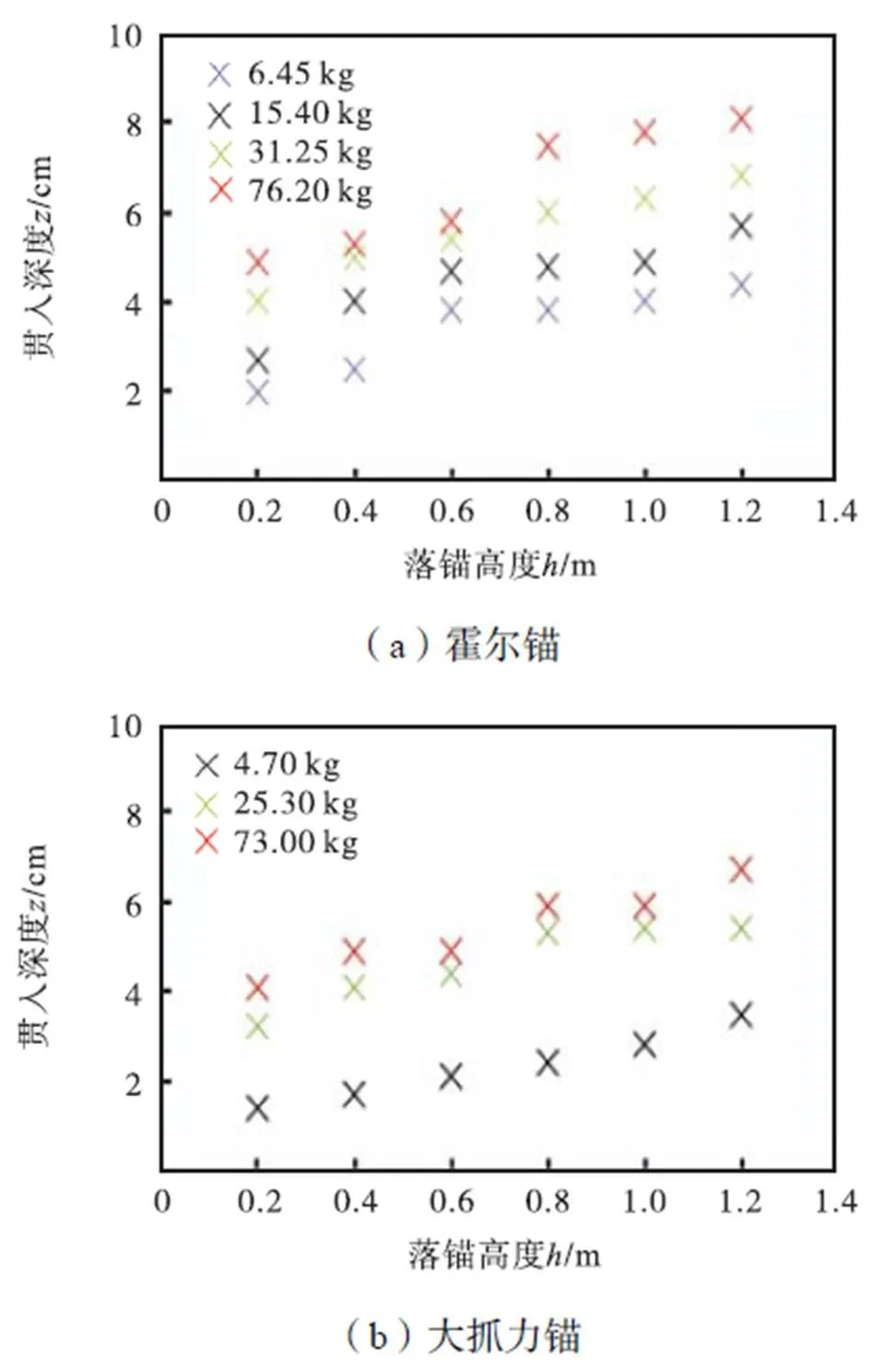
图4 黏性土中落锚贯入深度
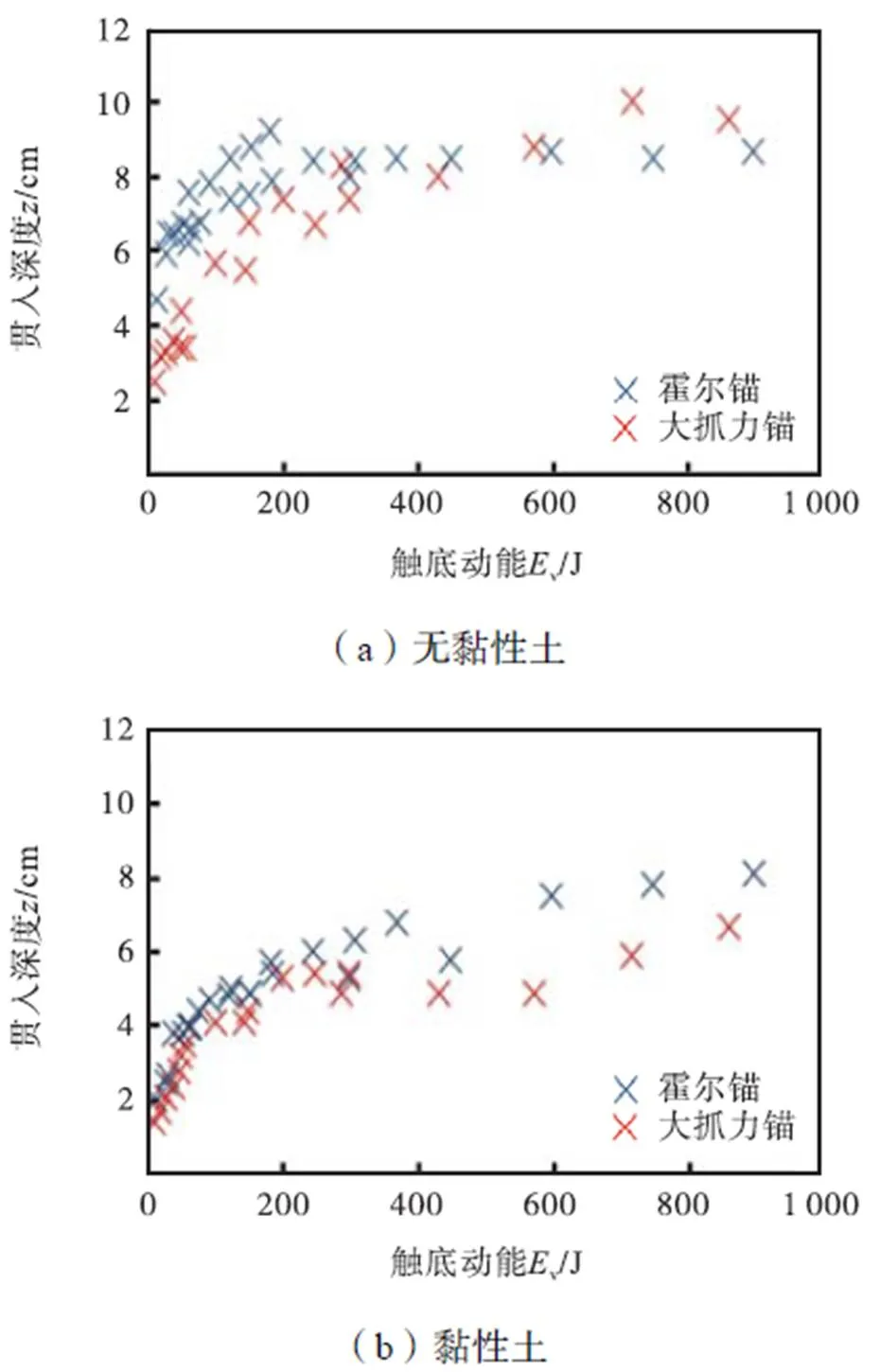
图5 落锚贯入深度与触底动能之间关系的模型试验结果
由图5可知,在黏性土和无黏性土中船锚贯入深度随触底动能的变化规律基本相同,即贯入深度随着触底动能的增大而增加,但是两者之间为非线性关系.在船锚触底动能较小时,贯入深度的增幅很大;随着船锚触底动能的增大,曲线趋于水平.在无黏性土中,霍尔锚和大抓力锚的贯入深度变化规律基本保持一致;在黏性土中,两种船锚的贯入深度在船锚触底动能较小时基本没有差别,随着船锚触底动能的增大,霍尔锚的贯入深度明显大于大抓力锚的贯入深度,在船锚触底动能达到850J时,大抓力锚较霍尔锚的贯入深度降低了16.92%.分析原因认为,两种船锚之间的差别主要来自于锚冠形状,而锚冠形状直接影响船锚与土体接触面积的大小,因此在计算实际工程中船锚贯入深度时应充分考虑船锚形状对贯入深度的影响.
1.3 船舶落锚贯入深度的确定
从试验结果可以看出船锚贯入深度与触底动能之间有一定关系,因此采用能量法计算船锚贯入深度,假定船锚的触底动能被土体完全吸收,土体对船锚的作用力采用太沙基极限承载力公式进行计算,具体为
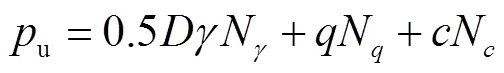
式中:N、N和N为承载力系数;为基础宽度,m;为土体容重,N/m3;为土体边载,N/m2;为土体黏聚力,N/m2.
船舶落锚过程中,一般不会修正船锚姿态,因此船锚与土体接触时,可以认为锚冠斜刺入土体.考虑到锚冠形状,基础宽度随着船锚贯入深度的增加而增加,认为二者之间具有线性关系,即=,为形状系数.基础长度同样随着贯入深度的增加而增加,即=.边载也与船锚贯入深度有线性关系,=.根据上述假定,可以得到土体对船锚的作用力为

式中anchor为土体对船锚的作用力,N.在贯入土体过程中,船锚达到贯入深度时土体对船锚所做的功为
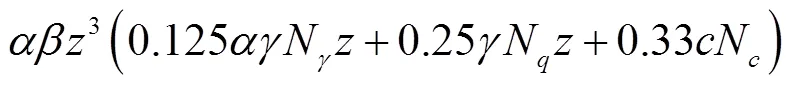
根据能量守恒原理,土体对船锚所做的功等于船锚的触底动能,即=v,考虑到船锚在贯入土体的过程中会存在能量损耗,引入经验系数,则船锚触底动能v的表达式为
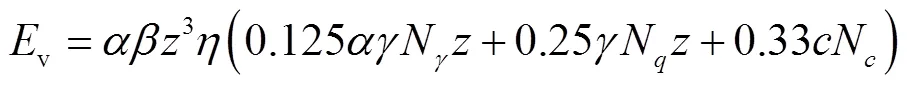
将式(4)进行化简,分别用经验系数、、代替式(4)中的参数表达式,即=0.1252,=0.25,=0.33,可以得到简化公式为
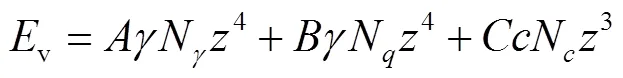
利用式(5)对无黏性土的试验数据进行拟合,试验用无黏性土的内摩擦角=33.3°,黏聚力=0kPa,可以得到N=52.8,N=36.6,N=36.0.因为=0kPa,式(5)可简化为

将所有试验数据代入式(6),通过最小二乘法可以得到=9.10,=0.75,则无黏性土中船锚触底动能v的计算公式为
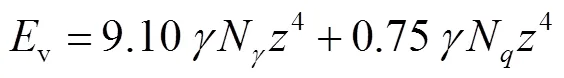
试验中黏性土的内摩擦角=31.8°,黏聚力=30.4kPa,可以得到N=44.4,N=28.7,=28.由无黏性土试验可以得到=9.10,=0.75,代入式(5),有
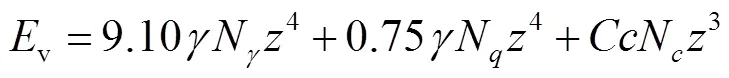
由经验系数和的表达式可以得到/=1.32,通过无黏性土试验已经得到=0.75,所以=1.00,则黏性土中船锚触底动能v的计算公式为
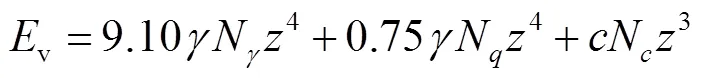
将无黏性土和黏性土的计算值与试验数据分别进行比较可以得到图6所示结果.
由图6可知,霍尔锚的贯入深度试验值普遍略大于公式的计算结果,而大抓力锚的贯入深度试验值则普遍略小于公式的计算结果,原因为两种船锚的底部结构存在一定差异,霍尔锚底部为多面体,船锚触底时通常是多面体的顶点与土体优先接触,而大抓力锚底部仅有一个平面,船锚触底时,通常为船锚底部的一条边线与土体接触,因此试验中霍尔锚的贯入深度通常大于大抓力锚.拟合公式的计算值与试验值误差在允许范围内,因此利用式(5)进行拟合是合理的,由式(5)得到的式(7)和式(9)可以计算不同质量船锚在不同触底动能时的贯入深度.
2 落锚贯入深度的数值模拟
2.1 数值模拟方法及模型
采用ABAQUS有限元软件对落锚过程进行了数值分析,并利用室内模型试验数据验证其合理性.
采用动力显示法对落锚过程进行数值模拟,计算模型由锚和地基土组成.锚尺寸与模型锚一致,具体计算模型如图7所示.
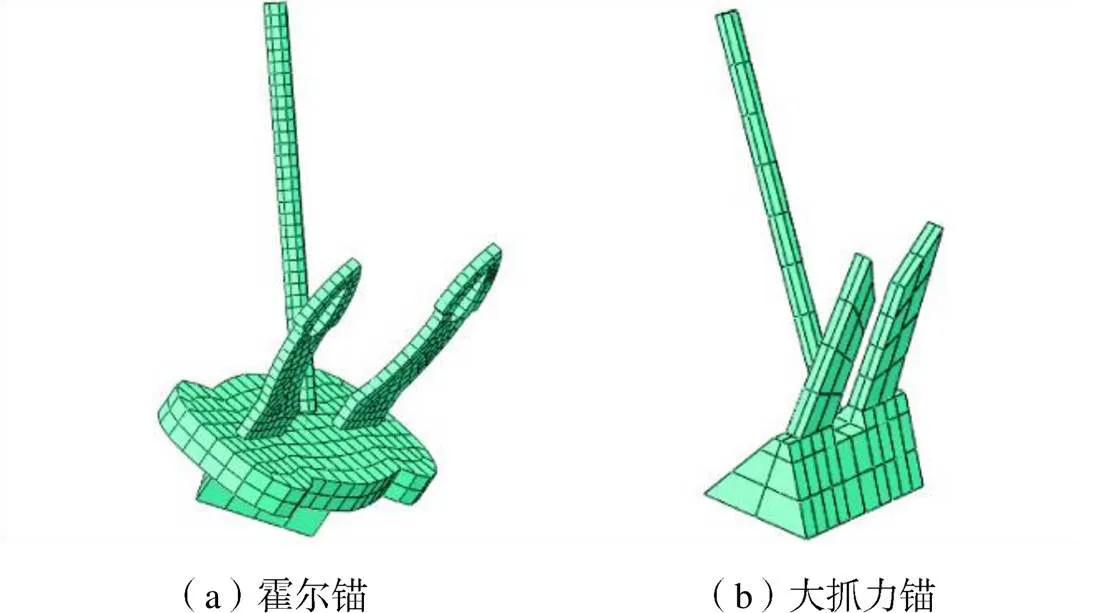
图7 模型锚网格划分
为避免边界效应,将地基土设置为直径2m、深度2m的圆形实体模型,对土体侧面、两个方向进行约束,对土体底面全部3个方向进行约束.土体的物理力学参数如表3所示,图8为其计算模型.
表3 土体物理力学参数

Tab.3 Physical and mechanical properties of soils
2.2 数值模拟结果
图9分别给出了无黏性土与黏性土中落锚贯入深度与船锚触底动能之间关系的数值模拟结果.
通过图9可以看出,随着的船锚触底动能增加,最终的贯入深度逐渐增加;霍尔锚和大抓力锚在触底动能较小时,两种船锚的贯入深度接近,随着船锚触底动能的增加,船锚的贯入深度出现不同程度的差异.无黏性土中,在触底动能达到850J时,大抓力锚较霍尔锚的贯入深度降低了9.45%;黏性土中,在触底动能达到850J时,大抓力锚较霍尔锚的贯入深度降低了23.70%,和模型试验趋势基本一致.

图8 地基土模型网格划分
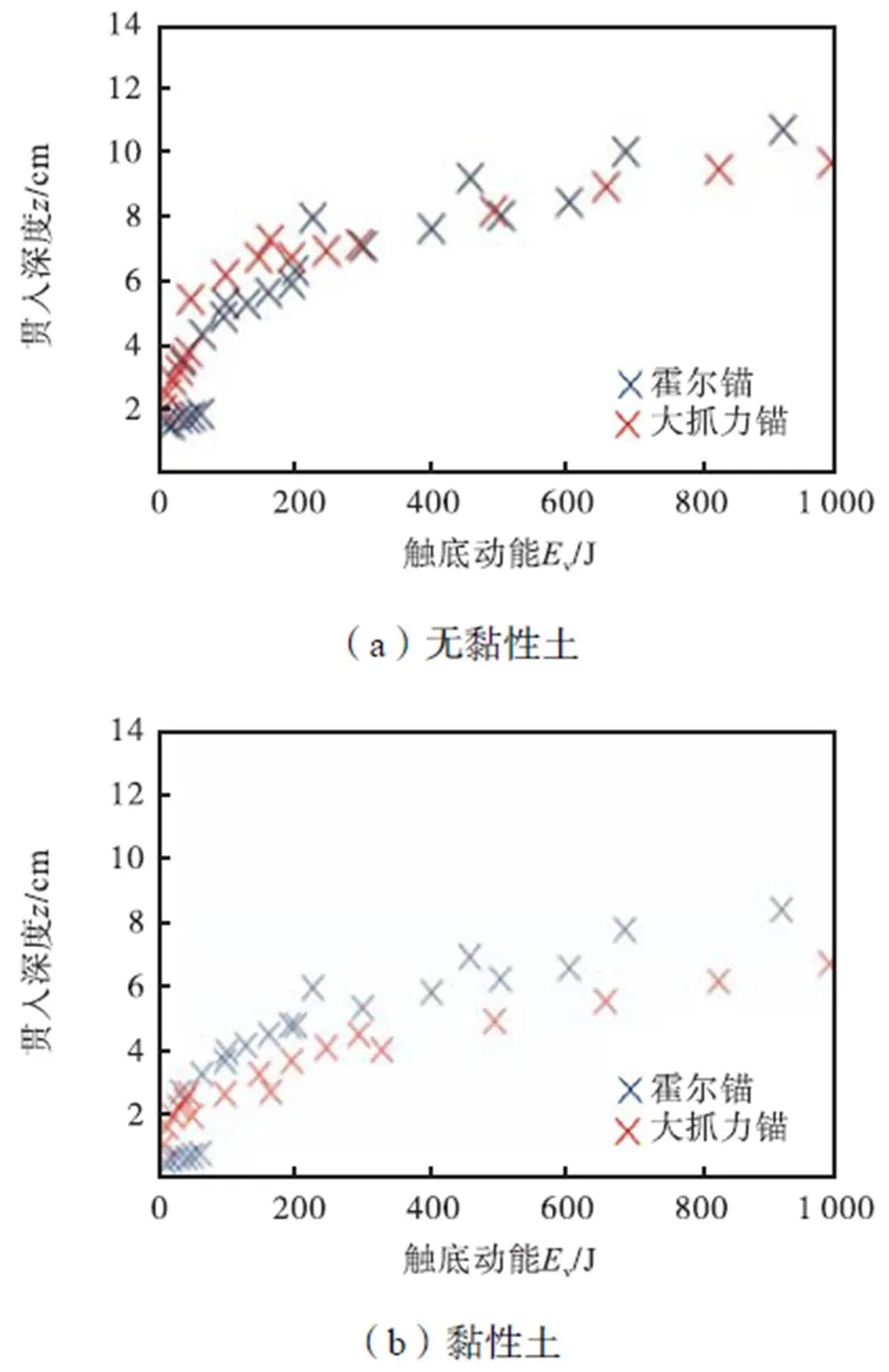
图9 落锚贯入深度与触底动能之间关系的数值模拟结果
为进一步验证数值计算的准确性,图10分别给出了两种船锚在不同土体中贯入深度的数值模拟结果与试验结果的对比.
从图10可以看出,数值模拟结果与室内模型试验结果吻合较好,证明了数值方法模拟落锚试验的可行性.
为进一步验证式(7)与式(9)对实际工程船锚的适用性,采用数值模拟方法计算了原型霍尔锚和大抓力锚在不同落速下的贯入深度.依据《GB/T 546—1997霍尔锚》[12]和《CB/T 3972—2005AC-14大抓力锚》[13]中所列举出的最大船锚尺寸进行建模,其中霍尔锚的名义质量为46000kg,数值模型中船锚的实际质量为41305.2kg;大抓力锚的名义质量为20625kg,数值模型中船锚的实际质量为13281.4kg.文献[7,14]中对船锚最终落速的计算方法做出了解释,当水深大于25m时,通常用锚机刹减锚链速度,控制最大落锚速度在2.5m/s以内,此时以2.5m/s作为船锚的最终落速;当水深小于25m时,不用锚机刹车刹减出链速度.因此,对两种船锚分别以2.5m/s、5.0m/s、7.5m/s和10.0m/s的速度进行贯入深度的研究.由于大抓力锚的质量相对较小,对其补充计算了12m/s、15m/s和17m/s时的贯入深度.图11为落锚过程中土体的等效塑性应变云图.
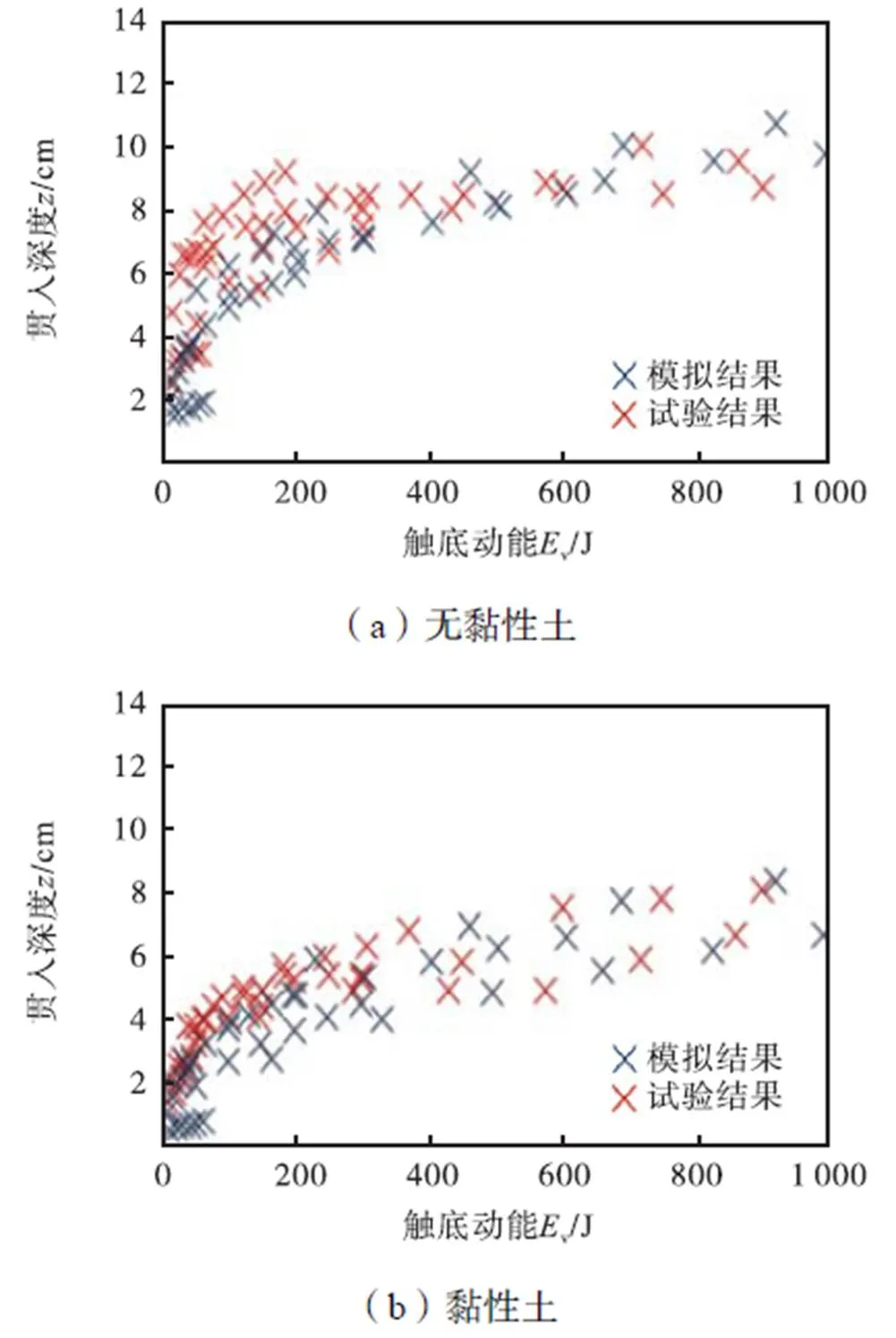
图10 数值模拟结果与模型试验结果对比
按船锚姿态可将落锚过程分为入土阶段、调整阶段和稳定阶段.入土阶段如图11(a)和图11(d)所示,此时船锚与土体刚刚接触,船锚速度最大,动能最大;图11(b)和图11(e)为调整阶段,此时船锚能量被土体逐渐吸收,船锚速度逐渐减缓,由于土体对锚的反力作用,锚杆与锚冠之间的铰接角度变小;图11(c)和图11(f)为稳定阶段,此时土体对船锚的反力作用逐渐减弱,能量逐渐耗散,锚杆与锚冠之间的铰接角度在重力作用下逐渐变大,地基土逐渐隆起.
对原型船锚进行数值模拟,并与式(7)、式(9)的计算结果进行比较,如图12所示.
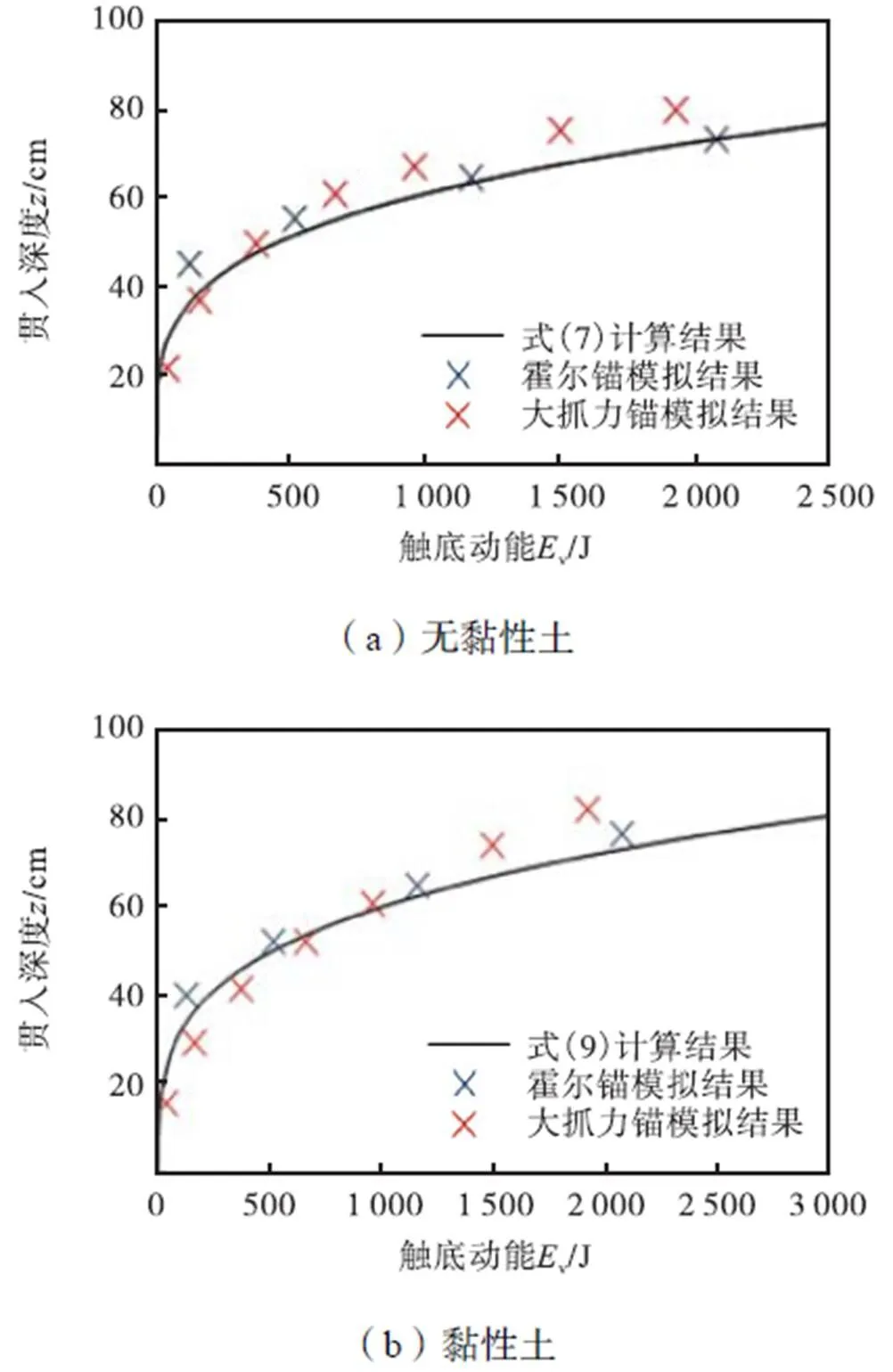
图12 式(7)、式(9)计算结果与数值模拟结果对比
由图12可以看出,在船锚具有较大触底动能时,利用式(7)和(9)仍然能够准确计算出霍尔锚及大抓力锚在不同土体性质条件下的贯入深度,说明了公式的可靠性.
3 对比与验证
3.1 现场试验
为验证船锚贯入深度理论计算的准确性,在山东滨州港地区对0.7t和1.5t两种质量的船锚进行了现场试验,如图13所示.

图13 船锚现场试验
根据勘察报告可以得到试验现场土层的物理力学性质,其中土体的天然容重为16.8kN/m3,含水率为51.7%,内摩擦角为9.7°,凝聚力为15.8kPa.试验现场土层为淤泥质黏土,因此采用式(9)计算船锚的贯入深度.现场试验中水深、理论计算结果与实测值如表4所示.
表4 落锚贯入深度现场实测值与式(9)计算值的对比

Tab.4 Comparison of the results of the field test and cal-culation from Eq.(9)
由表4可以看出,由式(9)计算出的落锚贯入深度和现场实测值有一定差异.分析认为,室内试验与现场试验所用船锚的外形存在较大差异,导致计算结果出现偏差.
3.2 现有落锚贯入深度计算方法的对比
DNV规范[4]中针对海洋的落管和坠物提出了相应的贯入深度公式,分别为

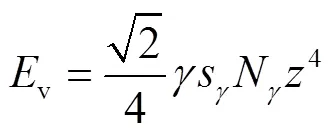
式中:为船锚的等效直径;p为船锚的投影面积;s为形状系数,DNV规范中建议取值0.6.
Young公式[6]同样为计算物体贯入深度的经典公式.将船锚接触土体时的速度作为依据,以61m/s作为分界点,Young公式分为两个经验公式.因为在落锚过程中船锚的速度很难达到61m/s,所以只需考虑速度小于61m/s的情况,此时贯入深度计算公式为
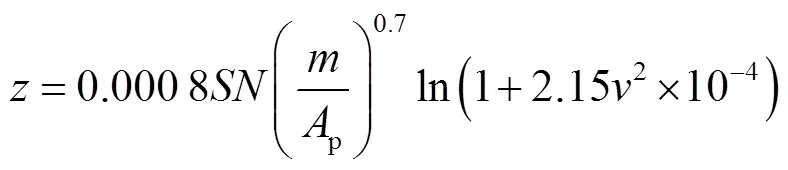
式中:为物体的形状系数;为土体系数;为船锚质量;为船锚接触土体时的速度.
对于试验用锚,根据现场试验土层资料,用式(9)~(12)分别计算落锚贯入深度,图14为不同公式计算结果和实测值的对比.
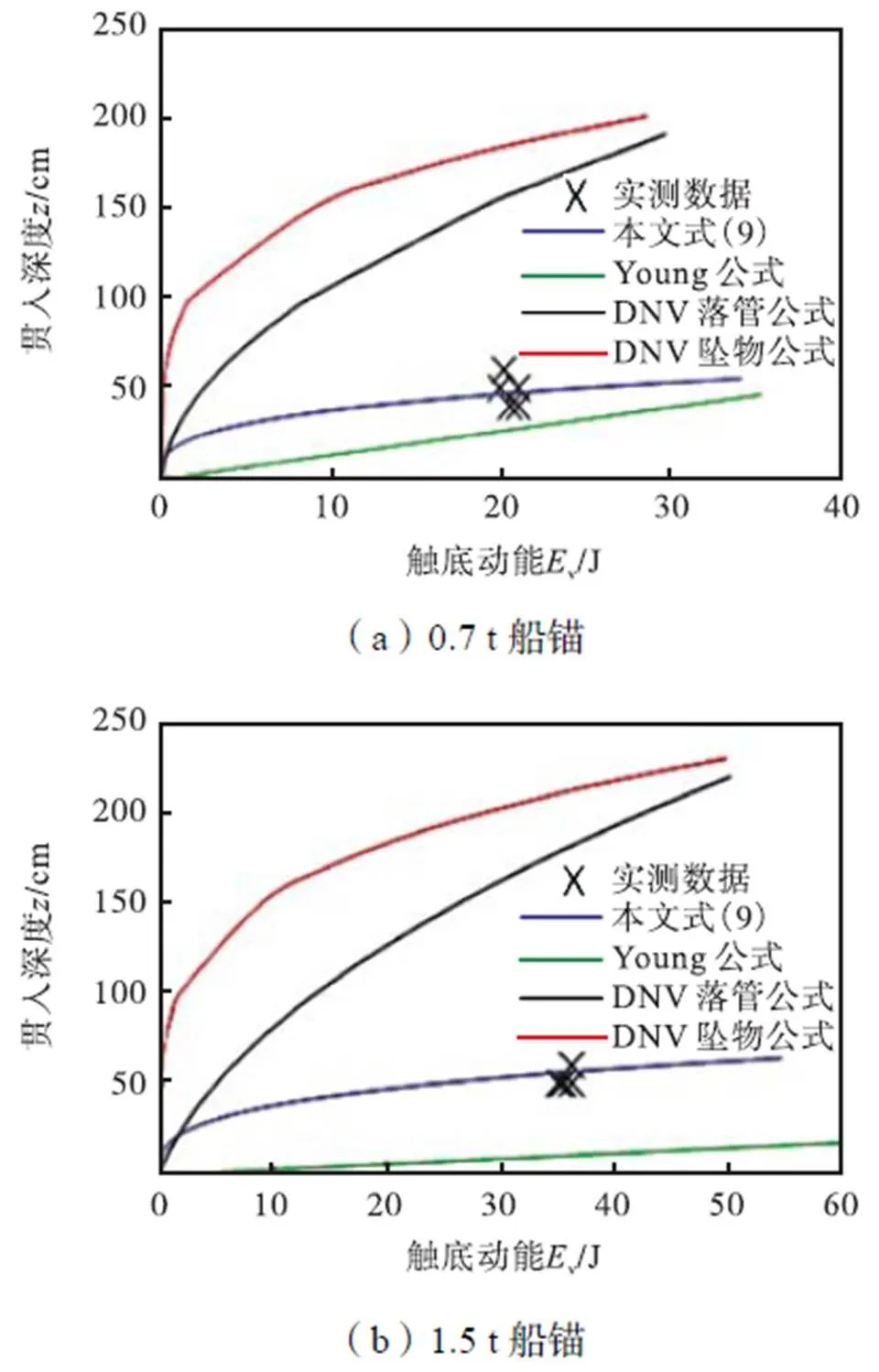
图14 不同公式计算结果与现场试验结果对比
从图14可以看出,DNV规范公式及Young公式的计算结果与现场试验测试结果有明显差异.为研究DNV规范公式与实测值之间差异产生的原因,分析了现场试验用1.5t船锚以35kJ的触底动能接触土体时最终贯入深度与土体内摩擦角之间的关系,如图15所示.因Young公式中没有与内摩擦角相关的参数,所以无法得出两者之间的具体关系.
从图15可以看出,随着土体内摩擦角的减小,DNV规范公式的计算结果迅速增大.坠物公式(即式(11))的计算结果始终大于式(9)的计算结果,而落管公式(即式(10))则在内摩擦角大于20°时,与式(9)的计算结果相近.究其原因,现阶段常用的DNV规范公式没有考虑土体黏聚力对落锚贯入深度的影响,仅适用于落管或集装箱等形状坠物贯入碎石保护层深度的计算.Young公式虽然是根据落锚试验结果拟合得到的,但该公式中与土体性质相关的参数为经验值,不能反映船锚贯入深度与土体强度的关系,因此造成该公式的局限性.本文提出的计算公式同时考虑了船锚的形状和土体强度对落锚贯入深度的影响,提高了该公式的适用性和准确性.
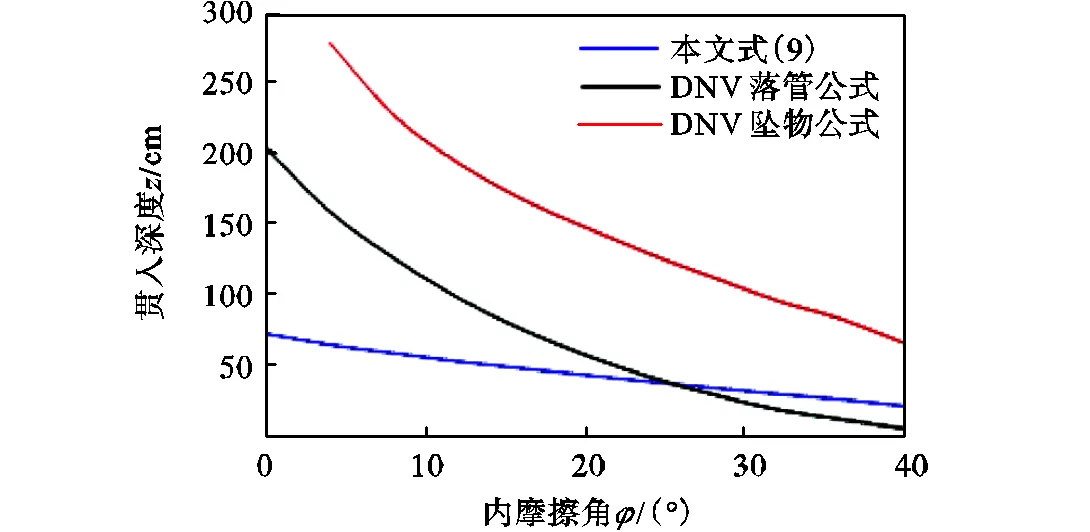
图15 由式(9)~(11)分别计算的落锚贯入深度与内摩擦角之间的关系
4 结 论
(1) 在船舶落锚过程中,贯入深度随船锚触底动能的增加而不断增加,但两者呈明显的非线性关系.
(2) 采用能量守恒原理,基于船锚触底动能与地基承载力公式,建立了不同土体中船舶落锚贯入深度的理论计算方法.通过室内模型试验与现场试验,验证了该方法的可靠性.
(3) 建立了模拟船舶落锚过程的动力显示算法,并将试验数据与数值模拟结果进行对比,证明了数值模拟的可行性.
(4) 现场落锚试验揭示,现阶段常用的3种计算落锚贯入深度的公式不适用于确定黏性土中的最大贯入深度.
[1] Wierzbicki T,Suh M S. Indentation of tubes under combined loading[J]. International Journal of Mechanical Sciences,1988,30(3/4):229-248.
[2] 张 磊. 基于船舶应急抛锚的海底管道埋深及保护研究[D]. 武汉:武汉理工大学航运学院,2013.
Zhang Lei. The Research of the Burial Depth and Protection of the Submarine Pipelines Based on the Ship’s Emergency Anchoring[D]. Wuhan:School of Navigation,Wuhan University of Technology,2013(in Chinese).
[3] 李 庆,马坤明,王凤莲,等. 穿越航道的海底管道保护设计抗锚害分析研究[J]. 中国造船,2013,54(增1):101-106.
Li Qing,Ma Kunming,Wang Fenglian,et al. Analysis of resistance to anchor damage in protection design of subsea pipeline at shipping lanes[J]. Shipbuilding of China,2013,54(Suppl 1):101-106(in Chinese).
[4] Det Norske V. Recommended Practice DNV-RP-F107 Risk Assessment of Pipeline Protection[M]. Norske:Det Norske Verttas,2010.
[5] 雷震名,谭红莹,龚海潮,等. 基于能量法的跨航道海底管线抗落锚实验研究[J]. 水道港口,2015,36(3):272-276.
Lei Zhenming,Tan Hongying,Gong Haichao,et al. Energy method-based experimental research on crossing sub-sea pipeline protection by rockfill against anchors[J]. Journal of Waterway and Harbor,2015,36(3):272-276(in Chinese).
[6] 李学东,李亚斌,陈 伟. 船锚触底贯穿量计算方法[J]. 中国航海,2016(1):85-87.
Li Xuedong,Li Yabin,Chen Wei. Penetrating depth of anchor into seabed[J]. Navigation of China,2016(1):85-87(in Chinese).
[7] 王 懿,贾 旭,黄 俊,等. 基于 CEL 的船舶抛锚入泥深度分析[J]. 石油机械,2014,42(12):44-47.
Wang Yi,Jia Xu,Huang Jun,et al. Analysis of penetration depth of dropped anchor based on CEL[J]. China Petroleum Machinery,2014,42(12):44-47(in Chinese).
[8] 肖 鹏. 海底电缆抛石保护层抗锚害能力分析[D]. 武汉:华中科技大学土木工程与力学学院,2012.
Xiao Peng. The Analysis on the Degree of Submarine Cable Protection by Rockfill against Anchors[D]. Wuhan:School of Civil Engineering and Mechanics,Huazhong University of Science and Technology,2012(in Chinese).
[9] 邱长林,王 菁,闫澍旺. 冲击荷载作用下有碎石保护结构的海底管线DEM-FEM联合分析研究[J]. 岩土工程学报,2015,37(11):2088-2093.
Qiu Changlin,Wang Jing,Yan Shuwang. Coupled DEM-FEM analysis of submarine pipelines with rock armor berm under impact load[J]. Chinese Journal of Geotechnical Engineering,2015,37(11):2088-2093(in Chinese).
[10] 韩聪聪,陈学俭,刘 君. 霍尔锚抛锚深度模型试验研究[J]. 海洋工程,2018,36(5):90-98.
Han Congcong,Chen Xuejian,Liu Jun. Model tests on penetration depth of hall anchor[J]. The Ocean Engineering,2018,36(5):90-98(in Chinese).
[11] 陈 峰,汪嘉钰,别亦白,等. 不同土质条件下大抓力锚的落锚深度研究[J]. 港工技术,2017,54(5):43-48.
Chen Feng,Wang Jiayu,Bie Yibai,et al. Study on penetration depth of high holding power anchors under different soil conditions[J]. Port Engineering Technol-ogy,2017,54(5):43-48(in Chinese).
[12] 国家技术监督局. GB/T 546—1997 霍尔锚[S]. 北京:中国建筑工业出版社,1997.
State Bureau of Technical Supervision of the People’s Republic of China. GB/T 546—1997 Hall Anchor[S]. Beijing:China Architecture and Building Press,1997(in Chinese).
[13] 国防科学技术工业委员会. CB/T 3972—2005 AC-14大抓力锚[S]. 北京:中国建筑工业出版社,2005.
Commission of Science,Technology and Industry for National Defense. CB/T 3972—2005 AC-14 High Holding Power Anchor[S]. Beijing:China Architecture and Building Press,2005(in Chinese).
[14] 谭 箭,李恒志,田 博. 关于事故性抛锚对海底管线损害的探讨[J]. 船海工程,2008,37(1):142-144.
Tan Jian,Li Hengzhi,Tian Bo. Discussion on damage of accidental anchoring operation upon the submarine pipelines[J]. Ship & Ocean Engineering,2008,37(1):142-144(in Chinese).
Study of the Penetration Depth of an Anchor in the Dropping Anchor Process
Liu Run,Wang Jiayu,Bie She’an
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
Dropping anchor is the first step in the process of fixing the position for ship anchoring.However,dropping anchor can damage the cable directly.Moreover,the anchor penetration depth has an important effect on the trajectory of dragging anchor,which could affect the safety of the operation of the submarine structure.To protect the submarine cable,the penetration depth needs to be considered in the dropping anchor process.A series of anchor drop tests were conducted to analyze the influence of anchor mass and drop height on the penetration depth of hall anchor and high holding power anchor in cohesive and non-cohesive soils.On basis of the results of the anchor drop test,the theoretical formula of penetration depth was established using the energy method and Terzaghi’s ultimate bearing capacity formula.The explicit dynamic numerical method was used to simulate the dropping anchor experiment.The results of the simulation reveal the relationship between kinetic energy and penetration depth in the dropping anchor process.The field test was conducted to determine the penetration depth of the dropping anchor process in actual conditions.The results of the field test were compared with the results obtained using the theoretical formula proposed in this study,Young’s formula,DNV falling object formula,and DNV falling tube formula.The accuracy of the theoretical formula proposed in this study has been validated through the field test,with the results of the field test consistent with those of the theoretical analysis.The applicable conditions and limitations of other theoretical algorithms are illustrated in the end.
submarine pipeline;dropping anchor;penetration depth;field test
Supported by the National Natural Science Foundation for Distinguished Young Scholars of China(No.51825904).
TU435
A
0493-2137(2020)05-0508-09
10.11784/tdxbz201905051
2019-05-15;
2019-12-06.
刘 润(1974— ),女,博士,教授.
刘 润,liurun@tju.edu.cn.
国家自然科学基金杰出青年科学基金资助项目(51825904).
(责任编辑:刘文革,樊素英)
