频谱替换无拉伸动校正及其应用

董水利

(中海油田服务股份有限公司 物探事业部，天津 300451)

1 引 言

动校正是传统地震数据处理流程中的重要一环，是实现高分辨率水平叠加的基础[1,2]。常规动校正会引起子波拉伸、波形畸变，从而破坏校正之后CMP道集上同相轴的相关性，最终影响叠加剖面的质量。目前，在实际地震资料处理中有效地解决动校拉伸的方法是外切除，即在CMP道集上对拉伸率大于某个百分比的数据进行外切。这种方法对于浅层地震数据来说，使得大部分地震数据被切除掉[3]，导致浅层地震覆盖次数降低，从而影响了地震数据的信噪比[4-6]。另一方面，大偏移距数据对于地震AVO现象分析至关重要，外切除必然会影响AVO分析效果[7-9]，进一步对后续针对各向异性的研究产生影响[10-13]。在基于一维地球模型的地震记录中，反射同相轴呈现双曲线的形式。动校正的目的是将非零偏移距的地震道变换到零偏移距位置，基于相似原理的方法通常用于计算NMO速度。用于CMP道集的传统动校正产生了随偏移距增加且随零偏移距时间降低的拉伸现象，这也是常规动校正方法的缺陷。针对反射地震数据的动校正拉伸现象一直是讨论热点。为此，Causse等[14]提出了一种针对地震反射旅行时的大偏移距近似框架，Taner等、AI-Chalabi、Gidlow等使用了一种高于2阶的校正方程[15-17]；de Bazelaire提出了一种可移动的双曲线方法[18]，在该方法中扫描参数是双曲线的聚焦时间而非NMO速度。Rupert等引入了block-move-sum(BMS)思想[19]，将静态位移应用于数据块然而再求和，BMS已经成为一种新的研究方向。Perroud等提出一种无拉伸动校正[20]，它可以自动避免动校正拉伸。

本文根据Lichman提出的基于相位的动校正思想[21]，阐述一种高保真无拉伸动校正技术，其基本思想为针对CMP道集直接进行无拉伸动校正。对于动校正拉伸而言，CMP道集中零偏移距道具有最高的频率成分，借用该道的相位谱，保持其他道的振幅谱不变进行动校正。合成例子和实际地震数据处理结果表明，频谱替换方法最大程度保留了大偏移距地震道的信息，同时没有降低同相轴的频率成分，而且可以校正其他因素引起的同相轴非相似性，最终实现了地震数据的同相叠加，有效改善了地震数据的品质，对于后续针对AVO的分析奠定了良好的基础。

2 方法原理

传统褶积模型可以将一个地震道表示为子波与反射系数的褶积，即：

(1)

式(1)中，w(t)表示地震子波；rn表示第n层反射系数；tn为第n层反射系数的旅行时；N表示总地层数。

对式(1)进行傅里叶变换得到：

S(ω)=W(ω)R(ω)

(2)

式(2)中，W(ω)为w(t)的频谱，即

W(ω)=|W(ω)|e-iφ0(ω)

(3)

R(ω)为反射系数的频谱，即

(4)

将方程(4)展开，可以得到：

(5)

(6)

式中，tm为第m层反射系数的旅行时。

根据地震子波和反射系数的振幅和相位谱，可以得到：

|s(ω)|=|W(ω)||R(ω)|

(7)

φ(ω)=φ0(ω)+φR(ω)

(8)

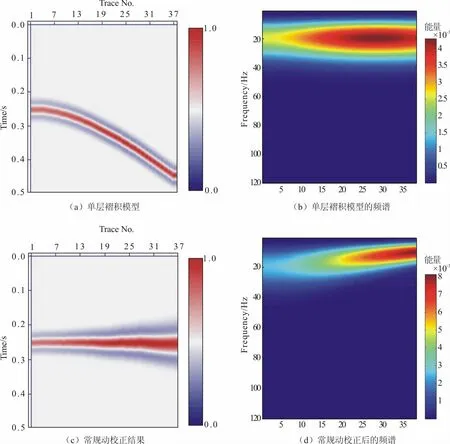
图1 单一同相轴和常规动校正及其频谱Fig.1 The single-event and its traditional NMO seismic profile and spectrum

假设地震子波一定，则振幅谱|s(ω)|和相位谱φ(ω)均与反射系数rn有关。此外，振幅谱|s(ω)|还和反射旅行时组合(tn-tm)有关，但与到达时间无关；而相位谱φ(ω)和反射旅行时tn有关，与反射旅行时组合(tn-tm)无关。方程(8)表明地震道的相位是子波相位和反射系数相位之和。子波的相位决定子波的波形，反射系数的相位包含了同相轴的位置信息。取零偏移距道的相位谱替换其他偏移距道的相位谱，同时振幅谱保持不变，就可以将整个CMP道集在频率域校正为自激自收道集，最后进行反傅里叶变换得到动校正后的时间域道集。

3 理论模型分析

3.1 单一同相轴例子

图1(a)所示为基于单一水平介质模型得到的CMP道集，其中地震子波为25 Hz的Ricker子波，采样率为2 ms，共40道接收。图1(b)为图1(a)的频谱，从图中可以看出不同道之间的频带宽度是一致的。图1(c)为常规动校正后的结果，偏移距越大，子波拉伸越严重，图1(d)的频谱也说明了随着偏移距的增大，远道数据的主频向低频方向移动。

图2(a)为频谱替换法得到的无拉伸动校正结果，该同相轴不存在动校正拉伸现象，而且不同道的子波波形得到了很好保持。图2(b)是图2(a)对应的频谱，从图中可以看出，频谱替换法动校正得到的频带宽度和原始模型的频带宽度一致。

图2 单一同相轴频谱替换动校正结果及其频谱Fig.2 The single-event profile after spectral borrowing NMO and its spectrum

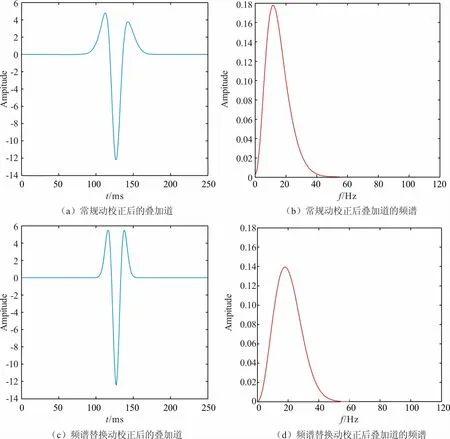
图3 常规动校正和频谱替换动校正后的叠加道及其频谱Fig.3 Comparison of the stack trace and their spectrum using traditional and spectral

为了进一步对比传统动校正和频谱替换无拉伸动校正，现将上述两种动校正的结果分别进行叠加，其叠加道如图3所示，其中图3(a)为常规动校正之后的叠加结果，图3(b)为其对应的振幅谱，图3(c)为频谱替换法动校正之后的叠加结果，图3(d)为图3(c)对应的振幅谱。显然，频谱替换法动校正实现了同相叠加，其波形比传统动校正的规整，能量更加集中收敛，这一点也可以从振幅谱上得到验证。常规动校正叠加道的主频向低频方向移动，频带变窄，而频谱替换方法中同相轴主频并未降低，且其频带较宽。由此可见，频谱替换动校正得到的叠加结果分辨率更高，保幅性更佳。

3.2 多个同相轴例子

图4(a)为含三个同相轴的CMP道集。保持每道的振幅谱不变，用参考道的相位谱替换所有道的相位之后得到的动校正结果如图4(b)所示，显然动校正之后没有明显的拉伸现象。

为了进一步验证本文方法的抗噪能力，对图4(a)加入一定的随机噪声后得到图5(a)，图5(b)为其频谱替换动校正之后的结果。由图5可见，随机噪声对本文方法的影响较小，在这种情况下同样可以得到分辨率较高的动校正结果。

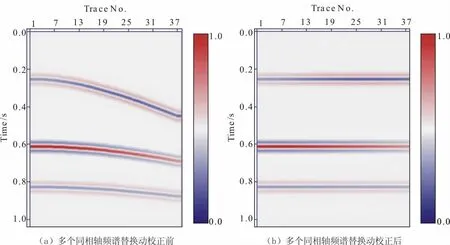
图4 多个同相轴频谱替换动校正前后结果Fig.4 Multi-event seismic data and its spectral borrowing NMO profile

图5 含噪多个同相轴频谱替换动校正前后结果Fig.5 Noisy multi-event seismic data and its spectral borrowing NMO profile

4 实例分析

图6为从实际地震数据中抽取一个CMP道集且截取其中的一段，该数据最小偏移距为0 m，最大偏移距为2 500 m，有效记录长度为2.0 s。图7(a)为常规动校正之后的CMP道集，图7(b)为频谱替换动校正后的CMP道集。由图7可见，与常规动校正相比，频谱替换动校正较好地避免了动校拉伸的影响，远道同相轴得到有效保留，同时消除了其他因素引起的剩余动校正量，校正后的地震数据同相性更佳，对于后期的AVO分析具有重要的意义。

图7 实际数据常规动校正Fig.7 Comparison of the real seismic data using traditional and spectral borrowing NMO respectively

5 结 语

本文呈现了一种无拉伸的动校正方法，它借用零偏移距道的相位谱，保持其他道的振幅谱不变进行动校正。频谱替换方法最大程度保留了地震数据中浅层大偏移距地震道的信息和同相轴中的高频成分。合成例子和实际数据处理结果表明，文中实现的方法可以有效增加CMP道集中浅层远道的叠加次数，实现了地震数据的同相叠加且抗噪声能力较强，有利于改善地震数据的品质，对于后续的AVO处理和属性反演具有重要的意义。