基于全相位FFT的电磁法有效相位信息提取
2020-04-26李帝铨胡艳芳汪振兴苏煜堤
李帝铨,王 涵,胡艳芳,吴 桐,汪振兴,苏煜堤
(1.中南大学 有色金属成矿预测与地质环境监测教育部重点实验室,湖南 长沙 410083;2.中南大学 有色资源与地质灾害探测湖南省重点实验室,湖南 长沙 410083;3.中南大学 地球科学与信息物理学院,湖南 长沙 410083)
1 引 言
电磁场的振幅和相位与地下介质的电阻性和电感性密切相关。理论研究表明,电磁场的振幅和相位是可以相互转换的,它们所包含的地质信息量是相同的,但相位曲线相比于振幅曲线,变化幅度更大,因此在一定地质条件下相位具有更高的分辨能力。
实际勘探中,电磁法资料往往含有大量的电磁干扰[1,2],导致难以准确拾取相位信息,因此,国内外众多学者开展了相位测量研究。相位测量的主要方法为模拟和数字方法两种,由于数字方法成本低、适应强、灵活度高,相位的测量逐渐向数字化方向发展。现阶段数字测相法主要有相关分析法、希尔伯特变换法、正弦曲线拟合法、快速傅里叶变换(FFT)等[3-5],它们各有优缺点。
数字相关法在理论推导上和信号的频率无关,所以对未知频率的信号可以进行相位差测量,适合高频正弦信号相位差的测量;可以有效抑制噪声干扰。但是对于相关性强的干扰信号和谐波干扰,数字相关函数法在低信噪比下,测量误差较大,只能测量正弦或余弦信号,对一般的周期信号无法测量。所以,数字相关法约束条件多需预知信号频率且难以消除谐波干扰,分辨力受采样间隔限制。希尔伯特变换使得对短信号和复杂信号的瞬时参数的定义及计算成为可能,能够实现真正意义上的瞬时信号的提取,然而,希尔伯特变换法对“同步采样”要求较高,近似应用于窄带信号且只处理任何时刻为单一频率的信号。正弦拟合法需要选择适合的条件,拟合耗费大量时间。这些方法共同的缺点在于抗噪能力差,影响了他们在电磁法数据处理中的应用效果[6]。
FFT方法是在数字化测量相位中比较常用的手段,其变换结果为复数,含有丰富的相位信息,运算效率高,相位测量可以克服时间间隔测量对随机噪声、谐波失真和零点漂移等比较敏感的缺陷,相较于相关分析法、希尔伯特变换法、正弦曲线拟合法,更加适合用于电磁相位信息的提取[7-12]。但FFT也存在两个缺点:①频谱泄漏会降低相位测量的精度;②需要严格的“同步采样”[13-15]。
综上所述,在实际应用中,以加窗FFT为代表的相位测量算法存在抗噪能力差,相位信息难以精确提取的问题,导致相位信息难以利用。为了准确拾取相位信息,需要做到:①提高频谱泄漏抑制能力;②不受“同步采样”约束;③不受频率偏离影响;④增加抗噪能力。
2 全相位FFT测相法
全相位数字信号处理是王兆华和侯正信提出的一种数字信号处理的新方法。2003年王兆华首次提出了“全相位谱分析(all-phase FFT,简称apFFT)”的概念,全是指整体,相位是指局部,是最大程度上进行重叠处理的方法[16]。全相位FFT方法是在离散傅里叶变换基础上提出的测量相位的新方法,几乎不受频率偏离影响,具有更优良的抑制频谱泄漏性能,具有“相位不变”性,不需“同步采样”就能获得较为精确的相位信息,解决了以加窗FFT为代表的相位测量算法存在的问题,适用于电磁相位信息提取。
2.1 全相位FFT原理
全相位FFT主要是对输入数据按照设计需求进行不同加权后,以中心数据作延拓重复处理,得到新的序列再进行FFT变换的方法。
例如一个信号序列为:
(1)
选取长度N=3的信号进行处理:
2.1.1 选取所有包含中心数据x(0)且长度N=3的序列
x0:x(0)x(1)x(2)
x1:x(-1)x(0)x(1)
(2)
x2:x(-2)x(-1)x(0)
2.1.2 进行序列的周期延拓
(3)
2.1.3 竖直方向求和,形成新的序列
(4)
则新序列为:
(5)
2.1.4 把新序列式进行FFT变换
上述过程可以简化为图1的处理流程:输入信号经过相应延迟后对其进行数据加权,将间隔为N的数据两两叠加(中心数据除外)形成新的数据序列,再进行FFT就得到了apFFT的结果。
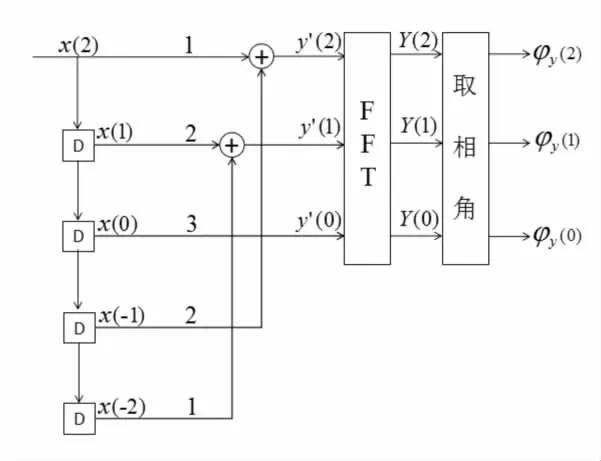
图1 全相位FFT频谱分析等效框图(N=3)Fig.1 Equivalent diagram of all-phase processing (N=3)
2.2 传统FFT与全相位FFT测相方法
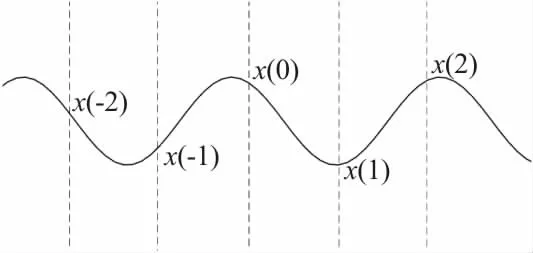
图2 全相位FFT的中心样点相位估计Fig.2 Phase center sampling estimation of all phase FFT
传统FFT与全相位FFT测相位利用的信号序列长度是不一样的,继续以上文信号序列为例:为估计样点x(0)的相位值,传统FFT法是选取x(0)到x(2)之间的N=3个数据来做FFT变换(图2),而全相位方法是选取了以x(0)为中心数据利用x(-2)到x(2)的2N-1=5个子数据,通过全相位的叠加选取主区间N=3个数据来进行FFT,这样通过2N-1个数据进行叠加处理选取主区间数据的FFT变换使得频谱有“全相位不变”的特性:主谱线上的相位谱值等于输入序列的中心样点相位的理论值,相位主线谱附近呈平坦状,可降低频率偏离的影响。下面将通过两个例子来说明其性质。
2.2.1 例1
给定一个信号y由频率为11 Hz、24 Hz、35 Hz、65 Hz的余弦复合而成,采样频率为256 Hz,采样点数为256,频率分辨率为1 Hz(即谱线k对应于相应的频率f,各自初始相位值为:30°、45°、60°、90°。
(6)
相应的传统加汉宁窗FFT和加汉宁窗apFFT相位谱如图3所示。通过选取两种方法的相位谱主线谱线处(k=11、24、35、65)的相位值,可得到apFFT和传统FFT方法的相位谱值(表1)。
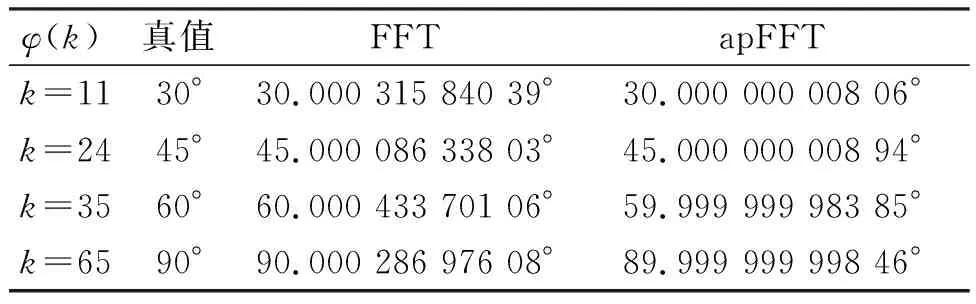
表1 apFFT和传统FFT方法的相位谱值结果对照
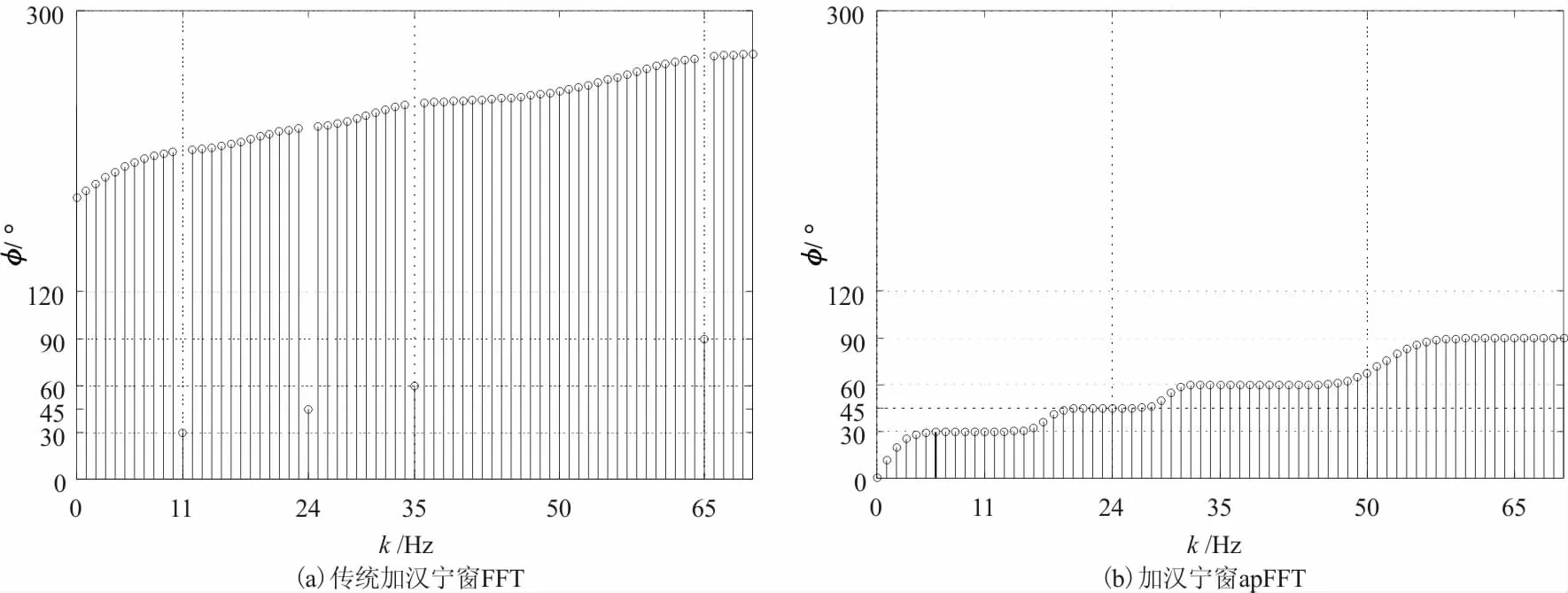
图3 多频余弦信号传统加汉宁窗FFT和加汉宁窗的apFFT相位谱Fig.3 FFT and apFFT phase spectrum of multifrequency cosine signal
从图3的相位谱可看出两者有着明显的差别,传统加汉宁窗FFT的相位谱值在其主谱线附近呈现跃变的“凹”状,只有在对应的主谱线相位谱值才准确,相位值的精度为10-5。而apFFT相位谱曲线比较平坦,在k=11、24、35、65处,测量的相位值与真实值30°、45°、60°、90°几乎完全一致,精度高达到了10-9。且在主谱线周围谱线上的相位值都非常接近于初相位值,这是“相位不变性质”的突出表现。
2.2.2 例2
给定信号y由频率为11.3 Hz、24.2 Hz、35.2 Hz、65.1 Hz的余弦复合而成,采样频率为256 Hz,采样点数为256,频率分辨率为1 Hz(即谱线对应于相应的频率f,各自初始相位值为:30°、45°、60°、90°:
y=3cos(2π×11.3×t+π/6)
+4cos(2π×24.2×t+π/4)
+4cos(2π×35.2×t+π/3)
+2cos(2π×65.1×t+π/2)
(7)
频率发生如式(7)所示的偏离时,相应的传统加汉宁窗FFT和加汉宁窗的apFFT相位谱如图4所示。通过选取两种方法的相位谱主线谱线处(k=11、24、35、65)的相位值,可得到apFFT和传统FFT方法的相位谱值结果(表2)。
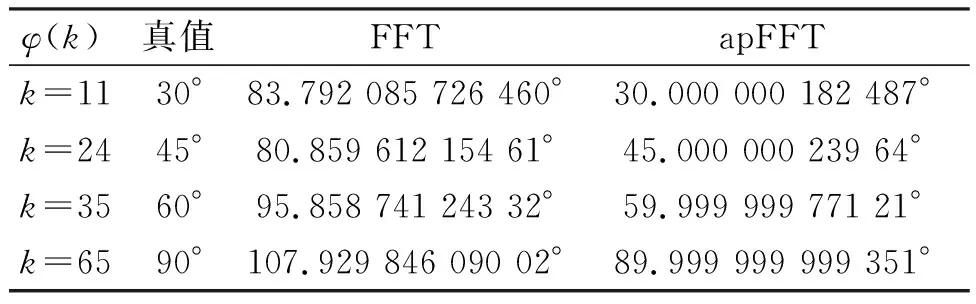
表2 频率发生偏离时apFFT和传统FFT方法的相位谱值结果对照
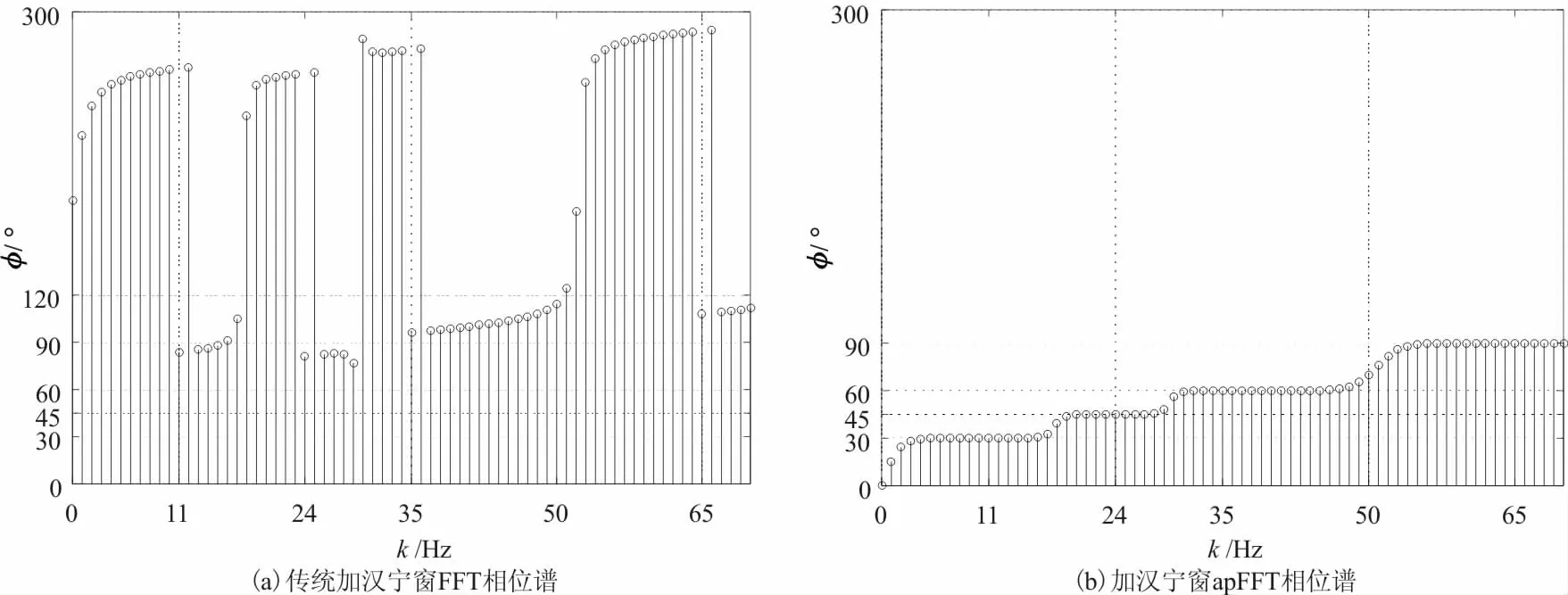
图4 频率偏离时传统加汉宁窗FFT和加汉宁窗的apFFT相位谱Fig.4 apFFT and FFT phase spectrum of cosine signal when the frequency deviates from the expected value
由图4和表2可知,在频率发生偏离时,传统的FFT相位谱曲线很乱,不能获取准确的相位值,测量的相位值与真实值的偏离很大,这是由于“不同步采样”情况导致测出的相位不准确;反观apFFT的相位谱却很平坦,且测量精度达到了10-7,这样的精度意味着apFFT无需通过任何的校正措施从主谱线上就可得到高精度的初相位估计值。
由表1和表2可知,apFFT法测量信号相位初值精度高,没发生频率偏离时比传统FFT高5个数量级,给定的信号频率偏离时几乎不受信号频率偏离的影响,这说明apFFT不需要“同步采样”,不需校正就获得较准确的信号初始相位值,这就是apFFT方法“相位不变性”的突出特征。apFFT方法的“相位不变性”不但能准确获得相位信息,还能通过apFFT相位差来进行频谱校正,能更加准确地获得干扰条件下的电磁信号相位信息。
3 仿真实验
电磁法的信号往往会受到各种噪声的干扰,噪声大致分为:场源噪声、地质噪声、人文噪声和随机噪声,当噪声同信号混叠在一起的时候很难将二者区分开来[17,18]。
电磁法的典型噪声干扰有:类脉冲噪声、类充放电三角波噪声、类方波噪声、类阶跃噪声、工频噪声这几种[2,19,20]。仿真在这几类典型的噪声条件下来测量相位,可有效地分析apFFT方法在噪声条件下的应用效果。
3.1 apFFT测相的抗噪性能
为验证apFFT测量相位的抗噪性能,将apFFT与传统的加窗FFT方法测得的相位结果进行比较。
实验将谱分析的采样点数N取2 048,采样频率2 048 Hz,两个如式(8)所示的余弦叠加作为信号,在Matlab中产生仿真信号,在信号中加入三角波、矩形波、阶跃波、10 dB高斯白噪、脉冲噪声等,对比两种方法提取电磁信号相位的性能。
(8)
分别采用传统FFT方法和apFFT方法获取20 Hz余弦信号频率无偏离和频率发生偏离时在不同噪声条件下的相位值,获得的谱值见表3和表4。

表3 分别加入相应噪声条件下的相位值(k=20)

表4 加入10 dB高斯白噪的情况下传统FFT和apFFT的对比(k=20)Table 4 Comparison of FFT and apFFT with 10 dB Gaussian white noise (k=20)
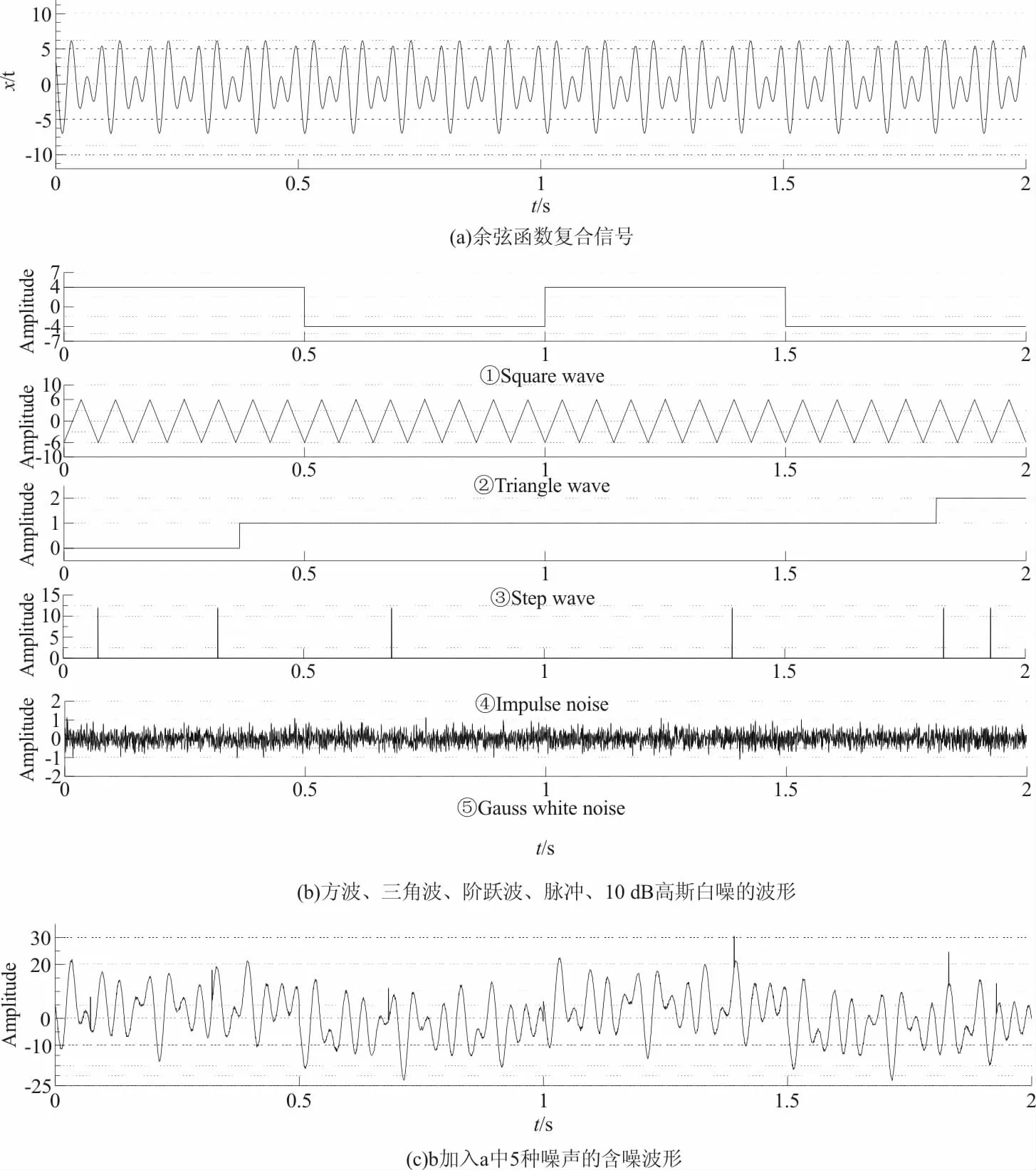
图5 纯信号源波形、噪声的波形、加噪信号波形Fig.5 Waveforms with pure signal, noise and noise signal
在三角波、方波、脉冲、阶跃波噪声条件下传统的FFT测量的相位值较为准确,但发生频率偏离时测量的相位值误差较大。在相应噪声干扰下(表3)apFFT测量相位的精度比传统FFT高,发生频率偏离时能获得较为准确的相位值。并且在加入三角波、方波、脉冲、阶跃波噪声的基础上加入高斯白噪声条件(表4),得到apFFT与FFT的对比结果,apFFT依旧能获得较准确的相位值,其相位测量误差小于1 %。
3.2 apFFT在噪声条件下测相区分有效信号能力
为验证apFFT区分有效信号的能力,在仿真信号中加入了信噪比为25 db的高斯白噪声、三角波、方波噪声,采样点数依旧为2 048,采样频率为2 048 Hz,采样分辨率为1 Hz。
仿真信号为:
(9)
式中,f为变量,通过apFFT方法分别获取f=20 Hz、20.5 Hz、21 Hz、22 Hz、23 Hz时的相位谱值,来分析apFFT在无噪和有噪条件下区分有效信号的能力。获得的相位谱如图6所示,主谱线的相位值列于表5和表6。

表5 未加入噪声主谱线(k=20)周围的相位谱值

表6 加入噪声主谱线(k=20)周围相位谱值
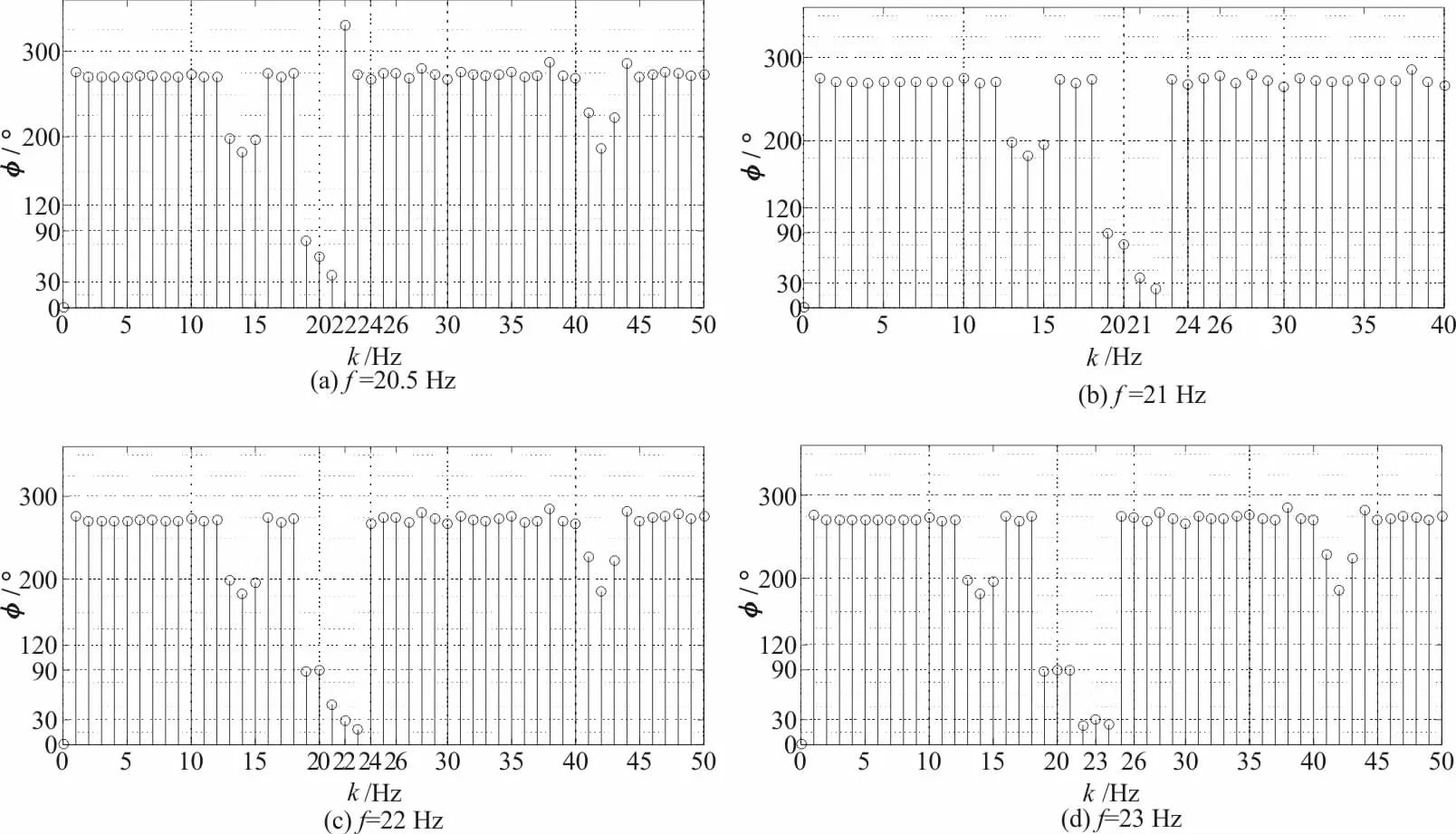
图6 20 Hz余弦信号时不同频率下的apFFT相位谱Fig.6 apFFT phase spectrum of 20 Hz cosine signal with different frequency components
由表5和表6可知,在频率分辨率为1 Hz时,没有噪声条件下apFFT方法在相差2倍频率分辨率情况下就精确获取20 Hz和22 Hz的有效信号相位值;当在噪声条件下信号的频率相差3倍频率分辨率时才能获取较好的有效信号相位值。由于“相位不变”的特性,当有效信号频率间隔变大时apFFT的相位谱平坦程度(图6)变好,主线谱处的值由跃变而变得平坦,因此平坦程度受到噪声和有效信号间隔的影响。
全相位apFFT方法受到典型噪声干扰影响下区分有效信号的能力较好,区分的能力会受到噪声影响,但由于“相位不变”特性使得其受到影响较小。由于电磁法工程勘探中易受到典型噪声干扰影响,因此初步判断电磁法工程勘探中运用apFFT方法拾取相位信息能取得好的效果。
4 结 论
本次研究将apFFT和传统FFT进行对比分析,得到以下结论:
1)apFFT法具有传统加窗FFT法所具有的优点,能有效地抑制高斯噪声,对电磁法典型的干扰波噪声有着良好的抑制效果。
2)apFFT测量的相位谱值无须校正措施就有着很高的精确度,“相位不变性”有着几乎不受频率偏离影响的特性,相位精度高于传统加窗FFT法,且测得的是数据的瞬间相位,不需要参考波形。
3)apFFT测相在干扰条件下区分有效信号能力比较好,能有效地在频率密集的时候区分有效信号。
4)apFFT方法处理数据简单、计算量较小、测量精度较高,对于拾取有效的电磁法相位信息具有广泛的应用前景,下一步将对电磁法相位信息提取做进一步试验。
