基于修正G1和Vague集的川藏铁路重大桥梁桥位评价研究
2020-04-26邱钰峻李远富但鹏飞
邱钰峻,李远富,柯 斌,但鹏飞
(1.西南交通大学土木工程学院,成都 610031; 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)
为实现国内互联互通,加快西部建设,我国大量规划建设渝利铁路、成兰铁路、川藏铁路等艰险山区铁路。而川藏铁路穿越地区具有大高差、高海拔、地质灾害频发、气候恶劣多变、生态环境脆弱等特点[1],其线路选择与建设都面临着巨大挑战。其中,艰险山区地形地质条件下桥位的选择将严重影响线位、工程投资和运营维护[2],特别是对于跨越深切沟谷的大渡河、雅砻江、金沙江、澜沧江、怒江等大江大河的重大桥梁,其桥位选择尤为重要。
川藏铁路选线以“减灾”[3]为主要理念并注重“绿色生态”[4],桥位选择以“一般大桥就线,重大桥梁就桥”为原则[2]。目前对桥梁方案评价的研究多从地质水文[5]、边坡稳定性[6-7]、施工条件[8]、河道演变[9]等方面综合指导桥位选择,但对于地质条件复杂、气候恶劣、生态脆弱的川藏铁路桥位选择缺乏全面性评价和系统性决策方法。另一方面,目前对多属性方案评价的研究热点集中在赋权方法和排序方法两方面。关于赋权方法的研究,多对各种主观权重(层次分析法[10]、Delphi法[11]、G1法[12]等)和客观权重(变异系数法[13]、熵权法[14]、CRITIC法[15]等)进行修正或对其组合方式进行改进,以获得更合理的指标综合评价。其中,主观赋权G1法作为对层次分析法的改进,能避免计算复杂、一致性检验难以通过的问题[16];客观赋权CRITIC法能同时反映指标信息量的大小和指标间的相关性[17];通过客观修正主观组合赋权能更合理地兼顾专家意见和数据信息[18],有效提高对川藏铁路重大桥梁桥位多属性综合评价的合理性。而对于排序方法的研究,多在传统排序方法灰色关联法和TOPSIS法的基础上进行改进[19]。其中,TOPSIS法比灰色关联更能体现方案整体的优劣[20],而Vague集能有效反映评价的模糊性和不确定性[21],将TOPSIS法向Vague集拓展进行排序,对川藏铁路桥位选择这样的复杂模糊系统评价具有良好的适用性。
因此,对艰险山区铁路重大桥梁桥位选择进行研究,选取工程技术、工程经济、施工条件、地形地质、水文气候、生态影响6个方面指标建立起川藏铁路重大桥梁桥位选择指标评价体系,以CRITIC法修正G1法进行指标主客观组合赋权,并采用Vague集-TOPSIS法进行方案排序确定最优桥位方案。
1 川藏铁路桥位选择指标评价体系
川藏铁路沿线沟谷深切、坡体稳定性差、断层广布、生态脆弱,且其降水和极端气温随高程变化极大。一方面川藏铁路地质灾害频发,影响桥梁线路安全;另一方面极端气候严重影响桥梁耐久性和施工条件。因此,川藏铁路重大桥梁桥位选择应以“减灾”为核心,在保证桥梁及线路安全性的情况下,兼顾环保性和经济性。根据川藏铁路重大桥梁选址原则[2]并结合川藏铁路沿线特征,选取技术可行性、行洪要求、通航要求3个指标作为桥梁修建的可行性判断指标;从工程技术、工程经济、施工条件、地形地质、水文气候、生态影响6个方面遴选出17个指标建立川藏铁路重大桥梁桥位方案综合评价的指标体系,如图1所示。
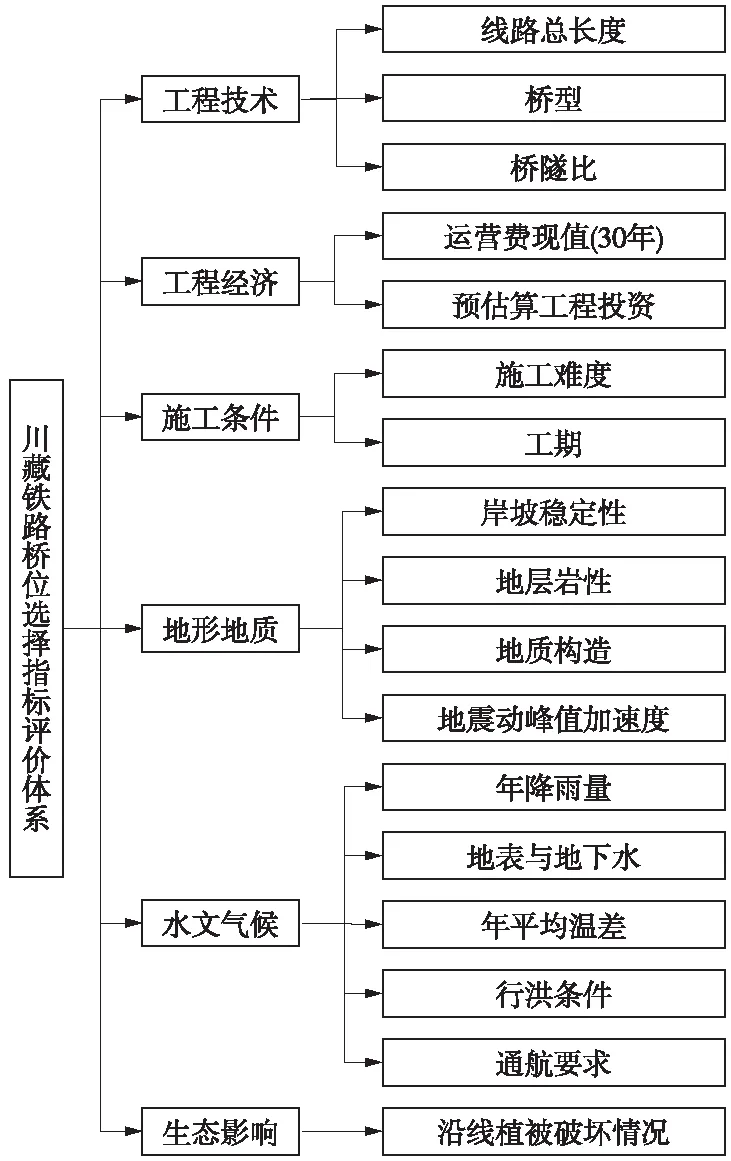
图1 川藏铁路桥位选择指标评价体系
2 基于CRITIC-G1法的指标赋权
2.1 CRITIC法客观赋权
CRITIC法是根据指标数据的差异性和各指标间的相关性确定客观权重,其计算步骤如下。
(1)计算指标Xj的标准差σj
(1)
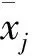
(2)计算指标Xi与指标Xj相关性rij
(2)
(3)计算指标Xj所含信息量cj
(3)
(4)计算客观权重wC
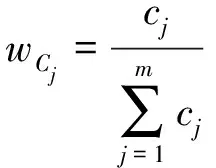
(4)
2.2 G1法主观赋权
G1法是通过专家确定m个指标的重要度排序及相邻重要度排序指标间的比值确定主观权重wG,其计算公式如下

(5)
wGj-1=rjwGj,j=m,m-1,…,3,2
(6)
式中,rj为专家确定的第j-1重要指标与第j重要指标的重要度比值;wGj为第j重要指标的主观权重。
2.3 CRITIC修正G1法
主观赋权的主观意愿过强,客观赋权又难以表征指标本身的重要性。因此,需组合主客观权重进行赋权,以提高指标综合评价的合理性。而采用客观修正主观的组合赋权方式能使评价结果具有更好的合理性和区分度[18],因此采用CRITIC修正G1法进行组合赋权,用CRITIC法计算所得指标信息量之比代替G1法中有专家确定的指标重要度之比,以巧妙兼顾指标客观信息量和主观重要度。则相邻重要度排序指标间的比值rj修正为[12]

(7)
3 川藏铁路桥位评价模型
3.1 Vague集
Vague集作为模糊集的发展,通过构建隶属区间[tA(xi),1-fA(xi)]以同时表示论域U={x1,x2,…,xm}中元素xi对于Vague集A位于[0,1]区间的真隶属度tA(xi)、假隶属度fA(xi)和犹豫度πA(xi)=1-tA(xi)-fA(xi)。
3.1.1 指标的Vague集表示
定性指标可根据Vague集7级语言变量(表1)确定方案集A={A1,A2,…,An}中各定性指标对应Vague值。
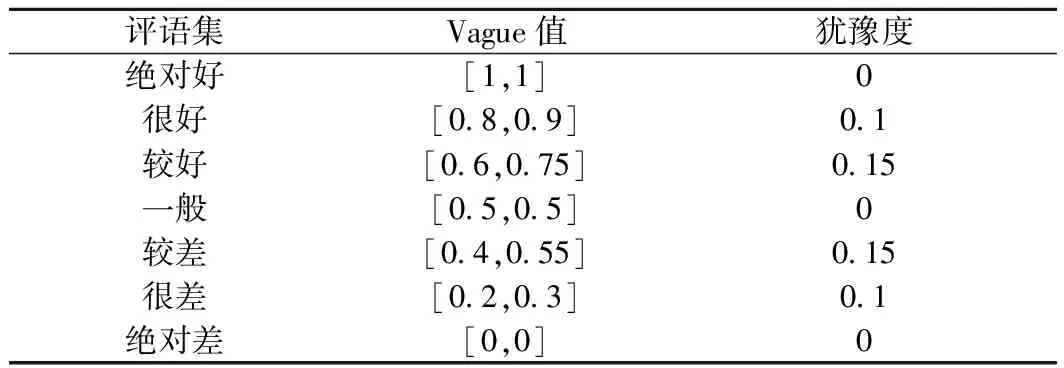
表1 Vague集7级语言变量
定量指标可分为成本型和效益型指标,分别可根据式(8)、式(9)转化为Vague集值。
成本型
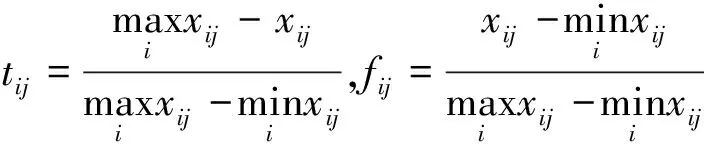
(8)
效益型

(9)
式中,tij、fij分别为方案Ai在指标Xj下的真、假隶属度;xij为方案Ai在指标Xj下的指标初始值。
最终将方案Ai在指标集X={X1,X2,…,Xm}下的Vague集表示为
Ai={(X1,[ti1,1-fi1]),(X2,[ti2,1-fi2]),
…,(Xm,[tim,1-fim])}
(10)
3.1.2 Vague集的适应度及指标权重
通过Vague集对方案指标模糊度的量化,可进一步对每个指标的不确定性信息进行处理,得到方案各指标适应度,对指标进行较为准确的描述。高建伟公式[22](式(11))能合理利用未知信息,评价稳定可靠,鲁棒性好[23],对川藏铁路桥位指标模糊评价具有很好的适用性。因此,采用式(11)将方案指标Vague集转化为适应度矩阵H=(hij)n×m
(11)
式中,hij为方案Ai在指标Xj下的适应度。
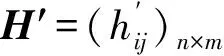
(12)
根据适应度归一化矩阵H′,利用式(1)~式(3)、式(5)~式(7),即采用CRITIC修正G1法计算得到指标综合权重W。
3.1.3 Vague集的相似度量
对于方案的Vague集多准则模糊决策,需求解各方案与理想方案的相似度量M(M∈[0,1]),相似度量M越接近1,方案越相似,相似度最高的方案即最优方案。整体求解思路为:先求解两方案各指标Vague值的相似度量,在综合指标权重进行加权得到两方案Vague集的相似度量。
Vague值[tx,1-fx]、[ty,1-fy]间的相似度量需综合考虑3个因素[24]。
(1)表征真隶属度和假隶属度差异的区间端点距离,即|tx-ty|和|fx-fy|;
(2)表征真假隶属趋势对比的Vague值核距离(S(x)=tA(x)-fA(x))对比,即|S(x)-S(y)|;
(3)Vague值中犹豫度πx、πy对真假隶属度的影响[24]。
邓维斌[25]公式综合考虑上述3个因素,度量结果符合实际且具有很强相似度区分能力。因此,选取此公式计算Vague值的相似度量M([tx,1-fx],[ty,1-fy]),即
M([tx,1-fx],[ty,1-fy])=

(13)
结合CRITIC修正G1法,计算得到指标综合权重W,进行指标Vague值相似度量加权,得到Ai、Aj两方案Vague集的相似度量为
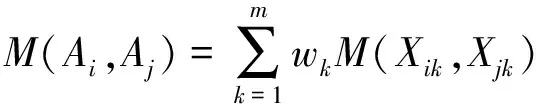
(14)
3.2 基于TOPSIS-Vague集的方案排序
TOPSIS法通过衡量方案与正理想解和负理想解的距离来确定最优方案,而Vague集能更准确描述定性指标的不确定性,可衡量各方案间的相似度进行多准则模糊决策。将两个方法进行结合,能有效兼顾川藏铁路桥位方案的整体性和内部变化评价。计算步骤如下。
(1)确定方案Vague集的正理想解方案A+和负理想解方案A-

(15)

(16)
(2)根据式(13)、式(14)计算各备选方案Ai(i=1,2…,n)与正理想解方案A+和负理想解方案A-的相似度量M(Ai,A+)、M(Ai,A-),相似度量越大,则备选方案与理想方案的距离越近。
(3)结合TOPSIS法计算方案Ai(i=1,2…,n)贴近度ei,如式(17)所示。贴近度ei反映了备选方案与正理想解方案A+的相似度在整体正负理想解相似度的占比,其值越大,则备选方案与正理想解距离越近,与负理想解距离越远,整体上方案越优,可将备选方案贴近度值最大者作为最优方案。
(17)
4 怒江大桥案例分析
川藏铁路邦达机场至八宿段需跨越怒江,而怒江沿岸沟谷深切,必须采用大跨度桥梁跨越[2]。怒江大桥的修建困难、技术复杂,属A类重大桥梁工程,且作为川藏铁路的控制点,极具政治、经济和军事意义。因此,需对怒江大桥桥位进行多方案比选,确定最优方案。经过大范围选址,可选桥位有加腊、拉巴、吉卡、麦确、丢攻、麦热等7处,但满足桥位工程地质安全性要求的仅丢攻、加腊两处。根据丢攻、加腊两处桥位地形地质特征,确定了3个满足技术可行性的桥式方案,即采用高760 m、主跨(140+1064+140) m钢桁梁悬索桥的丢攻高桥位方案A1,采用高240 m、主跨500 m高桁拱桥的丢攻低桥位方案A2,采用高640 m、主跨980 m钢桁梁悬索桥的加腊桥位方案A3[2]。重大桥梁作为线路的控制点,其桥位和桥式方案不仅关乎桥梁本身建设难度,还会影响线路工程数量、沿线施工难度、地形地质、水文气候、经济效益、生态等情况。如:加腊和丢攻桥位虽均满足工程地质要求,但加腊桥位线路较丢攻桥位线路沿线地质条件较差,但其桥隧比较低;丢攻桥位,高桥方案较低桥方案能缩短线路长度,但会增加桥隧比。因此需根据川藏铁路桥位选择指标评价体系进行多准则综合评价。由于各方案和各指标间的差异评价具有模糊性,为更准确评价方案间差异,采用基于修正G1-Vague集的评价模型进行3个方案的详细比选,3个方案的指标信息如表2所示。
根据表2指标信息,分别采用Vague集7级语言变量(表1)和式(8)对三个方案的指标值(定量指标均为成本型指标)进行Vague值量化,如表3所示。
以“减灾”为核心,在保证桥梁、线路的基础上,兼顾经济和生态效益,从而确定一级指标重要度排序为X4>X1>X5>X2>X3>X6,各准则层二级指标重要度排序为X11>X12>X13,X22>X21,X31>X32,X41>X43>X42>X44,X54>X55>X52>X51>X53。
再对其指标值无差异的指标进行约简,约简掉地表与地下水X52、行洪条件X54、通航要求X55三个无差异指标。


表2 怒江大桥桥位评价指标

表3 怒江大桥桥位方案Vague集量化
根据式(15)、式(16)确定正理想解方案A+和负理想解方案A-如表3所示。又根据式(13)、式(14)、式(17)计算得3个桥位方案贴近度为:e1=0.584 5、e2=0.472 8、e3=0.408 8。则,方案评价排序为:A1>A2>A3,丢攻高桥位方案A1为最优方案。
3个桥位方案桥梁本身建设难度均较大,三者均需架设缆索吊施工,其中丢攻高桥方案施工场地狭窄,丢攻低桥方案采用钢桁拱桥还需设置扣束、背束,均使施工难度加大。从线路整体上看,丢攻高桥位方案沿线路工程地质条件较好,使线路整体施工难度较小;而丢攻低桥方案和加腊桥位方案均需大量展线,不仅极大增加了隧道长度,增大了工程量,且加腊桥位方案沿线地质条件较差、降雨量大,易发生灾害,还使得线路整体建设难度增加。因此丢攻高桥位方案在工程技术、施工难度、地质条件方面更加安全可靠。丢攻高桥位方案较其他方案缩短线路长度34 km以上,减少预估工程投资57亿元以上,且运营费用较少,工期较短,创造了极大经济和社会效益。由此可见,选择该方案作为最终怒江大桥桥位方案,合理可行,同时也说明该川藏铁路桥位评价模型评价结果的正确性,能通过Vague集较为准确地量化各模糊性评价指标,并结合TOPSIS法进行多准则模糊评价,得到正确结果。
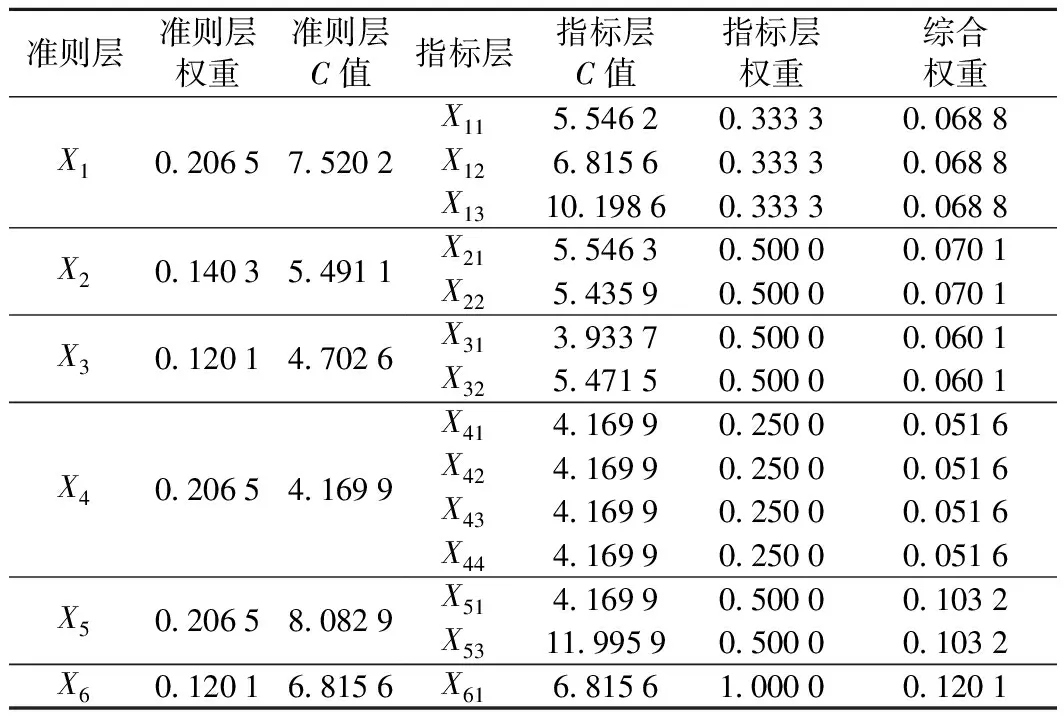
表4 怒江大桥桥位选择指标权重
另一方面,各准则权重不同,而各准则层下各指标权重相同,说明同一准则下的各指标由CRITIC法确定的反映指标方案间差异大小和指标间相关性的指标客观信息量与专家确定的重要度的大小顺序相悖,由此均衡指标权重。可见以信息量之比代替重要度之比修正G1法赋权能兼顾客观差异与主观偏好,提高评价合理性。
5 结论
(1)以减灾为核心,以工程技术、工程经济、施工条件、地形地质、水文气候、生态影响6个方面17个指标建立指标体系,对川藏铁路重大桥梁桥位方案评价更具全面性和针对性。
(2)用指标CRITIC信息量之比代替G1法中主观确定的指标重要度之比修正G1法组合赋权,能兼顾指标客观信息与主观重要性,提高赋权合理性。
(3)用Vague集对川藏铁路桥位指标进行量化,能较有效处理指标评价的模糊性,提高评价准确性,并与TOPSIS结合进行排序,能综合衡量方案的内部相似性和整体相似性。
(4)建立修正G1法和Vague集的桥位评价模型,确定怒江大桥的最优桥位为丢攻高桥方案合理可行,可为艰险山区铁路重大桥梁桥位选择提供有效决策方法。
