轨下新型网孔式弹性垫板力学性能影响研究
2020-04-26翟志浩和振兴张哲远李鹏浩
翟志浩,和振兴,李 斌,张哲远,王 瑶,李鹏浩
(1.兰州交通大学土木工程学院,兰州 730070; 2.兰州交通大学机电工程学院,兰州 730070)
引言
目前,轨道结构主要包括有砟轨道和无砟轨道两种形式。对于有砟轨道而言,轨道结构的弹性主要由道砟提供;但对于无砟轨道,轨道结构的弹性主要由扣件系统的弹性垫板提供。弹性垫板在吸收钢轨的振动能量和缓冲轮轨冲击方面具有重要作用。因此,国内外学者对铁路弹性垫板进行了大量研究。
文献[1-2]对一种铁垫板下新型沟槽式弹性垫板进行了研究,运用有限元软件分析了不同沟槽深度、沟槽宽度、沟槽数目以及材料参数对弹性垫板力学性能的影响,结果表明:该参数对弹性垫板静刚度影响较大。文献[3-4]研究了不同橡胶材料本构模型的特性,结果表明:Mooney-Rivlin本构模型可在中、小应变时,较好地描述橡胶材料超弹性特性。文献[5-7]分析了橡胶弹性垫板力学性能的影响因素,其中包括几何结构、材料特性、扣压力、轮轨力、温变、时变等。文献[8-10]对WJ-8型扣件弹性垫板在低温环境中的刚度和阻尼系数进行研究,结果表明:低温条件对车辆运行平稳性影响较小,但对轮对垂向振动影响较大。文献[11-12]对WJ-7A、WJ-7B扣件的弹性垫板的老化和疲劳性能进行了研究,结果表明:弹性垫板的静刚度随服役时间增长而增加、且环境温度会加速老化。
上述文献均针对传统纵向沟槽型弹性垫板和聚酯垫板进行研究。传统纵向沟槽型轨下弹性垫板(图1)虽然阻尼性能比聚酯材料垫板好[13],但在折角部位应力较高,耐久性较差且材料的弹性利用率较低。文献[14]提出了一种轨道交通高阻尼、位移量可调的弹性垫板结构。其目的是在满足传统弹性垫板基本功能的条件下,充分发挥橡胶材料的弹性,使弹性垫板受力均匀化,可有效降低垫板的应力,提高其耐久性。因此,本文分析了将其应用于扣件系统而衍生出的一种新型网孔式轨下弹性垫板结构(图2)的特性。该结构的关键几何参数为网孔间距b、网孔内接圆直径a2、板厚h和倒角半径r。假定弹性垫板材料参数不变,依次改变4种关键参数,分析其对弹性垫板力学性能的影响,并对网孔结构应用于轨下弹性垫板的可行性进行评价。

图1 纵向沟槽型垫板

图2 网孔式轨下弹性垫板
1 结构与模型
1.1 网孔式弹性垫板结构与模型
根据弹性垫板受力特性,建立了图3所示的网孔式轨下弹性垫板模型。弹性垫板尺寸为170 mm×150 mm×10 mm。弹性垫板的网孔生成方式如图4所示:网孔参数a1为弹性垫板的上、下表面正六边形内接圆的直径,a2为弹性垫板(图5)的1-1截面正六边形内接圆直径,h为弹性垫板厚度,b为网孔间距,通过网孔间距向周围衍生。该垫板的单元类型为六面实体,单元数为227 560个。

图3 网孔式垫板有限元模型
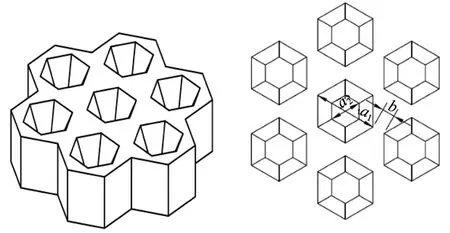
图4 网孔衍生方式

图5 网孔式轨下弹性垫板剖面
为了充分发挥网孔弹性垫板高弹性材料的性能且满足刚度均匀的要求,所有网孔应选用尺寸相同的同心正六边形(俯视),弹性垫板相邻网孔的间距相等,且弹性垫板上、下表面到1-1截面的距离均相等。
由于承载钢板受压变形将导致局部位移不均匀,故将承载钢板与支承钢板设为刚体。模型主要承受垂向荷载,因此,网孔式弹性垫板与承载刚体、支承刚体之间的摩擦可忽略不计,承载刚体下表面和弹性垫板上表面、弹性垫板下表面和支承刚体上表面均采用绑定接触(Tie)。支承刚体下表面边界条件采用对称/反对称/端部固定进行约束(Symmetry/Antisymmetry/Encastre)。
1.2 传统纵向沟槽型弹性垫板结构与模型
为了与网孔式弹性垫板进行对比研究,建立了如图6所示尺寸为170 mm×150 mm×10 mm的传统纵向沟槽型(15槽)弹性垫板结构。其上表面为7个沟槽,下表面为8个沟槽,沟槽间距为19 mm。沟槽型弹性垫板的有限元模型如图7所示,其中模型的接触方式和边界条件均与网孔式弹性垫板模型相同。通过有限元模型的计算,分析沟槽型弹性垫板的力学特性,并与网孔式弹性垫板进行对比。

图6 纵向沟槽型轨下弹性垫板侧视(单位:mm)

图7 纵向沟槽型轨下弹性垫板有限元模型
1.3 静刚度计算与加载方式
网孔式轨下弹性垫板主要承受的是来自于列车和钢轨传递的荷载以及弹条的扣压荷载,根据《轨道交通扣件系统弹性垫板》,采用公式(1)确定网孔弹性垫板静刚度值。

(1)
式中F2——轨下荷载与螺栓拧紧荷载之和;
F1——螺栓拧紧荷载;
D2——轨下荷载与螺栓拧紧荷载共同作用下的短钢轨位移;
D1——螺栓拧紧荷载作用下的短钢轨位移。
根据理论计算[15]并结合城市轨道交通工程实际,计算弹性垫板刚度的理论加载区间为15~55 kN。因此,在有限元模型中,采用压强方式进行加载(图8),压强通过所施加的最大荷载与承载面积的比值确定。

图8 有限元模型加载方式
1.4 橡胶材料本构模型
根据对两种Mooney-Rivlin和Yeoh超弹性本构模型进行研究,得出Mooney-Rivlin超弹性材料本构模型能较好地反映中、小型变形且计算具有较高的精度,因此,选用Mooney-Rivlin本构模型模拟弹性垫板的材料特性,其应变能密度函数为
W=C10(I1-3)+C01(I2-3)
(2)
式中,C10和C01为Rivlin系数;I1和I2分别为第1、第2 Green应变张量。
2 关键几何参数优化
在城市轨道交通工程应用中,网孔式轨下弹性垫板的静刚度一般为35~50 kN/mm。首先选用a1=10 mm,a2=5 mm,b=12 mm,h=10 mm的网孔式弹性垫板作为初始计算模型,然后在弹性垫板材料参数和a1不变的前提下,变动a2的范围为5~8 mm,b的范围为6~12 mm,h的范围为9~12 mm,r的范围为0~3 mm,分析4种关键几何参数对网孔式轨下弹性垫板的力学影响。
2.1 网孔间距的影响
橡胶材料参数不变,当网孔间距在6~12 mm变动时,网孔式弹性垫板的静刚度计算结果如图9所示;当a2=8 mm时,其静刚度和最大应力计算结果如表1所示。
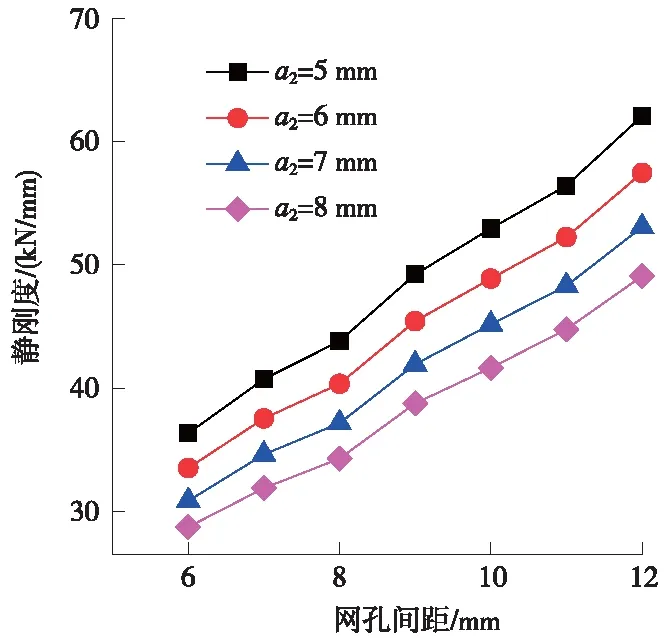
图9 网孔间距的影响
由图9可知,在a2为5,6,7,8 mm这4种工况下,网孔式弹性垫板静刚度的变化趋势基本一致。随着网孔间距的增大,网孔式弹性垫板的静刚度随之近似线性增大。这是因为网孔间距的增大,网孔数量将减少,弹性垫板上、下表面受压面积增大,承受荷载的结构体和垫板承载面积变大,弹性垫板的静刚度将随之增大。

表1 网孔间距对弹性垫板刚度和应力的影响(a2=8 mm)
表1表明随着网孔间距增大1倍,网孔式弹性垫板的静刚度也增大了将近1倍,最大应力值增大了21.97%。因此,网孔间距对网孔式弹性垫板力学影响显著。
2.2 网孔内接圆直径a2的影响
其他参数不变,当a2在5~8 mm变动时,弹性垫板的静刚度计算结果如图10所示;当网孔间距b=9 mm时,弹性垫板的静刚度和最大应力计算结果如表2所示。
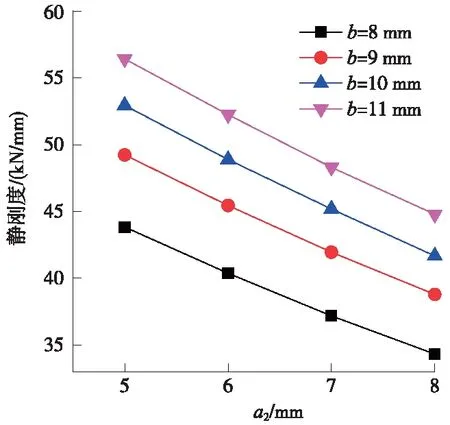
图10 网孔内接圆直径a2的影响
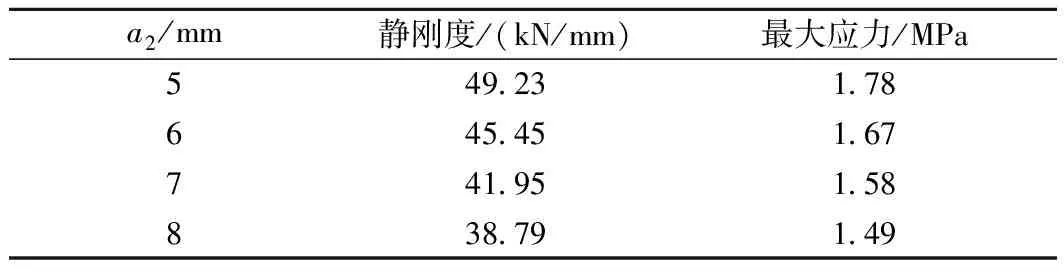
表2 a2对弹性垫板刚度和应力的影响(b=9 mm)
由图10可知,在b为8,9,10,11 mm这4种工况下,网孔式弹性垫板的静刚度变化趋势基本一致。在网孔式弹性垫板的网孔间距不变的前提下,增大a2,弹性垫板的静刚度将近似线性减小。这是因为当a2增大,网孔式弹性垫板体积将小幅减少,弹性垫板的支撑范围有所减少,其静刚度将会减小。表2表明最大应力随着a2的增加而减小,这是因为随着a2的不断增大,网孔单元内壁表面的斜率将逐渐增大,同时弹性垫板主要承受垂向荷载,斜率增大,将使网孔单元内壁表面与垂向荷载之间的夹角减小,弹性垫板的网孔内壁所承受垂向荷载的能力将增大,其最大应力会逐渐减小。根据上述规律,当a2增大3 mm,网孔式轨下弹性垫板静刚度减小了21.21%,最大应力值减小16.29%。因此,网孔内径a2对垫板力学影响较为明显。
网孔间距b和网孔内径a2与弹性垫板的静刚度关系近似线性,与最大应力的关系具有单调性。若调整两者参数,可获得所需静刚度且最大应力较小的网孔式轨下弹性垫板尺寸。因此,相比于传统沟槽型弹性垫板,网孔式轨下弹性垫板具备可灵活调整静刚度和最大应力的优势。
2.3 垫板厚度的影响
选用尺寸为a1=10 mm,a2=8 mm,b=9 mm,h=10 mm的网孔式弹性垫板,取垫板厚度分别为9,10,11,12 mm,分析垫板厚度对网孔式弹性垫板的影响。其静刚度和最大应力值的计算结果如表3所示。
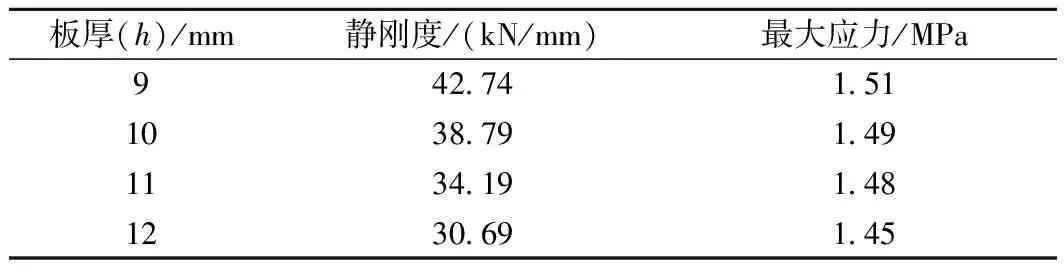
表3 垫板厚度对弹性垫板刚度和应力的影响
表3表明:随着弹性垫板厚度的增加,网孔式弹性垫板的静刚度呈大幅减小的趋势,最大应力值随之却缓慢减小,因此,板厚对网孔式弹性垫板的静刚度影响较大,对其最大应力影响较小。
2.4 倒角半径的影响

图11 垫板受压时的应力集中位置
通过有限元理论计算,发现网孔式弹性垫板最大应力位置主要集中在网孔式弹性垫板中间部分,即1-1截面的正六边形边缘处(图11)。这主要是由于尖角结构的应力集中引起的。为降低尖角附近应力集中,可对网孔式弹性垫板进行倒角处理。倒角部位包括:垫板的上下表面和1-1截面的正六边形内角处、网孔单元内壁垂向尖角处(图12)。倒角半径r分别为1,2,3 mm的网孔式弹性垫板的静刚度和最大应力的计算结果如表4所示。

图12 垫板网孔单元倒角示意
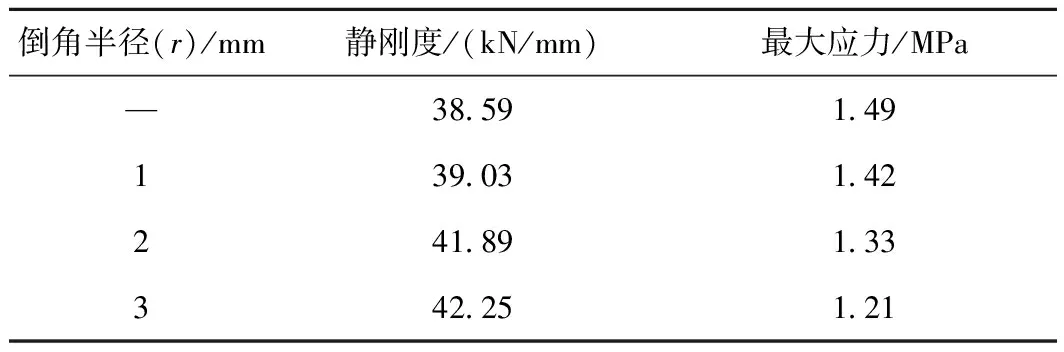
表4 倒角半径对优化垫板刚度和应力的影响
表4表明,倒角后的弹性垫板的静刚度比倒角前稍高,最大应力值减小;随着倒角半径的增加,虽然弹性垫板的静刚度小幅增加,但最大应力值却明显减小。这是因为倒角后的网孔式轨下弹性垫板承载体积和面积小幅增加,弹性垫板的静刚度将随之小幅增加。虽倒角半径为3 mm时弹性垫板的静刚度增大9.5%,但由于将网孔尖角处进行倒角处理,原本应力集中的尖角经倒角处理后变为平滑的圆角,使其最大应力降低18.79%,有效地缓解了局部应力集中。因此,倒角半径对网孔式弹性垫板的受力影响明显。
3 与传统沟槽型弹性垫板对比
从上述不同尺寸的网孔式弹性垫板中选出与纵向沟槽型轨下弹性垫板静刚度相近的弹性垫板,并与沟槽型弹性垫板的受力情况进行对比分析。
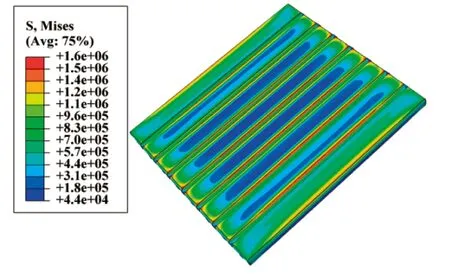
图13 纵向沟槽型弹性垫板应力云图
图13为纵向沟槽型轨下弹性垫板通过有限元计算后的应力云图,最大应力值为1.61 MPa,静刚度为45.65 kN/mm;图14是尺寸为a1=10 mm,a2=8 mm,b=9 mm,h=10 mm,r=3 mm的网孔式弹性垫板的应力云图,最大应力值为1.21 MPa,静刚度值为42.25 kN/mm。从图13、图14可看出,网孔式弹性垫板不仅应力分布更加均匀化,而且其最大应力降低24.84%。若调整网孔式弹性垫板几何参数使其与沟槽型弹性垫板刚度一致时,网孔式弹性垫板所受的最大应力仍明显低于沟槽型弹性垫板,板体应力较小且均匀,将延长其使用寿命。因此,网孔式轨下弹性垫板不仅能在假定刚度范围内灵活调整刚度值,而且可有效地提高弹性垫板的耐久性,将网孔结构应用于轨下弹性垫板具有可行性。
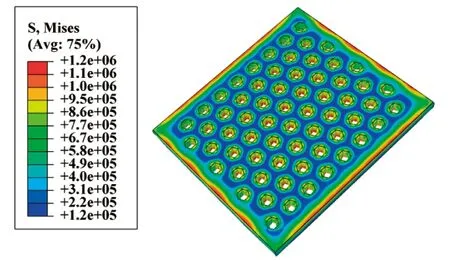
图14 网孔式弹性垫板应力云图
4 结论
通过建立网孔式轨下弹性垫板的三维有限元模型,选用Mooney-Rivlin超弹性本构模型模拟橡胶材料的特性,分析不同网孔间距、网孔内径、弹性垫板厚度、倒角半径这4种关键几何参数对其力学性能的影响,并评估了将网孔结构应用于轨下弹性垫板的可行性,结论如下。
(1)网孔式轨下弹性垫板的静刚度随网孔间距b的增大而近似线性增大,其最大应力值也随之增大;增大网孔内接圆直径a2,弹性垫板的静刚度随之近似线性减小,最大应力也随之减小。增大垫板厚度,其静刚度随板厚的增加而明显减小,但最大应力却随之略微减小。增大倒角半径,虽网孔式弹性垫板静刚度随之略微增大,但最大应力却明显减小。
(2)由于网孔间距b和网孔内径a2对弹性垫板的力学性能影响显著且呈近似线性变化,因此,网孔式轨下弹性垫板的静刚度具有灵活调整的优势。
(3)与传统沟槽型弹性垫板对比结果表明:在网孔式轨下弹性垫板的静刚度稍低于沟槽性弹性垫板的条件下,其最大应力却明显减小25%,可有效提高弹性垫板的耐久性。
(4)网孔式轨下弹性垫板是一种新型弹性垫板,不仅能充分发挥橡胶材料的弹性性能,保持垫板整体应力分布均匀,而且能灵活调整垫板的静刚度并提高其耐久性。将网孔结构应用于轨下弹性垫板具有可行性,为城市轨道交通弹性垫板的研究提供新思路。
