Black Holes and Singularities

Ong Yen Chin

Center for Gravitation and Cosmology, College of Physical Science and Technology, Yangzhou University,Yangzhou, Jiangsu Province, 225002

Abstract: Black holes are arguably the most extreme manifestation of gravity, with horizons that mark the boundary of no return beyond which nothing, not even light, can escape.Recently, remarkable progress has been made on the observational fronts, with the detection of gravitational wave produced by colliding black holes,and “direct” imaging of the supermassive black holes in the galaxy M87.On the theoretical side however,there remains a lot of unsolved mysteries in black hole physics.Of these, the information paradox is the most well-known.Nevertheless,there is another equally puzzling–if not more so–issue,which concerns the very heart of black holes: their singularities, where general relativity breaks down.What happens at the singularities of black holes? Can quantum gravity really remove black hole singularities? Is there a difference between Big Bang singularity and those inside black holes? More crucially, can singularities become naked, i.e.no longer shrouded by black hole horizon and therefore visible to ordinary observers? What is the status of the so-called “cosmic censorship conjecture”? In this review we will go through this topic at a semi-technical level, which is suitable for an ambitious undergraduate students in physics or mathematics.

Key words: black hole; general relativity; singularities; cosmic censorship conjecture

I.BLACK HOLES: HERE BE DRAGONS

On a medieval map, one often finds images of mythical beasts such as sea monsters and dragons in uncharted territories,where potential unknown dangers might lurk.In modern astrophysics,if there is a place that still incites the imagination of the public, it would be black holes.A cosmic prison where nothing can escape from, a portal to another world, or even a library that transcends time and space like the one shown in the movieInterstellar? Science fiction has explored various ideas about what black holes could be.But theoretical physics is a field strange enough that science fiction is pale by comparison, as we will soon see.For now,it suffices to say that black holes are no doubt one of the strangest predictions of Einstein’s general theory of relativity.So strange in fact, that Einstein himself never believed in their existence.In this section, we will first introduce the basic physics of black holes –the parts we understand, before we go down the rabbit hole1In Lewis Carroll’s 1865 classic, Alice’s Adventures in Wonderland,Alice follows a white rabbit who wears a waistcoat deeper and deeper into a bizarre world..We will also explain some subtleties of general relativity and clarify some misunderstandings regarding black holes(unfortunately there are some misleading statements even in professional journal articles)2An advantage of writing a semi-popular science review is that I can take this opportunity to say things that are not so suitable for research journals.For example, how general relativity should be best understood, which of course is highly biased by my personal experience and background..

That said,our story begins a long time ago,before Einstein was born–back in the 18th century.Newtonian mechanics triumphed during this period in history.Powerful techniques of calculus had already uncovered a lot of Nature’s secrets (in fact, calculus was invented exactlyforthe purpose of understanding physical problems; what nowadays students feel like abstract mathematics is deeply rooted in physical problems).But sometimes progress in science requires some imagination inasking the right questions.Some questions seemed almost too easy to ask,but the solutions turned out to be nothing less than profound (the Olbers Paradox is a good example: “why is the night sky dark?”The solution involves an expanding universe which has a beginning in time!) Some other questions sound almost paradoxical, or like an oxymoron, as is the one we will now discuss: “can a star be so massive that we cannot see its shine?”

A.Newtonian Dark Star

If you are observant,and are lucky enough to have a clear view of the starry night sky (a luxury that is hard to come by in many cities nowadays due to light and air pollution), then you would certainly have noticed that not all stars have the same color.The most obvious of all constellations are arguably Scorpius and Orion the hunter.The very heart of Scorpius is a red giant star Antares, its name means “anti-Mars”, as its brilliance in the night sky rivals that of our neighbor planet Mars.Betelgeuse, which marks the armpit of Orion, is another red giant star.These giants are enormous compared to our own Sun.Indeed, large stars tend to burn bright.It would therefore sounds odd to ever wonder about whether a star can be so massive that we cannot see its light.

However, this question is not so odd in retrospect if you recall that in Newtonian physics, there is a simple formula that dictates whether a thrown object can ever escape the gravitational pull of a spherical massive body.This is the escape velocity,whereRis the radius of the body.So the more massive a planet is, the faster one has to throw an object in order for it to escape.Now imagine that light is made of very tiny particle with a very tiny mass trying to escape the surface of a star.It would then be subject to the escape velocity as well.Nowadays we will call particle of light a photon, which is actually massless but has energy, but back in the days these were called “corpuscles”,technically they are not the same idea.The mass of the corpuscle is not very important in the calculation,as it gets canceled from both sides of the equation eventually, which is why at the end the escape velocity does not depend on it.Anyway, we now note that if the massMand the radiusRis such that the escape velocity is equal to the speed of lightc, then it would require a velocity faster than light for the corpuscle to escape the star.Since light cannot escape to observers far away, this would mean that a star like this cannot be seen – it is a “dark star”, a concept first devised by a geologist John Michell in 1783.The famous mathematician Pierre-Simon Laplace proposed the same idea in 1796, independently of Michell.This appeared in the first and second edition of his bookExposition du système du Monde, but was subsequently removed in the later edition, presumably because by then Laplace is a proponent that light is a wave3Nature had more surprise: now we know that light can behave as both particle and wave, but so can electron and other particles.This is the strange world of quantum physics.and therefore has no mass to be affected by gravitational field.

B.General Relativity and the Schwarzschild Black Hole

The black holes as we understand them today had to wait until Albert Einstein formulated his theory of general relativity in 1915.Almost immediately after that (in the same year), the astronomer Karl Schwarzschild, while serving in the German army during World War I,found a nontrivial solution of Einstein Field Equations.These equations are actually ten nonlinear partial differential equations, but in short-hand notation, we write:

The left hand side of this equation aregeometricquantities that describe how space and time are curved by the matter content of the right hand side.In fact,space and time are so intertwined in relativity that we call itspacetime.In older texts, “space-time” is often used,but now we prefer to write it without the hyphen, as it is just one quantity, not a separate thing awkwardly joined together in an ad hoc fashion.Just like Hermann Minkowski– Einstein’s mathematics teacher– wrote in 1908, after he reformulated Einstein’s special relativity geometrically,

“The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength.They are radical.Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows,and only a kind of union of the two will preserve an independent reality.”

The equations are in general notoriously difficult to calculate, but it is possible if one makes some assumptions to restrict the form of the solutions.What Schwarzschild found was a solution that describes a spherically symmetric massive object in Einstein’s theory.Einstein himself was pleasantly surprised that someone could provide a solution in so short a time,not to mention under the battle condition! Unfortunately Schwarzschild passed away just a year later,due the autoimmune disease pemphigus,which he developed while at the Russian front.Nowadays, we write the Schwarzschild solution as

This requires a fair bit of explanation.However,it is actually quite simple to appreciate the expression– it is more or less just the Pythagoras theorem! In two dimensional Euclidean geometry, the Pythagoras theorem is

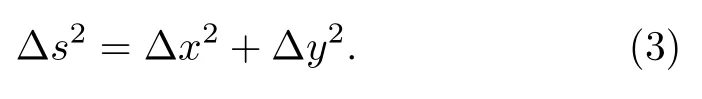
Here the notation ∆s2really means (∆s)2, and similarly for the infinitesimal version (imagining taking an extremely tiny right triangle) ds2really means (ds)2:

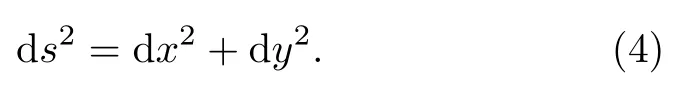
Infinitesimal way of thinking is often used in physics,which is of course not mathematically rigorous.However, our aim here is toappreciateEinstein’s theory, not to teach a course on differential geometry.In three dimensional Euclidean space,it is a matter of high school geometry to show that

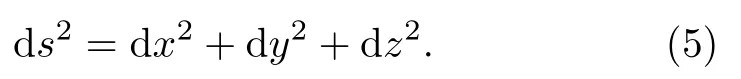
The simplest of all spacetimes is the Minkowski spacetime, described by

In addition to 3 spatial dimensions,there is also a temporal dimension.Note that the temporal term has an opposite sign compared to the spatial part.Although space and time are now combined as a single entity spacetime,time itself is not on an equal footing with the spatial dimensions–we can only move forward in time.The minus sign captures the causality of spacetime.Note thattandx,y,zhave different physical dimension(e.g.measured in second and meter, respectively),so it should really be−c2dt2to make the physical dimension right.However, for brevity of the equations,here we use the usual convention thatc=1.Similarly,we will set Newton’s constantG= 1 in the following discussion.In general, the spacetime Pythagoras theorem can be written as

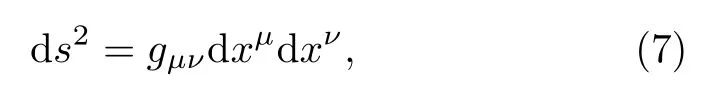
which is a short hand notation that means summing over all the repeated indices.In two dimensional spacetime, where we denotet=x0andt=x1, this means

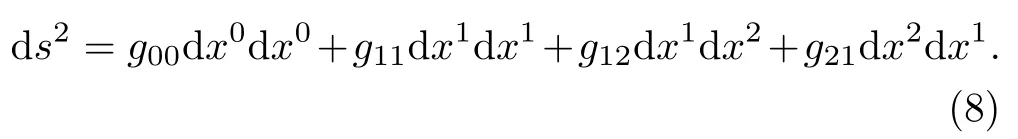
We callgµνthe(components of the)metric tensor.It is symmetric in the indices, i.e.the last two terms above are identical.Thus, the Schwarzschild metric, with the convention thatc=G=1, is just a more complicated geometry of a 4-dimensional spacetime

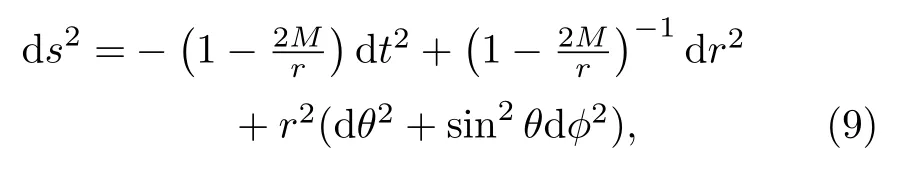
which unlike the Minkowski spacetime,is curved.From the metric tensor, one can construct various geometric quantities that describe this curvature,for example the Riemann curvature tensor,for which one obtains the Ricci tensorRµνand the scalar curvatureR,which appear in the Einstein’s field equations Eq.(1).

In fact, the metric Eq.(1) is not the one presented originally by Schwarzschild.Although the geometry is the same,one could use differentcoordinate systemsfor the convenience of calculations.For example, the flat space geometry in the Cartersian coordinates (x,y),

can also be described in the polar coordinates (r,ϕ):

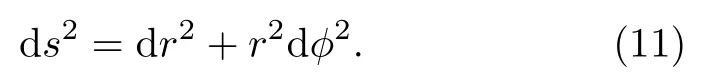
Schwarzschild, influenced by Einstein, chose to work with a coordinate system such thatknown today as the “unimodular gauge”.Furthermore his coordinate system only covers the exterior of a black hole, and therefore it was not immediately obvious that the solution describes something strange.The metric in the form Eq.(9) was found by Droste, and here it is quite obvious that something peculiar happens atr= 2M(this really meansr= 2GM/c2), the Schwarzschild radius.Recall that this is the same expression as the radius of a Michell-Laplace dark star.At this radius, the coefficient of dt2vanishes, while the coefficient of dr2diverges.For a long while people thought that something strange must happen at the Schwarzschild radius,perhaps spacetime ends there and one cannot go below it.However, coordinates can be misleading.The fact that something bad happen when using a coordinate system at a certain spacetime point does not necessarily mean that there is something physically wrong with the spacetime itself.In fact,more often than not,this is just because the coordinate system is not suitable anymore at those points.

Indeed, nothing drastic happens at the Schwarzschild radius, an object can pass right through it.However, it would be a one way trip.The Schwarzschild radius marks the boundary of a black hole, known as the “event horizon”.It is not a physical surface.In fact the Schwarzschild black hole consists entirely of anempty spacetime.It is the nontrial curvature of the geometry that prevents anything from escaping the black hole once it gets below the horizon.One simple way to appreciate this is to note that forr< 2M, the coefficient of dt2term changes sign and becomes positive, whereas that of dr2becomes negative.We have previously agree that the sign (−,+,+,+) in the metric means that we have 3 spatial dimensions and 1 temporal one.After the change of sign upon horizon crossing this is still true, however, the coordinateris no longer a radial direction, but a temporal direction! Similarlytis now a radial direction.Since any object can only move forward in time–in the future direction,ithas tomove in the direction marked by decreasingr.This is the fundamental reason why nothing can escape a black hole, to do so would amount to traveling backward in time.

Note thatr= 0 is also problematic, as the term 2M/rdiverges so the metric breaks down.This time however,it is a true singularity,and cannot be removed by changing coordinate systems.In general relativity,it is good to work with “scalar quantities” obtained by contraction of various tensors since they are unchanged under coordinate transformations.For example, the Kretschmann scalar is defined by the contraction of the Riemann curvature tensor:K=RλµνρRλµνρ.In the Schwarzschild spacetime,Kis only a function of the radial coordinater.Specifically,

Note that atr= 2M,Kis finite, so there is nothing strange with the curvature at the horizon.On the other hand, atr= 0,Kdiverges, which means that it is a true singularity.

It is common to read in the literature that“r=0”is the center of the black hole, or the “central singularity”.This is at best misleading – there is nothing“central” about a singularity situatedin time.The Schwarzschild singularity is not a point in space, but an event in the future, all objects falling into the black hole eventually hits it in finite proper time measured by their own clock.As far as we understand, spacetime ends at the singularity, which itself is “infinitely curved”.A common misunderstanding is that an observer who falls into a black hole would see the singularity in front,situated at the center.Resisting with all his might,the observer finds that he is completely helpless,the gravitational pull is too strong and so he could only watch his inevitable plunge towards the singularity.This isnotthe correct picture.What happens is far stranger–the observer cannot see the singularity,since it is an event in the future that has not happen yet.He still cannot avoid hitting the singularity,but for a completely different reason:r= 0 cannot be avoided just like we cannot avoid the next Monday from arriving.The future is inevitable.

C.The Kerr-Newman Family and the Reissner-Nordstrm Black Hole

It turns out that black holes in general relativity is rather simple, in the sense that there are only three parameters that completely characterize a black hole:the massM,the chargeQ,and the angular momentumJ.Suppose a black hole is neutral and not rotating,then it is completely characterized by mass.Suppose a star collapses into a black hole of massM.If we could take a lot of chocolate and let them collapse into a black hole of the same mass, then these two black holes are completely the same.The black hole forgets its past,it does not care about what constituents were there before the black hole formation.Similarly, if you drop a cup of coffee into a black hole, its mass would increase by a tiny bit.But nothing else about the coffee can be recovered from the black hole.This eventually leads to the information paradox of black hole.Ultimately,black hole evaporates away due to Hawking radiation,what then happens to the information of the stuff that it contains? In fact, the situation is worse: as we have discussed,stuff falls into the singularity in finite proper time, so how does black hole interior store any information? In any case, quantum mechanics tells us that information should be conserved (in technical jargon,this is because of unitarity of quantum mechanics),but exactly how this is achieved by black holes is an unsolved mystery.This is beyond the scope of the current article.

For our purpose, we would like to emphasize that despite the formidable mathematics, black holes are in fact quite simple.So there are precisely 4 types of black holes in general relativity: the Schwarzschild black holethe Reissner-Nordstrm black holethe Kerr black holeand the Kerr-Newman black holeThey are all part of the Kerr-Newman family.The metric of Kerr and Kerr-Newman black holes are considerably more complicated,so we will not discuss them in much details.

The metric of Reissner-Nordstroblack hole is given by

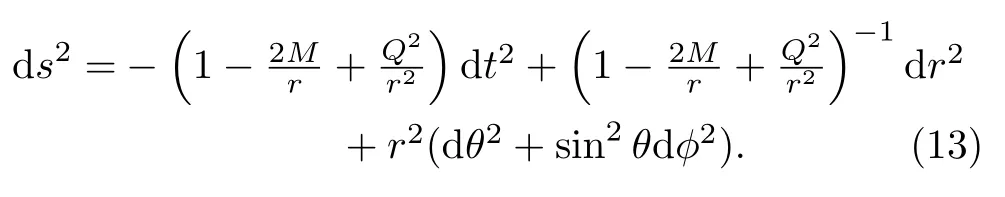
The only difference between this and the Schwarzschild metric is that there is now an additional charge termQ2/r2.Here we use the units in which the vacuum permittivity satisfies 4πϵ0= 1.However, this term makes quite a big change in the structure of spacetime.The horizon of the black hole is now located at the root of

This is a quadratic equation inr, so it is easily solved:

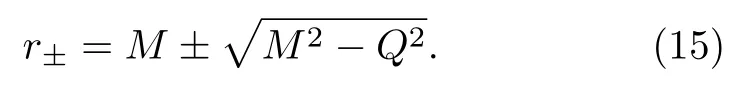
Note that ifQ= 0, we recover the Schwarzschild radius atr=2M.What Eq.(15)is telling us is that there are two horizons in the Reissner-Nordstrm spacetime.The larger rootr+is the event horizon, which like the Schwarzschild case, marks the boundary of no return.The smaller rootr−corresponds to an inner horizon,which will play an important role in our discussion below in the context of cosmic censorship conjecture.

Note that the sign of the coefficients of dt2and dr2change twice asrdecreases.First, a sign change occur at the event horizon.This implies that the observer has to continue to travel in the decreasingrdirection (which is a temporal direction), until it passes through the inner horizon, when the sign changes yet again.So inside the inner horizonrdenotes radial direction, just like outside the black hole.The inclusion of a single electron in spacetime therefore changes the property of spacetime rather drastically.In particular, the singularity is now a location in space, instead of an event in time.In physics jargon, we say that the Reissner-Nordstrm singularity is timelike,whereas the Schwarzschild singularity is spacelike.The Reissner-Nordstrm singularity is therefore visible to the observer inside the inner horizon, but they are not helplessly attracted by it.In fact, not much effort is required to avoid hitting the singularity, the gravitational field in the vicinity of the singularity turns out to berepulsive.This repulsion is not due to the electric field, but a gravitational one that affects all objects, even neutral objects.To appreciate why this is so, we first need to understand how the metric can give information about the gravitational field.In the Newtonian approximation,the gravitational potential is related to the metric coefficient by:

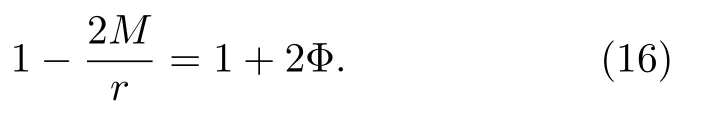
That is, Φ =−M/r, which gives the Newtonian forceF=−∇Φ =−M/r2.In the Reissner-Nordstrm case,we would have instead,

so that Φ =−M/r+Q2/2r2.Thus the potential is zero at

Near the vicinity of the singularity below this value ofr, gravity becomes repulsive.In fact, although the mass of the entire black hole is positive,the mass of the singularity is negative (to be more precise, the quasilocal energy near the singularity is negative.)

In fact, it is interesting to compare the negative mass singularity of Reissner-Nordstrm black hole with the Schwarzschild solution in which the mass is negative:

We note that the Reissner-Nordstrm black hole can be obtained from the Schwarzschild’s solution by replacing the Schwarzschild’sMby the effective massMeff=M −Q2/(2r).The repulsive gravity in the regionr

Now that we have seen some examples of naked singularities, let us discuss it formally.

II.NAKED SINGULARITY AND WHY DO WE CARE

A naked singularity simply means that the singularity is not shrouded behind a horizon and becomes visible to outside observers.Roger Penrose proposed that naked singularities should not be allowed in general relativity.This proposal is called the “cosmic censorship conjecture” – naked singularities are bad and its existence should be “censored”, at the very least it should be covered by the horizon of a black hole.Before we can appreciate why Penrose proposed such a censorship, we must first discuss what singularities are and why they are considered to be bad.

There are at least two ways to understand singularities.One of which is simply that there are points or regions in spacetimes such that an observer terminates at.An observer who falls into a Schwarzschild black hole, for example, will be doomed to hit the singularity (which as we explained, lies in the future) in finite proper time, which is at mostπM.Technically, we include trajectories of massless particles such as light as well.So intuitively we can think of singularities as points where observers(including light)abruptly come to an end.Another definition for singularities are more physical – it is where suitably constructed curvature quantities blow up.Note that these two definitions are not equivalent.We could, for example, artificially remove a point in Minkowski spacetime so that there are trajectories that terminate on it.However,such an example is rather contrived, and mathematically it is easy to “patch up” the point to remove the singularities.Indeed, in general relativity gravitation is curvature of spacetime.Therefore the definition that singularities are where curvature is infinite makes more physical sense.The problem is that the theory of general relativity cannot work with infinite curvature.We say that the theory breaks down at the singularities.To make sense of singularities we would need a working theory of quantum gravity,i.e.to go beyond general relativity.

It is often said that in quantum gravity, singularities will be smeared out and so there will no longer be any problem.However, we cannot be sure about this,since after all we do not have such a theory.Hawking’s view in [1]is that if the singularity is indeed smeared out by quantum correction, things would be rather “boring” since gravity would then be “just like any other field”, whereas gravity should be distinctively different since it is not just a player on a spacetime background, it is both a player and the evolving stage.Indeed, notwithstanding the quantum field theory description of gravity as being mediated by a particle called graviton, gravity does seem to be rather unlike other fundamental forces.As Buchdahl put it[2],

“Field? ― We have no field in the sense in which one has a Maxwell field.Whenever I have used the term ‘field’ [in the context of the metric]I have done so as a matter of mere verbal convenience.[...]The classical fields – the electrostatic field, for example – in the first instance had, so to speak, a subjunctive existence.LetPbe a particle satisfying all the criteria of being free except in as far as it carries an electric charge.Then ifPwere placed at some point it would be subject to a force depending on the value of the field intensity there.In particular, when the latter is zero there is no force.[...]the “true” fields subjunctively quantify the extent to which a given particlePis not free, granted thatPwould be free if any charges it may carry were neutralized [...]this field [the metric], unlike the ‘true’ fields, cannot be absent, cannot be zero”.

Since we cannot guarantee that singularities can be resolved in quantum gravity,it stands to reason that it is best if we can deal with issues caused by their presence already in general relativity, or at least semi-classical gravity incorportaing some quantum effects that we do understand.

But what is so bad about singularities? Part of doing physics is to be able to predict the future, in the sense that given a physical system at some initial time,sayt=0, we can solve the equations to evolve the system in time, tofullydetermine what happens to the system at a later time, sayt= 1.The problem with a naked singularity is not so much about what happens there or even in its vicinity, but their influence on other part of spacetimes.Naked singularity, by definition,means that it is visible to outside observers.So whatever happens to the observer is not completely determined by initial conditions given at some past instances, but also whatever comes from the singularity.Technically this means that we must also impose a boundary condition on the singularity.Since we know nothing about singularities, this we cannot do.The existence of naked singularities therefore means that future is no longer fully determined; there is a loss of predictability in general relativity.On the other hand, if naked singularities exist in the actual Universe, presumably we can learn a lot about quantum gravity by observing its signals,so from that perspective,naked singularities are opportunities, not to be feared.

According to our best model of the cosmos,the U-niverse itself begins at a Big Bang singularity.One often reads that the Universe begins with a point.However these two statements are not quite equivalent.If the spatial extend of the Universe is indeed infinite, then it must also be infinite already at the Big Bang.Singularities need not be pointlike.In any case, the Big Bang singularity is in our past.It does not give rise to any problem since one can fix initial condition at some later timeafterthe initial singular moment, and let that evolves forward under Einstein’s equations.Whether there was a singularity before that is not crucial to describe the future events.Likewise, the Schwarzschild singularity, which is in the futureat the end of timeis not problematic as far as initial value problem is concerned; there simply is no spacetime anymore beyond it to evolve to.Both of these singularities are moments in time, in techinical jargon they are spacelike singularities.The problematic ones are naked singularities that one can see, the timelike singularities.Incidentally, since we mentioned the initial Big Bang singularity,we should also mention another conjecture of Penrose.The fact that entropy is non-decreasing function of time means that at the beginning, the entropy is incredibly small.So in some sense the Big Bang singularity has very small gravitational entropy.The difficulty lies in the fact that we do not quite understand how to properly define gravitational entropy.Penrose proposed that one should consider the Weyl curvature,a quantity that describes tidal distortion due to gravity.Low gravitational entropy would mean that Weyl curvature is zero(or close to zero).On the other hand, under gravitational collapse one expects that black hole singularities would be rather “messy”, i.e.highly distorted by tidal effect.So they would have large Weyl curvature.Not all singularities are equal.

III.COSMIC CENSORSHIP CONJECTURE

To summarize, the initial and final singularities in time are not problematic, the naked singularities are.So Penrose proposed that there cannot be naked singularities in general relativity.There are two versions of the cosmic censorship conjecture.Theweak cosmic censorship conjecturesimply states that there should not be a naked singularity outside a black hole horizon.The Reissner-Nordstrm singularity, while naked to an observer in its vicinity, does not affect the outside world(since no signal can escape a black hole horizon).Therefore these singularities are not so problematicas far as the black hole exterior is concerned.Thestrong cosmic censorship, on the other hand, requires that there should not be any naked singularity, even inside a black hole.More technically, it requires that spacetime be globally hyperbolic, i.e.initial condition can fully determine the future of the whole of spacetime, including the black hole interior.After all, at least in principle, one can consider going inside a black hole to do physics.Therefore, it makes sense to want the black hole interior to be free of pathologies as well.

Initially the hope was that no naked singularity can ever be formed.However this has been proven false,and there are now a plethora of examples in which naked singularities do form,including under gravitational collapse.So the conjecture is now refined so that it states that naked singularities arenot generic.This means that given an initial condition that leads to a naked singularity, if we choose a nearby initial data (i.e.perturb it a little bit),the evolution should no longer result in a naked singularity.That is to say, the conditions that could lead to naked singularities are in a sense,fine-tuned.

The current status of the cosmic censorship conjecture is not so clear.It is fair to say that at this stage we are still gathering data about exactly when the censorship is violated.For example, it was already known for some time that in higher dimensions, there can be“black strings”, which is unstable (Gregory-Laflamme instability) and will eventually pitch off at multiple points along the extra dimension.The point of breaking becomes a naked singularity.Recently, it was also found that black hole collisions in higher dimensions can produce naked singularities, since energy loss via gravitational wave becomes smaller as the number of spacetime dimension increases.On the other hand, the most well-known attempt to produce naked singularities is probably the attempt at over-spin or over-charge a black hole.

Recall that a Reissner-Nordstrm black hole has two horizons:For any fixed massM, there is a maximalQ, namelyQ=M, for which the square root is well-defined in the real numbers.In fact, note that forQ=M, the two horizons coincide.This is known as an extremal black hole.Similar configuration can also happen in the case of rotating black holes.So if one can throw in a charged particle into an extremal black hole such that the end state satisfiesQ>M, then there would no longer be any horizon,and the singularity becomes naked.However, it is not easy to throw such a particle inside, due to a potential developed around the black hole.Analysis of such a process is also rather difficult since one should properly take nonlinear effect and backreaction into account.

The inner horizon has a different story.If the strong cosmic censorship conjecture is correct, one has to deal with the singularity inside the inner horizon.This is accomplished by the instability of the inner horizon.The inner horizon has the property that incoming light and other waves get blue-shifted into higher and higher energy, which eventually destroy the inner horizon.This changes the structure of the spacetime,and the singularity becomes a spacelike one much like the Schwarzschild singularity.If this indeed happens,predictability is recovered.However, there is evidence that in some other black hole spacetimes,the blue-shift instability need not occur and so the strong cosmic censorship is violated in the strict sense[3].Nevertheless,it does not seem that solutions can be extended pass the inner horizon,i.e.the evolution via Einstein’s equation stops at the inner horizon[4].In this sense the spirit of the strong cosmic censorship is still preserved.It remains to further understand what happens physically when an object hits the inner horizon.

IV.CONCLUSION

Despite progresses over the past century trying to understand general relativity,and observational success of black holes recently via gravitational wave detection and “direct” imaging of the supermassive black hole in M87, our understanding of the singularities are still in its infancy.For a long time we thought the Universe is safe from naked singularity.However, our universe is best modeled by the so-called de-Sitter spacetime.This is a spacetime in which there is a positive cosmological constant that accounts for the accelerating expansion of the Universe.However, it was exactly in de Sitter spacetime that charged black holes could violate strong cosmic censorship[3].Granted that highly charged black holes are unlikely to exist in the Universe since charge tends to get neutralize fairly quickly by absorbing opposite charges from the environment, this is still disconcerting.

Since singularities are common place in general relativity, and now evidence exists that cosmic censorship can be violated under various conditions, it is of paramount importance that we investigate the nature and effects of such violations.The attitude that singularities will be cured by quantum gravity is more or less brushing our ignorance under the carpet.It is now the right time to face the issue.

ACKNOWLEDGMENTS

YCO thanks the National Natural Science Foundation of China(grant No.11705162)and the Natural Science Foundation of Jiangsu Province(No.BK20170479)for funding support.