铅球出手最佳角度计算与数值模拟

（上海市进才中学，上海 200135）

0.引言

影响铅球运动成绩的好坏不仅受于运动员自身力量、身高、体重等身体条件的限制，还与其背后的物理学原理和客观影响因素有关。

目前对于抛体运动的相关研究已有多篇文献论及，高彩云对抛射体的运动轨迹进行了理论分析和Matlab数值模拟[1]。郑智健对空气阻力作用下的抛体运动方程进行了研究[2]，研究结果表明，在抛射体质量较轻时，空气阻力对抛射体运动轨迹的影响是不可忽略的。苏安对抛体运动与单摆运动进行了Matlab数值模拟[3]，通过建立上述两类运动的基本方程，借助Matlab这一数值模拟软件，将抛体运动与单摆运动的动态过程展现出来，生动而直观。李雨青对抛体运动中抛射角度与抛射距离之间的关系进行了实验研究[4]，得到了不同抛射角度下抛体运动的抛射距离。刘尚昊对斜抛运动抛射角度与距离之间的关系进行了理论探究[5]。沈卫对抛体运动的分解方法进行了研究[6]，在传统正交分解方法的基础上，研究了斜交分解方法，为斜抛运动的分析提供了新的技巧。

1.铅球运动的轨迹方程

1.1 铅球运动的基本方程

对于斜抛运动而言，物体只受竖直方向下的重力作用，可得物体在空中运动的水平位移和竖直位移如下：

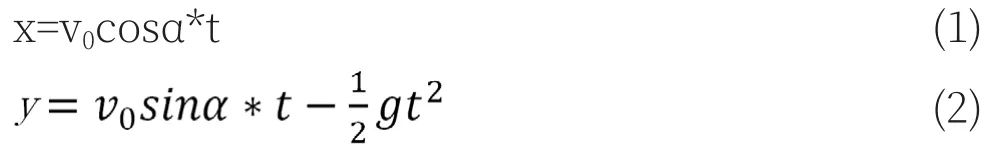
对于抛出点位于地面上的物体而言，其最大射程可以表示为物体水平方向的分速度与运动时间的乘积，令式(2)中y=0，可得斜抛运动落地时间表示如下：

根据式(3)可得，对于抛出点位于地面上的物体而言，其落地点与抛出点之间的距离(射程)关系可以表示为：

可见，对于抛出点位于地面上的物体而言，其射程与初速度的平方成正比，同时与物体抛出时初速度方向有关。当α=45°时，式(4)取得最大值，即当抛出角为45°时，可获得最大射程：

然而，对于铅球运动而言，其抛出点具有一定的高度(通常位于运动员头部位置)，因此上式最大射程不能直接用于铅球落地距离的计算，对于铅球运动需要建立新的运动学模型。

本文将铅球运动简化为离地具有一定高度的斜抛运动，如图1所示。图中h为铅球抛出点高度，v0为铅球抛出时的初速度，α为铅球抛出时初速度方向与水平方向的夹角。

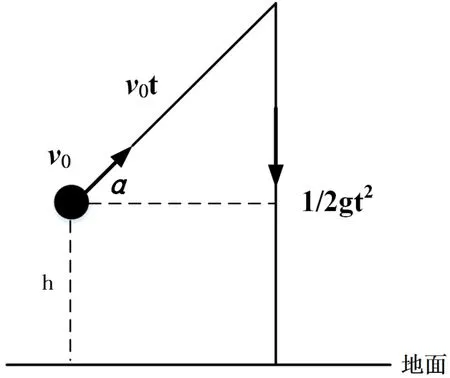
图1 铅球运动建模示意图

由图1可知，铅球在水平方向上匀速直线运动位移与竖直方向上的自由落体位移可表示如下：

以竖直向上为正方向，当铅球落地时，其竖直方向上的位移为-h。因而由式(8)可得铅球在空中的运动时间。

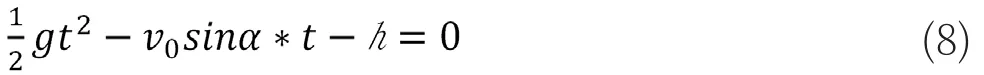
解上述二次方程并略去t＜0的解，可得铅球落地时间：

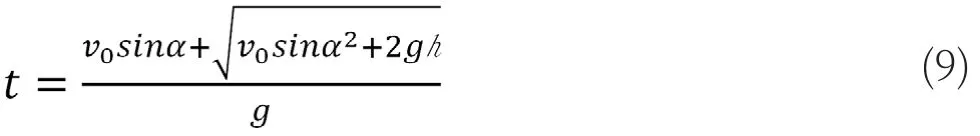
由于铅球在水平方向上做匀速直线运动，将式(9)代入式(6)可得铅球落地点与其抛出点之间的水平距离(射程)为：

由式(10)可知，铅球的射程与其抛出时的初速度的大小和方向以及抛出点距地面的高度有关。然而，相较式(4)抛出点位于地面上的物体射程函数而言，对式(10)函数求取最大值(即铅球的最大射程)是一项比较复杂的工作。

1.2 铅球最大射程求取

通常，对抛体运动的分解方法主要是将抛体运动分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动，由此可得式(10)射程函数。然而，对式(10)函数难以求取最大值。因而本文采用独特的分解方法，即建立图1所示的“斜坐标系”。本文通过转换坐标系的方法，可以很方便的求解铅球的最大射程，从而避免对式(10)复杂函数求最大值的难点。

在图1由抛体竖直位移，射程以及沿初速度方向的位移为边所构成的三角形中，利用勾股定理可以得到水平位移，即铅球在抛射角为α时的射程。

整理可得，铅球射程的平方是关于其落地时间的函数，在对此函数进行换元，令t2=t，函数变为二次方程，如下式所示：

由式(12)可方便的求出铅球射程取得最大值时铅球的运动时间，即铅球运动时间满足下式时，可获得最大射程：

此时，铅球竖直方向的位移y=1/2gt2。由图1中的三角形关系可得，当铅球获得最大射程时抛射角满足：

1.3 空气阻力的一般规律

具有一定体积的物体在空气中运动时，由于要排开前方空气，因而不可避免的受到空气阻力的影响，且该阻力与运动物体的形状、体积、表面光滑程度以及物体的运动速度均相关。根据斯托克斯定律可知，半径为R的球体在空气中所受的粘滞阻力为：

由式(15)可知，当铅球抛出后其沿运动方向的阻力与其运动速度成正比，从而在空气阻力的作用下，铅球向前的水平速度将被削弱，使其运动轨迹偏离理想状态下不受空气阻力的抛物线，呈现一条“弹道”轨迹。

1.4 空气阻力作用下铅球的运动方程

如式(14)所示，以铅球抛出点为原点建立直角坐标系，把式(15)的空气阻力分别分解在水平方向和竖直方向上，如图2所示。

图2 铅球所受空气阻力示意图

根据牛顿第二定律F=ma=mΔv/Δt，即速度变化量除以时间变化量Δv/Δt与质量m的乘积等于物体所受的合外力，因而可分别在水平和竖直两个方向上列写牛顿第二定律方程，构成如下方程组：

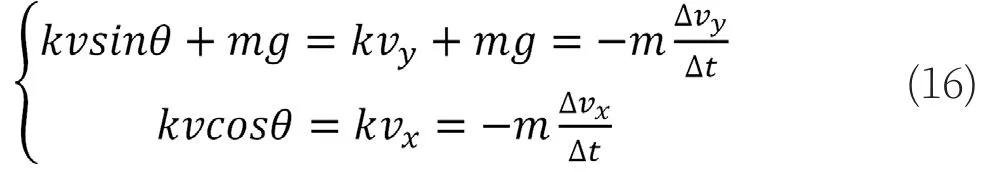
其中，vx、vy分别为铅球速度在水平和竖直两个方向上的分量，θ为铅球速度与水平方向的夹角，k为空气阻力的比例系数。随着铅球的运动，铅球速度的大小，方向都是变化的，因而当受到空气阻力时，铅球在空气中做变加速曲线运动，即上式铅球速度的两个分量均为时间的函数。

通过查阅文献资料，形如式(15)的方程描述了物体速度变化率与力之间的关系，称为微分方程，由于方程中各项系数，如比例系数k以及铅球的质量均为常数，因此上述微分方程为常系数微分方程，可直接利用常系数微分方程公式进行求解，从而得出铅球两个分速度随时间的变化关系，如式(17)所示：

其中，vx、vy分别为铅球速度在水平和竖直两个方向上的分量，θ为铅球抛出时的初速度与水平方向的夹角，k为空气阻力的比例系数。

由式(17)可知，当铅球受到空气阻力作用时，其水平速度与时间呈负指数规律衰减，从而使铅球水平速度逐渐减小，若铅球在空中运动的时间足够长，其水平速度将衰减为0，而仅剩下竖直方向速度做落体运动。

2.计算机数值分析

2.1 运动参数与初始条件

设运动员出手时铅球的速度通常在30km/h左右，且此初速度越大铅球的射程越远。本文在Matlab软件中设置铅球抛出速度为10m/s，取重力加速度为9.8m/s2，认为铅球运动员掷铅球时的出手高度为1.75m

2.2 铅球最佳出手角度理论验证

将2.1节所设置的铅球初始运动参数输入Matlab中，利用Matlab软件对0°～180°范围内的抛掷角度进行射程计算，从而绘制“出手角度—射程”曲线如图3所示，并在图中标出极值点的位置如下。

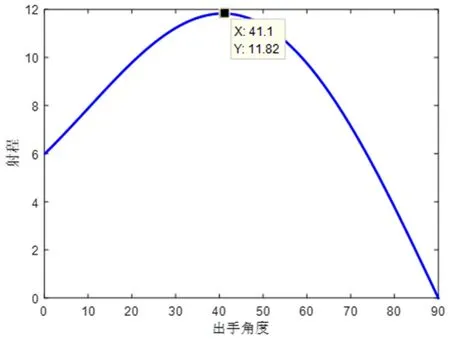
图3 铅球“出手角度—射程”曲线

由图3可见，在铅球初速度为10m/s，出手高度为1.75m时，随着铅球出手角度的增大，其射程先增大后减小，存在极值。当出手角度为41°左右时，铅球可获得最大抛射距离。当出手角度增大为90°左右时，其射程降为0，即此时相当于竖直上抛，无水平位移。对比式(13)理论计算结果，可见竖直仿真与理论计算高度吻合，从而验证了本文理论计算的合理性。

3.结论

铅球作为一种广受民众喜爱的田径运动，其背后还隐藏着非常丰富的物理学原理。本文应用抛体运动基本知识，对铅球出手角度与落地距离之间的函数关系进行了研究，在此基础上推导了最佳出手角度。理论计算结果表明，铅球投掷距离还与其出手角度有关，在铅球出手初速度以及出手高度一定的条件下，铅球射程与出手角度曲线存在某一极值，运动员可通控制铅球出手角度(通常为41°～43°)以获得最佳比赛成绩。