Al元素含量对高熵合金AlxFeTiCrZnCu力学性能的影响

王兰馨， 温 斌， 姚 山

(1. 运城学院， 运城 044000; 2. 燕山大学， 秦皇岛 066004; 3. 大连理工大学， 大连 116024)

1 引 言

多主元高熵合金的概念是上世纪90年代提出的，是在传统多主元合金设计思想的基础上对传统合金发展框架的突破而形成的一种新的合金发展理念[1-5]. 研究表明，高熵合金体系体现出多种金属元素集体效应而表现其高熵特色，原子排列混乱，但是又呈现出简单的结晶相[3,4]. 高熵不但有助于合金微结构的简化，而且会使微结构倾向于纳米化及非晶化[2-5]. 高熵效应会促进元素间的混合，形成简单的体心立方结构或是面心立方结构，从而抑制脆性金属间化合物的形成. 由于多主元高熵合金的特性是多个主要金属元素的共同体现，因此高熵合金具有很多传统合金所不具有的优异性能[6-8]，如高硬度、高强度、耐热性，耐腐蚀性等等，因此具有较高的学术研究价值和较大的应用发展空间. 但是目前国内外对高熵合金的研究大都集中在实验上，例如从高熵合金这一概念提出到2004年才用真空熔炼法合成的高熵合金AlCoCrCuFeNi[8]，主要研究了其热喷涂涂层的氧化性能并对其耐磨性进行了改良[3]，以及研究了AlxCoCrCuFeNi的微观结构特征[9]、机械性能[10]、粘着磨损特性[11]、元素含量对其的作用[12]等等. 直到2008年印度科学家通过机械合金化方法制得了AlFeTiCrZnCu高熵合金[13]，并研究了该种高熵合金的热固结性能和机械性能[14]. 研究结果表明，AlFeTiCrZnCu高熵合金具有简单的立方晶体结构，所含金属元素之间并未形成较复杂的金属间化合物；而且AlFeTiCrZnCu合金系具有较好的性能，即使在800 ℃下烧结一小时后也具有较高的硬度.

通过已有研究表明高熵合金的合成过程比较复杂，特别是稍微改变组元含量后的合成更难控制，因此对其物理化学特性的理论研究结果也非常有限. 第一性原理计算方法不需要任何参数，只需要一些基本的物理常量就可以得到体系基态的基本性质. 其中的密度泛函理论是一种研究多电子体系电子结构的量子力学方法，在研究分子和凝聚态的性质中应用非常广泛. 如第一性原理计算Al-Ni系金属间化合物的性质[15]，Ni-Ta系金属间化合物的性质[16]等等. 因此，本文采用第一性原理密度泛函理论和平面波赝势的方法计算AlxFeTiCrZnCu高熵合金的结构性能、弹性性能、生成热等. 其中x表示Al元素的摩尔含量，分别为0，0. 5，1，1. 5，2，3，其余金属元素的摩尔含量均为1.

2 计算方法

本文的第一性原理密度泛函理论的计算采用基于平面波赝势方法的Materials Studio软件中的CASTEP模块[17]，固溶体结构模型采用虚拟晶体近似(VCA)[18-20]的方法建立. 由于高熵合金AlxFeTiCrZnCu具有不完全有序的体心立方结构[13]，为了避免在使用VCA方法建模过程中产生所谓的“虚拟原子”[19]或长程结构中所累积的误差[20]，本文在单个晶胞中的单个原子上采用VCA方法建立晶体结构. 表1中列出了Al元素的摩尔含量、百分含量及其它元素的百分含量. 以体心立方BCC结构中Al元素摩尔含量为0.5时的高熵合金为例，Al元素的质量分数为9%，其它元素的含量均为18.2%，如图1所示，在单个晶胞中的每个原子上采用VCA方法建立高熵合金的晶体模型. 这种建模方法避免了超胞模型所带来的计算过程的复杂和时间过长. 计算过程中，电子间的交换-关联函数采用广义梯度近似(General gradient approximation, GGA)[21]下的PBE泛函[22]，采用基于第一性原理的模守恒赝势(Norm-conserving Pseudopotential, NCP)[23]来处理电子-离子的相互作用，计算平面波函数展开的动能截断取为700 eV，倒空间中k点网格间距行为0.4 nm-1，剖分网格为10×10×10.

在以上参数设置的计算条件下，对计算结构的准确性进行了验证. 通过验证计算，体心立方BCC结构的Fe晶体的晶格常数为0.284 nm，与实验值0.287 nm[24]接近，由此可见，本文所选取的计算参数较为合理.

表1 Al元素的摩尔含量、百分含量及其它元素百分含量

Table 1 Mole content and mass fraction ofAl, and mass fraction of other elements

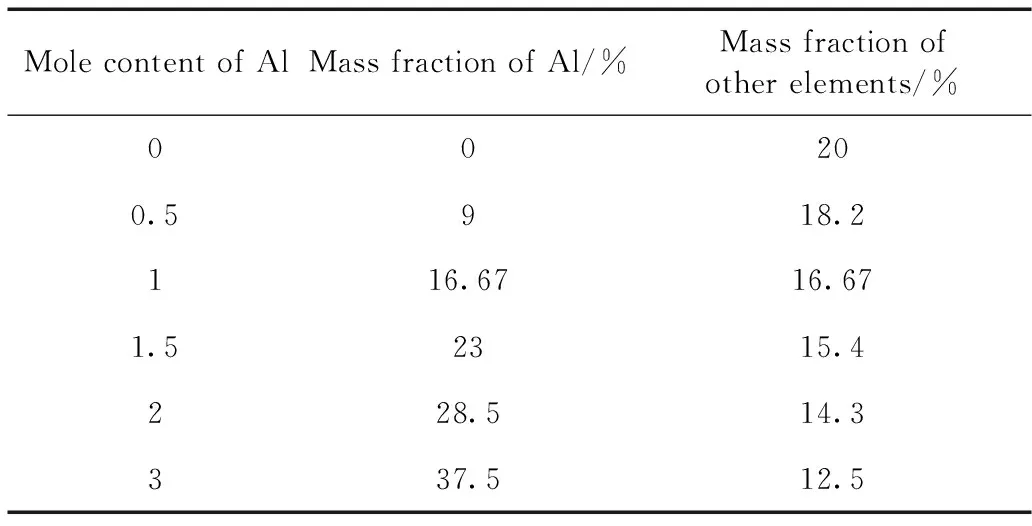
Mole content of AlMass fraction of Al/%Mass fraction ofother elements/%00200.5918.2116.6716.671.52315.4228.514.3337.512.5

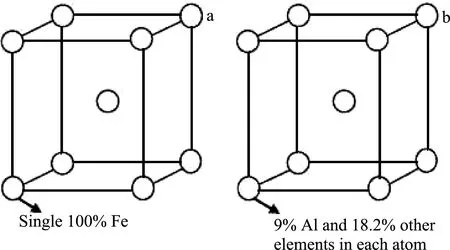
图1 采用VCA方法建立高熵合金结构模型Fig.1 The model of high entropy alloy built by VCA

3 结果与讨论

3.1 结构性质

在以上设置的计算参数下，本文对高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2, 3)的晶格结构进行了优化，优化后的高熵合金晶格常数和密度列于表2中. 为了直观起见，在图2中画出了晶格常数和密度与Al元素含量的关系. 从表2和图2中可以看出，高熵合金AlxFeTiCrZnCu的密度随着Al元素含量的增大而减小，但是晶格常数随着Al元素含量的增加先减小后增大，在Al元素摩尔含量为1时高熵合金AlxFeTiCrZnCu的晶格常数最小，为2.81 Å. 可以看出高熵合金AlxFeTiCrZnCu在晶格常数最小时并不是密度最大值，这可能是由于Al元素在该高熵合金中的密度最小，因此Al含量的增大反而使高熵合金的密度减小；但是Al元素本身是面心立方FCC结构，因此含量的改变可能会影响高熵合金的晶格常数.

表2 高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2, 3)的晶格常数和密度

Table 2 Lattice parameters and mass densities of the high entropy alloys AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2, 3)

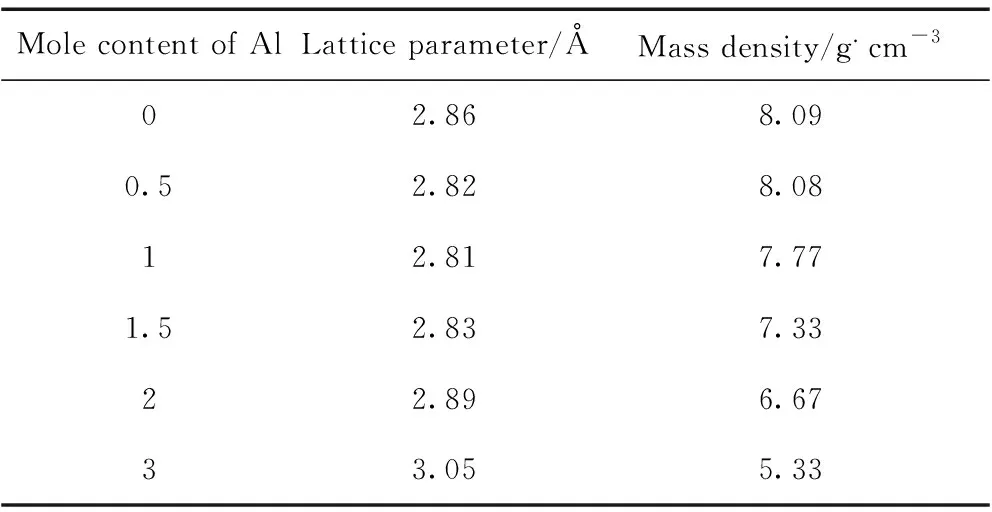
Mole content of AlLattice parameter/ÅMass density/g.cm-302.868.090.52.828.0812.817.771.52.837.3322.896.6733.055.33

图2 高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2, 3)在Al元素摩尔含量不同时的晶格常数和密度Fig. 2 Comparisons of the lattice parameters and mass densities among the high entropy alloys AlxFeTiCrZnCu with different mole content of Al

3.2 弹性性质

在优化了高熵合金AlxFeTiCrZnCu的晶格结构之后，仍采用第一性原理密度泛函理论计算了高熵合金的弹性常数Cij、杨氏模量E、体积弹性模量K及泊松比ν. 表3中列出了不同Al元素含量的AlxFeTiCrZnCu高熵合金的弹性常数Cij，由于高熵合金的简单立方晶体结构，因此弹性常数只有C11、C12及C44. 弹性常数决定了金属材料的力学稳定性，根据力学稳定性判据[25]：

C1>0,C44>0,C11-C12>0,C11+2C12>0

(1)

高熵合金AlxFeTiCrZnCu只在Al元素摩尔含量为2时才符合力学稳定性判据，说明在AlxFeTiCrZnCu高熵合金中适当增加Al元素含量可以提高其力学稳定性.

表3 高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)的弹性常数

Table 3 Elastic constants (Cij) of the high entropy alloys AlxFeTiCrZnCu (x=0, 0.5, 1, 1.5, 2) (GPa)

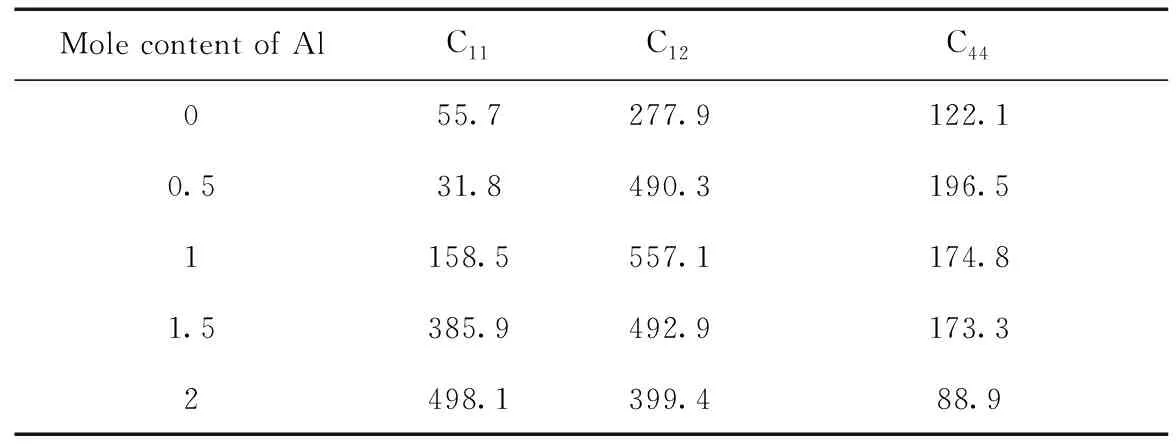
Mole content of AlC11C12C44055.7277.9122.10.531.8490.3196.51158.5557.1174.81.5385.9492.9173.32498.1399.488.9

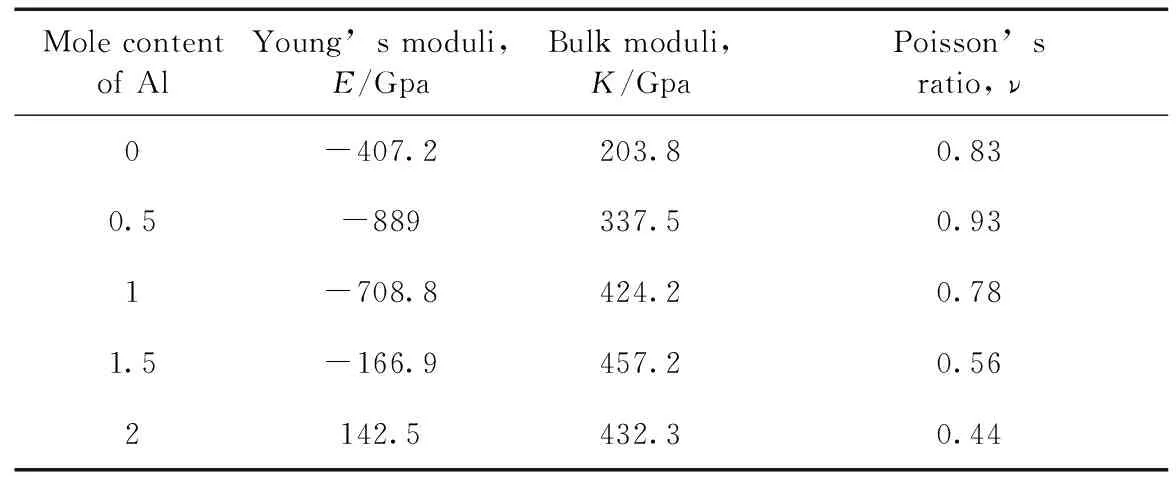
表4中列出了高熵合金AlxFeTiCrZnCu的杨氏模量E、体积弹性模量K及泊松比ν. 图3为AlxFeTiCrZnCu高熵合金的杨氏模量E与体积弹性模量K随着Al元素摩尔含量的变化. 由表4和图3可以看出，随着Al元素摩尔含量的增加，高熵合金AlxFeTiCrZnCu的体积弹性模量先增大后减小，在Al元素摩尔含量为1.5时体积弹性模量最大，为457.2GPa；杨氏模量在Al元素摩尔含量较小时皆为负值，说明Al元素含量小时，高熵合金的结构并不稳定.

表4 高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)的杨氏模量E、体积弹性模量K及泊松比ν

Table 4 Young’s moduli (E), bulk moduli (K), and Poisson’s ratios (ν) of the high entropy alloys AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)

Mole contentof AlYoung’s moduli,E/GpaBulk moduli,K/GpaPoisson’sratio, ν0-407.2203.80.830.5-889337.50.931-708.8424.20.781.5-166.9457.20.562142.5432.30.44

图3 高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)的杨氏模量E、体积弹性模量K与Al元素摩尔含量的关系Fig. 3 Relationships of Young’s moduli (E) and bulk moduli (K) to the mole content of Al for the high entropy alloys AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)

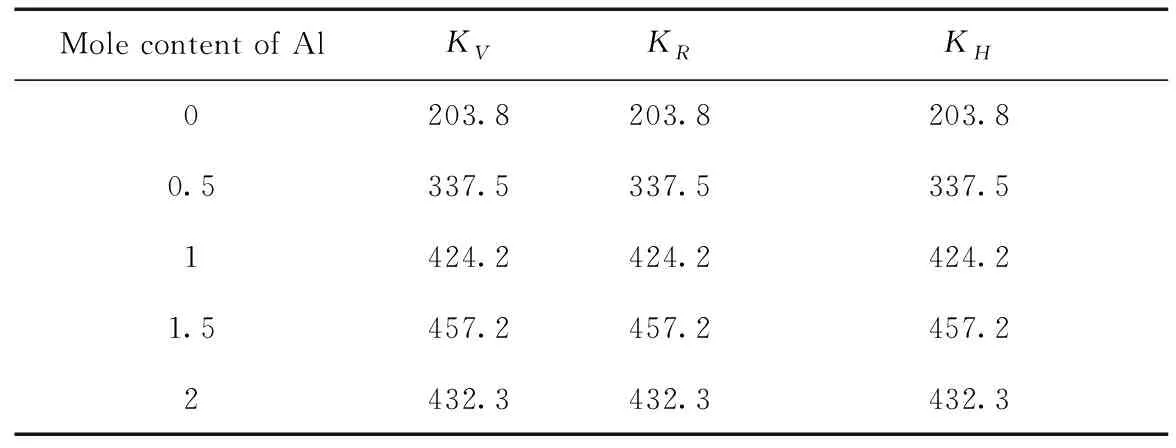
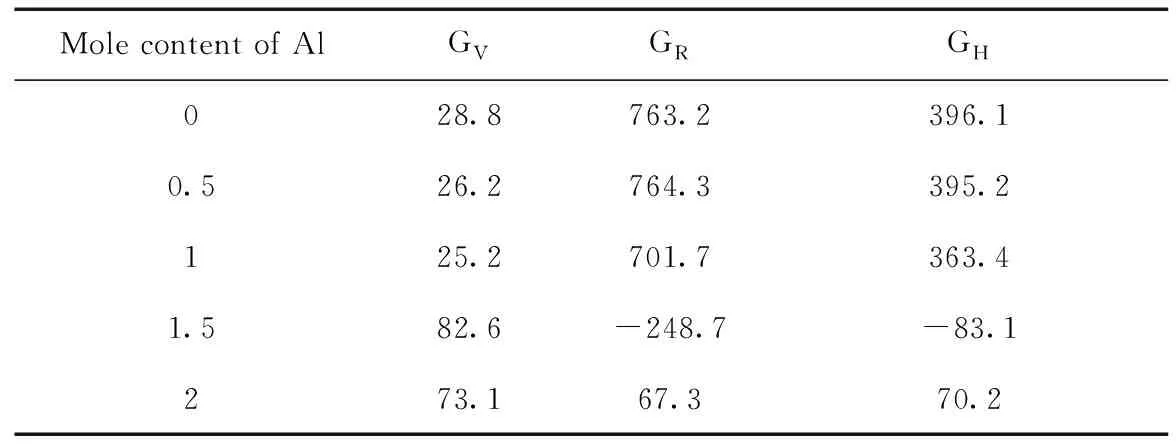
为了进一步了解高熵合金AlxFeTiCrZnCu的力学性能，本文又采用Voigt-Reuss-Hill (VRH)的方法[26]计算了体积弹性模量KV、KR、KH和剪切模量GV、GR、GH，计算结果列于表5和表6中. 由表5和表6中的计算结果明显可以看出，采用VRH方法计算AlxFeTiCrZnCu高熵合金的体积弹性模量并无多大变化，而剪切模量的计算结果存在较大差异.

表5 采用VRH方法计算高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)的体积弹性模量K(Gpa)

Table 5 Bulk moduli for the high entropy alloys AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2) by VRH approximations (Gpa)

Mole content of AlKVKRKH0203.8203.8203.80.5337.5337.5337.51424.2424.2424.21.5457.2457.2457.22432.3432.3432.3

表6 采用VRH方法计算高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)的剪切模量G (GPa)

Table 6 Shear moduli for the high entropy alloys AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2) by VRH approximations (GPa)

Mole content of AlGVGRGH028.8763.2396.10.526.2764.3395.2125.2701.7363.41.582.6-248.7-83.1273.167.370.2

此外，金属材料的脆/韧性取决于金属材料的泊松比或是剪切模量与体积弹性模量的比值. 金属材料的泊松比为1/3左右时可视其为韧性材料，其余为脆性材料[27]；剪切模量与体积弹性模量的比值为0.57是金属材料脆/韧性的分界点；当比值大于0.57时，视其为脆性材料；比值小于0.57时，视其为韧性材料[28]. 表7列出了高熵合金AlxFeTiCrZnCu的泊松比及剪切模量与体积弹性模量的比值. 由表7列出的计算结果可以看出，当以泊松比为判定依据时，高熵合金AlxFeTiCrZnCu无论如何改变Al元素含量都是脆性材料；而以剪切模量与体积弹性模量的比值为判定依据时，只有在Al元素摩尔含量为2时高熵合金才为韧性材料，其余皆为脆性材料. 可以发现当金属材料的脆/韧性判定依据不同时，高熵合金本身的脆/韧性也不同，这可能是由于泊松比是材料横向应变与纵向应变比值的绝对值，是一种反应材料横向变形的系数，因此采用泊松比为判据时材料的脆/韧性与采用其它判据时结果不同.

表7 高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)的泊松比及剪切模量与体积弹性模量的比值

Table 7 Calculated Poisson’s ratios, ratios of shear moduli to bulk moduli for the high entropy alloys AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2)

Mole content of AlPoisson’s ratio, νG/K00.831.940.50.931.1710.780.851.50.56-0.1820.440.16

3.3 生成热

在优化了高熵合金AlxFeTiCrZnCu及高熵合金包含的各个金属元素单质的晶格结构之后，得到了高熵合金AlxFeTiCrZnCu的基态总能量及平衡晶格结构. 本文中高熵合金AlxFeTiCrZnCu的生成热可由下式算出：

Eform=Etotal-(∑xeleEele)/(∑xele)

(2)

式中，Eform为高熵合金AlxFeTiCrZnCu的生成热，Etotal为高熵合金AlxFeTiCrZnCu的基态总能量，xele和Eele分别是是金属元素单质的摩尔分数和平衡晶体结构下的单原子总能量. 高熵合金AlxFeTiCrZnCu的基态总能量及采用公式(2)计算的高熵合金AlxFeTiCrZnCu的生成热列于表8中，生成热随着Al元素摩尔含量的变化如图4所示.

表8 高熵合金AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2, 3)的基态总能量和生成热

Table 8 The total energies (eV) and the heats of formation (kJ/mol) for the high entropy alloys AlxFeTiCrZnCu(x=0, 0.5, 1, 1.5, 2, 3)

Mole content of AlTotal energyHeat of formation0-531.5-122420.5-437.9-66351-370.6-29911.5-323.2-7652-288.16243-240.91677

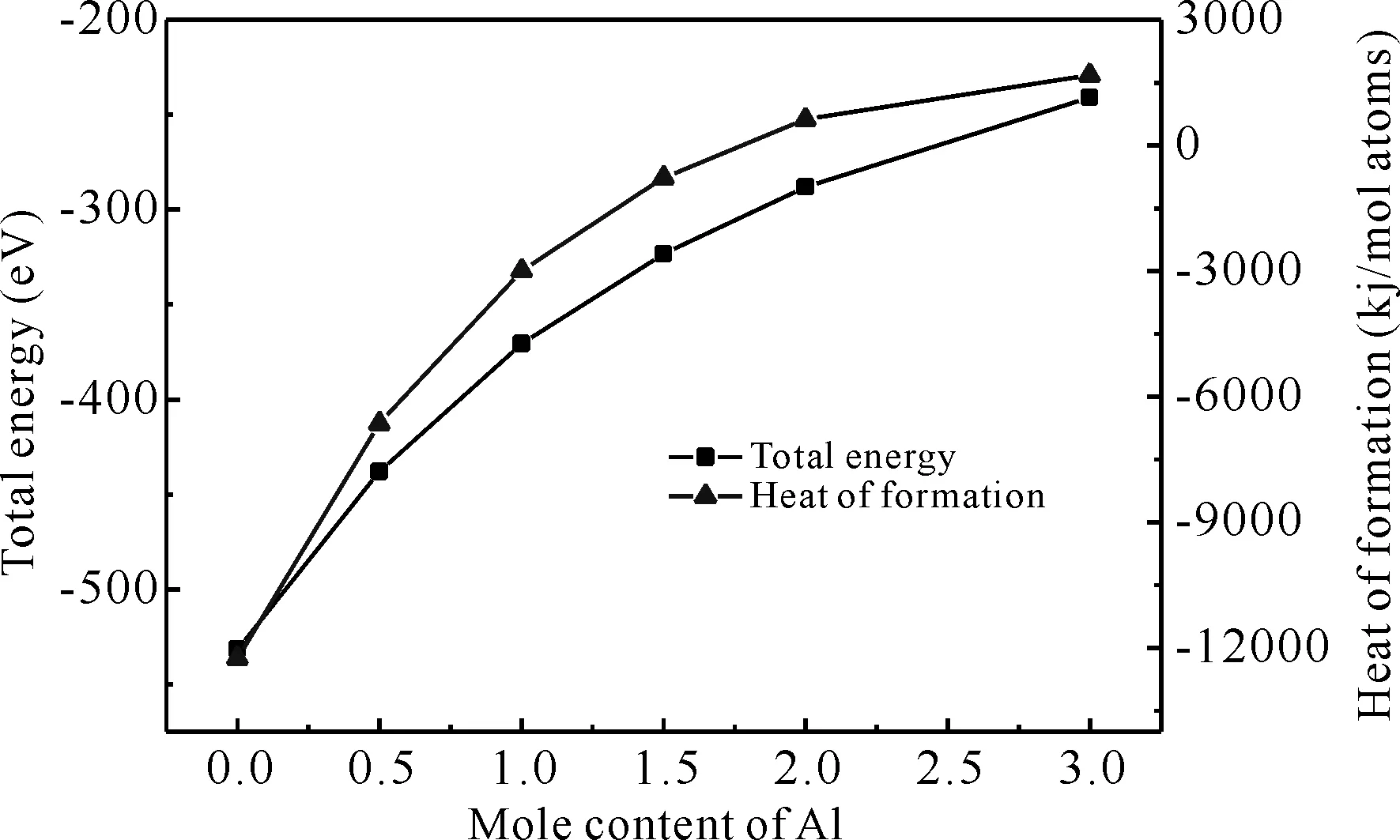
图4 高熵合金AlxFeTiCrZnCu的基态总能量及生成热与Al元素摩尔含量的关系Fig. 4 Relationship between the total energy and the heat of formation for the high entropy alloysAlxFeTiCrZnCu (x=0, 0.5, 1, 1.5, 2)

由于金属材料的热力学稳定性由其吉布斯自由能决定，吉布斯自由能是金属材料的熵与生成热的和. 但是本文所采用的第一性原理密度泛函理论是从头计算原则，计算设置为理想条件的0K下，并没有考虑熵的影响，因此在本文的计算设置参数下生成热就决定了高熵合金AlxFeTiCrZnCu的热力学稳定性. 由表8中的计算结果可以看出，高熵合金AlxFeTiCrZnCu的基态总能量均为负值；而生成热随着Al元素摩尔含量的增加由负值增加为正值. 由图4可以看出高熵合金AlxFeTiCrZnCu的基态总能量和生成热都是随着Al元素摩尔含量的增加而增大的，但是基态是指在正常状态下，原子处于最低能级时电子在离核最近的轨道上运动的定态，基态能量的大小体现了系统的稳定性. 因此对于高熵合金AlxFeTiCrZnCu来说Al元素含量越小基态总能量越小，其合金体系相比于其它合金系稳定. 而且Al元素摩尔含量增大的同时生成热逐渐增大为正值了，说明其热力学不稳定，因此无论从合金系的稳定性还是从热力学角度来考虑AlxFeTiCrZnCu高熵合金的Al元素摩尔含量都不是越多越好.

4 结 论

1)高熵合金AlxFeTiCrZnCu的密度随着Al元素含量的增加而逐渐减小，晶格常数在Al摩尔含量为1时最小.

2)高熵合金AlxFeTiCrZnCu只有在Al元素摩尔含量为2时才符合力学稳定性判据；以泊松比为判定依据时，高熵合金AlxFeTiCrZnCu皆为脆性材料，以剪切模量与体积弹性模量的比值为判定依据时，AlxFeTiCrZnCu高熵合金只有在Al元素摩尔含量为2时高熵合金才为韧性材料，其余皆为脆性材料.

3)在本文所设置的计算条件下，AlxFeTiCrZnCu高熵合金系的稳定性会随着Al元素含量的增加而不稳定，并且热力学稳定性也随之降低.