BeCl2分子的低能电子弹性散射研究

李 雪， 王怡文， 张浩兴， 王克栋

(河南师范大学物理学院， 新乡 453007)

1 引 言

电子-分子碰撞是研究分子结构与动力学的重要手段, 同时，该过程广泛存在于辐射物理学，天体物理学，聚变科学，等离子体蚀刻等领域. 比如在聚变反应和等离子体物理学中，电子与原子、离子、分子的碰撞数据在等离子体诊断中起着非常重要的作用. 自2002年铍被推荐为ITER(国际热核能源反应堆)项目中高温等离子体装置部件的材料[1]，铍和铍化合物的碰撞过程及散射截面数据引起人们的兴趣. 2003年，Colgan等人采用微扰畸变波方法计算了Be，Be+，Be2+，Be3+的基态和第一激发态的电离截面[2]. 在2010年，Hehr等人基于从头算方法报道了Be2C的散射截面并利用NJOY代码计算了其非弹性散射截面[3]. 2011年Chakrabarti 和Tennyson用R矩阵方法计算了e-BeH+的散射截面，报道了存在的Feshbach共振态[4]. 2017年，Darby-Lewis等人基于R矩阵方法研究报道了BeH的电子碰撞激发截面和共振态[5]. BeCl2是铍化合物的一种，可用于制备有机铍化合物和金属铍，还可作为有机合成的催化剂，应用于离子极化力连接性拓扑指数的研究[6]，BeCl2还可作为芳基-甲基醚脱烷基化的新型高选择性试剂[7]. 由于它在这些方面的重要性，人们已经研究了BeCl2的电子结构. Hildenbrand等人采用飞行质谱研究了BeCl2的解离能[8]；Girichev等人利用电子衍射结合质谱数据研究了BeCl2蒸气的分子结构[9]；BeCl2还被用于研究重离子对诱发卫星X射线发射的影响[10]等. 尽管已经有一些对BeCl2的研究，但是据我们所知，目前尚没有研究报道该分子的低能电子散射结果.

本文运用UK分子的R矩阵代码[11, 12]，理论研究BeCl2分子的低能电子弹性散射过程. 在具体的研究过程中，依次构建了静态交换势模型(SE)，静态交换加极化势模型(SEP)和密耦合模型(CC)，探测可能形成的势形共振态，研究了BeCl2分子的微分散射截面(DCS)和动量转移截面(MTCS). 理论计算结果不仅为天体物理和等离子体物理提供重要的截面数据，而且为低能电子碰撞实验和解离性电子贴附实验提供有益的参考和理论依据. 本文的内容安排如下：文章的第二部分，将介绍理论研究的细节；文章的第三部分，将详细分析讨论此次计算得到的数据；文章的第四部分，将对此次的研究成果做简要的总结.

2 计算细节

2.1 理论计算方法

Burke等人首先将R矩阵理论应用到解决原子与分子问题上[13, 14]. 随后Burke又与Muckey等人提出完整的多中心R矩阵理论[15]，目前已经广泛用于分子的低能电子散射动力学研究领域. 它的主要思想就是把组态空间分为两部分：内区和外区. 内区与外区有一个边界，而R矩阵就是联系内区与外区的边界条件. 内区包含在一个球体内，其球心为靶分子的质心，半径为R，通常所选半径为12到18个波尔半径，本次计算工作选取的是12个波尔半径. 靶分子(包含N个电子)的电子云几乎全部包含在内区，由于内区里靶分子的电子与散射电子不可区分，所以必须考虑电子间的短程交换和相关效应，而且短程相关效应对于准确预测大散射角下的微分截面至关重要. 在内区构建波函数时采用密耦合近似，而基于此近似，可用CI基组对内区电子波函数进行展开，如下：

(1)

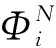
在外区，忽略靶分子电子与散射电子之间的交换和相关效应，散射电子在靶的长程多级相互作用势下运动，外区体系的总波函数可以写为：

(2)

式子中的求和是对所有的n个通道进行求和，对于一个靶分子电子态，通常会有多个通道与之相对应，这意味着即使是单态问题也会涉及到外区的多通道问题.

在内外区之间的边界处建立R矩阵，并且通过将R矩阵向外传递到足够大的半径来解决单粒子多通道问题，即可使用每个通道中的散射电子的径向波函数的渐近展开.

空间某特定方向单位立体角的散射截面变化率称为微分散射截面. 不论何种散射理论，微分散射截面对于散射数据的分析都具有重要价值. 本文运用POLYDCS程序计算微分散射截面[16]，微分散射截面的表达式如下：

(3)

公式中：AL为系数，PL为勒让德函数，B为考虑偶极相互作用的波恩近似下的相关量. 可通过将所有的末转动态|J′τ′〉求和得到任意初始转动态|Jτ〉的dσB/dΩ数值，式子如下：

(4)

动量转移截面的计算公式如下：

(5)

2.2 散射模型

对于内区，式子(1)中的第一项，可以选取靶分子的一个电子态或多个电子态包含于其中. 式子中第二项的组态L2也可以选取不同的参数进行计算处理，不同参数的选取对应着不同的散射模型. 本文采用了三种不同的散射模型：SE，SEP及CC模型. 最简单的是SE模型，该模型不考虑靶分子的极化效应，忽略极化势，靶分子的电子态波函数不随散射电子发生变化，但包含散射电子与靶分子电子之间的交换势. 通常在内区的密耦合展开中只有Hartree-Fock轨道波函数，且唯一可能的L2组态是散射电子占据到靶分子的其他非占据轨道或者虚轨道，自旋轨道. 假设靶分子的电子数为N，冻结的电子数为Nc，则此模型组态可写为：

(6)

上式表示的是N-Nc个活化电子占据靶分子的价层轨道，而散射电子占据虚轨道(VOs)中的一个. 尽管SE模型得出的共振态位置和宽度值均偏大，但它给出很清晰的物理图像. 在SE模型的基础上加上靶分子的极化效应就构成SEP模型，利用HF波函数的单电子激发来描述靶分子的极化效应，它可以给出比较精确的弹性散射截面和势形共振态结果. 此模型除了包含式子(6)描述的组态，还包括以下组态：

(7)

其中分子的芯轨道被冻结的Nc个电子占据，考虑将一个电子从价空间激发到选定的虚轨道上来描述极化效应，这些虚轨道同时也可被散射电子占据. 尽管SEP模型无法描述与靶分子的激发态有关的碰撞过程，但它能分辨Feshbach共振态，尽管预测的可靠性有待提高. 最后为CC模型，由于在内区CC展开中要包含靶分子的基态和激发态等，所以内区中非局域的交换相互作用势、靶分子的极化势以及电子的激发态过程都能给予合理的描述，由此CC近似所需的计算量比SE和SEP模型近似大很多. 此模型组态如下：

(8)

(9)

CC模型中冻结Nc个电子，N-Nc个活化电子加1个散射电子在选定数目的活化轨道中跃迁. CC模型的优点是如果Feshbach共振态的母态包含在CC展开中，该方法可预测出这个共振态；缺点是在CC展开中包含多个靶态波函数可能会出现问题，因为这些电子态波函数须采用相同的轨道波函数基组. 本文只考虑了靶基态，减少了计算难度. 本文在三种模型下具体选择的L2组态如表1所示：

表1 三种模型选择的L2组态

BeCl2分子的总电子数为38. SE模型中38个电子均占据靶分子的基态，散射电子占据一个虚轨道. SEP模型中2个芯轨道上的4个电子被冻结，17个价壳层轨道上的电子形成单空穴态，即34个电子占据价层轨道并且考虑将一个电子从价空间激发到选定的虚轨道上来描述极化效应，这些虚轨道同时也能被散射电子占据. CC模型中冻结30个电子，8个活化电子加1个散射电子在8个活化轨道中跃迁.

2.3 形状共振态

在散射过程中，电子会被靶分子短暂的捕获，形成一个准束缚态或者寿命比较短的态，称为共振态，此共振态不稳定，会通过各种各样的方式衰退掉. 对共振态的形成机制的研究是了解电子分子散射过程的关键所在. 定性上，共振态可以根据类型和组态进行分类；定量上，可以通过确定共振态的对称性、位置、宽度来确定一个共振态. 形状共振态是最简单的共振态，这个共振态中，散射电子被一个电子分子相互作用势中的势阱所捕获. 通常情况下，这个势阱是通过吸引的极化势与排斥的离心势互相叠加而形成的. 离心势是由入射电子的角动量引起的，因此，角动量为零的s波不会形成共振态. 从量子化学的观点来看，形状共振态就是散射电子占据到基态靶分子的最低非占据轨道上. 靶分子的基态就是形状共振态的母态，形状共振态的能量高于中性靶分子基态的能量，它可以衰退到它的母态上，同时释放出一个电子. 形状共振态的寿命比较低，在散射截面上表现为一个相对较宽的峰.

3 计算结果与分析

BeCl2为闭壳层非极性直线型分子，属于D∞h点群. 由于其对称性很高，在具体计算时需要降低其对称性，按照D2h子群处理. 文章选用B3LYP/6-31+G**对其进行结构优化，得到Be-Cl键长均为1.8023 Å. 为了测试适合的基组，本文首先选用6-31G、cc-pVDZ和cc-pVTZ三种基组测试靶态的轨道信息，得到不同基组下靶分子的占有轨道和虚轨道信息；接着用组态相互作用方法，使用相同的虚轨道数目(16个)采用这三种不同基组依次构建SEP模型，由此计算得到的电子与BeCl2分子的弹性散射截面如图1所示. 由图可知，不同基组、相同SEP模型下预测的弹性散射截面呈现出的结构特征有差别：6-31G和cc-pVTZ基组下，散射截面中各出现一个较宽的共振峰，位置分别在1.90 eV和2.22 eV处. 在cc-pVDZ基组下该共振峰位置位于2.24 eV处，与cc-pVTZ基组预测的结果基本一致. 除此之外，cc-pVDZ基组还预测一个位置较低的共振峰位于0.30 eV，6-31G基组预测了一个位置较高的共振峰在7.37 eV处.

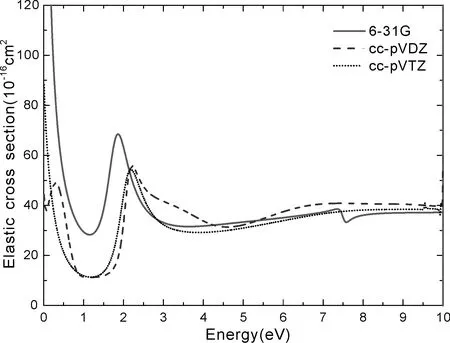
图1 不同基组、相同SEP模型下BeCl2分子的低能电子弹性散射截面Fig.1 Cross sections of elastic e-BeCl2 scattering with different basis sets in the same SEP models.

虽然活化空间选的越大，计算结果越精确，但考虑到计算条件的限制，本文在构建CC模型时，通过选取几个活化空间进行测试计算，最终选定活化空间(7,4,4,0,6,3,3,0,)进行最终计算，且只考虑靶基态，未考虑激发态通道，这使得计算大大简化. 在CC单态散射计算中，将能量较低轨道上的30个电子冻结，令剩余的8个电子和1个散射电子自由的占据6Ag-7Ag, 5B1u-6B1u, 2B2u-4B2u, 3B3u-4B3u, 3B3g和3B2g等12个分子轨道. 结果得到SE和CC模型的靶基态能量呈现于表2中. 从表2中可以看出，在两种模型中cc-pVDZ基组均预测了与cc-pVTZ基组相似的能量，因此在后续的散射计算中，我们采用计算量更小的cc-pVDZ基组，此基组下，靶分子BeCl2的基态电子态为X1Ag，基态电子组态为：

(1B1u)2(1Ag)2(2B1u)2(2Ag)2(3B1u)2(3Ag)2(1B2u)2(1B3u)2(1B3g)2(1B2g)2(4Ag)2(5Ag)2(4B1u)2(6Ag)2(5B1u)2(2B2u)2(2B3g)2(2B2g)2

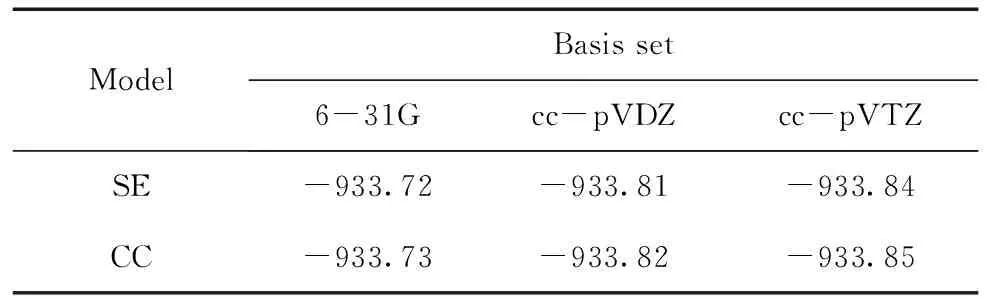
表2 BeCl2分子靶态的基态能量(eV)

图2所示为SE，SEP和CC模型下计算的弹性散射截面，包括各散射对称组分和总散射截面.

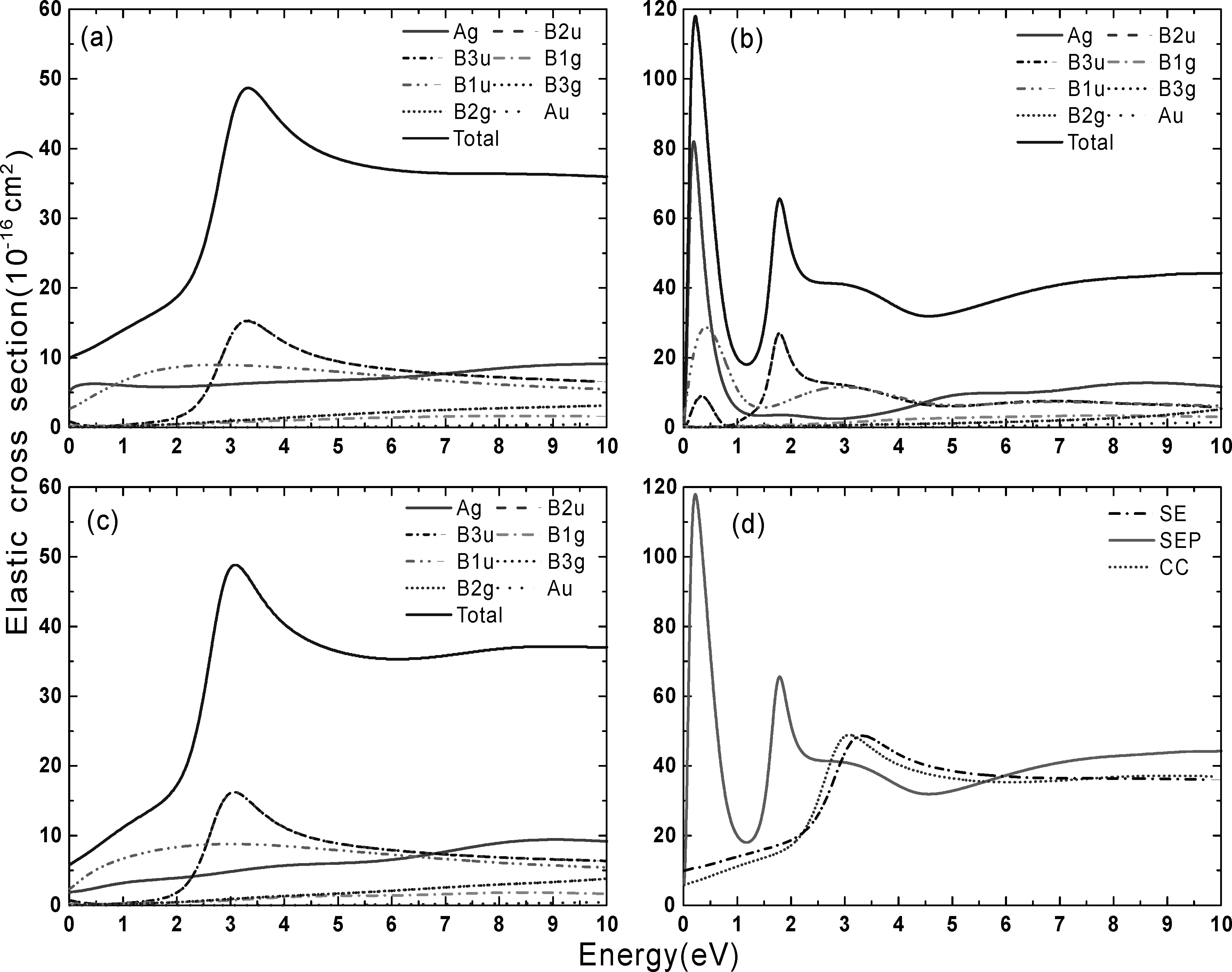
图2 弹性散射截面 (a) SE模型下的弹性散射截面；(b) SEP模型下的弹性散射截面；(c) CC模型下的弹性散射截面；(d) 三种模型下的总弹性散射截面Fig. 2 Elastic cross sections: (a) Elastic cross section in the SE model; (b) Elastic cross section in the SEP model; (c) Elastic cross section in the CC model; (d) Total elastic cross section under three models.

如图2所示，在SEP模型(虚轨道数目为31个)中，总弹性散射截面上出现了2个较宽共振峰，能量较高的共振峰在1.80 eV处，通过观察各散射对称组分的本征相移，该共振态主要来自于B2u和B3u对称性的贡献. 在SE模型中，该共振峰的位置在3.32 eV处. 我们进一步选取了8个虚轨道构建了CC单态模型，该共振态出现在3.18 eV处. SEP模型还预测了能量较低位于0.26 eV的形状共振态，它来自于B1u对称性的贡献. 但是该共振态没有被SE模型和CC模型探测到. 图2(d)比较了三种模型的弹性散射截面结果. 结果表明，SE模型出现共振态的位置均都高于SEP模型和CC模型下的位置，这种差异体现了极化效应对截面数据的影响. SE模型只考虑了靶基态，靶分子的电子都处于基态，SE模型未考虑靶分子的极化效应，一般得到的共振态位置偏高；当前CC模型同样只考虑靶基态，由于计算条件的限制，活化电子数较少，选择的活化空间较小，多通道耦合效应没有被考虑到，因此造成了SE和CC两个模型的结果很相似，这也体现了在构建CC模型时多通道耦合效应的重要性，它将对计算结果的精确度产生重要的影响. SEP模型同样只考虑靶基态，其在SE模型的基础上考虑了极化效应，并且在可以自由的选取虚轨道的数目，能方便研究极化效应对截面的影响以及探讨计算结果的收敛程度. SEP模型可以给出共振态较精确的位置和宽度，得到的截面和共振态相较于SE和当前的CC单态模型的结果更具参考价值.

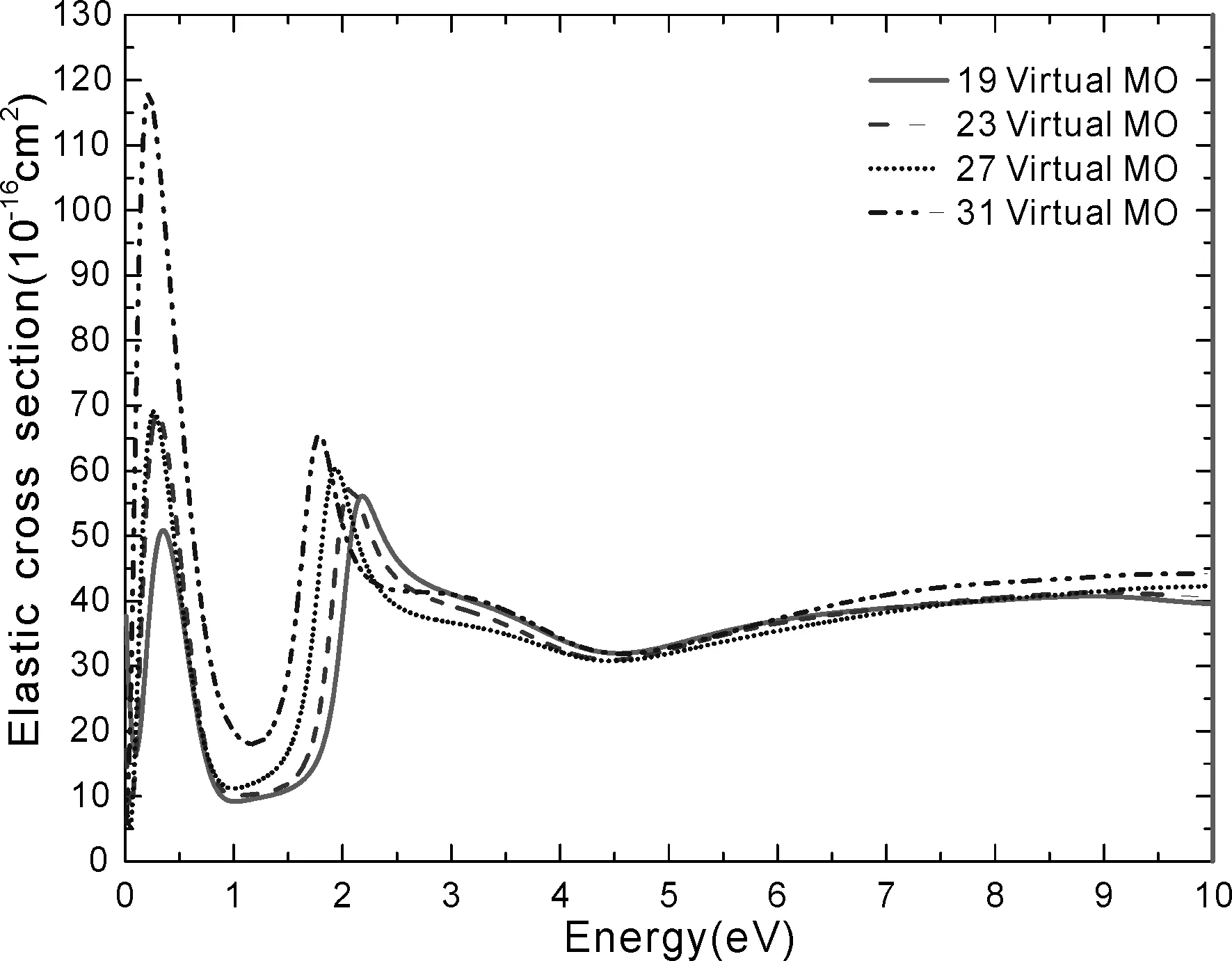
图3 SEP模型下选取不同虚轨道时计算的电子与BeCl2分子的弹性散射截面Fig. 3 Cross sections of elastic e-BeCl2 scattering with different virtual molecular orbitals in the SEP model.

为了研究极化效应对截面和共振态的影响以及讨论计算结果的收敛程度，我们构建了4个不同的SEP模型，每个模型选取不同的虚轨道，分别为：19个，23个，27个和31个虚轨道，结果如图3所示. 不同SEP模型预测的弹性散射截面均呈现相似的结构特征：都出现了两个较宽的共振峰. 选取19个虚轨道时共振峰位于0.37 eV和2.20 eV处；选取23个虚轨道时该共振峰的位置位于0.31 eV和2.09 eV处；而当选取27个虚轨道时的位置降低到0.27 eV和1.95 eV处；当选取虚轨道增加到31个时它们的位置分别继续降低到了0.26 eV和1.80 eV处. 不同SEP模型预测的共振峰位置随着虚轨道数目的增加而不断减小，这是由于增加虚轨道数目相应的增加了极化效应. 当选取31个虚轨道时，预测的能量位置较低的第一个共振态与选取27个虚轨道的结果基本一致，暗示了此时预测的结果已经接近收敛.

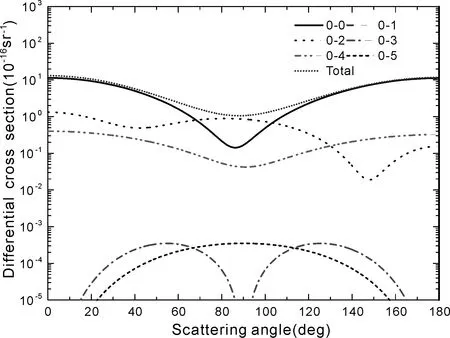
图4 入射电子能量为2 eV时的转动分辨的态-态(J→J′)微分截面Fig.4 The rotation-resolved state - to - state (J→J′) differential cross sections of the incident electron energy of 2 eV.

基于SEP模型(包含31个虚轨道)得到的K矩阵，使用POLYDCS程序[16]，我们计算了不同入射能量的DCS. 入射电子能量为2eV时BeCl2分子转动分辨的态-态微分截面如图4所示，分别给出了0→0，0→1，0→2，0→3，0→4，0→5六个组分以及这六个组分加和后的总截面. 由于BeCl2分子的较高对称性，其偶极矩为零，所以弹性散射组分0→1，0→3，0→5对总的微分截面没有贡献. 从图4中可看出，对总微分截面贡献最大的弹性散射组分为0→0，其次为组分0→2，最后为0→4. 在散射角小于68°和大于104°的时候，对总微分截面的贡献主要来自于0→0弹性散射组分，而当散射角在68°与104°之间时，组分0→2的贡献最大；尤其当散射角为86°时，0→2组分对总微分截面的贡献达到最大，此时0→0组分的贡献处于一个极小值.

如图5所示，通过对转动微分截面求和，分别给出了在入射电子能量为1、2、5和10 eV时，SE，SEP和CC三种模型下BeCl2分子的总微分截面. 三种模型下，入射能量为1 eV时DCS的变化均比较平缓. 入射能量为2 eV时，SE模型预测的DCS上出现极小值的散射角为144°，当能量增加到5 eV时，DCS的极小值出现在102°散射角，而当入射能量增加到10 eV时，极小值的位置降为96°. SEP模型下，在入射能量为2 eV，DCS的极小值出现在散射角为86°时，当能量为5 eV时，极小值出现在散射角为92°，而当入射能量增加到10 eV时，极小值的位置在86°处. CC模型下，入射能量为2 eV，DCS上出现极小值的散射角为142°，当能量为5 eV时，出现极小值的散射角则变为102°，而当入射能量增加到10 eV时，极小值的位置则降为98°，由此可见，随着入射能量的增大，CC模型下出现极小值的位置越来越低. 总的来说，随着入射电子能量增大到10 eV，三种模型预测的DCS结果已差别不大，说明极化效应随着能量的增加不再那么重要.

进一步我们计算了SE，SEP和CC三种模型下电子与BeCl2分子碰撞的MTCS(图6). 三种模型下的MTCS有差别：SE模型下在3.14 eV附近MTCS上出现了一处峰，CC模型下出现峰的位置在2.95 eV附近，SE和CC模型中出现的峰是由前文提到的B2u和B3u对称性贡献的π*形状共振态引起的；SEP模型下，选取的虚轨道不同时，共振峰出现的位置也不相同，这在前面已经详细讨论过.

4 结 论

本文通过运用R矩阵方法结合SE，SEP和CC三种模型，首次获得了电子与BeCl2分子碰撞产生的弹性散射截面，DCS和MTCS. SE模型与CC模型中各预测1个π*形状共振态，SEP模型中不同虚轨道下均出现2个π*形状共振态，由于极化效应的影响，这些共振态在不同的模型中呈现出不同的特征. 入射电子能量为2 eV时对总DCS贡献最大的弹性散射组分为0→0. 三种模型下的DCS会随着入射电子能量的增大，形状慢慢趋近相似. 在MTCS上出现的峰是由π*形状共振态引起的，其中SEP模型下出现此峰的位置与SEP模型下弹性散射截面图中出现共振态的位置吻合的非常好. 我们期待有实验研究的结果报道，当前的结果将为等离子体物理提供重要的截面数据.