采用轴对称二维模型对实际地层井间电磁响应进行成像的精确性研究

魏宝君, 任 臣, 吴康康, 党 峰

(1.中国石油大学(华东)理学院,山东青岛 266580; 2.中国石油集团测井有限公司,陕西西安 710077)

井间电磁成像技术是油气藏探测的重要手段之一,该技术将低频可移动电磁信号源置于发射井中并在周围一口或几口井中移动探测器测量感应信号,然后采用电磁成像技术将测量信号进行反演以获得井间地层电导率的分布。该技术作为地球物理探测的新方法,其探测深度更深、范围更广,是对传统单井电磁测井技术的突破,大大提高了对油气藏描述的准确性[1-2]。由于井间实际地层的电参数分布是三维的,因此最理想的井间电磁成像技术应是通过成像获得井间地层电导率的三维分布,但由于测量数据信息量的限制要想准确获得完全三维的电导率分布图像是不可能的。一般在对实际测量数据进行反演时采用轴对称二维模型进行成像,即假设电导率异常体相对于发射井呈轴对称分布,从而获得电导率在发射井—接收井剖面的二维近似分布[3-6]。由于成像模型与实际地层存在差别,因而有必要研究采用轴对称二维井间地层模型对实际地层电磁响应进行成像的精确性。笔者采用所开发的二维积分方程[7]和体积分方程[8-10]分别模拟轴对称二维井间地层和三维井间地层模型中异常体的响应,用所开发的Born迭代反演方法[7,11]通过反演不同模型的模拟数据获得发射—接收剖面的二维电导率成像,由于金属套管对井间电磁响应的影响可以消除[12-13],在模拟时假设发射井和接收井中均无金属套管;基于模拟结果分析采用轴对称二维井间地层模型实现高质量成像的可行性及影响因素。

1 基本理论

在进行数值模拟时忽略位移电流的影响并假设地层是非磁性的,其磁导率取真空中的值。水平层状背景地层的电导率设为σb,不同背景层的σb值可不同。将发射线圈视为磁偶极子并假设发射源随时间的变化关系为exp(iωt),其中ω为角频率。图1给出了轴对称二维井间地层模型和三维井间地层模型的简图,可采用积分方程进行数值模拟。

1.1 模拟轴对称二维井间地层模型响应的积分方程

所采用的轴对称二维井间地层模型见图1(a),该模型电导率异常体相对于发射井呈轴对称分布。在模拟时采用圆柱坐标系,则所有场量均只是径向坐标ρ和轴向坐标z的函数,与方位角坐标φ无关,计算区域为发射—接收剖面。接收井中接收线圈处磁场强度的轴向分量可表示为如下积分方程的形式[7]:

(1)

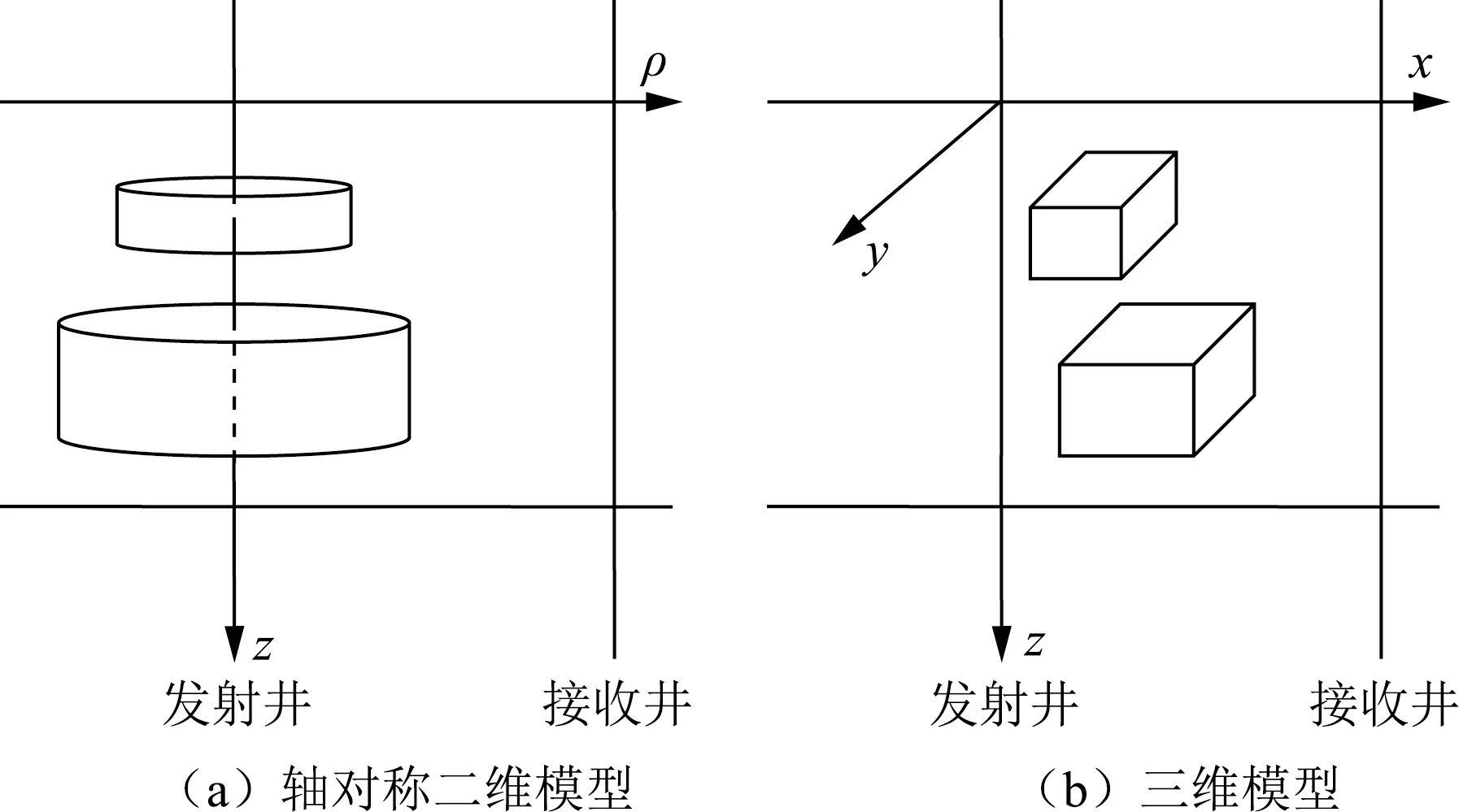
图1 井间地层模型简图Fig.1 Schematic configuration of cross-hole formation model

在积分区域D内,总电场E(r,rT)满足如下积分方程:

E(r,rT)=Eb(r,rT)+

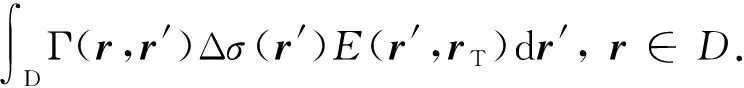
(2)

其中

Eb(r,rT)=-iωμ0NTITΓ(r,rT).

式中,Eb为电场强度的背景值;Γ(r,r′)为纵向成层背景地层磁矢势Green函数。式(2)称为目标方程,该式是计算积分区域内总电场分布的第二类Fredholm积分方程。式(2)可采用稳定型双共轭梯度(BCGS)方法进行迭代求解,从而得到总电场在积分区域D内的分布。在采用反演成像技术对井间电磁实际测量数据进行处理时一般采用轴对称二维模型进行成像,从而获得电导率在发射井—接收井剖面的二维近似分布。在该成像技术的每一步迭代过程中均将上述积分方程作为其正演算法。

1.2 模拟三维井间地层模型响应的体积分方程

对于实际地层的电导率分布情况,可采用图1(b)所示的三维井间地层模型。在模拟这种模型时采用直角坐标系,接收井中接收线圈处的磁场强度矢量可表示为如下体积分方程的形式[9]:

E(r′,rT)dr′.

(3)

式中,rT=(xT,yT,zT)、rR=(xR,yR,zR)分别为发射线圈和接收线圈的位置坐标;V为包含三维电导率异常体的积分区域;GHJ(rR,r′)为层状背景地层中r′处的单位电流元在接收点rR处的磁型并矢Green函数;E(r′,rT)为发射线圈在积分区域内产生的总电场强度矢量;Hb(rR,rT)为发射源在层状背景地层中产生的磁场强度矢量。若积分区域内总电场强度矢量E(r′,rT)已知,由该式可获得接收线圈处的磁场强度的3个分量。

在积分区域V内,总电场强度矢量E(r,rT)满足如下体积分方程:

E(r,rT)=Eb(r,rT)+(-iωμb+

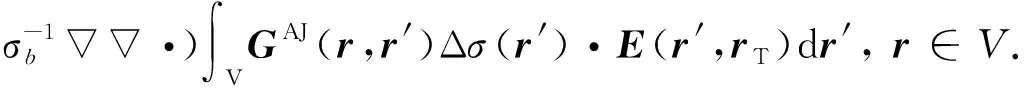
(4)

式中,GAJ(r,r′)为层状背景地层中r′处的单位电流元在场点r处的磁矢势并矢Green函数;Eb(r,rT)为发射源在层状背景地层中产生的电场强度矢量。式(4)亦可采用稳定型双共轭梯度(BCGS)方法进行迭代求解,从而得到总电场强度矢量在积分区域V内的分布。

设发射线圈的磁偶极矩为MT,则式(3)和式(4)中发射源在背景地层中产生的电场强度矢量和磁场强度矢量可表示为

Eb(r,rT)=GEM(r,rT)·MT,

(5)

Hb(rR,rT)=GHM(rR,rT)·MT.

(6)

式中,GEM和GHM分别为水平层状背景地层中单位磁偶极子源产生的电型和磁型并矢Green函数。

1.3 轴对称二维井间地层模型的成像方法

在成像过程中,假设所采集到的数据点的总数目为M,成像区域D被离散为N个相同单元,每个单元内的总电场强度和电导率均恒定,则式(1)经离散后可表示为如下形式:

f=M·x.

(7)

式中,f为M维复列矢量,其元素由测量到的散射磁场的轴向分量构成,本文中用于成像的测量数据既可以根据三维井间地层模型由体积分方程模拟得到,也可以根据轴对称二维井间地层模型由二维积分方程模拟得到;x为由未知电导率差值构成的N维实列矢量;M为M×N维复矩阵,其各元素的具体表达式可由式(1)的离散形式得到。

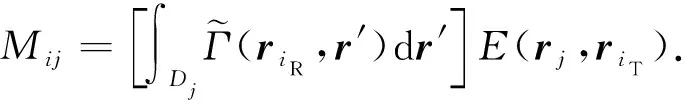
(8)

式中,iT为发射源位置序号;iR为接收器位置序号,发射源位置总数与接收器位置总数的乘积即为数据点总数目M;j为成像单元的序号,j=1,…,N。

由于式(8)中总电场强度依赖于x,因而矩阵M亦依赖于x,故式(7)的反演是一个非线性问题;又由于在一般情况下测量数据的信息量相对于未知量而言是非常有限的,故式(7)的反演结果一般是不唯一的。反演式(7)可通过采用Born迭代方法(BIM)实现,该方法具有反演过程稳定的优点[11]。在BIM的第n+1步迭代中可通过使下列正则化成本函数最小化获得x的近似值xn+1:

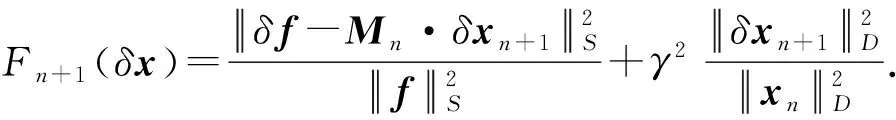
(9)

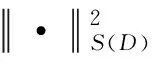
(10)

式中,上标“+”表示复共轭转置。求解式(10)采用正则化最小二乘法实现。

2 正演数值模拟对比

无论是轴对称二维井间地层模型,还是三维井间地层模型,其背景地层是相同的,发射源在背景地层中产生的磁场强度的轴向分量也相同,区别只在于电导率异常体产生的散射场差异有多大,故在通过数值模拟对这两种模型的散射场进行对比时假设背景地层为均匀介质。

2.1 异常体沿y方向厚度变化时的影响

图2为井间地层模型1,所采用的发射频率为1 kHz,在井间区域有两个相对低电导率异常体,其电导率自上而下分别为0.05和0.01 S·m-1。对轴对称二维模型,异常体相对于发射井呈圆周对称;对三维模型,异常体沿垂直于纸面方向(y向)居中放置,即相对于y=0平面保持对称,但沿y方向的厚度Δy可不同。在模拟时,固定发射源位于轴向坐标zT=0处,接收器在接收井中沿井轴方向在-100 m至100 m间移动。图3给出了该模型二维和三维情况下散射磁感应强度Bs的轴向分量随接收器轴向坐标zR变化时的对比结果,并给出了不同厚度三维异常体散射场与二维异常体散射场的平均误差,其中三维异常体沿y向的厚度Δy共取9种数值。

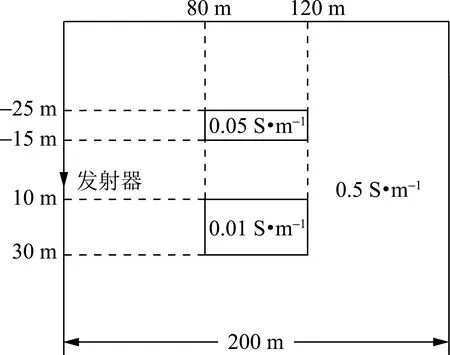
图2 地层模型1Fig.2 Formation model 1

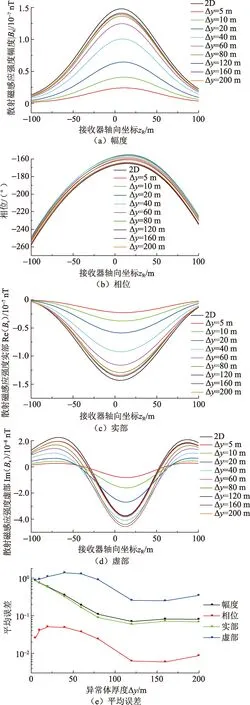
图3 地层模型1数值模拟结果Fig.3 Numerical simulation results for formation model 1

由图3(a)和图3(e)可以看出,当三维异常体沿y方向的厚度较小时,其产生的散射场的幅度与二维异常体产生的场相比要小得多,平均误差也较大,这主要是三维异常体体积太小导致的。随着Δy的增加,三维异常体产生的散射场的幅度逐渐增加,越来越接近轴对称二维异常体产生的散射场,平均误差亦逐渐减小,但在该模型中其散射场最大值并没有达到后者的散射场。当Δy增加到一定数值时(对本模型约是120 m),三维异常体产生的散射场幅度达到最大值,其后再增加Δy其散射场幅度无明显改变,平均误差亦无明显变化。由图3(b)和图3(e)可以看出,该模型两类异常体散射场相位的差异小于幅度的差异,平均误差最小。当Δy在很小值(5 m)的基础上增加时,首先出现三维异常体散射场相位逐渐偏离轴对称二维异常体散射场相位的情况,平均误差亦相应增加。其后二者再逐渐接近,平均误差亦随Δy的增加而逐渐减小。其后再增加Δy,其散射场相位虽稍有增加,但无明显改变,平均误差亦无明显变化。图3(c)中散射场实部随Δy的变化规律与图3(a)的变化规律类似,其平均误差随Δy的变化规律亦相似。由图3(d)和图3(e)可以看出,两类异常体散射场虚部的差异较大,平均误差亦较大,平均误差随Δy变化的规律类似于散射场相位的变化规律。由于在接收器轴向坐标zR连续改变时散射场虚部出现符号变化,且其强度远小于实部分量,故该分量相对误差较大。

模型2在井间区域有两个相对高电导率异常体,其电导率自上而下分别为20 和10 S·m-1,其余参数及测量方式同模型1。图4为该模型二维(2D)和三维情况下散射磁感应强度轴向分量随接收器轴向坐标zR变化时的对比结果,并给出了不同厚度三维异常体散射场与二维异常体散射场的平均误差,三维异常体沿y向的厚度Δy亦取上述9种数值。

由图4(a)可得到与图3(a)相同的结论,只是平均误差最小值对应的Δy约为160 m。由图4(b)和(e)可知,当Δy较小时,三维异常体散射场的相位与二维异常体散射场的相位相比差别较大,平均误差也较大。随着Δy的增加,三维异常体散射场的相位逐渐减小,越来越接近二维异常体散射场的相位,平均误差亦逐渐减小,到Δy为160 m时达到最小,其后变化较缓慢。由图4(c)和(e)可看出,当Δy较小时,两类异常体散射场实部的差异较大,平均误差亦较大。当Δy在很小值(5 m)的基础上增加时,首先出现三维异常体散射场实部逐渐偏离轴对称二维异常体散射场实部的情况,平均误差亦相应增加。其后二者再逐渐接近,平均误差亦随Δy的增加而逐渐减小。其后再增加Δy其散射场实部虽稍有增加但改变较小。该模型由于在接收器轴向坐标zR连续改变时散射场实部出现符号变化,故相对误差较大一些。图4(d)中散射场虚部随Δy的变化规律与图4(a)的变化规律更为接近,其平均误差随Δy的变化规律亦相似。

综合上述两种模型的计算结果可以看出,在将三维地层环境中得到的井间测量数据在发射—接收剖面采用轴对称二维模型进行成像时其成像结果的质量与异常体沿y方向的厚度Δy有关。若异常体沿y方向厚度较小,其产生的散射场与二维异常体产生的散射场相比要小,平均误差较大,成像效果与实际模型相比差别较大。三维异常体沿y方向尺寸越大,误差越小,成像效果越接近于真实情况,但当Δy增加到一定数值后再增加厚度时成像效果改善不大。上述结果也说明,接收器所接收到的电磁信号主要来自于发射—接收剖面附近地层的贡献,越偏离该剖面,地层对信号的贡献越小。

图4 地层模型2数值模拟结果Fig.4 Numerical simulation results for formation model 2

2.2 异常体沿y方向平移的影响

模型3为模型1取三维电导率异常体的厚度Δy为120 m时得到,并假设三维异常体沿y方向可以平移,其中心点坐标yc可变化。图5为该模型异常体为二维轴对称(2D)和三维分布情况下散射磁感应强度轴向分量随接收器轴向坐标zR变化时的对比结果,并给出了不同的中心点坐标yc对应的三维异常体散射场与二维异常体散射场的平均误差,其中三维异常体中心点坐标yc共取11种数值。

由图5(a)和(e)可以看出,当三维电导率异常体沿y方向偏心程度较低即中心点坐标yc较小时(对本例yc可到20 m),其产生的散射场的幅度与异常体居中时散射场的幅度无明显差别,与二维异常体产生的散射场幅度较为接近,平均误差也较小。其后随着偏心程度的增加,三维异常体产生的散射场的幅度逐渐减小,越来越偏离轴对称二维异常体产生的散射场,平均误差亦随之增大。由图5(b)和(e)可以看出,三维异常体沿y方向偏心程度对其散射场相位的影响远小于对幅度的影响,在yc<60 m的范围内散射场的相位无明显改变,平均误差也较小。只有当yc达到70 m之后相位的变化才逐渐明显,相位逐渐落后,平均误差亦随之增大。图5(c)中散射场实部随yc的变化规律与图5(a)的变化规律类似,其平均误差随yc的变化规律亦相似。由图5(d)和(e)可看出,由于在接收器轴向坐标zR连续改变时散射场虚部出现符号变化且其强度远小于实部分量,两类异常体散射场虚部的平均误差较大,平均误差随yc变化的规律类似于散射场相位的变化规律。在yc<40 m的范围内散射场的虚部改变不明显。

模型4为模型2取三维电导率异常体的厚度Δy为160 m时得到,并假设三维异常体沿y方向可以平移,其中心点坐标yc可变化。图6为该模型异常体为二维轴对称和三维分布情况下散射磁感应强度轴向分量随接收器轴向坐标zR变化时的对比结果,并给出了不同的中心点坐标yc对应的三维异常体散射场与二维异常体散射场的平均误差,其中三维异常体中心点坐标yc亦取11种数值。

由图6(a)和(e)可得到与图5(a)相似的结论,对本例当yc<40 m时三维异常体产生的散射场的幅度与二维异常体产生的散射场幅度较为接近。由图6(b)和(e),该模型三维异常体沿y方向偏心程度对其散射场相位的影响既小于对幅度的影响也小于对模型3中相位的影响。由图6(c)和图6(e)可以看出,该模型由于在接收器轴向坐标zR连续改变时散射场实部出现符号变化,在yc较大时两类异常体散射场实部的平均误差较大,平均误差随yc变化的规律类似于散射场相位的变化规律。在yc小于50 m的范围内散射场的实部改变不明显。图5(d)中散射场虚部随yc的变化规律与图5(a)的变化规律类似,其平均误差随yc的变化规律亦相似。

图6 地层模型4数值模拟结果Fig.6 Numerical simulation results for formation model 4

综上所述两种模型的计算结果可以看出,在将三维地层环境中得到的井间测量数据在发射—接收剖面采用轴对称二维模型进行成像时,其成像结果的质量与异常体沿y方向的偏心程度有关。在厚度Δy足够大且不变的前提下,若异常体沿y方向偏心程度较低,其产生的散射场与二维异常体产生的散射场相比较为接近,平均误差较小,成像效果越接近于真实情况。三维异常体沿y方向偏心程度越大,相对误差越大,成像效果越偏离真实情况。

2.3 异常体沿x方向平移的影响

模型5中井间区域有两个相对高电导率异常体,其电导率自上而下分别为20 和10 S·m-1,其余参数及测量方式同模型1。三维异常体沿y方向的厚度Δy为较小值20 m、中心点坐标yc=0 m。无论是轴对称二维异常体还是三维异常体均可在发射—接收剖面沿x方向移动,其中心点坐标xc共取8种数值。图7给出了当异常体沿x方向中心点坐标xc取不同的值时轴对称异常体(2D)和三维异常体(3D)的散射场随接收器轴向坐标zR的变化关系。

对比图7(a)和(b)可以看出,由于三维异常体沿y方向的厚度较小,其散射场幅度的极大值要小于轴对称异常体产生的散射场幅度的极大值。随着xc的变化,轴对称异常体产生的散射场幅度的极大值变化不大,而三维异常体产生的散射场幅度的极大值出现较大变化。随着xc的增加,三维异常体产生的散射场幅度的极大值逐渐减小,在xc=100 m即井间距的一半时达到最小,其后又逐渐增大。这说明在厚度Δy较小时,中心点坐标xc越接近发射—接收井中间位置,三维异常体产生的散射场的幅度与二维异常体产生的磁场相比越小,平均误差也越大。对比图7(c)和(d)可以看出,由于xc改变导致的轴对称异常体和三维异常体散射场相位的变化规律相似,但二者存在一定的相位差。对比图7(e)和(f)中散射场的实部、图7(g)和(h)中散射场的虚部,可以得到与散射场幅度相似的结论。

图7 地层模型5数值模拟结果Fig.7 Numerical simulation results for formation model 5

3 成像结果对比

基于上述数值模拟得到的分析结果,对实际成像效果进行对比。在图8所示的井间地层模型中有两个相对高电导率异常体,所采用发射频率为1 kHz。在模拟成像所需的测量数据时设发射源在发射井中的垂向移动范围为-50～50 m,移动间隔为5 m,则发射源位置共为21个。接收器在接收井中的垂向移动范围、间隔与发射源相同,接收器位置共计也为21个,故数据点的总数目即信息量数目为M=441。在模拟时可分别假定待成像的电导率异常体相对于发射井轴呈轴对称分布、沿y方向以不同厚度居中或偏心分布,而在利用这些模拟的测量数据进行成像时均采用轴对称模型,即在成像时无论异常体的实际形状如何均假设其相对于发射井呈轴对称分布，从而实现在发射—接收剖面的二维成像。在该模型中井间成像范围设定为水平方向0～100 m、垂向-50～50 m,每个成像单元的尺寸为5 m×5 m,则成像单元的总数目为N=400。

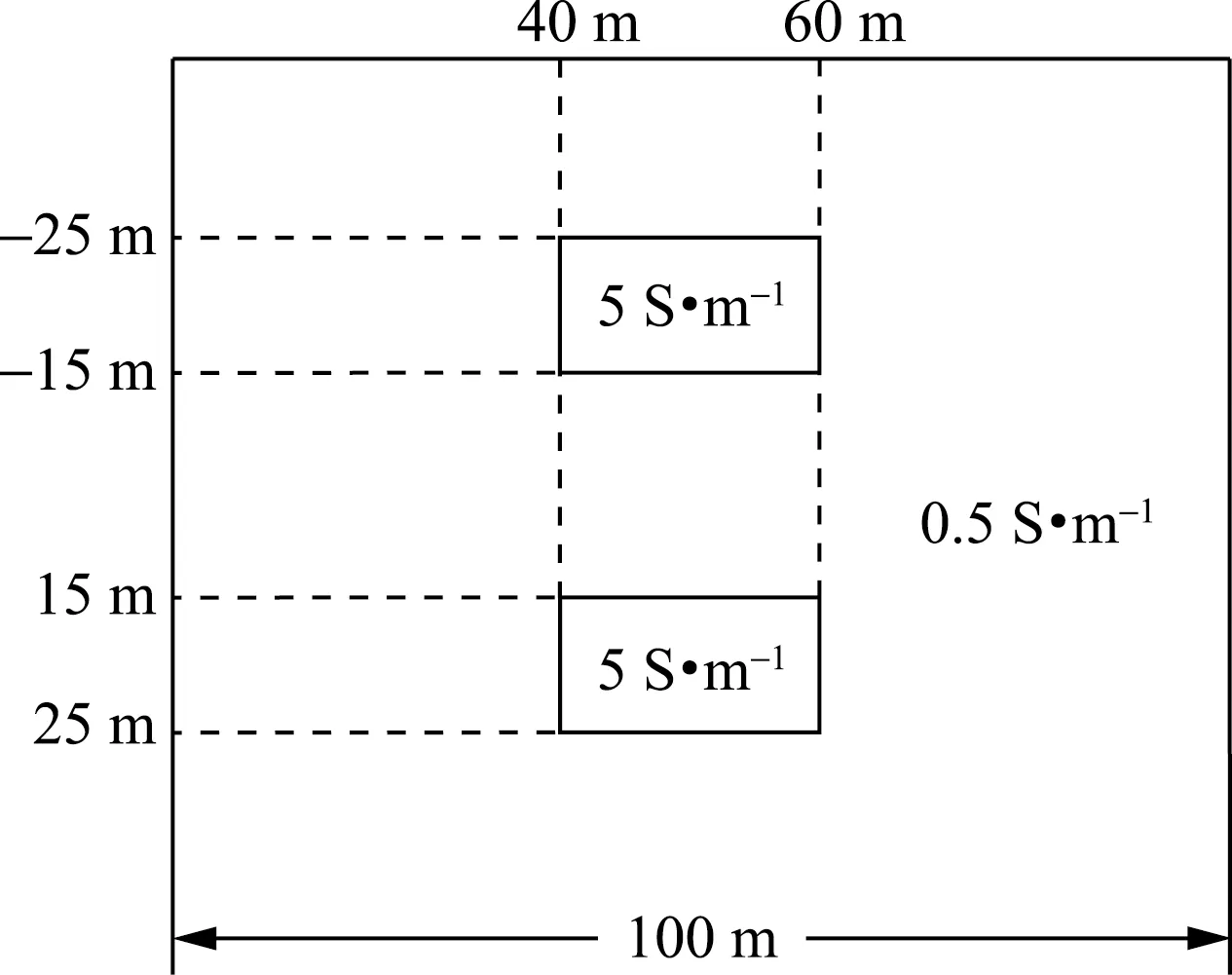
图8 成像模型Fig.8 Imaging model

图9(a)为实际异常体相对于发射井轴呈轴对称时的剖面成像结果,由于异常体的实际分布方式与成像所采用的轴对称模型是相同的,故成像结果与原模型最为接近,无论是分布范围还是异常体的电导率数值均具有较好的成像效果。图9(b)为实际异常体为三维异常体、沿y方向居中且厚度较大(yc=0 m、Δy=80 m)时的成像结果。根据前面分析,此时三维异常体产生的散射场与轴对称二维异常体产生的散射场虽有差别但较为接近,故从该图也能得到较为理想的成像结果,但无论是分布范围还是异常体的电导率数值均不如图9(a)精确。图9(c)为三维异常体沿y方向居中且厚度较小(yc=0 m、Δy=40 m)时的成像结果,图9(d)为三维异常体沿y方向偏心(yc=40 m、Δy=80 m)时的成像结果。这两种情况下三维异常体产生的散射场与轴对称二维异常体产生的散射场差别较大,成像质量均不如图9(b),与前面分析结论也是一致的。由图9的成像结果可以看出,只要异常体沿y方向厚度足够大、其中心点距离发射—接收剖面较近,是可以采用轴对称二维模型实现较高质量成像的。异常体沿y方向厚度越小、偏心程度越大,成像效果越差。

图9 成像结果对比Fig.9 Comparison of imaging results

4 结 论

(1)将三维地层环境中得到的井间测量数据在发射—接收剖面采用轴对称二维模型进行成像时，其成像质量与异常体沿垂直于发射—接收剖面方向的厚度有关。若异常体厚度较小,其产生的散射场与二维异常体产生的散射场相比要小,成像效果与实际模型相差较大。厚度越大,成像效果越接近于真实情况,但当厚度增加到一定数值后再增加厚度时成像效果变化不大。

(2)将三维地层环境中得到的井间测量数据在发射—接收剖面采用轴对称二维模型进行成像时,其成像质量与异常体沿垂直于发射—接收剖面方向的偏心程度有关。在厚度足够大的前提下,若异常体偏心程度较低,其产生的散射场与二维异常体产生的散射场相比较为接近,成像效果越接近于真实情况。偏心程度越大,成像效果越偏离真实情况。

(3)三维异常体在发射—接收剖面水平方向中心点坐标越接近于发射—接收井中间位置,其产生的散射场的信号强度越小。

(4)只要异常体沿垂直于发射—接收剖面方向的厚度足够大,其中心点距离发射—接收剖面较近,是可以采用轴对称二维模型实现高质量成像的。异常体厚度越小,偏心程度越高,成像效果越差。