基于RBFNN与信息融合的电驱动系统故障诊断系统研究
2020-04-25柳炽伟景玉军孙文中
柳炽伟, 景玉军, 李 军, 孙文中
(中山职业技术学院 机电工程学院, 广东 中山 528403 )
电动汽车采用的动力电源电压大多在300 V以上,对车辆使用的安全性提出更高的要求,需要维护部门具备较强的电动汽车故障检测与诊断技术。当前许多电动汽车运营企业的维修技术力量不足,车辆故障的检测与诊断过分依赖于系统供应商的售后服务,影响了车辆使用可靠性和经济性[1]。为提高企业车辆运营效益,加快电动汽车诊断技术人员培养,开发智能化的故障诊断系统具有重要的现实意义。
1 汽车电驱动系统故障分析
纯电动汽车驱动系统的故障模式包括电力电子等电器元件的老化、击穿,电路短路、断路或虚接,机械零件发生磨损、变形,液力系统的渗漏、堵塞,控制软件的鲁棒性、容错性不足等。不同模式故障间还可能互相干扰,如电机轴承松旷、转子变形和偏心等还会对励磁电流产生影响[2]。原车监测系统通过检测电路参数能反映电器元件或电路的某些故障信息,但往往不能准确判定故障点。特别是机械和液力系统方面的故障模式,大多没有直接反映其性能的电参数信号,需要采集振动加速度等多个相关故障特征信号,输入诊断模型处理后输出故障点和故障模式。鉴于电驱动系统故障模式和故障点的非线性和多样性,本文采用Dempster合成规则进行决策层信息融合,建立神经网络模型及专家系统产生式规则混合决策的诊断模型。
2 电驱动系统故障诊断模型理论
人工神经网络是一种具有自学习、自适应、分布存储、并行处理以及鲁棒性、容错性强等特点的数学模型,可以用来逼近任何难以用数学语言或者规则描述的非线性系统,能较好地应用于故障诊断中。径向基函数神经网络(Radial Basis Function Neural Network,以下简称RBFNN)具有局部响应特点,能避免BP神经网络训练过程易陷入局部最小等问题[3],可以得到更好的精度和运行速度,因此本文选其作为电驱动子系统故障诊断的模型。
2.1 径向基函数神经网络模型
RBFNN是由输入层、隐含层和输出层组成的三层前向神经网络,结构如图1所示。其基本原理是将在低维空间属于线性不可分问题,通过隐含层的一个核函数(径向基函数)进行非线性映射而形成一个高维特征空间,在高维空间内寻求线性可分的可能性,进而实现问题的求解。
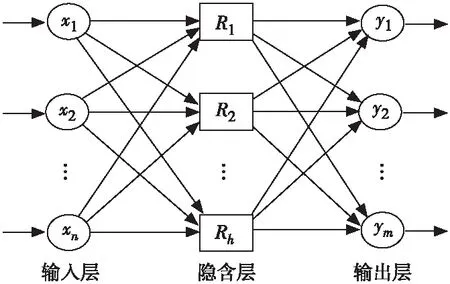
图1 RBFNN结构
隐含层中径向基函数Ri一般选择高斯函数,即
(1)
式中:输入样本向量X=[x1,x2,…,xn];Ci是隐含层节点的中心;σi是第i个基函数的宽度。
RBFNN的输出为:
(2)
式中:wi是隐含层节点和输出节点的连接权值;b0是常数;h是中心数量。
RBFNN作为智能故障判断方法,首先需由若干组样本数据(故障特征值)作为输入值进行网络训练,故障分类就是RBFNN的输出值。训练后得到的RBFNN还需通过非训练组的样本数据进行验证,以检验其故障识别的能力。
2.2 D-S证据理论的Dempster合成规则
在实际故障诊断过程中,当目标子系统较复杂时,单个神经网络模型也会存在诊断结果“不确定”或“不知道”等问题,往往不能釆用单一故障症状信息反映其实际状态,只有从各种不同方面获得的多维数据和特征才能进行更准确的诊断,而且不同的模型输出也需要进行比较和归纳的融合。D-S证据理论以其较强的不确定信息的融合处理能力,广泛应用在目标决策、状态监测和故障诊断等领域,其重要概念之一是Dempster证据合成规则。
设有识别框架
Ω={A1,A2,…,AN}
其中N为焦元的个数,有n个证据进行组合,证据集E={E1,E2,…,En},各证据对应的基本信任分配函数为m1,m2,…,mn,mi分配给Ω中焦元基本可信度mi(Aj),则Dempster证据合成规则为[4-5]:

(3)
其中k是冲突系数,表示某个证据与证据集中的其他证据的冲突程度。而
(4)
k较大时,表明该证据存在某种程度奇异,可信度应较低,对最终合成结果的影响较大;反之,该证据可信度较高,对最终合成结果影响较小[5]。
2.3 专家系统的产生式规则
产生式规则是专家系统知识表示的一种方法,它具有一般性,易于被领域专家理解,表示知识准确灵活,能充分表达领域相关的推理规则和行为。尤其在求解问题数据不全时,可用来模拟和解释大量的计算或求解过程,实现专家系统的符号推理[6]。
产生式规则表示法基本形式是A→B或IF A THEN B,其中,A是产生式规则的前提,用于指出该产生式规则是否可用的条件;B是一组结论或操作,用于指出当前提A所指示的条件被满足时,应该得出的结论或应该执行的操作。
3 诊断系统模型的建立与仿真
3.1 诊断系统模型的建立
为避免汽车电驱动系统诊断模型采用单个人工神经网络结构过于复杂无法收敛的问题,构建如图2所示的并行RBF子神经网络诊断模型,将整个故障特征参数空间分解为若干个子特征参数空间,分别输入相应的RBF子神经网络,其输出结果再与专家系统结果通过D-S理论的Dempster合成规则进行决策层信息融合。

图2 电驱动系统诊断模型
采用模块化的子神经网络模型具有较简单的结构,而且各个子网络模型互不影响,当有新的故障模式增加时,只需增加新的子神经网络,而不会影响原有子网络[7]。对于能采集故障特征参数信号及其训练数据充足的子系统采用模块化的神经网络模型,其余不具备神经网络训练条件的子系统则采用专家系统产生式规则,在神经网络模型和专家系统规则间建立一种协同决策关系。
在汽车电驱动系统出现的故障中,电源电压及逆变器IGBT异常、电机及逆变器温度过高等故障可通过诊断系统的电源及逆变器RBFNN和散热系统RBFNN进行识别。驱动电机及变速器的RBFNN则对电机的输入电流和电压进行监测,以识别定子绕组和转子的电磁故障。
当电机出现轴承损坏、转子偏心、卡滞等机械故障时,工业应用中一般可外接加速度传感器测得振动信号,再通过小波包能量分析等方法提取故障特征值进行诊断[2]。鉴于汽车的结构和运行状况复杂,振动检测信号易受外界干扰,所以先在专家系统中利用故障树及层次分析法等模型定位故障点及估计权值[8-10],建立相应规则和推理逻辑,再将其输出的故障信息与RBFNN的输出信息利用D-S证据理论进行决策层的信息融合。为避免可能出现的证据冲突悖论,在神经网络诊断模块输出后再进一步和专家系统的产生式规则交互融合,最后输出诊断结果。
3.2 电机RBFNN的训练和测试
如何选取神经网络的训练样本,将直接影响到故障诊断的能力和网络的泛化能力。在汽车电机及控制器开放协议的情况下,可以直接从中获取部分电机及控制器状态信息及故障情况[11];否则可从外接传感器进行信号采集,再对信号进行故障特征值提取处理。由于傅里叶变换存在窗口不能随频率变化等缺点,而小波变换是利用小波基对时变信号进行分解的一种信号处理方法,其可调窗口特性与信号的频率变化相适应,是比较理想的分析工具[12-14]。同步驱动电机的诊断可先提取定子电流基波分量的幅值,再通过小波变换提取特征向量。
由于工程实际中较难获得各种故障特征数据,因此利用Matlab的Simulink搭建永磁同步电机仿真模型,提取主要故障的特征参数来进行RBFNN的训练。主要方法是将在仿真正常和发生故障时分别采集到的n个(本文为1 001个)电流基波分量采样点存为单独的数组,应用小波分析工具箱wavedec函数对各组信号进行5层小波分解,小波基函数选用db6。再将5组高频系数分别进行重构得出5组数据,取出每组数据最具代表性的第一个数便形成了一组故障特征向量[15]。为便于对比分析,本文利用文献[15]的同步电机相电流故障特征样本数据输入电机RBFNN进行训练和测试,输出测试结果见表1。表1中Q0代表无故障,Q1指相间短路,Q2指单相接地,Q3指转子失磁等故障类型。训练步长曲线如图3(a)所示,可见该RBFNN只需9步即达到目标误差值,而文献[15]采用的Elman网络训练一般需166步左右才能稳定。测试误差如图3(b)所示,其中第4组(表中第4行)“失磁故障”测试数据误差最大,但其值仅在-0.14以内,表明模型测试效果较佳。

表1 RBFNN模型期望与实际输出m (Qi)测试结果
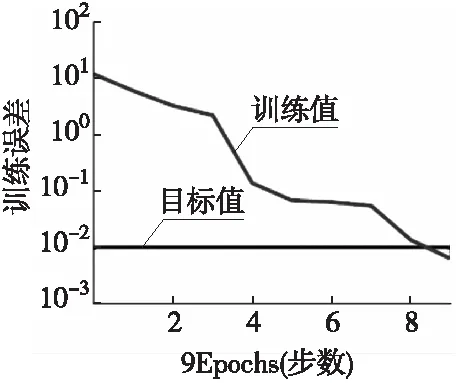
(a)RBFNN训练步长曲线

(b)RBFNN测试误差曲线
图3 RBFNN测试结果分析
3.3 诊断的决策层融合
电机和变速器RBFNN子模型的诊断输出主要用于确定电机励磁线圈及相关电路短路或断路、转子失磁等故障,但电机轴承损坏和转子偏心振动等机械故障需采集和分析振动信号后与层次分析诊断模型结果进行信息融合。如表2所示,m1(Ai)是模拟电机相关故障,通过同步电机RBFNN得到的故障模式输出的信度值;m2(Ai)是层次分析法模型得到的相关故障模式的信度值;m12(Ai)是信息融合后的输出信度值。A1,…,A4分别指定子绕组短路、断路、转子失磁、电机轴承损坏等故障。
考虑基于D-S证据理论的故障决策遵循的规则:判定故障原因应具有最大的信度函数值,并要大于某一阈值,此处取0.23;判定故障原因和其他类型的信度函数值之差要大于某一门限值,此处可取0.10。在m1(Ai)中,因为原同步电机RBFNN没有直接输出故障信度函数值,为避免证据高度冲突产生决策融合悖论,当m1(A1)~m1(A3)的信度值均低于某一阈值时(此处为0.23),可设定m1的A4信度函数值即m1(A4)为0.2[16]。
根据式(4)得:
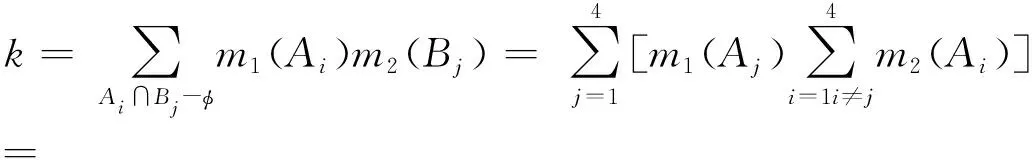
将k代入式(3)可得融合后的m1(A1)信度值:
m12(A1)=∑[m1(Ai)m2(Aj)]/(1-k)=
m1(A1)m2(A1)/(1-k)=0.010 3
同理可计算出其他焦元融合后的信度值,结果见表2中m12(Ai)。
由表2可知,经过D-S规则融合计算后输出的电机轴承故障A4的信度函数值m12(A4)最大,且高于判定阈值0.23。所以轴承故障可判定为电机故障原因。冲突系数k为0.408 3,表明证据体m1(Ai)和证据体m2(Ai)的冲突程度不高,引起冲突悖论机会少,结果可信度较高。原电机RBFNN计算结果m1(Ai)中,虽然A3的信度值较高,但未达到阈值,所以输出为不确定,与层次模型输出结果m2(Ai)融合后,输出结果中最大值为m12(A4),即轴承故障,与所设故障类型吻合,避免了原RBFNN输出m1(A3)导致的A3类型故障这一错误结论。
再进一步分析,在整个电驱动系统的故障诊断模型中,对于某一故障现象,有可能一个或数个子系统RBFNN模块都输出故障类型,此时应根据各个RBFNN的输出信息,结合专家系统的专家知识(产生式规则)对各故障类型进行权值排序和判定,最后输出诊断结果,这样可大大提高专家系统推理机的正反向推理速度和输出结果精度。
4 结束语
本文提出了以模块化的RBFNN诊断模型与专家系统的产生式规则进行混合决策,构建车辆电驱动系统的综合故障诊断系统,其中电机及变速器RBFNN与层次分析法模型先进行决策级融合,提高了电机及变速器机械和电路方面故障诊断的准确性。
