基于模型预测的智能客车路径跟踪控制研究
2020-04-25陈振国王光庭徐海柱
陈振国, 张 鲁, 王光庭, 徐海柱
(中通客车控股股份有限公司, 山东 聊城 252000)
路径跟踪控制是自动驾驶汽车的关键技术之一[1],近年来,许多学者对此进行了研究,提出了很多控制方法:PID控制[2]、模糊控制[3]以及滑模控制[4],取得了重大进展。然而这些研究工作多集中在乘用车方面,与智能客车相关的研究较少。本文提出针对智能大客车的路径跟踪控制器,其模型预测控制鲁棒性较强,能预测车辆动力学状态,并在各种约束下优化多种控制目标[5],已被用于电子稳定控制[6]、自适应巡航控制等多种智能驾驶技术中。
1 车辆路径跟踪动力学模型
研究对象为某10 m智能客车。简化的车辆动力学模型[7-8]如图1所示,建立平面坐标系xoy,可得到车辆相关运动方程为:
(1)
式中:Vx、Vy分别为车辆质心速度在x、y方向的分量;δ为前轮转角;β是车辆质心侧偏角;αf、αr分别是车辆前、后轮侧偏角;φ是车辆横摆角速度;lf、lr分别为车辆重心到前轴、后轴的距离;Iz是绕车辆重心轴线的转动惯量。
式(1)中前、后轮侧向力Fyf、Fyr的简化计算式分别为:
(2)
式中:k1、k2分别为车辆前、后轮的侧偏刚度。

图1 车辆动力学模型
车辆运动速度转化到地球绝对坐标系中的方程如下:
VY=Vxsinγ+Vycosγ,VX=Vxcosγ-Vysinγ
(3)
式中:γ是车辆坐标系与地球坐标系的夹角;VX、VY分别是车辆在地球绝对坐标系中的横向、纵向速度。
通过车载高精度定位系统测量出车辆所在位置的经度、纬度、航向角,通过墨卡托坐标投影方法[9]转化为运动平面坐标系中的平面坐标。此外,通过式(4)计算预瞄点偏差的距离ey,p、角度eφ,p的导数:
(4)
式中:Dp为预瞄距离(即驾驶员模型中,驾驶员距离预瞄点P的纵向距离);ρp为期望路径在预瞄点处的曲率。
由上述车辆动力学模型与预瞄偏差公式,得出车辆系统的状态空间:
(5)
车辆系统的状态方程为:
X=AX+BU,Y=CX
(6)
式中:X是系统的状态矩阵;U是前轮转角δ的控制矩阵;A、B、C是系统的系数矩阵:

其中,S表示路程[7]。
2 基于模型预测控制的路径跟踪
模型预测控制是根据未来的采样时间预测未来一段时间系统的状态,并求解出最优控制量。首先使用欧拉法通过泰勒展开将连续时间系统的模型转换为离散时间系统的模型来构建控制器[10],即上述式(6)使用欧拉法通过泰勒展开可得车辆系统的离散方程:
Δx(k+1)=AdΔx(k)+BuΔu(k)+N1Δe1(k)+N2Δe2(k)
yc(k)=CcΔx(k)+yc(k-1)
(7)
其中,
(8)
(9)
本文的模型预测控制器选择的预测时域p=2,控制时域m=2,根据式(7)可以预测未来p步的系统输出为[11]:
Yp=SxΔX(k)+IYd(k)+SuΔU(k)+Sd1ΔE1(k)+Sd2ΔE2(k)
(10)

(11)
(12)
下面需要求解优化问题,目标函数定义为:
(13)
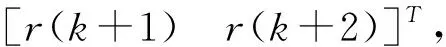
umin(k+i)≤u(k+i)≤umax(k+i)
Δumin(k+i)≤Δu(k+i)≤Δumax(k+i)
(14)
i=0,…,m-1
由于存在上述控制输出以及控制输入的约束条件,需要将问题转化为二次规划问题(QP)进行数值求解。QP问题中目标函数的标准形式是J=zTHz-gTz。将式(13)展开并定义:
Ep(k)=R(k+1)-SxΔx(k)-
Iyc(k)-Sd1Δe1(k)-Sd2Δe2(k)
(15)
则目标函数变为:
J=ΔU(k)THΔU(k)-G(k)TΔU(k)
(16)
式中:
(17)
QP问题中约束的标准形式为Cz≥b,故将约束方程(14)简化为如下形式:
(18)
(19)
式中:
(20)
令:
(21)
(22)
即可得到标准形式的约束方程。求解这个QP问题就可以得到所需的控制输入量。
通过对控制器控制方法的解析及推导可以得出,在输入量满足公式(22)要求的情况下,结合车辆控制模型即可实现对车辆的控制。
根据计算得到的输入量有跟踪路径的经纬度、车辆当前位置经纬度、航向角、本车速度(VX和VY)、预瞄距离等信息,依照第1部分搭建的车辆模型,即可实现对自动驾驶车辆的行驶控制,从而实现车辆的自动驾驶。其中预瞄距离信息可根据速度变化而变化,如低速时可设定为3 m,当速度高时可进行线性叠加。
3 实验验证
为验证所提出的路径跟踪控制器的有效性,使用中通LCK6105GZ型智能客车进行实车道路实验,如图2所示。实验车辆搭载高精度定位导航系统、主动转向执行机构、MicroAutoBox dSPACE域控制器等硬件。其中,在域控制器中加载运行的模型预测算法,是依据第2部分所述预测模型在Matlab/Simulink中使用Matlab function 等模块搭建的;高精度定位导航系统实时更新车辆绝对坐标;主动转向执行机构控制方向盘转角,各个部件之间通过车辆总线CAN通讯。

图2 实验车辆及硬件
考虑到城市客车需要有靠站停车功能,在到达站台时,经评估认为车辆距站台的横向距离在30 cm以内比较合理。所以为满足上述要求,设定车辆距站台15 cm时,车辆才满足靠站停车的要求。
如图3(a)所示对采集到的路径跟踪期望路径和实际路径数据进行分析发现,实际路径与期望路径的偏差在15 cm以内。对图3(b)车速变化分析可知,车速变化特征可以分为4个阶段:0~22 km/h、22~17 km/h、17~9 km/h、9 km/h左右。对比分析图3可知:在速度为0~22 km/h内最大误差为8 cm;在速度为22~17 km/h内最大误差为9 cm;在速度为17~9 km/h内最大误差为8.5 cm;在速度为9 km/h左右由于道路有U型弯,最大误差达到13 cm。

(a)路径对比图

(b)速度变化图
图3 实车实验路径及速度图
图4和图5所示的横摆角速度、方向盘转角基本平滑,无突变过程。

图4 车辆横摆角速度
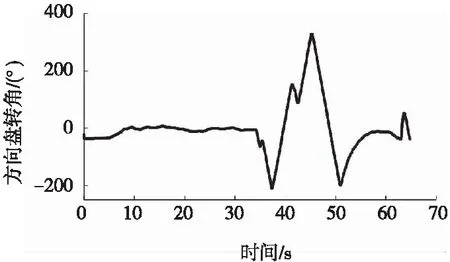
图5 路径跟踪控制器控制量(方向盘转角)
综上所述,在不同工况及车速下,车辆的横向控制误差均在可控范围内,车辆具有较强的系统鲁棒性。
4 结束语
本控制器适用于固定线路的城市客车和BRT专线,不适用于线路不固定的营运客车,目前距批量生产还有一段距离。为保证控制器的可靠性,本控制器一直处于测试中。本研究实验考虑安全因素,实验车速较低,针对高速行驶工况性能需要进一步研究和验证。
