大跨度钢结构管桁架力学性能及变形控制研究

周晨 刘洋 靳壮壮

摘要：为解决大跨度钢结构因变形失稳、应力集中造成施工难度大及节点易破坏等技术难题，本文以双龙生态公园2号游客服务中心（国际山地旅游联盟总部）大跨度钢结构工程为例，采用有限元软件Midas Gen800对三角形管桁架结构的中间榀桁杆和腹杆所受轴力进行仿真计算，研究不同载荷下管桁架结构力学性能。为验证仿真结果的可靠性，采用振弦式应变计对管桁架杆件表面温度和振动频率进行测量，计算出杆件的应变和最大应力。仿真及试验结果表明，倒三角形管桁架管端部杆件所受内力与跨中所受内力差距较大，且施加载荷、固定约束和杆件表面温度对管桁架变形有较大影响，弦杆产生最大应力为-25.52 MPa，实验结果与中间榀桁杆数值模拟所受到的应力值相仿，验证了数值模拟结果的可靠性。最后，提出管桁架结构变截面设计、施工环境温度控制和多点支撑的施工方法，有效减少施工成本，提高施工质量。

关键词：大跨度钢结构;有限元仿真;力学性能;变形控制

中图分类号：U445.556

文献标识码： A

大跨度钢结构具有结构稳定性强、自重轻、刚度大等优点，近年来广泛应用于高铁站、飞机航站楼、体育馆等建筑中[1，2]。然而，由于该结构跨度较大，各管桁架结构部件之间连接较为复杂，造成施工难度大、结构失稳或应力集中而产生结构破坏等问题，进而产生屈服倒塌事故[3-6]。因此，开展大跨度钢结构的管桁架力学性能及变性情况的研究具有重要意义。

近年来，大量学者开展了钢结构管桁架力学性能的相关研究，如天津大学姬爽[7]等人以国家海洋博物馆为例，通过有限元软件对门式管桁架及内部框架整体结构的各项力学性能进行研究。陈彦[8]等人对大跨度空间新型管析架及节点力学性能研究。张航[9]等人对伸缩拉杆对三角形析架铰接伸展臂的静力学及模态情况进行有限元仿真及数值模拟。以上研究只涉及大跨度钢结构管桁架力学性能研究，研究内容均采用有限元软件进行应力应变模拟，尚未进行试验验证，且对其变形情况进行试验研究的文献鲜有报道。

本文以双龙生态公园2号游客服务中心（国际山地旅游联盟总部）钢结构工程为例，该工程属于典型的大跨度钢结构工程，通过有限元开展其管桁架力学性能数值模拟，并采用振弦式应变计测量对管桁架表面的温度、频率进行试验数据采集，计算出管桁架的变形情况，为工程施工提供理论依据。

1工程概况

本工程为双龙生态公园2号游客服务中心（国际山地旅游联盟总部）钢结构工程，工程地点位于贵州双龙航空港经济区生态公园内，龙腾路与规划路马鞍山大道交叉口处。本工程分为南北两 侧建筑，北侧建筑建筑高度20.4 m，南侧建筑建筑高度19.5 m，其结构形式为框架钢结构，地下一层，地上四层。为提高框架柱抗弯、剪承载力，北侧建筑局部框架柱采用SRC型钢混凝土框架柱（以下简称"SRC钢柱"），屋面局部框架梁采用SRC型钢混凝土框架梁（以下简称"SRC钢梁"）。

2桁架静力学性能研究

管桁架结构作为大跨度钢结构工程中的主要结构，需满足受力稳定性好、安全性高和强度高的要求。同时，针对不同的跨度、结构性能需求，应采用合适的桁架结构，以便于安装定位方便、节省材料和施工成本。在本工程中，采用三角形桁架，该结构上弦杆受拉杆轴力，下弦杆受压杆轴力，与平面桁架和网架结构相比，增加了上弦宽度和整体长宽比，提升了整体稳定性，其结构如图2所示。

2.1三角形桁架建模

选取施工工程中的一段三角形桁架进行建模，该模型中共有下弦15格，上弦16格，并对其编号，其结构如图3所示。

采用有限元软件Midas Gen800[10，11]对三角形管桁架结构进行力学性能分析，建立其有限元模型，并将弦杆采用梁单元模拟，腹杆及系列杆采用桁架单元模拟，约束条件设定为一端固定，另一端进行铰链连接，采用下承式支承。整个三角形桁架中上弦杆长度为64 m，下弦杆长度为60 m，其編号如图3所示。在有限元中网格划分时分别选取整个桁架上下弦的一般进行网格划分，方便设置纵向变桁架。计算模型高度符合工程实际及相关理论设计经验，按照网格规范将跨度取值为1/15，并根据《钢结构设计规范》[12]GB50017-2003将上弦平面的斜腹杆与弦杆的夹角α取值为30～45°，上弦宽度设计为3.5 m。

2.2施加载荷及参数设置

在该结构的有限元模拟中载荷以恒定载荷和动载荷两种形式施加，其中恒定载荷为1.2 kN/m2，动载荷为0.4 kN/m2，，将两者进行组合，取一定的比例因子，本文中其载荷取值为q=1.32F恒+096F动。按照满应力原则，结合所选取的杆件实际尺寸，将应力比保持为0.8，压杆长细比控制值为160，拉杆长细比控制值为180，挠度限值为L/250，且相邻两个受力相同的桁架间其横截面积比小于1.8倍。

2.3结果分析

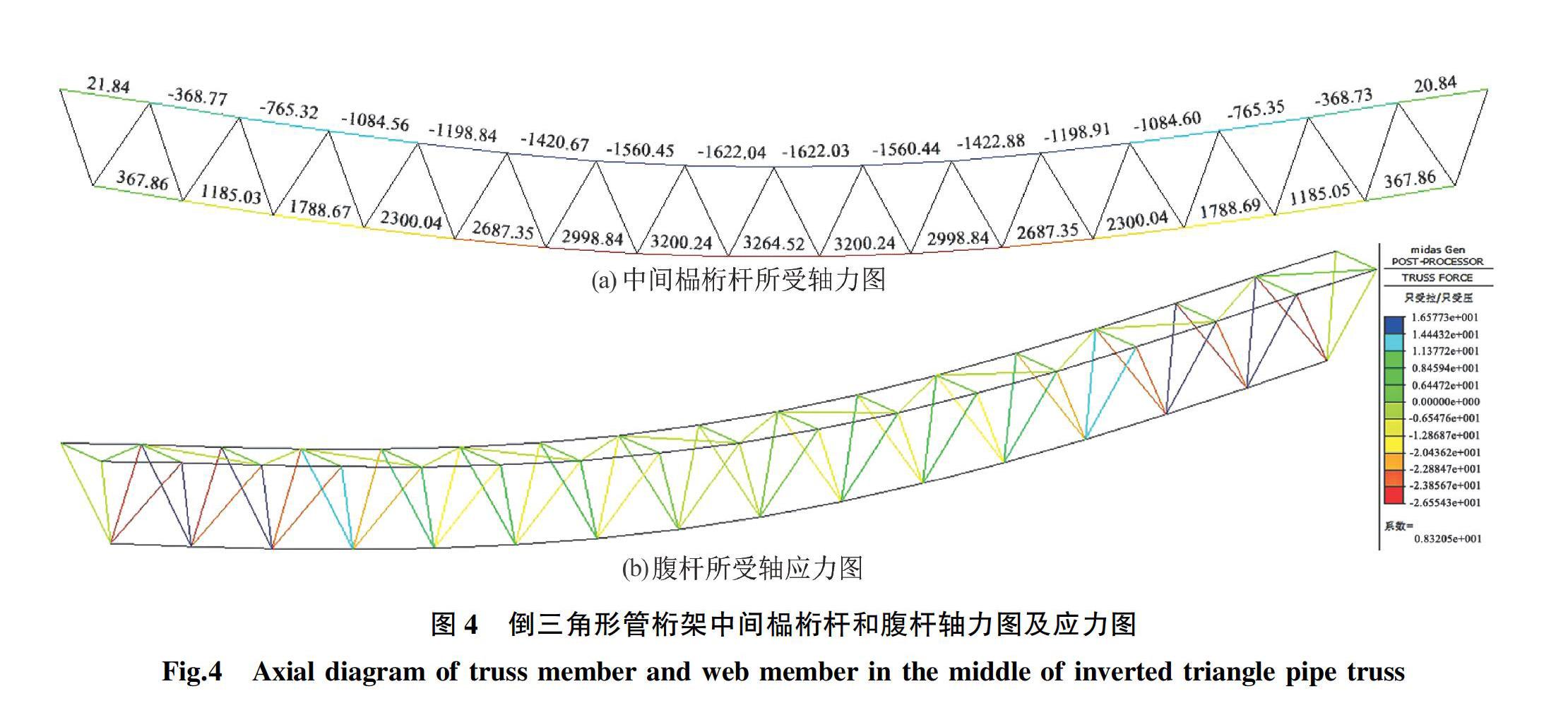
按照设置的约束条件、载荷和参数下，在Midas Gen800中进行桁架中间榀桁杆和腹杆所受轴力进行仿真，其结果如图4（a）和4（b）所示。由图4（a）可知，在给定的竖向荷载作用下，倒三角形管桁架下弦杆表现为受拉，上弦杆表现为受压，且在左右对称结构的三角形管桁架中中部受力集中，内力值较大，两端端部受力较小。由图4（b）可知，腹杆受到的最大应力σmax=-26.554 MPa，跨中应力较小，两端较大。

此外，由图4（a）可知，中间榀桁架下弦杆两边端部1/3跨度范围内杆件在给定荷载下所受内力平均值为从中间点向左右对称的1/3跨度范围内杆件受到内力平均值的57.67%;中间榀桁架上弦杆两边端部5/16跨度范围内杆件在给定荷载下所受内力平均值仅为从中间点向左右对称的5/16跨度范围内杆件受到内力平均值的48.05%。可以看出，本工程中采用的倒三角形管桁架管端部杆件所受内力与跨中所受内力差距较大，这种采用同一截面贯通整个桁架的设计方式会造成大量的材料浪费，因此，可以根据应力的大小情况，采用变截面法设计整个桁架管结构，即在满足结构强度、承载力和刚度，同时保证杆件应力比、长细比和扰度的条件下，从内力值有较大突变位置开始采用变截面设计，该方法可以减少整个工程的用钢量，减少施工成本。

3管桁架变形试验研究

为研究大跨度钢结构管桁架结构在加载前后的变形情况，本文采用振弦式应变计进行管桁架杆件的应变测量。振弦式应变计的工作原理为当构件有应力变化出现时，振弦式应变计前后端的底座将变形转化为内部钢弦的变形，进而改变弦振片的固有频率，电磁线圈对振弦进行激振可以测量得到其振动频率，该振动频率可以在对应的采集仪上读取，通过公式（1）可求得相应的应变，同时，振弦式应变计配有热敏电阻器，可测得周围温度变换，且具有温度补偿功能[13-15]。

ε=K（f2i-f20）（1）

式中，ε为测量构件的应变值，με，ε为正值时，表现为受拉，ε为负值是表现为受压;K为标定系数;f0为加载前振弦式应变计的初始振动频率，Hz;fi为加载后振弦式应变计的实测振动频率，Hz。

3.1试验方案

本次试验中数据采集部位为钢结构管桁架表面，测点分布在南楼、北楼，分别是上弦杆A、B、C、D、E，在每根弦杆上分别布置测点1（下部）和测点2（侧部）两个，同理，在下弦杆A、B、C、D、E相同位置上布置测点1和测点2，共计20个测点。测量时间从2019年7月16日至2019年7月22日，应变测量主要阶段为管桁架杆件拼装前、管桁架安装完成并施加荷载后，

在不同环境温度下按试验设计方案进行应变测量。通过前期理论分析及数值计算模拟，管弦架A作为主要承载部件，受到的载荷力及产生的应变最大，因此本文选取管弦架A的上弦杆和下弦杆作为分析对象，分别分析加载前和加载后上弦杆A和下弦杆A的表面温度变化和产生的应变情况。数据采集时，采集目标为钢结构在不同时间段不同温度下的频率变换，在通过转化求得管桁架的应变，试验现场如图5所示。

对加载前后上弦杆A和下弦杆A的数据采集中，使用的8个传感器的型号及对应的初始对应频率和标定系数见表1。

3.2结果分析

记录不同时间段下管桁架的表面温度，并将初始频率值f0及标定系数K值代入式（1）中，计算出相应的表面应变，其中加载前上下弦杆测点1和测点2的表面温度和应变如图6、7所示。

由图6、7可以看出，加载前上弦杆A的表面温度呈周期性变化，主要是由于测量周期较长，杆件表面温度随大气温度而变化，总体而言，测点1表面温度（下部）低于测点2（侧部），主要是由于侧部在阳光照射下使杆件表面温度上升。对于应变而言，加载前测点1的最大应变为-222.18με，此时杆件表面温度为38.7℃，测点2的最大应变为-320.47με，此时杆件表面温度为22.5℃，均表现为受压状态。由于上弦杆A侧部受到自身横向内应力较小，故测点2处的应变随表面温度的升高逐渐减小，而下部要承受自身重力载荷，随着温度上升，在膨胀作用下使测点1处的应变随表面温度的升高呈上升趋势。

对于加载前的下弦杆A，杆件表面温度变化趋势及原因与上弦杆相同。但下弦杆测点1的最大应变为-261.33 με，此时杆件表面温度为233℃，测点2的最大应变为-382.4με，此时杆件表面温度为39.5℃，均表现为受压状态。与上弦杆A相反，下弦杆A下侧受到自身横向内应力较小，故测点1处的应变随表面温度的升高逐渐减小，而侧部要承受自身重力载荷，随着温度上升，在膨胀作用下使测点2处的应变随表面温度的升高呈上升趋势。

由图8、9可以看出，加载后上弦杆A的表面温度也呈周期性变化，测点1表面温度（下部）低于测点2（侧部），其原因与加载前相同。对于应变而

言，加载后测点1的最大应变为-155.63με，此時杆件表面温度为21.5℃，测点2的最大应变为-116.1με，此时杆件表面温度为26.3℃，均表现为受压状态。当榀桁架两端固定施加载荷后，上弦杆A侧部受到自身横向内应力较大，故测点2处的应变随表面温度的升高逐渐增大，而下部承受自身重力载荷的影响相对于施加载荷可忽略，故随着温度上升，在膨胀作用下使测点1处的应变随表面温度的升高呈下降趋势。

对于加载前的下弦杆A，杆件表面温度变化趋势及原因与上弦杆相同。对于应变而言，加载后测点1受压的最大应变为-80.55 με，此时杆件表面温度为21.5℃，受拉最大应变为63.3  με，此时杆件表面温度为29.4℃;测点2的最大应变为-1215.25 με，此时杆件表面温度为20.9℃，均表现为受压状态。测点1同时受到拉应力和压应力，产生不同方向的应变，而测点2由于榀桁架两端固定施加载荷后，较大的载荷在机械铰链耦合作用下，会在较低温度下产较大的受压应变，并且随着温度的上升应变逐渐减小，但减小趋势并不明显。

3.3加载前后应变结果对比

加载前杆件一段固定约束，一段呈自由状态，加载后两端均固定约束，两种不同状态下杆件所受到的应力和应力状态均不相同，为能够更方便直观的将加载前后上弦杆、下弦杆上测点1和测点2的应变数据进行对比，分析不同状态下产生不同应变的原因，并验证模拟计算结果的可靠性，将采集到的应变数据进行绘图，如图10、11所示。

通过对加载前后上弦杆A和下弦杆A测点1、测点2的应变情况进行对比可以看出，加载前上弦杆A测点1、测点2处的应变均值整体高于加载后，主要原因为在没有固定约束作用下，载荷及杆件表面温度对产生的应变影响较大。同理，加载后下弦杆测点1的应变低于加载后，加载后测点2的应变远高于加载前，其原因为榀桁架两端固定施加载荷后，下弦杆A下侧在固定约束下纵向载荷较小，产生的轴向应力较小，而侧部受到自身横向内应力较大，自身重力载荷的影响相对于施加载荷可忽略不计，故产生的应变远大于加载前。

由于管桁架是鋼材料，其弹性模量E=210 GPa，由公式σ=E·ε可计算出，在上下弦杆A产生最大应变处的最大应力为-25.52 MPa（压应力），实验结果与中间榀桁杆数值模拟所受到的应力值相接近，验证了数值模拟结果的准确性。

4变形控制方案

根据数值模拟结果和实验结果可知，要保证钢结构管桁架的变形最小，可以采用以下方法：

（1）根据应力的大小情况，采用变截面法设计整个桁架管结构，即在满足结构强度、承载力和刚度，同时保证杆件应力比、长细比和扰度的条件下，从内力值有较大突变位置开始采用变截面设计。

（2）为减少上、下弦杆的应变量，采用多点支撑施工方法，可有效减少整个管桁架的应力集中，避免产生较大的形变而影响施工质量。

（3）施工时间尽量保持在适宜温度环境中，避免管桁架表面因温度过高或过低引起热胀冷缩而产生较大的应变。

5结论

本文以双龙生态公园2号游客服务中心（国际山地旅游联盟总部）大跨度钢结构工程钢为例，开展了钢结构管桁架力学性能有限元数值模拟，并采用振弦式应变计测量出管桁架的应变情况，主要得出以下结论：

（1）本工程中采用的倒三角形管桁架管端部杆件所受内力与跨中所受内力差距较大，采用同一截面贯通整个桁架的设计方式会造成大量的材料浪费，提出采用变截面法设计整个桁架管结构，可以减少整个工程的用钢量，节约施工成本。

（2）施加载荷和固定约束对管桁架变形有较大影响，可采用多点支撑施工方法，有效减少整个管桁架的应力集中，避免产生较大的形变而影响施工质量。

（3）杆件表面温度对管桁架应变有较大影响，因使施工时间尽量保持在适宜温度环境中，避免管桁架表面因温度过高或过低引起热胀冷缩而产生较大的应变。

（4）在上下弦杆A中产生最大应变处的最大应力为-25.52 MPa，实验结果与中间榀桁杆数值模拟所受到的应力值相接近，验证了数值模拟结果的准确性。

参考文献：

[1]

董超. 预应力大跨度空间钢结构的应用与展望[J].黑龙江科技信息，2014（03）：213.

[2]董石麟. 我国大跨度空间钢结构的发展与展望[J].空间结构，2000（02）：3-13.

[3]AUGENTI N， PARISI F. Buckling analysis of a long-span roof structure collapsed during construction[J]. Journal of Performance of Constructed Facilities 2013，27（1）：77一88.

[4]李德，曹平周，傅新芝，等. 江苏大剧院音乐厅钢屋盖施工模拟分析[J].建筑科学，2016，32（01）：129-134.

[5]周红波，高文杰，黄誉. 钢结构事故案例统计分析[J].钢结构，2008（06）：28-31.

[6]郭超，刘秀丽，马俊峰，等.大跨度钢结构施工跟踪模拟计算分析[J/OL].青岛理工大学学报，2019（06）：1-10[2019-12-01].http： //kns.cnki.net/kcms/detail/37.1440.N.20191128.1008.036.html.

[7]姬爽. 国家海洋博物馆门式钢管桁架结构力学性能研究[D].天津：天津大学，2014.

[8]陈彦. 大跨度空间新型管桁架及节点力学性能研究[D].天津：天津大学，2017.

[9]张航. 伸缩拉杆对三角形桁架铰接伸展臂力学性能影响研究[D].长春：吉林大学，2018.

[10]刘俊伟，韩金朋，于秀霞，等. 基于Midas软件的预制拼装管廊变形规律研究[J/OL].水利水电技术：1-7[2020-01-13].http： //kns.cnki.net/kcms/detail/11.1757.tv.20191127.1323.002.html.

[11]张海风，黄政华. 非等径法兰节点板静荷载作用下的承载力有限元分析[J].贵州大学学报（自然科学版），2015，32（06）：122-126.

[12]GB 50017-2003钢结构设计规范[S].北京：中国计划出版社，2003.

[13]张宇佳. 振弦式应变计在土木工程中应用进展[J].江西建材，2016（10）：154.

[14]李滨，钟文斌，林飞振. 振弦式应变计数学模型的比较分析[J].上海计量测试，2013，40（04）：8-11.

[15]刘杨. 振弦式传感器温度补偿研究[D].长沙：长沙理工大学，2009.

（责任编辑：于慧梅）