基于预测PI的加热炉温度控制

谭志君,胡金雪

（飞马智科信息技术股份有限公司，安徽马鞍山 243000）

引言

加热炉在工业生产中有着举足轻重的地位，由于该系统具有大惯性、大滞后、强扰动、时变等特性，所以其温度控制是一个十分复杂的过程，搭建数学模型非常困难[1]。大量的加热炉系统如果采用PID 算法则无法达到预期的效果。根据大惯性、大滞后和时变等特性我们设计出一个能够满足其控制效果的预测PI 控制器，对于加热炉温度控制意义重大。

本文提出了一种基于预测PI 的加热炉控制算法，利用预测PI 控制算法对控制对象大滞后的补偿和对模型参数要求的不精确性，通过仿真得出预测PI算法具有很好的动态特性与抗干扰能力。

1 预测PI控制算法

传统的PID 控制算法在整定控制器的参数时比较繁琐，同时在处理工业现场的大惯性、大滞后过程时对模型不匹配比较敏感，稳定性不高，鲁棒性也不理想。

预测控制是在20 世纪70 年代后期产生的。它的主要特点有：滚动优化的时变性，预测模型的多样性，在线校正的鲁棒性[2-5]，它是一种基于模型、滚动优化并且结合反馈校正的先进控制算法。

1992 年由Hagglund 第一次提出预测PI 控制算法这个概念，该算法由两部分组成：PI 部分和预测部分，一共有5 个参数，其中可调参数仅有3 个。控制器的传递函数可表示为：

在公式中，λ是微分算子，λ越小，闭环响应速度越快，反之则会越慢。E(s)和U(s)为该控制器的输入和输出，（1）式右边第一项为PI 控制器，第二项为预测控制器。在控制器参数设置中，kp为过程对象的增益，T 为过程对象的主导时间常数，τ 为过程对象的滞后时间。由该公式结构可以看出预测PI 控制算法不仅具有PI 算法的功能，还有预测的功能，非常适合大惯性、大滞后过程对象的控制，并且控制简单，可调参数少[6]。

2 预测PI控制器的工作原理

考虑下面的单位负反馈系统,见图1。

图1 单位负反馈系统结构图

其中控制器与被控对象的传递函数为Gc(s)和Gp(s)，得出闭环传递函数为：

通过变换得出Gc(s)的传递函数为：

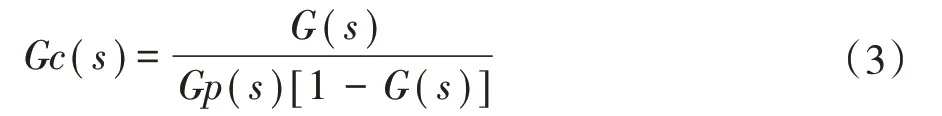
假设被控过程对象的数学模型为：

同时，假定所期望的闭环传递函数为：

（5）式中，λ是一个可调参数，它主要影响系统闭环响应的速度。若λ＜1 时,则开环系统比闭环系统响应慢；若λ＞1 时,则开环系统比闭环系统响应快[7]。

然后将等式（4）、（5）代入等式（3）以获得控制器的传递函数：

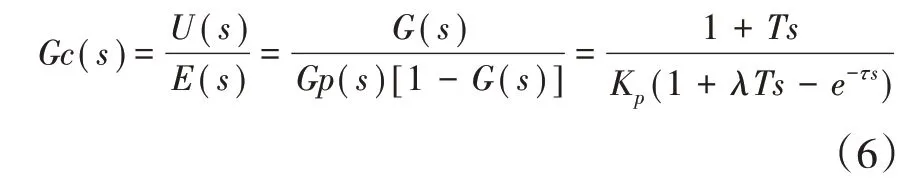
从而得到：

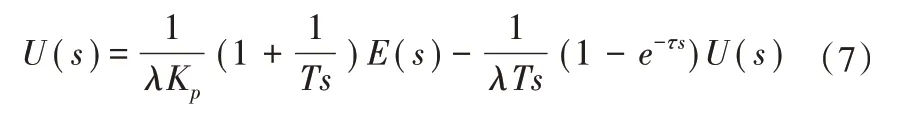
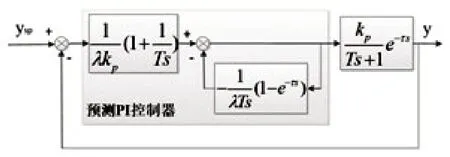
图2 预测PI控制结构图

3 仿真及结果分析

我们必须先对其安全性和可行性进行分析，然后进行大量的仿真实验，再将控制方法应用于现场生产。因此很有必要先在实验室进行模拟仿真。为了验证该控制系统的有效性，我们在Matlab 中的Simulink 工具包中模拟了控制系统，最后对控制方案作出分析与评价[9]。

由于加热炉是一个十分复杂的被控过程对象[10]，目前还没有与之匹配的数学模型。为了方便控制方法的研究，我们根据加热炉大惯性、大滞后的特点，将加热炉简化为一个一阶惯性纯滞后环节，传递函数为：

为了检验预测PI 控制算法的各种性能，我们选取了如式（8）的具有一阶惯性纯滞后模型进行仿真试验。并与PID算法进行比较。对从系统的动态特性、跟踪特性、抗干扰特性以及鲁棒性这几个方面进行分析。

假设有如下一阶惯性滞后系统G(s)=从该系统的传递函数中得出其时间常数为10，滞后时间为14，由于其滞后时间与时间常数之比大于1，因此该过程对象是一个大滞后对象。然后根据被控过程对象各项参数对预测PI 控制器的参数进行整定，以及对PID 控制器用Cohen-Coon法和Ziegler-Nichols 经验公式法进行参数整定。当阶跃为300的输出干扰在400 s的时候加上，输出响应如图3所示。

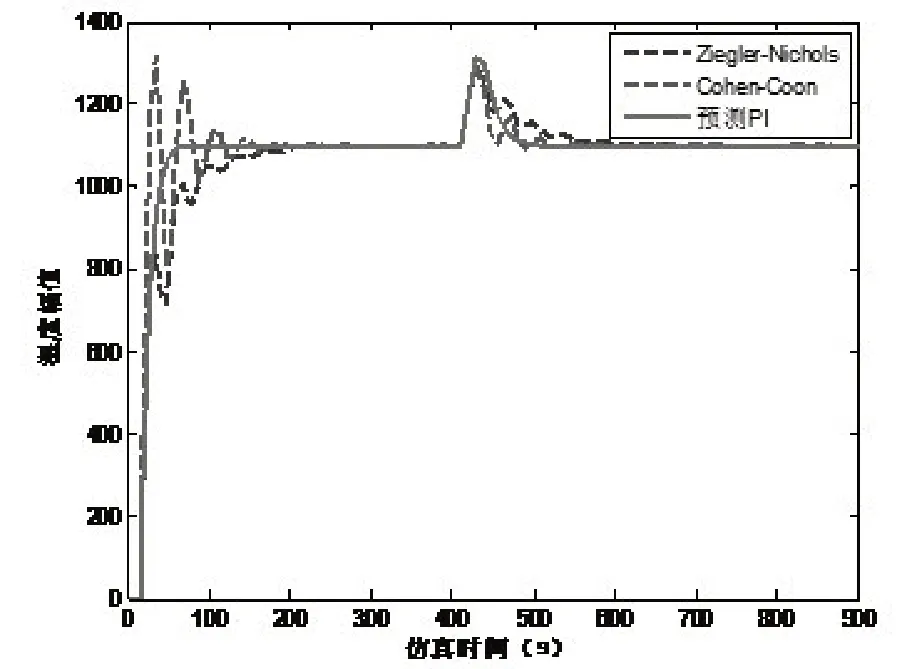
图3 PID和预测PI的仿真效果对比

从输出响应曲线上可以看出，Ziegler-Nichols法具有一定的振荡，并且上升时间也比较慢；而Cohen-Coon 法达到稳态时间较长且有较大的超调。在改用预测PI 算法后没有了超调和振荡且上升时间缩短很多。在400 s有阶跃为300的扰动的时候，预测PI控制算法比Ziegler-Nichols 法和Cohen-Coon法恢复到稳定状态的时间短，可以得出预测PI 控制算法的跟踪性能和抗扰动能力比PID算法好。由此仿真可以得出预测PI 控制算法系统无超调，跟踪速度快而且抗干扰能力好。

当跟踪到初始设定值后，更改最初的设定值。将系统的设定值从原先的1100改为1400，过一段时间后系统能够快速跟踪到新的设定值。如图4 所示。

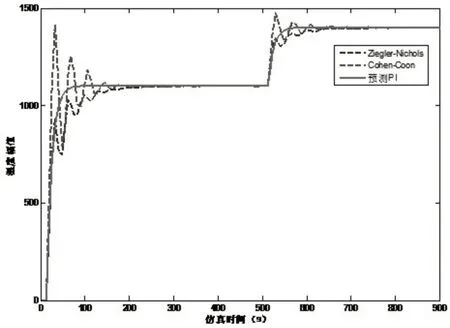
图4 设定值改变后两种控制的仿真效果对比

从图4 中可以看出，当系统的设定值改变以后用Cohen-Coon 法的系统不能快速跟踪系统的设定值并且具有一定的振荡。用Ziegler-Nichols 法虽然没有振荡，但是它的快速跟踪能力也不是很理想。而在选用预测PI 控制后，系统在没有振荡产生的情况下能更快的响应新的设定值，说明其具有较好的快速跟踪性能。

通过改变被控过程对象的参数,而让各个控制器的参数不变,观察其输出响应来检验这几种控制算法的鲁棒性。把时间常数从10 调整到12，即，或者将滞后时间从14 调整到18，即但对预测PI 和PID 控制器的参数不作改变，得到的结果如图5和图6所示。

图5 时间常数失配下的输出响应

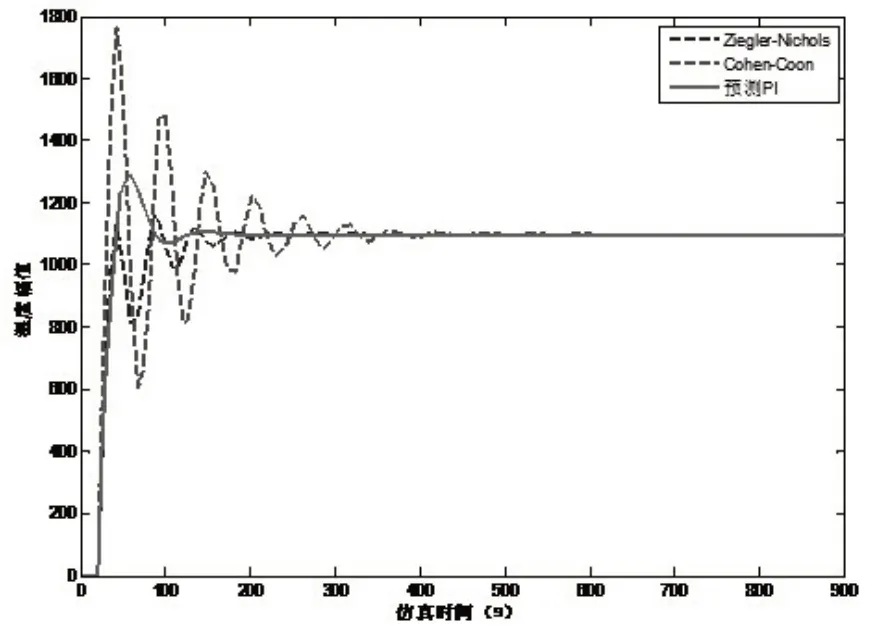
图6 滞后时间失配下的输出响应

从图5 和图6 中可以看出，在滞后时间失配下，PID控制下的Cohen-Coon法系统有较大的超调和振荡。虽然Ziegler-Nichols 法没有超调和振荡但是其达到稳态用时较长。再来看预测PI 控制在滞后时间或时间常数的模型失配的情况下仍具有较好的控制性能，受模型失配的影响较小，由此可以看出系统的鲁棒性非常好。

4 结论

本文针对加热炉这种大惯性、大滞后，强干扰，时变的温度控制过程对象，提出了基于预测PI 的控制策略。并在理论上进行了阐述，同时将基于预测PI 的控制系统进行仿真得到了良好的响应曲线，通过仿真可以得知其比传统的 PID 算法在性能上不仅快速响应能力有所提高，而且抗干扰能力也得到了加强。