基于风电塔架结构的智能材料耗能阻尼器研究

阎石，牛健,2

（1.沈阳建筑大学 土木工程学院；2.大连理工大学 建设工程学部）

1 引言

风电塔架结构作为风力发电机的主要支撑结构，除了承受自身运转的振动外还要受到外部强风、地震和海浪等环境荷载的影响，如何智能、高效、经济地降低风电塔架结构的振动成为工程结构减振控制中一个重要问题[1]。作为典型的智能材料，形状记忆合金（shape memory alloys，简称SMAs）以其超弹性、高阻尼、高恢复力等特点，可用于减小高柔塔架结构的减振。结合风电塔架结构的振动特点，根据其内部有限的空间，有针对性地设计一种形状记忆合金-悬吊质量摆减振系统（Shape Memory Alloy-Suspension Mass Pendulum Damping System，简称SMA-SMPD 系统），并通过超弹性SMA 丝的拉伸来耗散振动能量并增强复位作用，以达到对高柔塔架结构振动有效控制的目的，具有智能、高效、实用等特点。

2 SMA-SMPD 系统构造设计

2.1 SMA-SMPD 系统整体设计

将直线型SMA 耗能减震装置布置在对角线方向相对位移较大的框架结构中，证明了该装置可有效控制框架结构整体位移[2]。风电塔架结构具有高柔且截面轴对称、中心对称等特点，改进直线型SMA 耗能减震装置，设计一种适合风电塔架结构的SMA-SMPD 系统，如图1 所示。该减振系统布置在风电塔架内部，整体呈圆形，主要由1 个环形（或圆盘状）的质量振子、8 个与水平刚性杆（防屈曲杆）相连的SMA 阻尼器和8根悬吊钢索等构成，悬吊布置在风电塔架结构顶部，安装在顶部的附加钢承重结构上。

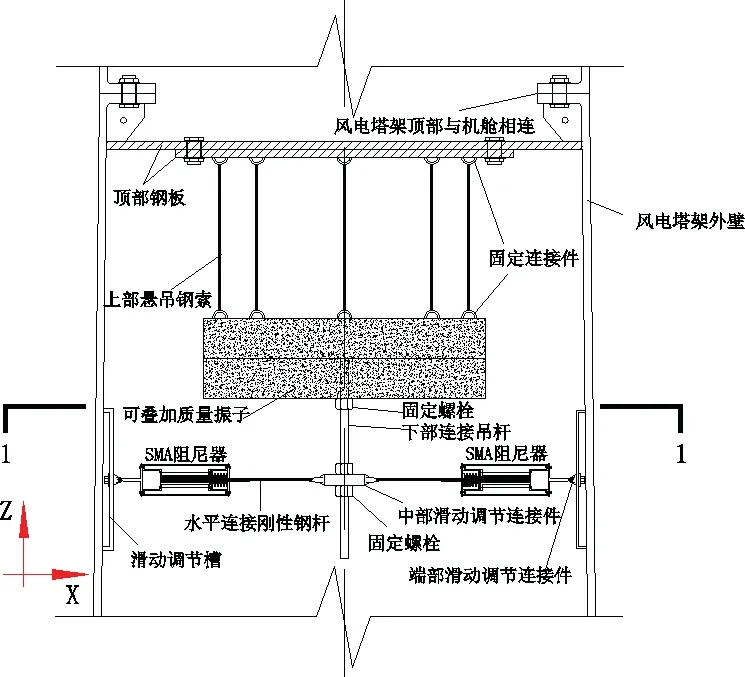
图1 SMA-SMPD 系统立面示意图

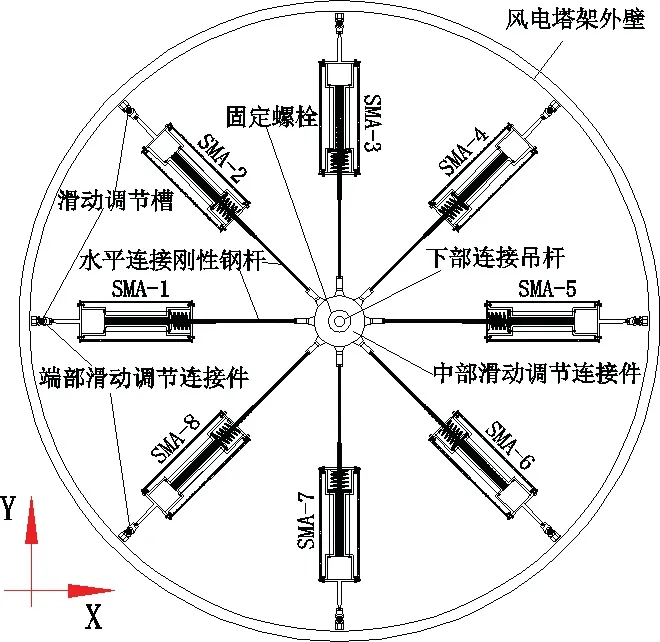
图2 SMA-SMPD 系统平面布置图

利用SMA 丝的超弹性特性并结合SMPD 减振原理，将SMA 阻尼器与一段刚性钢杆相连，假设钢杆刚度远大于SMA 阻尼器刚度，将风电塔架结构在振动过程中产生的位移等效集中到SMA 阻尼器上。SMA 阻尼器一端通过端部滑动调节连接件与滑动调节槽相连，滑动调节槽固定在塔架结构内壁，即SMA 阻尼器一端与塔架内壁相连；另一端的刚性钢杆通过中部滑动调节连接件与质量振子下部连接吊杆相连，即与质量振子相连，在平面内均匀布置8 个与刚性钢杆相连的SMA 阻尼器，SMA-SMPD 系统中SMA 阻尼器布置如图2 所示。

为了使SMA-SMPD 系统设置在不同高度、不同质量的塔架结构中，并适用于不同频率的多种振动控制中，而进行了细部优化设计。通过设置下部连接吊杆可叠加多个质量振子，用固定螺栓将叠加的质量振子固定为一个整体质量块，其重量也可根据需要选择不同密度的材料，目的是为了增大系统对主结构质量比的调整范围；同时设置下部连接吊杆还释放了质量振子水平位置周边的有效空间，使SMA 阻尼器和刚性钢杆布置更加灵活多变。设置滑动调节槽、端部滑动调节连接件、中部滑动调节连接件以及固定螺栓，可调整SMA 与刚性钢杆相连的阻尼器在塔架内部的水平高度位置，端部和中部调节连接件同时可调整，确保8 根SMA 阻尼器和刚性钢杆在同一水平面内。上部悬吊钢索的长度设置为可调节，吊点到质量振子质心的距离是SMPD 的有效摆长，目的是为了使SMPD 的频率可调，因此SMPD 长度是影响SMA-SMPD 系统频率的重要 因素。

以上的细部优化设计，实现了SMASMPD 系统质量比、频率比可调节的想法，解决大部分TMD 质量和频率无法调整的难题，使SMA-SMPD 系统适用于不同高度、不同质量、不同频率的风电塔架结构，同时适用于不同激励的减振控制。

2.2 SMA 阻尼器细部构造

SMA 阻尼器整体设计呈筒状结构，详细构造如图3 所示，由SMA 丝、预压弹簧、推拉杆、内导筒、外筒、弹簧挡板、外挡板等主要部件组成。

弹簧挡板为圆形钢板且中间带孔洞，直径略小于外筒内径，安装在右侧外挡板与内导筒之间的空腔内。预压弹簧安装在弹簧挡板和右侧外挡板之间的空腔内，外挡板通过固定螺栓与外筒固定成整体。内导筒内直径设计略大于推拉杆内直径，在推拉杆左右移动时起导向作用，内导筒与外筒之间形成的狭长空腔可布置SMA 丝，该腔对SMA 丝还具有保护作用。SMA 丝穿过内导筒与外筒的空腔间，布置于内导筒外壁与弹簧挡板之间，两端分别用固定夹具螺钉固定。推拉杆在弹簧挡板处有变径处理，受拉向右运动时可带动弹簧挡板一起向右移动，压缩弹簧的同时拉伸SMA 丝。左侧外挡板与外筒之间形成的空腔是推拉杆受压左移时的预留空间，左侧连接件与固定在塔架内壁的端部连接件相连，右侧连接件通过刚性钢杆与中间连接件 相连。

3 SMA-SMPD 系统工作原理及力学特性

3.1 SMA-SMPD 系统工作原理

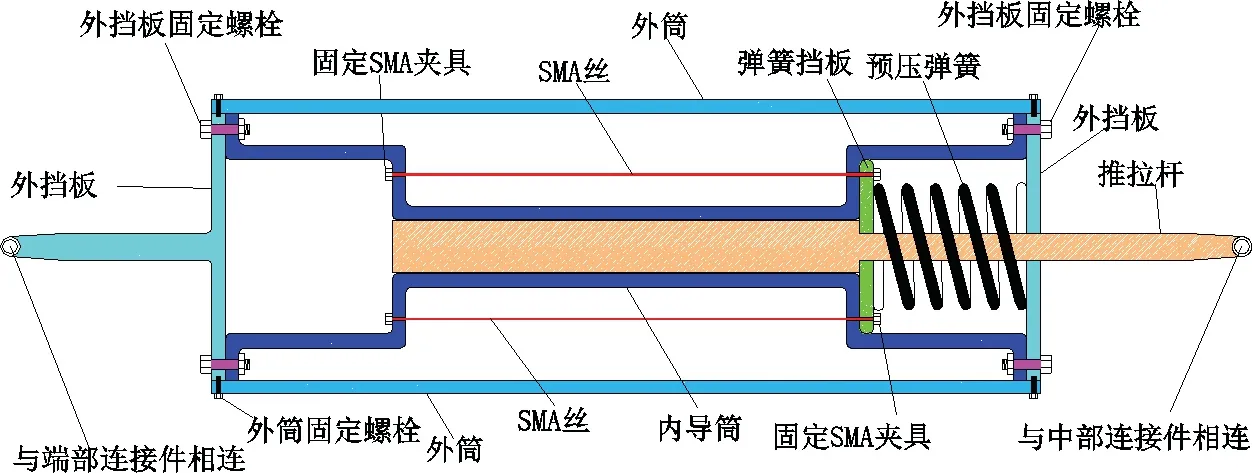
图3 SMA 阻尼器构造示意图

当风电塔架结构受到外部激励而产生振动时，带动质量振子做往复摆动，连带SMA 阻尼器运动。当悬吊质量振子向右侧运动时，下部吊杆通过连接钢体带动左侧SMA 阻尼器推拉杆向右运动，使左侧SMA 阻尼器（SMA-1，2，8）中的SMA 丝组被拉伸而进入工作状态，同时右侧SMA 阻尼器（SMA-4，5，6）推拉杆被压缩但未处于工作状态，SMA-3和7 出力较小可忽略，阻尼器代号如2所示。当悬吊质量振子由右侧最大位移位置恢复到平衡位置（x=0）时，左侧阻尼器中受拉的SMA 丝回到初始状态，悬吊质量振子由平衡位置摆向右侧最大位置后再摆回到平衡位置这个过程，迫使左侧SMA 阻尼器及其中SMA 丝组正好经历了一次加载-卸载的循环耗能过程，左侧阻尼器发挥了对风电塔架结构整体的耗能减振作用。悬吊质量振子的惯性力又通过连接刚性钢杆和SMA 阻尼器反作用到风电塔架结构上，对风电塔架主结构的振动产生抑制作用，使风电塔架结构整体的振动得到衰减。这个力在风电塔架空间平面内是三个SMA 阻尼器的合力，平面受力分析如图4 所示。假定：第一，SMA-3 和SMA-7 阻尼器不参与工作，即忽略互相垂直方向SMA阻尼器的影响；第二，当质量摆向右摆动且经过平衡点后，SMA-4，5，6 三个阻尼器受压也不参与工作。因此，只有SMA-1，2，8 三个阻尼器处于被拉伸状态而参与工作，合力如式（1）所示。

式中，FR为SMA-SMPD系统的合力；R1，R2和R8分别为阻尼器SMA-1，2 和8 提供的阻尼力。

同理，当悬吊质量振子向左侧摆动到最大位置后再回到平衡这一过程中，右侧SMA 阻尼器中的SMA 丝组同样经历了一次由加载-卸载的循环耗能过程，耗能减震原理与右摆时一致。两侧SMA阻尼器在SMPD 往复摆动过程中交替参与耗能减振工作，因此，SMA-SMPD 系统在风电塔架结构振动过程中始终处于耗能减震工作状态中。

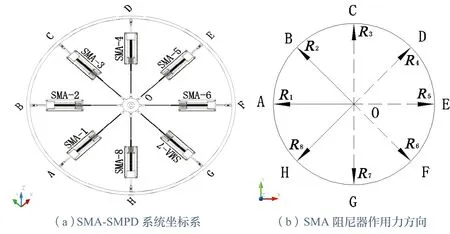
图4 SMA-SMPD 系统平面受力分析图

图5 SMA 阻尼器工作原理图

SMA 阻尼器为拉伸耗能型阻尼器，分为耗能和复位两部分。将SMA 丝组的拉伸循环视为耗能部分，将弹簧的压缩视为复位部分。SMA 阻尼器特点是整体可以受压，但SMA 丝始终不受压，且受压时没有耗能能力，拉伸耗能装置的工作原理如图5 所示。SMA 阻尼器自然状态下长度为L，其中SMA 丝长度为L0，弹簧长度为L1，如图5 所示。当SMA 阻尼器两端受拉产生位移ΔL0时，阻尼器内部总位移都将集中于右端的推拉杆上，推拉杆会向右运动，直接带动弹簧挡板向右运动，弹簧挡板拉伸一端固定其表面的SMA 丝组，使其产生位移，同时弹簧挡板又压缩右侧的预压弹簧也产生相应大小的位移，位移值均为ΔL0，如图5（a）所示。SMA 丝受拉而耗散能量，弹簧受压而具有恢复力，使得SMA阻尼器在耗能的同时达到自复位的功能。当SMA 阻尼器两端受压产生位移ΔX时，只有推拉杆向内移动产生，产生位移ΔX，但SMA 丝并未受压或松弛，如图5 (b)所示。

3.2 SMA-SMPD 系统力学性能

所设计的SMA-SMPD 系统的控制力由8 个SMA 阻尼器共同提供，而每个SMA 阻尼器的SMA 丝组和预压弹簧并联工作，共同提供该阻尼器的控制力。单个SMA 阻尼器的控制力为

式中，SMAF 为SMA 丝组提供的控制力，具有耗能作用；TF 为预压弹簧提供的控制力，具有复位作用。

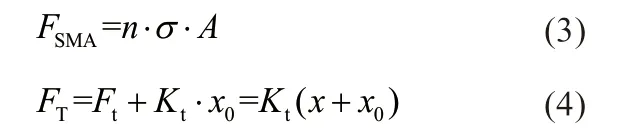
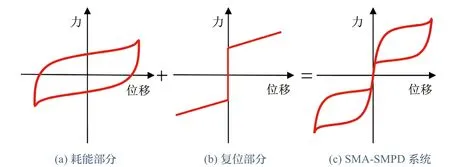
图6 SMA-SMPD 系统滞回曲线

式中，n 为SMA 阻尼器中SMA 丝的根数，σ 为SMA 丝应力，A 为单根SMA 丝的截面面积；Ft为弹簧预压力，Kt为弹簧刚度，x0为弹簧压缩的位移。

SMA-SMPD 系统 中 有8 个SMA 阻尼器，其中每两个中心对称的阻尼器组成一对并交替工作。以位于x 轴上的一对SMA 阻尼器为例进行说明，其控制力由SMA-1 和SMA-5 交替提供的，滞回曲线由耗能部分(图6(a))和复位部分(图6(b))的力-位移关系曲线叠加而成，表现为双旗形状，如图6(c)所示，其中第一象限曲线代表SMA-1 工作，地三象限曲线代表SMA-5 工作。

1967 年Bouc 提出了能够模拟结构滞回现象的一种数学形式简单模型[3]。1976 年，Wen 等人改进了此模型，使其系统化地表示各种滞回线的滞回非线性模型，即Bouc-Wen 模型[4]。Bouc-Wen模型表达式如式（5）和（6）所示，其中含有滞回恢复力和位移的一阶非线性微分方程以及一系列不确定的控制参数，力学模型如图7 所示，

其中，F 为SMA 丝的非线性阻尼恢复力，由线性恢复力αk 和滞回恢复力(1-α)k 组成，α 为SMA 丝屈服后刚度与弹性刚度的比值，k 为SMA 丝弹性刚度，x(t)为SMA 的线性位移，z(t)为SMA 非线性滞回位移，A、β 和γ 为影响滞回环形状和大小的模型参数，n 为影响滞回曲线光滑程度的模型阶数。该模型的特点是计算简单，能够描述阻尼器在低速时的非线性性能、力-位移关系和耗能性能等。

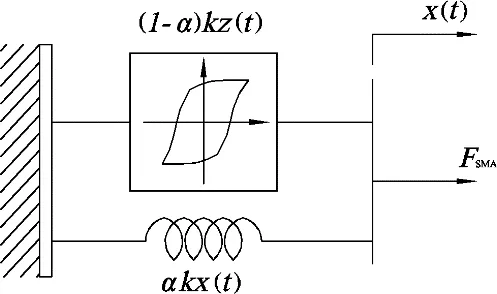
图7 Bouc-Wen 力学模型

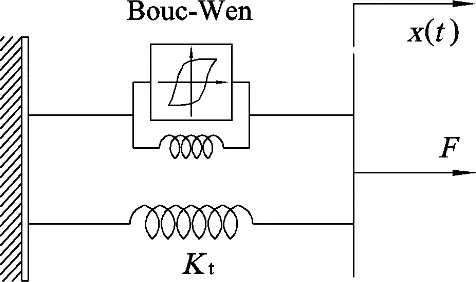
图8 一对SMA 阻尼器力学模型

所提出SMA 阻尼器的控制力除了一部分由SMA 丝组提供外，另一部由预压弹簧提供。SMA-SMPD 系统中一对SMA 阻尼器力学模型如图8 所示，控制力如式(7)所示，

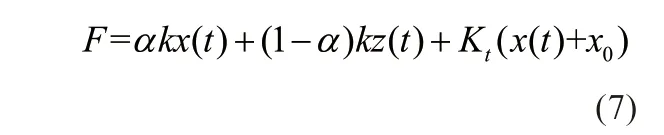
式中，各参数含义同式(4)、(5)和(6)。

4 SMA-SMPD 系统参数分析

利用Bouc-Wen 模型对SMA-SMPD系统进行参数分析，总控制力表达式中包 括A、α、β、γ、n、k、Ft和Kt等8 个参数。其中，n 为影响滞回曲线屈服点前后光滑程度的模型阶数，Wen 假设其取值为整数，越小曲线越光滑，本文中取n=1 进行分析。在Simulink 中搭建基于Bouc-Wen 模型的SMA-SMPD 系统力学模型，采用定参量分析法来分析其余参数对SMA-SMPD 系统滞回曲线特征的影响，分析一个参数变化影响时，先固定其它参数值，对该参数取不同值，再输入幅值4mm 的正弦激励，得到不同的滞回曲线，如图9-15 所示。

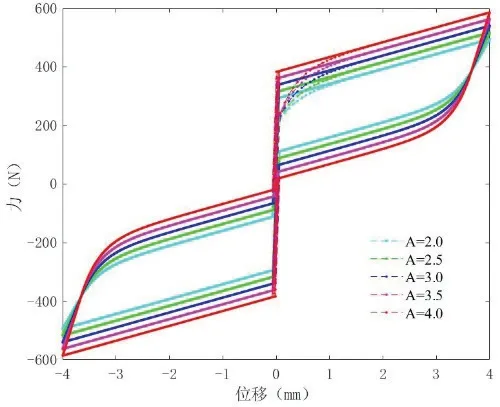
图9 参数A 对滞回曲线影响

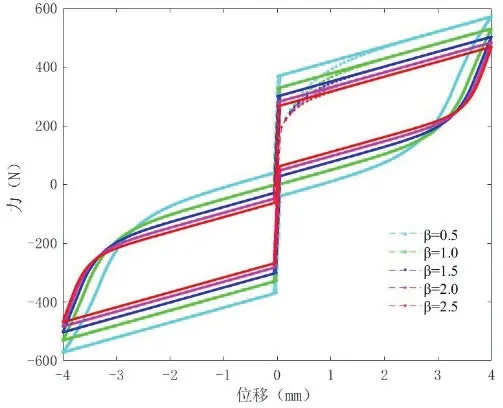
图10 参数β 对滞回曲线影响

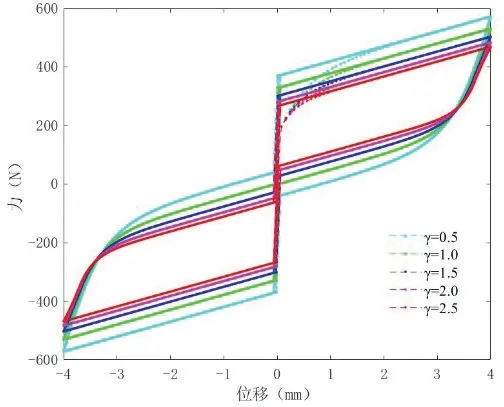
图11 参数γ 对滞回曲线影响

参数A 是与阻尼器最大输出力相关的比例系数，控制滞回曲线面积，A 越大，滞回环面积越大，耗能能力越强；参数β 和γ 是控制滞回曲线形状的参数，分别控制模型的非线性刚度和非线性阻尼，随着β 和γ 取值的增大，滞回环面积逐渐减小，耗能能力降低。

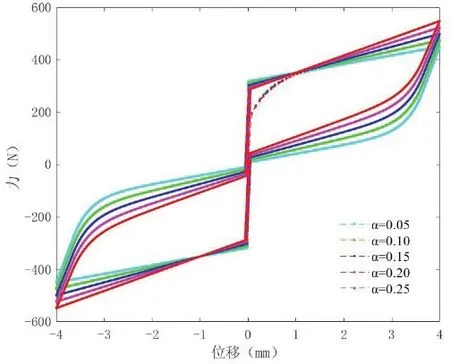
图12 参数α 影响

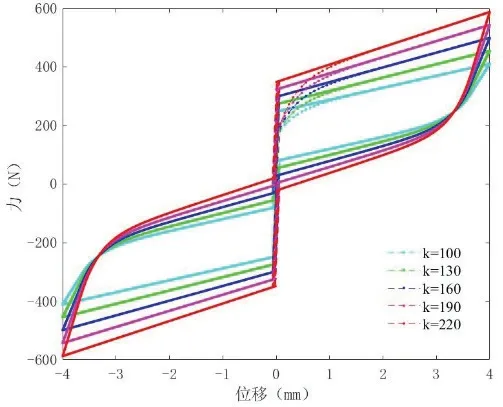
图13 参数k 影响

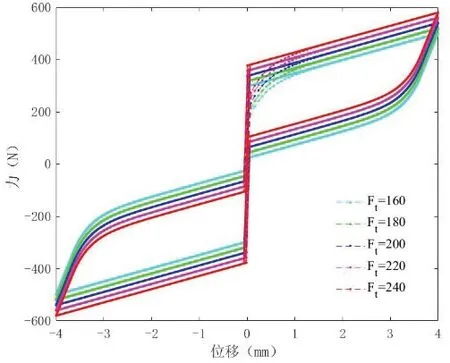
图14 参数Ft 影响

参数α 和k 的取值与SMA 有关，α是SMA 的屈服后刚度与线性刚度的比值，取值在0 和1 之间，主要影响模型的屈服后刚度，随着α 取值的增大，滞回曲线以屈服点为圆心，发生逆时针旋转，屈服后刚度增大，滞回环变的尖扁，耗能能力降低；参数k 是SMA 的线性刚度，随着取值的增大，滞回曲线以原点为中心逆时针向上倾斜，滞回环面积增大，耗能能力增强，阻尼器控制力明显增加。

图15 参数Kt 影响

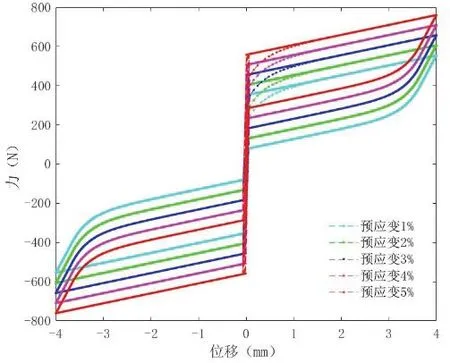
图16 预应变影响

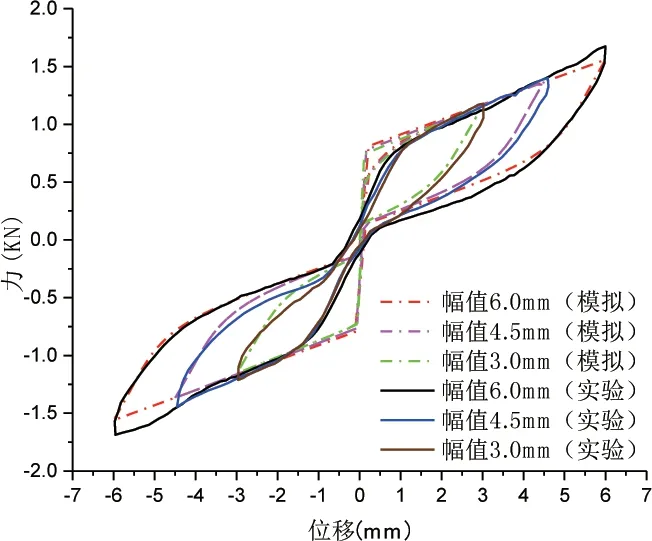
图17 优选SMA-SMPD 滞回曲线

参数Ft是弹簧预压力，主要影响SMA 阻尼器的屈服力，随着取值的增大，滞回曲线整体上移，屈服力和控制力增加，滞回环面积不变；参数Kt是弹簧刚度，随着取值的增加，阻尼器屈服后刚度增大，控制力增大；随着对SMA 预应变的增加，可以为阻尼器提供较大的恢复力，在阻尼器较小的拉伸变形下能获得较大的滞回耗能能力。

利用所提出的SMA-SMPD 系统的恢复力模型对相同条件下的试验结果进行对比，如图16 所示，两者吻合程度非常好，证明了所提出的恢复力模型的正确性和有效性。

5 结论

针对风电塔架结构的特点设计了一个智能SMA-SMPD 系统，在研究其细部构造和工作原理的基础上，利用Matlab 中的Simulink 工具箱建立了基于Bouc-Wen 模型的SMA-SMPD 系统力学模型，通过输入正弦激励进行了仿真分析，不同参数取值对SMA-SMPD 系统力学模型有一定的影响。(1) Bouc-Wen模型能够很好地描述SMA-SMPD 系统在低速时的非线性性能、力-位移关系以及良好的耗能性能；(2)预压弹簧能够对SMA-SMPD 系统提供良好的自复位功能；(3) 智能材料SMA 以其独特的超弹性、高阻尼、可恢复大变形等性能在结构振动控制领域中应用前景广阔。