西洋参分段式热风干燥动力学模型构建

吴小华，马渊博，宁旭丹，王 鹏，张振涛

西洋参分段式热风干燥动力学模型构建

吴小华1，马渊博1，宁旭丹1，王 鹏1，张振涛2

（1. 北京石油化工学院，深水油气管线关键技术与装备北京市重点实验室, 北京 102617；2. 中国科学院理化技术研究所，北京 100080）

针对直接将干燥时间带入干燥动力学模型无法准确得到分段式干燥各干燥阶段水分比的问题，提出了一种适用于分段式干燥的干燥动力学模型计算方法，可用于分析分段式干燥过程中水分比变化规律。对西洋参进行了干燥试验研究并对试验结果进行了非线性拟合，表明Modified Page模型适用于西洋参热风干燥的干燥动力学；通过对干燥条件和干燥常数的线性回归分析得到了偏回归系数，基于该偏回归系数对西洋参分段式干燥过程进行分析，得到了西洋参分段式热风干燥中各段的干燥动力学模型。利用所提出的计算方法对西洋参分段式干燥过程中水分比变化情况进行了计算，并将计算结果与西洋参分段式热风干燥试验结果进行了对比分析，发现计算结果与试验结果最大相对误差为7.44%，平均相对误差仅为1.78%。表明所提出的分段式干燥动力学模型计算方法可用于分析西洋参干燥过程中的水分比变化。

干燥；动力学；模型；分段式干燥；水分比；西洋参

0 引 言

热风干燥是应用最广泛的农产品加工方法之一[1]。常用热风干燥包括干燥条件不变的一段式干燥和干燥条件变化的分段式干燥[2]。一段式干燥是在干燥过程中干燥条件（温度、相对湿度等）始终不变的干燥方法；分段式干燥是指基于物料的干燥特性，将干燥过程分为不同的阶段，每一阶段依据工艺要求干燥条件发生相应变化的干燥方法[3]。分段式干燥过程的条件设定充分考虑了物料的干燥特性，有利于提高干燥产品品质，缩短干燥时长，降低干燥能耗[4]，是一种广泛应用于实际干燥生产的方法。

干燥动力学模型可用于分析干燥过程中物料水分变化规律[5]，阐明物料的干燥规律，为干燥工艺的制定提供依据。最常用的理论模型是基于Fick第二定律的扩散模型，该模型可用来描述降速干燥过程[6]。但扩散模型的方程形式复杂，应用不方便。研究人员在扩散模型的基础上，结合干燥动力学试验提出了多种半经验模型，主要包括Henderson and Pabis模型，Lewis模型，Page模型，以及Modified Page模型等[6-7]。这些半经验模型是理论模型的简化式，方程形式较为简单，同时可较为准确的分析干燥物料水分蒸发规律，因而得到了广泛的应用[8]。现阶段国内外众多学者已针对干燥动力学模型展开广泛研究。王凤贺等[9]研究了油茶籽热风干燥特性，比较了多种干燥模型在油茶籽干燥中的适用性，发现Lewis模型在油茶籽热风干燥中适用性最高。钱旺等[10]进行了太阳能牧草干燥动力学研究，并借助干燥动力学模型优化了太阳能牧草干燥工艺。于镇伟等[11]研究了干燥温度对有机污泥干燥速率及其他干燥特性参数的影响，并最终确定Logarithmic模型在有机污泥干燥中适用性较高。Dotto等[12]利用干燥动力学模型，研究了木瓜种子干燥过程中的传质过程，分析了不同温度和含水率对有效扩散系数的影响。Nadi等[13]研究了苹果真空干燥过程中的含水率变化规律并建立了干燥动力学模型。Amer等[14]研究了黄春菊在太阳能干燥下的水分变化规律并建立干燥动力学模型。Andrade等[15]对芒果种子干燥进行了干燥动力学模型研究，发现芒果种子活化能与木质纤维素相似。Xiao等[16]通过西洋参干燥动力学模型研究了西洋参干燥过程颜色的变化规律。Jian等[17]针对红芸豆在不同温度及相对湿度条件下干燥的水分变化规律拟合得出Modified Page模型是描述红芸豆干燥过程的最佳干燥动力学模型，并研究了新的干燥动力学模型评测方法。已有大量文章和研究都对干燥物料进行了干燥动力学模型分析并进行干燥特性研究、工艺设计和设备应用[5-19]，但对如何准确应用干燥动力学模型分析分段式干燥过程分析不够深入，难以应用干燥动力学模型分析分段式干燥过程。

针对分段式干燥无法直接将干燥时间带入干燥动力学模型求得各干燥阶段水分比的问题，本文提出了一种适用于分段式干燥的干燥动力学模型计算方法，并以西洋参为例进行分段式干燥试验，将试验结果与该方法计算结果进行对比，验证该方法准确性，以期为预测干燥过程中西洋参水分变化及设计西洋参干燥工艺提供参考。

1 分段式干燥动力学模型计算方法研究

1.1 常用干燥动力学模型

物料干燥受介质温度、相对湿度[17]等干燥条件和物料尺寸、组织结构[20]，化学成分等物料本身特性的影响，是一个复杂的传热传质过程。研究干燥物料的干燥模型对分析干燥规律，改进干燥工艺参数有重要意义。常用的干燥模型有Lewis、Page、Modified Page、Henderson and Pabis等[21]，其模型表达式如表1所示。

表1 常用干燥动力学模型

注：MR代表水分比；代表干燥时间，h；、、分别为干燥模型中干燥常数。

Note: MR stands for moisture ratio;stands for drying time, h;,andare the drying constants in the drying model.

1.2 常用参数介绍

干燥动力学模型描述物料含水率的主要参数包括水分比（MR）和干基含水率（M）。物料的水分比（MR）的计算方法如式（1）所示[22]

式中MR为水分比；M为任意时刻的干基含水率，g/g；M为干燥到平衡时的干基含水率，g/g；M为初始干基含水率，g/g。

干基含水率M的计算公式如式（2）所示

式中W为任意时刻总质量，g；为干物质质量，g。

1.3 分段式干燥动力学模型计算方法研究

干燥动力学模型方程是描述干燥时间与物料水分比之间关系的连续方程。在分析过程中，对采取的干燥物料的水分比变化规律与常用干燥模型拟合得出一种最为符合的干燥动力学模型。在干燥过程中，干燥条件（温度、相对湿度等）不同，干燥动力学模型的干燥常数也不相同。

在一段式干燥过程中，将干燥条件对应的干燥常数和干燥时间直接代入干燥动力学模型方程即可求得该干燥过程中任意时刻对应的水分比。但在分段式干燥过程中，由于各阶段干燥条件不同，干燥动力学模型中的干燥常数也不相同。将阶段交替时间分别代入先后两阶段干燥常数不同的干燥动力学模型会发现，对于同一时间，在阶段交替前后水分比不同，这与实际干燥水分比连续变化的情况不符。如图1所示，图中纵轴表示水分比，横轴表示干燥时间，曲线是分段式干燥第一阶段干燥条件下干燥动力学模型曲线，段为第一阶段实际干燥过程，用时Δt，曲线是分段式干燥第二干燥阶段干燥条件下干燥动力学模型曲线。当第一阶段干燥结束向第二阶段干燥过程转变时，处于同一时刻的点与点水分比不同，与实际干燥过程不符。

注：曲线A为分段式干燥第一阶段干燥条件下干燥动力学模型曲线；曲线B为分段式干燥第二干燥阶段干燥条件下干燥动力学模型曲线；点o为干燥过程起始点；点p为第一阶段干燥结束时的水分比状态点；点q是与p点干燥时间相同但采用第二阶段干燥条件干燥的水分状态点。

针对上述问题，提出了一种分段式干燥动力学模型计算方法，将分段式干燥过程中水分比相同的两点视为连续的两点，即将干燥条件参数代入干燥动力学模型计算时，前后两阶段交替点变为模型水分比相同的两点，而非不同干燥常数的干燥动力学模型中同一时刻的两点。基于以上理解，现认为在分段式干燥工艺中，不同阶段模型中物料同一水分对应的干燥时间不同。因此，以Page模型为例进行分段式干燥不同阶段间时间关系换算，如式（3）、（4）、（5）所示，求得同一水分比在不同干燥条件对应干燥模型中与时间的对应关系。式中下标1、2代表所处干燥阶段。其余干燥模型阶段间时间换算关系如表2所示，其中1、2代表分段式干燥中阶段交替点分别在前后两阶段的干燥动力学模型中对应的时间。干燥前一阶段干燥至1时结束，需要将1换算至2再带入下一段干燥动力学模型。

式中1，1为第一阶段干燥条件对应的干燥常数；2，2为第二阶段干燥条件对应的干燥常数；1为阶段交替点在第一阶段干燥模型中对应干燥时间，h；2为阶段交替点在第二阶段干燥模型中对应干燥时间，h。

根据上述公式原理，将分段式干燥常用干燥动力学模型时间换算如表2所示。

表2 分段式干燥常用模型时间换算关系

注：1为阶段交替点在前一阶段干燥模型中对应的干燥时间，h；2为阶段交替点在后一阶段干燥模型中对应的干燥时间，h；1、1、1分别为前一阶段干燥模型中干燥常数；2、2、2分别为后一阶段干燥模型中干燥常数。

Note:1is the drying time corresponding to the phase change point in the previous drying model, h;2is the drying time corresponding to the phase change point in the latter drying model;1,1and1are the drying constants in the previous drying stage;2,2and2are the drying constants in the latter drying stage.

分段式干燥虽然在各阶段干燥条件发生了变化，但干燥过程中水分比的变化依然是一个连续的过程，即阶段交替时前一阶段结束点与下一阶段起始点时间连续，水分比相同，因此当水分比变化图中横轴代表时间段、纵轴代表水分比时，阶段交替点两条曲线会交叉重合。如图2所示，横轴代表干燥所耗时间，纵轴代表水分比，曲线是分段式干燥第一干燥阶段干燥条件下干燥动力学模型水分比变化曲线，段为第一阶段实际干燥过程，用时Δop；曲线是分段式干燥第二干燥阶段干燥条件下干燥动力学模型水分比变化曲线，第二阶段干燥起始点为，其与点的水分比相同，第二阶段干燥过程用时Δrs。全部干燥用时为第一阶段干燥用时Δop与第二阶段干燥用时Δrs之和。

注：点r是与p点水分比相同但干燥的水分状态点；点s是以r为阶段起点进行第二阶段干燥后的干燥终点。

为应用干燥动力学模型分析分段式干燥，需要在干燥阶段交替时根据前一干燥阶段结束时的水分比换算出后一阶段在干燥动力学模行中的起始时间，各阶段的干燥时间之和即为总干燥时长。

2 西洋参干燥试验研究

西洋参是一种较为名贵的中药，目前常用热风干燥技术干燥西洋参[23]。由于西洋参干燥品质要求较高，常采用分段式干燥加工工艺[24]。为验证所提出的分段式干燥动力学模型计算方法，现以西洋参为例，需先进行多组干燥条件不同的一段式干燥试验[25]，建立干燥动力学模型；之后再进行西洋参分段式验证干燥试验，利用建立的干燥动力学模型和本文提出的分段式干燥动力学模型计算方法计算分段式干燥过程中的水分比变化。对计算结果与试验结果间进行对比分析，验证计算方法准确性。本研究的试验条件包括温度、相对湿度和西洋参直径[26-27]。

2.1 试验设备

KK/HWS-系列恒温恒湿试验箱，系统通过内部热泵蒸发器冷凝除湿，控制精度为温度±0.5 ℃、相对湿度±3%、风速2 m/s，南京贝登医疗股份有限公司；JA203H型电子天平，精度±0.001 g、XY-100MW卤素水分测定仪，精度±0.001 g，常州幸运电子设备股份有限公司。

2.2 试验材料

试验采用吉林省长白山的西洋参，于2018年9月采购，选择大小均匀、色泽一致，新鲜且无虫蛀、发霉等损坏现象的新鲜4年生西洋参，西洋参初始含水率约为68%。

2.3 西洋参干燥试验设计

为建立西洋参干燥动力学模型，验证本文提出计算方法，分别设计了8组一段式西洋参干燥试验和一组多段式验证试验。一段式试验影响因素主要包括气流温度，气流相对湿度及西洋参直径等，试验过程中风速为2 m/s，可满足验证本文所提出的分段式干燥动力学模型计算方法准确性的需求。风速作为热风干燥的重要参数之一，将作为我们进一步深入开展研究的内容。各组试验对应的干燥条件如表3所示。

表3 西洋参一段式干燥试验条件

西洋参生产中常用干燥温度范围为32～42 ℃，本试验设置温度范围为32～45 ℃，相对湿度范围为20%～40%，直径范围包括10、15、20、25 mm共4种规格，共进行了8组西洋参干燥特性试验，试验过程中每3 h记录一次物料含水率，当3 h内水分比变化值小于0.005时，认为干燥过程结束。干燥过程中各组西洋参水分比随时间变化如图3所示。

图3 西洋参干燥试验水分比变化曲线

2.4 西洋参干燥动力学模型建立

分别用Lewis、Page、Modified Page、Henderson and Pabis干燥动力学模型，对西洋参一段式试验中8组试验数据进行拟合分析，求得各干燥条件下西洋参干燥常数，并将拟合优度最高的干燥动力学模型作为西洋参干燥动力学模型。

从表4～表6中可以看出，总体上在各干燥条件下Modified Page模型决定系数2的值最高，残差平方和值更小，拟合优度最高，因此选定Modified Page模型为西洋参干燥动力学模型。

表4 温度38 ℃、相对湿度30%情况下不同直径的干燥模型对应常数项和回归系数

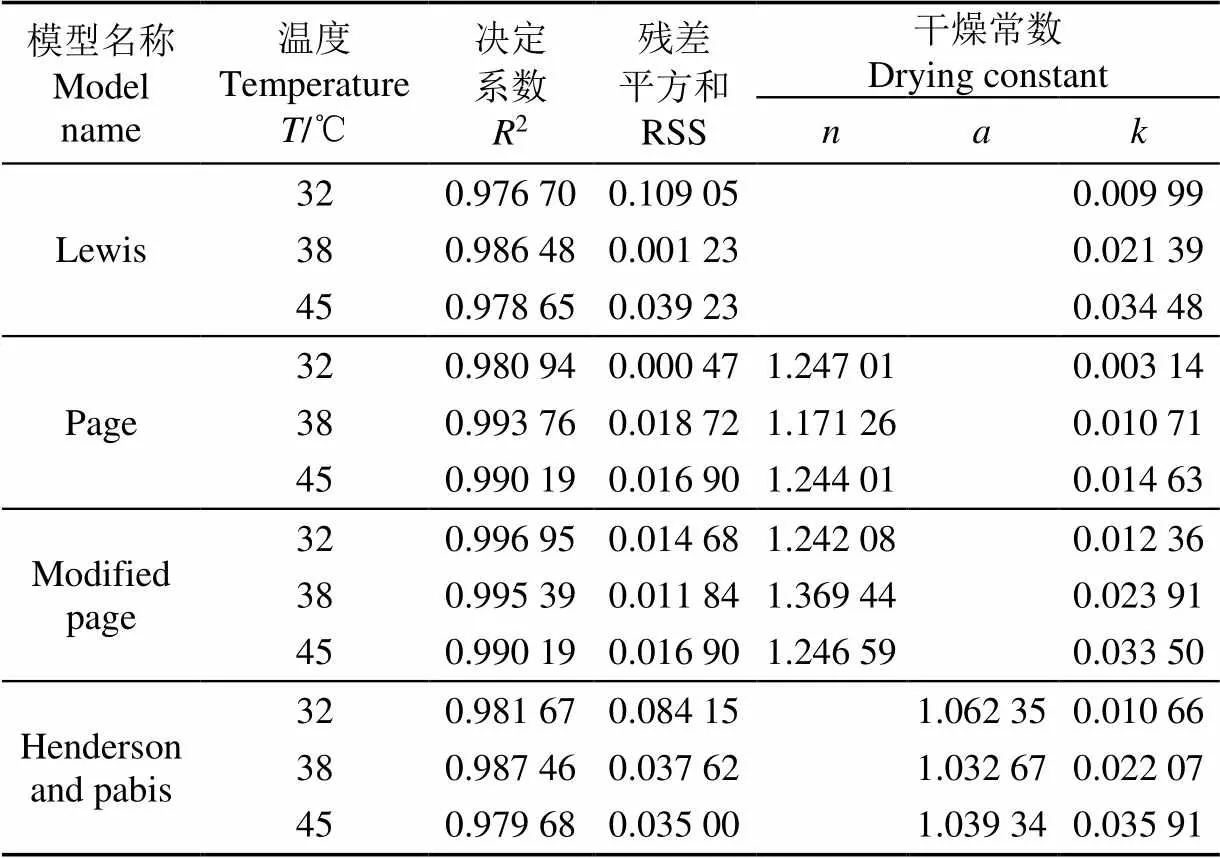
表5 直径15 mm、相对湿度30%情况下不同温度的干燥模型对应常数项和回归系数

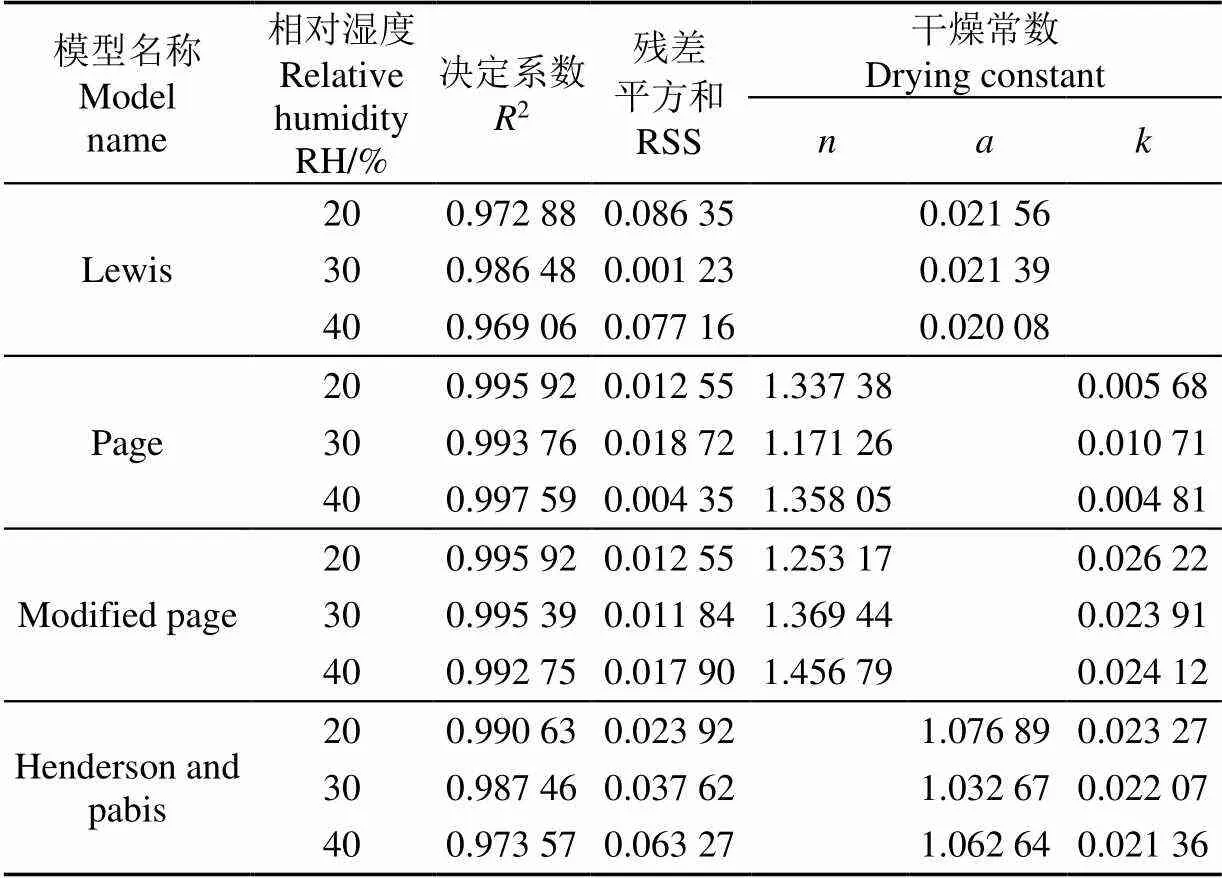
表6 直径15 mm、温度38 ℃情况下不同相对湿度的干燥模型对应常数项和回归系数

2.5 干燥条件与干燥常数关系确立

为确定干燥动力学模型中干燥常数与干燥条件之间的关系，现利用SPSS软件对干燥条件与干燥常数进行线性分析，关系可表示为

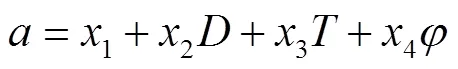
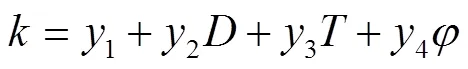
式中为温度，℃，为相对湿度，%，为西洋参直径，mm，1、2、3、4及1、2、3、4为偏回归系数。利用SPSS软件分析发现，干燥条件与干燥常数之间的显著性参数小于0.05，两者之间线性关系显著。

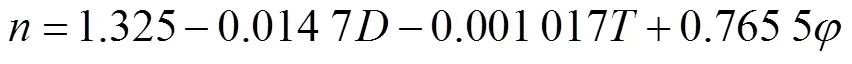
根据式（8）、（9）分析结果，即可得到在温度32～45 ℃、相对湿度20%～40%、直径10～25 mm时，西洋参热风干燥动力学模型干燥常数。当干燥条件超出这一范围时，式（8）和式（9）将不再适用。上述范围是经充分调研吉林省抚松地区西洋参加工企业工程技术人员后确定的，已尽可能包含道地高品质西洋参干燥加工适用的温湿度范围。

3 分段式干燥动力学模型计算方法验证

3.1 西洋参分段式干燥验证试验

在广泛调研抚松地区高品质西洋参加工工艺后发现，在西洋参实际干燥加工工程中，为保证加工后西洋参的切片品质，一般采用从低温向高温逐步升温的分段式干燥工艺。本文试验设计参照了这一加工过程。

分段式试验中干燥条件随时间变化，试验条件如表7所示。试验过程中记录西洋参的初始质量，并每隔3 h测量西洋参实时质量，将测量结果按式（1）和式（2）进行干基含水率及水分比的换算，得出水分比变化规律，如图4所示。

表7 分段式西洋参干燥试验条件

图4 西洋参分段式干燥试验水分比变化曲线

3.2 分段式干燥动力学模型计算方法验证

本文研究重点是提出了一种适用于分段式干燥的干燥动力学模型构建和计算方法研究，并对该方法进行验证。最佳干燥工艺不是本文研究的重点，但本文提出的适用于分段式干燥的干燥动力学模型构建和计算方法研究可为最佳工艺设计过程中的水分比预测提供借鉴。

为验证所提出的分段式干燥动力学模型计算方法的准确性，依据表7所列试验条件，用所提出的分段式干燥动力学模型对西洋参水分比进行计算，并将分段式干燥水分比变化情况计算结果与试验结果进行了对比研究，如表8所示。

实际干燥时间指在干燥过程中的实际用时；模型换算时间是指根据该点水分比换算出的对应阶段的恒定条件干燥模型中的时间，供分段式干燥模型计算使用。

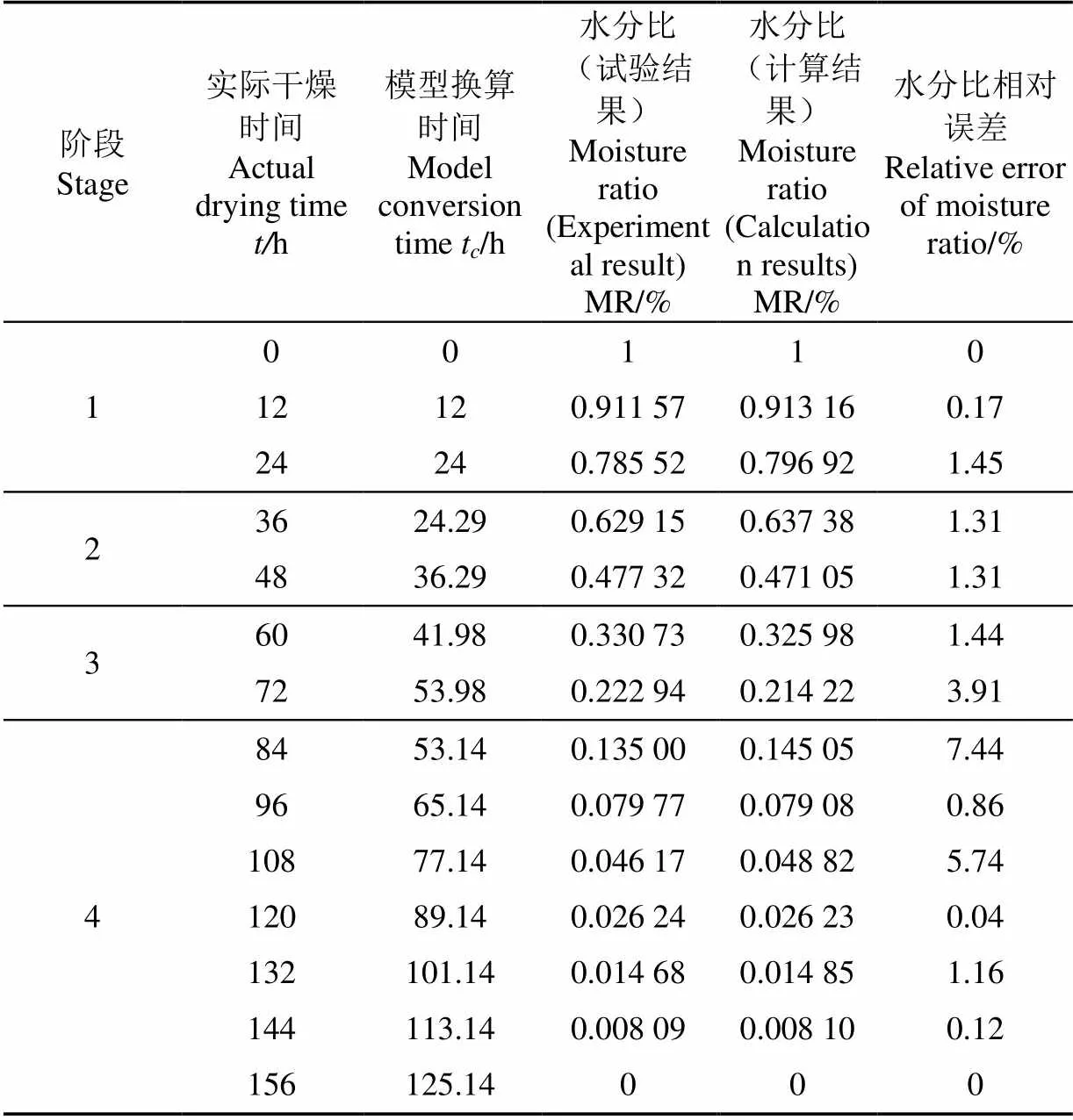
表8 计算结果与试验结果对比

由表8可以看出，计算结果与试验结果最大相对误差为7.44%，平均相对误差仅为1.78%，其平均相对误差较小且仅出现一次较大相对误差。分析结果表明本文所提出的分段式干燥动力学模型计算方法可用于预测分段式干燥物料水分比变化，且由于西洋参分段式干燥验证试验结果与所提出的分段式干燥动力学模型计算方法计算所得的结果吻合较好，未进行重复性试验。

4 结 论

1）为解决将干燥时间直接代入分段式干燥各段干燥动力学模型时会出现的同一时刻计算得到的水分比不同问题，提出了一种分段式干燥动力学模型计算方法，适用于分段式干燥过程中水分比变化规律分析。

2）以西洋参为例，开展了西洋参干燥特性试验，建立了西洋参干燥动力学模型。以干燥温度、相对湿度和西洋参直径为变量，进行了多组一段式西洋参干燥试验研究，对试验数据的拟合发现Modified Page模型是最适用于西洋参热风干燥的干燥动力学模型；通过对干燥条件和干燥常数进行线性回归分析，得到了偏回归系数；基于该偏回归系数对西洋参分段式干燥过程进行分析，得到了西洋参分段式热风干燥中各段的干燥动力学模型，并结合本文提出的计算方法进行了分段式干燥过程中水分比计算。

3）开展了西洋参分段式热风干燥验证试验，试验结果与采用本文所提出的计算方法得到的计算结果对比发现，平均相对误差仅为1.78%，表明所提出的分段式干燥动力学模型计算方法可用于分析西洋参干燥过程中的水分比变化，对分析分段式干燥过程水分变化，优化西洋参干燥工艺具有指导意义。

由于干燥能耗与品质指标不是本文研究关注的重点，没有专门针对干燥能耗与品质指标开展研究。

[1] 朱文学. 食品干燥原理与技术[M]. 北京：科学出版社，2009.

[2] 吴中华，李文丽，赵丽娟，等. 枸杞分段式变温热风干燥特性及干燥品质[J]. 农业工程学报，2015，31(11)：287－293.

Wu Zhonghua, Li Wenli, Zhao Lijuan, et al. Drying characteristics and product quality of Lycium barbarum under stages-varying temperatures drying process[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(11): 287－293. (in Chinese with English abstract)

[3] 王庆惠，李忠新，杨劲松，等. 圣女果分段式变温变湿热风干燥特性[J]. 农业工程学报，2014，30(3)：271－276.

Wang Qinghui, Li Zhongxin, Yang Jinsong, et al. Dried characteristics of cherry tomatoes using temperature and humidity by stages changed hot-air drying method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(3): 271－276. (in Chinese with English abstract)

[4] 朱德泉，马锦，蒋锐，等. 山核桃坚果分段变功率微波干燥工艺参数优化[J]. 农业工程学报，2016，32(15)：268－274.

Zhu Dequan, Ma Jin, Jiang Rui, et al. Parameter optimization of hickory nut drying by phased varying power microwave[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(15): 268－274. (in Chinese with English abstract)

[5] 唐小闲. 马蹄淀粉微波间歇干燥特性及工艺优化研究[D].大连：大连工业大学，2017.

Tang Xiaoxian. Research on Intermittent Microwave Drying Properties and the Process Optimization of Water Chestnut Starch[D]. Dalian: Dalian Polytechnic University, 2017. (in Chinese with English abstract)

[6] Giraudo A, Valentini N, Venturello A, et al. Kinetic modeling of hazelnut drying: Effects of different cultivars and drying parameters[J]. Journal of Food Process Engineering, 2018, 41(1): 1－9.

[7] 王汉羊，刘丹，于海明. 山药微波热风耦合干燥特性及动力学模型[J]. 食品科学，2018，39(15)：115－121.

Wang Hanyang, Liu Dan, Yu Haiming. Drying characteristics and kinetic model of chinese yam using microwave coupled with hot air[J]. Journal of Food Science, 2018, 39(15): 115－121. (in Chinese with English abstract)

[8] 杨潇潇，丛堃林，张衍国，等. 木薯高/低温二段式干燥工艺参数优化试验[J]. 农业工程学报，2018，34(2)：272－277.

Yang Xiaoxiao, Cong Kunlin, Zhang Yanguo, et al. Optimization experiment on two-stage drying process of high and low temperatures for cassavas[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 272－277. (in Chinese with English abstract)

[9] 王凤贺，丁冶春，陈鹏枭，等. 油茶籽热风干燥动力学研究[J]. 农业机械学报，2018，49(S1)：433－439.

Wang Fenghe, Ding Yechun, Chen Pengxiao, et al. Investigation on hot-air drying of camellia oleifera seeds[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(S1): 433－439. (in Chinese with English abstract)

[10] 钱旺，杨世昆，刘贵林，等. 太阳能牧草干燥成套设备干燥工艺参数优化[J]. 农业机械学报，2018，49(8)：110－118.

Qian Wang, Yang Shikun, Liu Guilin, et al. Optimization of drying process parameters of solar herbage dry equipment [J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(8): 110－118. (in Chinese with English abstract)

[11] 于镇伟，陈坤杰，高崎，等. 有机污泥干燥特性与干燥模型研究[J]. 农业机械学报，2017, 48(10)：291－296.

Yu Zhenwei, Chen Kunjie, Gao Qi, et al. Drying characteristics and mathematical modeling of organic sludge[J]. Transactions of the Chinese society for Agricultural Machinery, 2017, 48(10): 291－296. (in Chinese with English abstract)

[12] Dotto G L, Meili L, Tanabe E H, et al. Evaluation of the mass transfer process on thin layer drying of papaya seeds from the perspective of diffusive models[J]. Heat and Mass Transfer, 2018, 54(2): 463－471.

[13] Nadi F, Tzempelikos D. Vacuum drying of apples (cv. Golden Delicious): Drying characteristics, thermodynamic properties, and mass transfer parameters[J]. Heat & Mass Transfer, 2018(4): 1－14.

[14] Amer B M A, Gottschalk K , Hossain M A . Integrated hybrid solar drying system and its drying kinetics of chamomile[J]. Renewable Energy, 2018, 121: 539－547.

[15] Andrade L A , Barrozo M A S , Vieira L G M . Pyrolysis of mango residues: a statistic analysis on nonlinear models used to describe the drying stage[J]. Waste & Biomass Valorization, 2018(7): 1－8.

[16] Xiao H W, Law C L, Sun D W, et al. Color change kinetics of American ginseng () slices during air impingement drying[J]. Drying Technology, 2014, 32(4): 418－427.

[17] Jian F, Jayas D S. Characterization of isotherms and thin-layer drying of red kidney beans, Part I: Choosing appropriate empirical and semitheoretical models[J]. Drying Technology, 2018, 36(14): 1－11.

[18] Lakshmi D V N , Muthukumar P, Layek A, et al. Drying kinetics and quality analysis of black turmeric () drying in a mixed mode forced convection solar dryer integrated with thermal energy storage[J]. Renewable Energy, 2018, 120: 23－34.

[19] Behera G, Sutar P P. A comprehensive review of mathematical modeling of paddy parboiling and drying: Effects of modern techniques on process kinetics and rice quality[J]. Trends in Food Science & Technology, 2018, 75: 206－230.

[20] 孙传祝，石东岳，王相友，等. 单片物料厚度对胡萝卜红外薄层干燥水分迁移的影响[J]. 食品科学，2017, 38(13)：53－59.

Sun Chuanzhu, Shi Dongyue, Wang Xiangyou, et al. Effect of single material thickness on moisture transfer during infrared thin-layer drying of carrot[J]. Journal of Food Science, 2017, 38(13): 53－59. (in Chinese with English abstract)

[21] 张绪坤，刘胜平，吴青荣，等. 污泥低温干燥动力学特性及干燥参数优化[J]. 农业工程学报，2017，33(17)：216－223.

Zhang Xukun, Liu Shengping, Wu Qingrong, et al. Drying kinetics and parameters optimization of sludge drying at lowtemperature[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(17): 216－223. (in Chinese with English abstract)

[22] 马怡童，朱文学，白喜婷，等. 超声强化真空干燥全蛋液的干燥特性与动力学模型[J]. 食品科学，2018，39(3)：142－149.

Ma Yitong, Zhu Wenxue, Bai Xiting, et al. Drying characteristics and kinetic model of liquid whole egg during ultrasound-reinforced vacuum drying[J]. Journal of Food Science, 2018, 39(3): 142－149. (in Chinese with English abstract)

[23] Wilhelm L R. Ginseng drying-the effect of drying air temperature and humidity upon quality[J]. Applied Engineering in Agriculture, 1990, 6(5): 635－639.

[24] Xiong Hui, Zhang Aihua, Zhao Qiqi, et al. Discovery of quality-marker ingredients of Panax quinquefolius driven by high-throughput chinmedomics approach[JOL]. Phytomedicine, [2019-10-18]. http://doi.org/10.1016/j.phymed.2019.152928.

[25] 李绚阳，李保明，郑炜超，等. 鸡粪中低温干燥动力学特性与参数优化[J]. 农业工程学报，2018，34(10)：194－199.

Li Xuanyang, Li Baoming, Zheng Weichao, et al. Middle-low temperature drying dynamic characteristics for poultry manure and its parameter optimization[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(10): 194－199. (in Chinese with English abstract)

[26] Xiao Hongwei, Bai Junwen, Xie Long et al. Thin-layer air impingement drying enhances drying rate of American ginseng () slices with quality attributes considered[J]. Food and Bioproducts Processing, 2015, 94: 581－591.

[27] 楚文靖，盛丹梅，张楠，等. 红心火龙果热风干燥动力学模型及品质变化[J]. 食品科学，2019，40(17)：150－155.

Chu Wenjing, Sheng Danmei, Zhang Nan, et al. Hot-air drying of red-fleshed pitaya: kinetic modelling and quality changes[J]. Journal of Food Science, 2019, 40(17): 150－155. (in Chinese with English abstract)

Construction of staged hot-air drying dynamic model for American ginseng

Wu Xiaohua1, Ma Yuanbo1, Ning Xudan1, Wang Peng1, Zhang Zhentao2

(1.&,,102617,; 2.,,100080,)

American ginseng is a perennial herb of the genus ginseng. Its rhizome can be used as medicine, and it is a traditional and precious Chinese medicinal material. In addition, it has also been favored as a health product. Research indicates that the rhizomes, leaves, flowers and fruits of American ginseng are rich in biologically active constituents, including ginsenoside, polysaccharide, various amino acids, vitamins, volatile oil, minerals and other chemical components, which are conducive to anti-aging and enhance human immunity. Hot air drying is a key step for the processing of American ginseng, which is divided into two categories: constant condition drying and stages-varied drying. Among the two methods, the stages-varied drying process is widely used in drying production, which contains multiple drying stages and different drying conditions at each stage. The drying characteristics of the materials are fully considered in the condition setting of stages-varied drying, which is conducive to improve the drying quality and save energy in the drying process. The drying kinetic model can reveal the change rule of moisture ratio of materials and provide scientific basis for the development of drying processes. Under the condition of constant temperature drying, the accurate moisture content of materials can be obtained by directly considering the drying parameters in the existing dynamic model of hot air drying. However, since the drying conditions are different at each stage of stages-varied drying, the drying constants are different at each stage in the drying model. In traditional studies, the moisture ratio at each drying stage cannot be accurately obtained if the drying timeof stages-varied drying is directly taken into account in the drying kinetics model. To solve this problem, a calculation method of drying kinetics model for the stage-varied drying was proposed, which can accurately analyze the variation of moisture ratio during the stages-varied drying process. In order to establish the method, the drying experiment of American ginseng was carried out and the experimental results were fitted. The results showed that the Modified Page model was the best drying kinetic model for the hot-air drying of American ginseng. The partial regression coefficient was obtained by linear regression analysis of drying conditions and drying constants. Based on the partial regression results, the stage-varied drying process of American ginseng was analyzed and the drying kinetics model for each stage of American ginseng stages-varied drying was obtained. By using the proposed calculation method, the change of moisture ratio in the stages-varied drying process of American ginseng was calculated and compared with the results of the American ginseng stages-varied hot-air drying experiment. It was found that the maximum relative error between the calculation results and the experimental results was 7.44%, the average relative error was only 1.78%. The results indicate that the proposed stages-varied drying kinetic model calculation method can be used to analyze the change of the moisture ratio in the drying process of agricultural products.

drying; kinetic; models; stages-varied drying; moisture ratio; American ginseng

2019-11-01

2020-02-20

国家重点研发计划资助项目（2018YFD0700200）；北京市高水平创新团队建设计划项目（IDHT20170507）；长城学者培养计划（CIT&TCD20180313）

吴小华，副教授，博士，主要从事能源高效利用及热泵技术开发研究。Email：wuxiaohua@bipt.edu.cn

10.11975/j.issn.1002-6819.2020.05.037

S37

A

1002-6819(2020)-05-0318-07

吴小华，马渊博，宁旭丹，王 鹏，张振涛. 西洋参分段式热风干燥动力学模型构建[J]. 农业工程学报，2020，36(5)：318－324. doi：10.11975/j.issn.1002-6819.2020.05.037 http://www.tcsae.org

Wu Xiaohua, Ma Yuanbo, Ning Xudan, Wang Peng, Zhang Zhentao. Construction of staged hot-air drying dynamic model for American ginseng[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(5): 318－324. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.05.037 http://www.tcsae.org