区域尺度农业管理分区的无监督特征选择与破碎度优化算法

黄 芬，朱金诚，张小虎，刘通宇，朱 艳

区域尺度农业管理分区的无监督特征选择与破碎度优化算法

黄 芬1,2，朱金诚1，张小虎2，刘通宇1，朱 艳2

（1. 南京农业大学信息科学与技术学院，南京 210095； 2. 南京农业大学国家信息农业工程技术中心，南京 210095）

针对区域尺度管理分区指标筛选与分区破碎问题，提出基于指标相关性聚类的无监督过滤式指标选择方法FSCC（feature selection based on correlation clustering algorithm，FSCC）与基于一致性和完整性的指标优化方法（consistency and integrity optimization，CIO）。以中国主要冬小麦种植区为研究区域，气象、土壤、地形等小麦生长相关指标为数据源，研究区域从大到小划分为4个尺度，首先选用最大方差、拉普拉斯得分2种传统过滤式特征选择方法与FSCC分别进行4个尺度的管理分区指标筛选，对比基于3种方法筛选指标集构建的管理分区划分结果，评价FSCC分区指标选择方法；其次，设计指标优化算法，对4个尺度筛选的指标集分别进行一致性与完整性分析与优化。结果表明：相较最大方差法和拉普拉斯得分法，FSCC筛选指标的分区效果具有较好表现，如皋2.5km处，其评价指标模糊性能指数（FPI）、归一化分类熵（NCE）和修正分离熵（MPE）均低于另外2种方法52.44%、49.45%和49.52%；CIO在如皋、南通尺度下有效剔除分区破碎指标，分区完整性明显，除南通10 km外，CIO比FSCC的指标集，FPI、NCE、MPE分别平均低0.078、0.061、0.082，相对提升了FSCC的分区效果。

农业；管理分区；算法；特征选择；过滤式；一致完整性优化；区域尺度

0 引 言

管理分区是对具有相似地形、土壤和作物特征的区域定义与划分[1]。农作管理分区按照区划尺度可分为田块尺度和区域尺度，目前，田块尺度的管理分区研究多针对田块内部土壤（肥力、墒情）及作物长势（苗情、虫情、病情等）的差异制定田块内部基本的管理单元，通过结合变量作业可推进肥水、农药的精确投放[2-3]；区域尺度的农作管理分区是根据农作投入、实施、产出等要素的空间差异研究制定合适的基本农作管理单元划分，美国制定的农作管理分区USGS-NRCS Crop management zones[4]，其区域尺度有效突破了行政区划，达到国家尺度的区域范围，可见，农作管理分区的研究已从田块尺度贯穿到“园区—区域”的全尺度范围。进行区域尺度的管理分区研究，是突破田块尺度的有益尝试，进一步的分区管理方案制定，可帮助农技人员提供大尺度的区域农事操作指导，更好的优化其服务的形式，也是目前中国农技推广改革面临的一大重要问题。黄宝荣等[5]指出管理分区遵循主导因素原则，即选取能反映区域相关特征及其影响因素分异的主导因素为确定分区边界的主要根据，因此精确、合理的分区指标选择对管理分区结果有重要影响[6]。随时间更新及研究区域尺度变化，为降低指标数据采集难度及后续分区研究的复杂度，在保留分区主导指标、保证管理分区效果的同时，应尽量缩减分区指标集。

管理分区指标的确定常采用专家主观评判法与多元统计等方法。前者依靠相关领域专家意见筛选指标，存在一定主观偏差。多元统计法的应用中[1]，Bazzi等[7-8]使用空间相关分析法进行了特定研究区域的管理分区变量选择研究；Fraisse等[9-12]引入了主成分分析方法；Córdoba等[13-14]基于莫兰指数提出了多源空间主成分分析法； Gavioli等[1]探索了管理分区的指标组合构建方法，借助产量指标对PCA、MULTISPATI-PCA等组合指标进行有监督分析，并提出新的MPCA-SC指标。上述方法基于原始指标集进行的有监督线性变换组合的新指标变量，无法有效缩减分区研究中的原始指标个数，属于机器学习研究领域的特征提取方法[15]，机器学习领域的另一降维方法——特征选择方法，通过选取原指标集的子集达到保留重要特征及降维目的。

常见特征选择有过滤式、包裹式与嵌入式3类[15]。其中，过滤式根据数据的结构特点来选择特征指标[16]，具有选择快与无需监督信息等优势，且其选择过程与后续学习器无关[15]，应用于管理分区研究，体现为分区指标选择与后续分区方法无关，可一定程度降低分区算法的复杂度。最大方差法与拉普拉斯得分法是两种传统的过滤式特征选择方法[16]。

当前管理分区研究中，分区破碎问题导致分区中孤立单元或碎片较多，不便于农机设备的田间变量管理作业[17]和区域管理方案的分配。李翔等[17]提出的分区算法SKCM，在分区阶段可有效去除大量孤立单元与碎片，但尚未涉及分区指标对分区结果破碎性影响的研究。

目前，田块尺度的管理分区多采用有监督特征提取进行指标筛选，难以有效减少原始分区指标数量，且需采集相应监督信息，同时，分区完整性的提升与处理研究中未兼容考虑指标导致的破碎性问题。本文基于相关性与AP聚类[18]提出一种新的无监督过滤式管理分区指标筛选方法FSCC；同时，提出新的分区破碎度评价指标FMZ（fragmentation of management zones，FMZ），协同Kappa系数从分区一致性与完整性角度研究提出指标集的优化方法CIO，优化FSCC指标筛选结果。

1 数据和方法

1.1 数据

1.1.1 数据来源

研究区域为中国冬小麦主要种植区，按尺度选择冬小麦主产区、江苏省、南通市、如皋市4个试验区域。下文将冬小麦主产区简称为冬麦区。

研究指标集选择气象、土壤、地形三大类。气象指标[19]包括累积有效日照时长(SSDsum)、累积有效积温[20]（GDDsum）、累积降水量（PREsum）、平均降水量（PREavg）、平均气温日较差（TDRavg）；土壤指标[21-22]包括有效磷（AP）、速效钾（AK）、全氮（TN）、有机质（OM）、酸碱度（pH值）；地形指标[23]包括高程（DEM）、坡度（SLO）、坡向（ASP）。

气象指标计算基于2000年1月－2014年7月的日最高气温、日最低气温、20-20时累积降水量和日照时数，其中，2000年1月－2010年12月采集自国家气象局“1951－2010年中国2474个国家级地面站数据更正后的月报数据文件（A0/A1/A）基础资料集”，2011年1月至2014年5月采集自各省上报至国家气象信息中心的地面月报数据文件，2014年6－7月采集自国家气象信息中心实时数据库。

土壤数据集取自中国科学院南京土壤研究所构建的中国土种数据库，来源于1978－1984年全国第二次土壤普查汇总成果，是目前时间节点和采样节点分布均为最新的全国土壤普查数据[24-25]。

地形指标计算基于数字高程模型（DEM），DEM取自地理空间数据云网站的SRTM DEM数据产品，测图任务时间为2000年2月11日－2月22日，选用中国范围90 m分辨率栅格源数据。

1.1.2 试验区域尺度划分

一定采样尺度只能揭示特征指标的某一空间结构特征[26]，尺度常通过空间范围所决定的幅度及最小可辨识单元的粒度（如采样网格大小、像元、分辨率）表现[27]。

为有效提取管理分区指标的空间尺度特征，首先对研究区域的空间幅度从小到大划分为四级：县级、市级、省级、冬麦区级，其中，县级为如皋市；市级为南通市；省级为江苏省全省；冬麦区级覆盖天津、山东全省以及北京、河北、山西、甘肃、陕西、河南、江苏、安徽省部分地区。

在空间粒度上，根据研究区域各级幅度的范围大小，从高到低确定数个空间分辨率。试验中，如皋市的粒度（分辨率）为1、2.5 km；南通市为5、10 km；江苏省为10、25 km；冬麦区级为50、100 km。下文将区域幅度统称为尺度，粒度统称为分辨率。

1.1.3 数据预处理

按照1.1.2节的尺度与分辨率设计，对气象、土壤及地形源数据分别进行4个尺度下各分辨率的栅格预处理，并通过栅格计算求取1.1.1节所需指标。对90m分辨率的地形栅格源数据，首先通过ArcGIS软件提取ASP与SLO，其次进行重采样[28]获取所需分辨率的栅格指标；气象和土壤源数据为带有空间定位信息的离散采样数据，土壤数据采用ArcGIS软件进行克里金插值[29-31]获得所需各分辨率栅格指标；气象栅格指标的计算：首先采用AUNSPLIN对2000年1月－2014年7月的原始气象数据进行空间插值[32-33]获得各年的日有效日照时长（SSD）、日有效积温（GDD）、日降水量（PRE）和气温日较差（TDR）的各分辨率栅格数据；其次，选用当年冬小麦拔节期、开花期和成熟期这3个关键生育期的日值，对SSD、GDD和PRE累计求和得到每年SSDsum、GDDsum和PREsum，对PRE和TDR累计求和并计算均值得到每年PREavg和TDRavg。其中GDD及TDR计算公式如下：

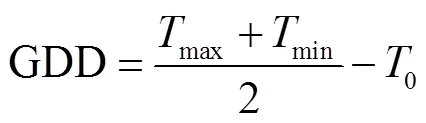
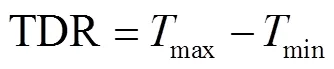
式中GDD为日有效积温，TDR为气温日较差，max为日最高气温，min为日最低气温，0为基点温度，0此处设0 ℃。

最后按各尺度各分辨率所覆盖地理范围，分别掩膜提取各气象、土壤及地形指标数据，构建原始管理分区指标集。

1.2 评价指标

1.2.1 筛选结果评价指标

模糊C均值算法FCM大量用于土壤、地形地貌和遥感数据等相关聚类中[34]，本研究选用FCM对3种筛选方法提取指标集构建管理分区，并选取3种模糊聚类效果评价指标模糊性能指数[35]（FPI），归一化分类熵[36]（NCE）和修正分离熵[37]（MPE）评价筛选分区指标的分区效果。

设为聚类簇数，FCM应用于管理分区，则对应为分区类别数，为样本数目，μ为第个样本归属于第个簇的隶属度。FPI是衡量样本在个簇间分离程度的指标，其变化范围为0到1之间，其值越小则样本在簇间的分离程度越小，分类效果越明显。

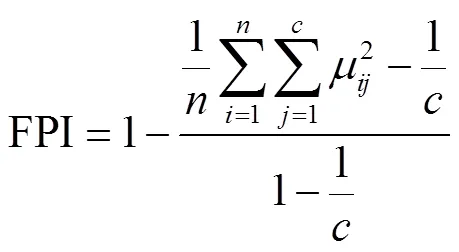
NCE是衡量样本集被划分为不同簇而造成的数据组织的破坏程度的指标，其变化范围为0到1之间。NCE的值越小，则聚类所得各管理分区内像元属性之间的相似程度越高，聚类效果越明显。

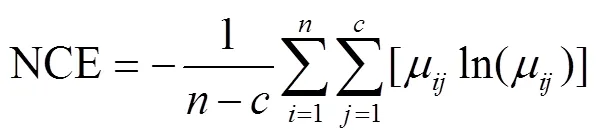
MPE是衡量各簇间模糊程度的指标。MPE值越接近0，则构造簇间模糊程度越小，聚类效果越明显。

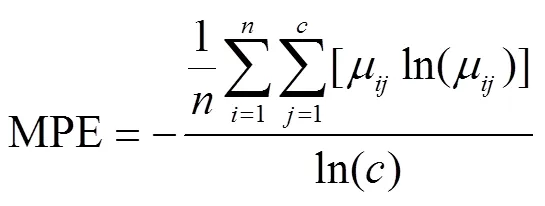
1.2.2 一致完整性优化评价指标

对FSCC筛选指标的进一步优化以保持缩减指标集前后分区的一致与完整为目的，因此引入一致性评价指标Kappa系数，提出完整性评价指标破碎度FMZ。

Kappa系数[38]用于一致性检验，其计算基于混淆矩阵，可用来比较图件[39]。Kappa系数的计算结果为-1~1。两张分区图完全一样时=1；通常≥0.75时，2图件的一致性较高，变化小；0.4≤≤0.75时一致性一般，变化明显；≤0.4时，一致性较差，变化较大[40]。

景观生态格局分析中常用聚集度和破碎度定量评价景观生态中斑块的聚集程度[17]，其算法适用于不同景观要素在同一分类图中的比较，生境破碎化指数用于描述景观中某生境类型在给定时间和给定性质上的破碎化程度[41]，但其并不适用于同一管理分区在不同分类图中的分析与评价。李翔等[17]从管理分区像元间的空间相邻性出发，选择相邻像元边个数为破碎指标，将像元边长单位化，求各斑块的周长平均值。该方法适用于同一管理分区在同一幅度、同一分辨率下分类图的分析评价，不适用于多尺度分类图评价。分区同一边长在不同分辨率下对应不同单位长度，导致破碎度随分辨率提高而增大，且该指数仅与像元边长单位化的斑块周长相关，受斑块形状影响较大。

景观斑块密度[42]可反映景观破碎化程度，其采用密度的方式可以减少尺度对破碎度衡量的影响。

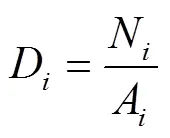
针对多尺度管理分区破碎度问题，以景观斑块密度为基础提出新的完整性评价指标破碎度FMZ。

管理分区中一个分类图被分为类分区，研究需要评价类分区在分类图中的综合破碎程度。当一类分区为一个完整斑块时，将该分区的破碎度值设为0。设第类分区的破碎度为F，斑块数为P，分区总面积为S，可得：

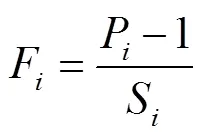
加权各分区破碎度求和，可得管理分区综合破碎度指标：

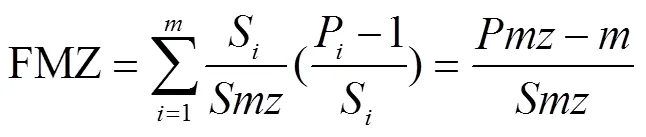
式中FMZ为管理分区综合破碎度，为分区类别数；为管理分区总面积，km2；为管理分区的总斑块数。

1.3 基于指标相关性聚类的过滤式指标选择

1.3.1 最大方差法

最大方差法（Variance）通过计算各指标方差来评价该指标所具有数据信息量的表现[16]，进行方差排序可达到无监督特征重要性评价与指标选择的目的。第个指标f的方差V越大，则该指标的值在该维度越分散，更能反映信息总体分布，f越重要；V越小，则f的值变化越小，只反映局部信息，f越不重要。

1.3.2 拉普拉斯得分法

拉普拉斯得分法（Laplacian Score）也是一种过滤式无监督特征选择算法，由He等[43]基于拉普拉斯特征映射和局部保留投影方法提出[16]。其依据各指标的分布、范围和与其邻近点的权重计算对应的拉普拉斯得分。该得分反映数据局部保存能力与局部分布情况，得分越小则特征越好[16]。在管理分区指标筛选中，指标得分越小，对应指标更重要。

1.3.3 基于相关性聚类的指标筛选FSCC

与作物生长密切相关的环境指标携带研究管理分区的有效信息，且这些环境要素间存在一定程度的相关关系[44]，其中呈强相关的指标必定表现为携带有效分区信息的重叠性[45]。

皮尔森相关系数[46]常用于度量2个变量间线性关系的强弱，其计算方法如下：

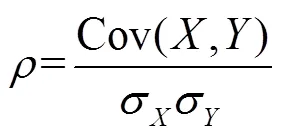
式中为皮尔森相关系数，Cov(,)为变量与变量的协方差，σ与σ为变量与变量的标准差。

FSCC首先对1.1.3节的原始管理分区指标集计算皮尔森相关系数，据此构建相关矩阵；其次，将相关矩阵行向量作为对应指标变量进行AP聚类。获取的聚类结果中，认为高度相关且整体数据关系结构高度相似的同簇指标，携带了重叠的分区有效信息，且簇中心指标可反应同簇指标的分区特征，故FSCC选取各簇中心指标构成筛选后的初始分区指标集，在去除同簇冗余指标的同时保留原有数据的整体特征。

AP聚类是一种基于近邻信息传递的聚类算法，相较于传统聚类算法具有无需给定聚类类别数的优势，避免了聚类结果受限于初始类代表点的选择，同时能很好解决非欧空间问题[47]。

1.4 基于一致性和完整性的指标优化CIO

FSCC保留了原指标集的整体特征，而导致分区破碎的指标亦可能保留。为进一步约减指标集和过滤破碎指标，从一致性与完整性角度在FSCC基础上进行优化方法的研究。CIO设计采用“后向”搜索策略，每次尝试去掉一个无关特征来逐渐缩减指标集[15]。设每轮待筛选集为父层，去掉其任意一个元素的指标集为其子层。CIO依据子层与父层对应分区图间的Kappa系数及各子层集合对应分区图破碎度FMZ，对指标集进行逐层筛选和分支选择，最终确定优化的指标集。

记FSCC筛选的初始指标集为M，kappa(,)为指标集与对应管理分区图间的Kappa系数，Tkappa为Kappa系数阈值，fra(,)为指标集与对应管理分区图破碎度FMZ的差，Tfra为破碎度差的阈值。CIO算法如下：

1）输入指标集M和，设=，M=M。为M包含的指标数。

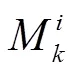
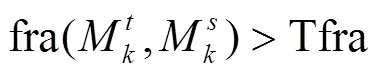
4）所有分支筛选终止时，在备选指标集中选择元素最少的集合作为最终候选指标。若最终候选指标唯一，则确定其为最终指标集；否则选取筛选路径累积Kappa系数最大的最终候选指标集作为最终指标集。

5）输出筛选优化的最终指标集。

Kappa系数评价缩减前后指标集分区特征的一致性，改变阈值Tkappa可调节分区一致性的精度，阈值越高，分区一致性越高；FMZ修正分区过于破碎的指标集，调节破碎度阈值Tfra可调节分区完整性，阈值越低，分区相对完整性越好。

2 结果与分析

2.1 初步指标集的构建与评价

2.1.1 分区效果评价

3种方法筛选指标集的分区聚类结果评价见表1，FSCC仅在冬麦区50km和100km的效果没有优势，其他尺度下3项评价指标均显著低于两种传统方法。其中，FSCC在如皋2.5km的指标优势最为显著，其FPI、NCE、MPE值相较最大方差和拉普拉斯得分法均分别低52.44%、49.45%和49.52%，在效果不显著的冬麦区，FSCC相对最大方差法在50km处指标值最高，但FPI、NCE、MPE值仅高7.28%、7.30%和7.49%，FSCC相对拉普拉斯得分法在100km处指标值最高，但仅高8.78%、4.93%和4.96%。可见，除冬麦区50、100 km尺度，FSCC筛选指标的分区聚类表现优于2种传统方法。

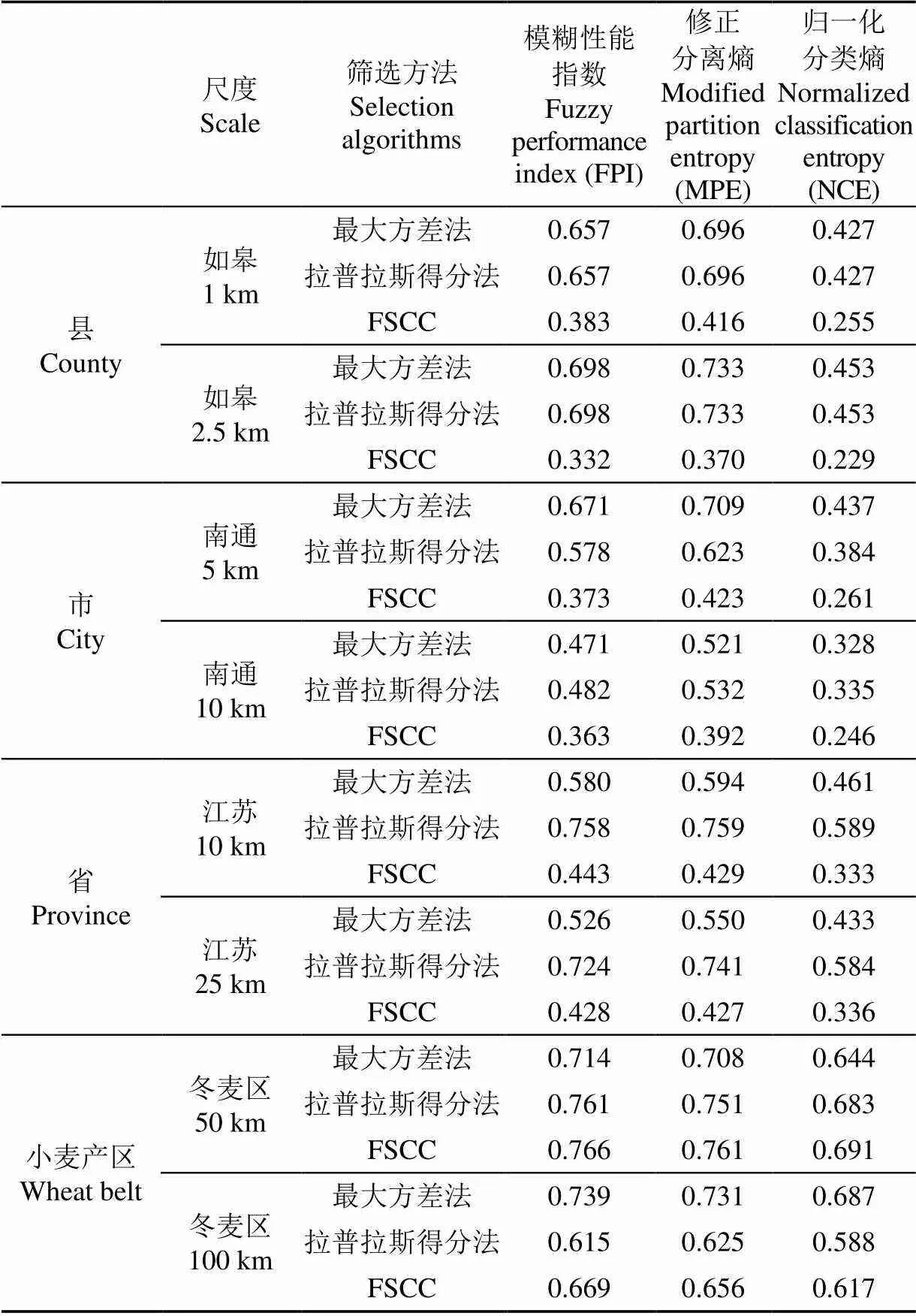
表1 3种指标筛选方法分区效果评价

2.1.2 指标集分析

3种方法各尺度下的指标筛选结果见表2：累积降水量与平均降水量、累积有效日照时长与平均气温日较差、AK与pH值、TN与OM常属同簇。平均降水量的计算基于累积降水量和当年生育期天数，相关研究显示日照与温度有一定的相关性[48]、pH值与土壤速效钾含量极显著相关[49]、土壤有机质含量与土壤总氮量间呈正相关[50]，体现FSCC对冗余环境要素有效判断、分类的能力；如皋、南通、江苏等地势低平，坡向，高程和坡度等相关性较高地形指标各分辨率下均划分为同簇，地形复杂多变的冬小麦主产区则分为不同簇，反映FSCC对地形指标的划分与区域客观地形地貌的变化相吻合。可见，FSCC从同簇高相关性指标中挑选簇中心指标，剔除冗余指标，降低了重要指标被误筛的概率，表现出具有提取表达部分指标间相关性以及指标与对应客观环境间联系的能力。

最大方差法以方差衡量指标间的离散程度，并基于方差值排序筛选指标，拉普拉斯得分法计算单一指标与剩余指标间的距离分值，并倾向于选择分值低的指标。两种方法对指标间潜在关系的忽略，易导致重要特征指标误筛和保留冗余指标的问题。4个尺度各分辨率下筛选的指标集，最大方差法几乎涵盖了方差值非常接近的坡向，高程和坡度3个地形指标，如皋、南通、江苏地形变化小，指标间高度相关，地形指标表现出自身方差值非常接近的特点，导致最大方差法未能有效剔除坡向，高程和坡度3个冗余地形指标；拉普拉斯得分法在如皋尺度各分辨率下均选择了全部地形指标、江苏与冬麦区所有分辨率下全氮与有机质同时获选、冬麦区2个分辨率下AK与pH值同时获选，李鑫等[49-50]等研究同时显示，全氮与有机质、速效钾与pH值具有冗余性，拉普拉斯法对低值指标的保留虽然筛选出与其他指标总体相关性更小、相差更大的代表指标，确无法避免保留下来的代表指标间相关性较大，冗余度高的问题。

冬麦区50和100 km尺度，最大方差与拉普拉斯法均漏选了降水指标累积降水量与平均降水量，冬麦区降水差异明显，降水指标对冬小麦生育期生长有重要影响，大尺度下剔除降水指标的合理性有待商榷。

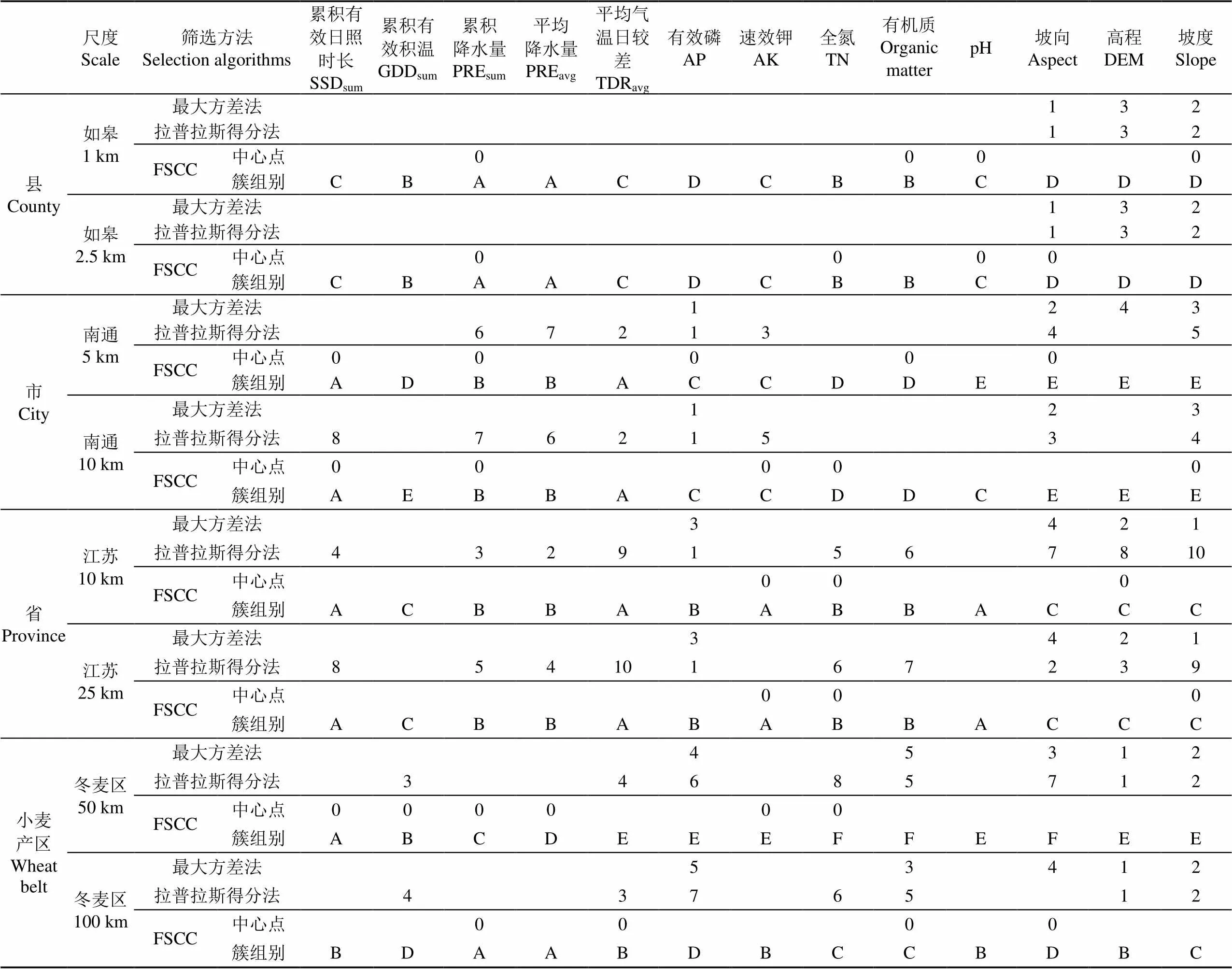
表2 指标筛选结果

注：最大方差法与拉普拉斯得分法行的数字为该列指标被选择的优先级顺序，1为最高优先级，没有数字则未被选中。FSCC行中，0代表该列指标作为中心点被选中，字母表示该列指标所属簇的组别编号。

Note: Each number in the rows of varaince and Laplacian score is the priority level of the index in this line.1 means the highest priority level and blank means the index in this line not been selected. In rows of FSCC, 0 means the index in this line is selected for being one of cluster centers, each character represents the cluster identification of the index in this line. SSD, Effective sunshine duration; GDD, effective accumulated temperature; PRE, cumulative precipitation; TDR, diurnal temperature range.

2.2 一致性与完整性优化与评价

2.2.1 分区一致性与完整性评价

FSCC及CIO筛选指标集构建的管理分区图见图1，CIO优化前如皋1 km与2.5 km、南通5 km与10 km的分区破碎明显，分区斑块多且密集，优化后的分区完整性明显提升。江苏和冬麦区2个分辨率，优化前后管理分区完整性变化不大，但在分区效果几乎保持一致基础上有效缩减了指标集，对减少指标采集工作量及后期管理分区研究具有参考意义。

尺度效应[51]是采用不同粒度、范围的数据进行分析得到的结果显著不同的现象，Jones等[52]认为多幅不同分辨率下遥感图像间不是简单的线性数学关系，而是与自然地表现状和表达目标参数的性质相关。图1可见同一研究区不同分辨率分区结果存在明显差异，与气象、土壤、地形等分区的目标表达参数在不同分辨率下的性质差异相关，表现出明显的尺度效应。

2.2.2 管理分区聚类效果评价

全指标集I1、FSCC指标集I2、CIO指标集I3的4个尺度各分辨率分区聚类效果如表3所示，除南通10 km外，I3比I2的FPI、NCE、MPE值分别平均低0.078、0.061、0.082，I2绝大部分优于全指标集I1，从模糊聚类的角度上分析，相较于其他2个指标集，CIO指标集I3具有更好的管理分区效果；南通10 km处，I3指标集相较I2，其3项指标分别略高：0.017、0.018、0.028，但二者与I1的3项指标值差距较大。分析认为分区完整性与一致性约束可能会略微影响分区的聚类表现，但提升了分区的实际可操作性。

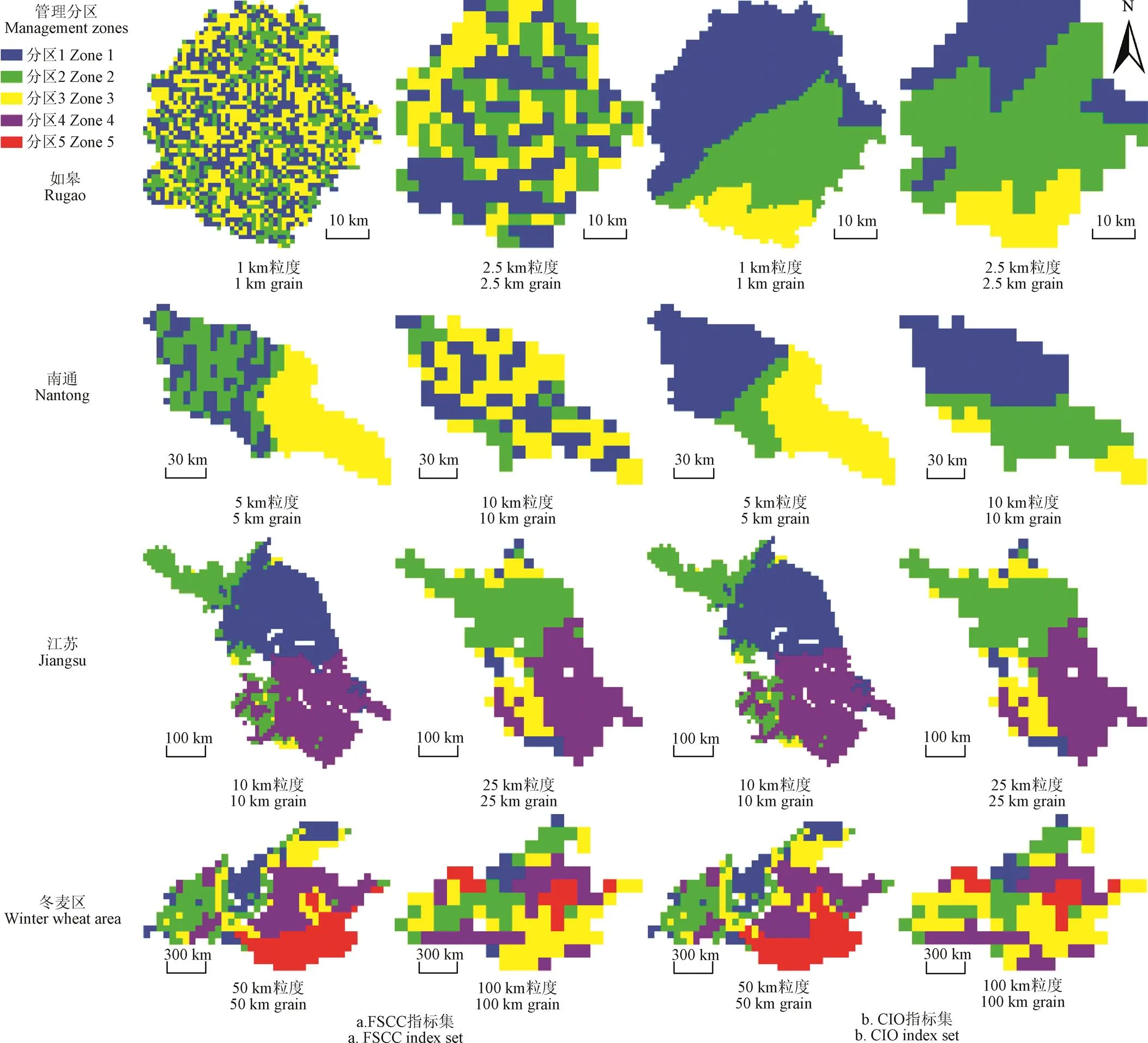
图1 优化前后分区图

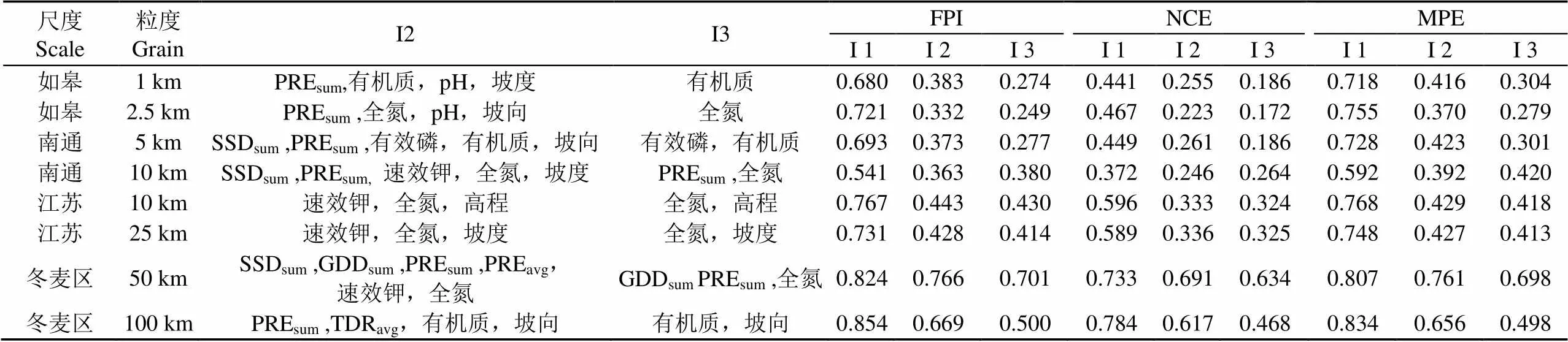
表3 指标筛选优化管理分区聚类效果评价

注：I1-全指标集，I2-FSCC指标集，I3-CIO指标集。

Note: I1-origin index set, I2-FSCC index set, I3-CIO index set.

2.2.3 CIO优化指标集结果分析

CIO优化指标集I3随尺度变化而变化（见表3），同一气候区的如皋、南通，主要分区指标为有机质、全氮、有效磷等土壤要素，随尺度增大，江苏增加了DEM等地形及降水指标，冬麦区主要因子转变为GDDsum、PREsum等气象及坡向、坡度等地形要素，气象与地形对分区的影响逐渐凸显，反映了分区指标与区域尺度的密切联系。

如皋、南通不同分辨率下，土壤指标中全氮与有机质指标相互交替出现，与该2项指标属于同簇的试验结果相契合，如皋、南通、江苏尺度的地形指标间亦如此。南通10 km包含气象指标，分析认为除尺度效应外，小气候要素的影响也可能是该类指标出现的原因之一。小气候受下垫面性质（如地形、水文、土壤、植被等）影响形成，主要表现在个别气象要素、个别天气现象的差异上，如温度、空气湿度、风、降水以及某些天气现象的分布[53]。小气候范围的垂直方向与水平方向均可从几米到数千米以上[53]。南通全境除长江边狼山一带为山丘地貌外，其余为平原，而南通10 km分区图中南通西南部分小块分区恰为边狼山一带，一定程度上反映下垫面地形要素带来的影响。

3 结 论

指标选择是管理分区研究中的重要环节，本研究针对区域尺度管理分区提出了基于相关性聚类的无监督指标筛选方法（FSSC）及基于一致性与完整性的优化方法（CIO）。对比2种传统无监督特征选择方法，FSSC具有提取表达部分指标间的相关性以及指标与对应客观环境间联系的能力，在保留原指标集内部不同特征的前提下去除冗余指标效果明显，且4个尺度各分辨率下，FSCC的聚类表现更好更稳定。针对模糊性能指数（FPI）、归一化分类熵（NCE）和修正分离熵（MPE）3个评价指标，FSCC效果平均低于最大方差法25.74%、26.01%和25.95%，平均低于拉普拉斯得分法28.41%、28.52%和28.45%，在如皋2.5km下同时低于两者52.44%、49.45%和49.52%，优势最为显著；CIO在保持分区效果一致性前提下进一步有效缩减指标集，并相对FSCC在南通10km以外尺度的FPI、NCE、MPE值上平均降低0.078、0.061、0.082，其分区指标集随尺度增大发生的变化表明CIO具有提取与区域尺度密切联系的分区指标的能力。此外，CIO在如皋、南通尺度下对导致分区破碎指标的剔除及分区完整性提升效果明显。

FSSC特征选择方法及CIO指标优化算法可为管理分区研究提供指标选择方法参考，对指标集的有效筛减可降低指标采集的资源消耗，对农作管理分区具有一定的研究意义。本文选择冬小麦产区环境特征进行了无监督分区指标筛选方法的研究，后续可结合冬小麦实际产量等指标数据，对研究方法进一步完善与优化。此外，FSSC及CIO仅能去除冗余指标及部分导致分区破碎的指标，并未有效去除与分区无关信息，如何去除无效指标也是一个值得研究的问题，不同尺度下CIO提取的分区指标集随分辨率变化各不相同，可见区域尺度变化下分区指标提取的最适分辨率问题有待进一步的研究。不同地域具有不同环境特点，本文提出的方法也需在更多不同环境地区进一步验证。

[1] Gavioli A, De Souza E G, Bazzi C L, et al. Optimization of management zone delineation by using spatial principal components[J]. Computers and Electronics in Agriculture, 2016, 127: 302－310.

[2] 王长会. 基于北斗卫星导航的大豆变量施肥技术研究与应用[D]. 长春：吉林农业大学，2016.

Wang Changhui. Research on Soybean Variable Rate Fertilization Control System and Application Based on “Beidou” Satellite Navigation System[D]. Changchun: Jilin Agricultural University, 2016. (in Chinese with English abstract)

[3] 丁海. 小麦种肥精准拟合变量施肥控制系统研发[D]. 杨凌：西北农林科技大学，2019.

Ding Hai. Research and Development of Wheat Variable Rate Fertilization Control System Based on Matching Fertilizer Line and Seed Line[D]. Yangling: Northwest A&F University, 2019. (in Chinese with English abstract)

[4] Muth D J, Bryden K M, Nelson R G. Sustainable agricultural residue removal for bioenergy: A spatially comprehensive US national assessment[J]. Applied Energy, 2013, 102: 403－417.

[5] 黄宝荣，李颖明，张惠远，等. 中国环境管理分区：方法与方案[J]. 生态学报，2010，30(20)：5601－5615.

Huang Baorong, Li Yinming, Zhang Huiyuan, et al. Environmental management regionalization in China: methods and scheme[J]. Acta Ecologica Sinica, 2010, 30(20): 5601－5615. (in Chinese with English abstract)

[6] 张天吉，余晓，诸葛亦斯. 流域环境流量管理分区方法研究：以浑河流域为例[J]. 中国水利水电科学研究院学报，2017，15(2)：116－122.

Zhang Tianji, Yu Xiao, Zhuge Yisi. Zoning methods of environmental flow management region: A case study of Hunhe River Basin[J]. Journal of China Institute of Water Resources and Hydropower Research, 2017, 15(2): 116－122. (in Chinese with English abstract)

[7] Bazzi C L, Souza E G, Uribe-Opazo M A, et al. Management zones definition using soil chemical and physical attributes in a soybean area[J]. Engenharia Agrícola, 2013, 33(5): 952－964.

[8] Schenatto K, Souza E G, Bazzi C L, et al. Data interpolation in the definition of management zones[J]. Acta Scientiarum Technology, 2016, 38(1): 31－40.

[9] Fraisse C W, Sudduth K A, Kitchen N R. Delineation of site-specific management zones by unsupervised classification of topographic attributes and soil electrical conductivity[J]. Transactions of the ASAE, 2001, 44(1): 155－166.

[10] Li Y, Shi Z, Li F, et al. Delineation of site-specific management zones using fuzzy clustering analysis in a coastal saline land[J]. Computers and Electronics in Agriculture, 2007, 56(2): 174－186.

[11] Moral F J, J M Terrón, Silva J R M D. Delineation of management zones using mobile measurements of soil apparent electrical conductivity and multivariate geostatistical techniques[J]. Soil & Tillage Research, 2010, 106(2): 335－343.

[12] Cohen S, Cohen Y, Alchanatis V, et al. Combining spectral and spatial information from aerial hyperspectral images for delineating homogenous management zones[J]. Biosystems Engineering, 2013, 114(4): 435－443.

[13] Córdoba M, Bruno C, Costa J, et al. Subfield management class delineation using cluster analysis from spatial principal components of soil variables[J]. Computers and Electronics in Agriculture, 2013, 97: 6－14.

[14] Nahuel Raúl Peraltaac, José Luis Costabc, Mónica Balzarini, et al. Delineation of management zones to improve nitrogen management of wheat[J]. Computers and Electronics in Agriculture, 2015, 110: 103－113.

[15] 周志华. 机器学习[M]. 北京：清华大学出版社，2016.

[16] 刘荣烨. 最大相关最小冗余的无监督特征选择算法的研究及其应用[D]. 青岛：中国海洋大学，2010.

Liu Rongye. Research on Application of Max-Correlation and Mix-Redundancy Unsupervised Feature Selection[D]. Qingdao: Ocean University of China, 2010. (in Chinese with English abstract)

[17] 李翔，潘瑜春，赵春江，等. 基于空间连续性聚类算法的精准农业管理分区研究[J]. 农业工程学报，2005，21(8)：78－82.

Li Xiang, Pan Yuchun, Zhao Chunjiang, et al. Delineating precision agriculture management zones based on spatial contiguous clustering algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(8): 78－82. (in Chinese with English abstract)

[18] Frey B J, Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972－976.

[19] 袁学敏. 基于模型与GIS的小麦精确栽培方案生成技术研究[D]. 南京：南京农业大学，2012.

Yuan Xuemin. Model and GIS-based on Precise Cultivation Prescription Generation Technology in Wheat[D]. Nanjing: Nanjing Agricultural University, 2012. (in Chinese with English abstract)

[20] 童倩倩，李莉婕，赵泽英，等. 基于GIS的贵州稻田土壤养分管理分区[J]. 西南农业学报，2017，30(12)：2727－2731.

Tong Qianqian, Li Lijie, Zhao Zeying, et al. Management subarea of paddy soil nutrients based on GIS in Guizhou[J]. Southwest China Journal of Agricultural Sciences, 2017, 30(12): 2727－2731. (in Chinese with English abstract)

[21] 李朋彦，常栋，王莹，等. 基于GreenSeeker的烟田管理分区研究[J]. 中国烟草学报，2015，21(6)：96－102.

Li Pengyan, Chang Dong, Wang Ying, et al. Demarcating tobacco field management based on GreenSeeker[J]. Acta Tabacaria Sinica, 2015, 21(6): 96－102. (in Chinese with English abstract)

[22] 郭澎涛，李茂芬，罗微，等. 基于土壤属性和环境变量的橡胶园管理分区[J]. 南方农业学报，2015，46(10)：1839－1848.

Guo Pengtao, Li Maofen, Luo Wei, et al. Management zones of rubber plantation based on soil properties and multi-sourced environmental variables[J]. Journal of Southern Agriculture, 2015, 46(10): 1839－1848. (in Chinese with English abstract)

[23] 管青春，郝晋珉，许月卿，等. 基于生态系统服务供需关系的农业生态管理分区[J]. 资源科学，2019，41(7)：1359－1373.

Guan Qingchun, Hao Jinmin, Xu Yueqing, et al. Zoning of agroecological management based on the relationship between supply and demand of ecosystem services[J]. Resources Science, 2019, 41(7): 1359－1373. (in Chinese with English abstract)

[24] 施建平，宋歌. 基于Web的中国土种数据库[J]. 土壤，2016，48(6)：1246－1252.

Shi Jianping, Song Ge. Web based soil type database of China[J]. Soils, 2016, 48(6): 1246－1252. (in Chinese with English abstract)

[25] Doerge T A. Management zone concept in Site-specific management guidelines[Z]. Potash&Phosphate, Institute, Norcross, 2000.

[26] 徐英，陈亚新，史海滨，等. 土壤水盐空间变异尺度效应的研究[J]. 农业工程学报，2004，20(2)：1－5.

Xu Ying, Chen Yaxin, Shi Haibin, et al. Scale effect of spatial variability of soil water-salt[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(2): 1－5. (in Chinese with English abstract)

[27] 邬建国. 景观生态学格局、过程、尺度与等级（第二版）[M]. 北京：高等教育出版社，2007.

[28] 李双成，蔡运龙. 地理尺度转换若干问题的初步探讨[J].地理研究，2005，24(1)：11－18.

Li Shuangcheng, Cai Yunlong. Some scaling issues of geography[J]. Geographical Research, 2005, 24(1): 11－18. (in Chinese with English abstract)

[29] Krige D G. A Statistical Approach to Some Mine Valuation and Allied Problems on the Witwatersrand[D]. Johannesburg: University of the Witwatersrand, 1951.

[30] 瞿明凯. 几种地统计学方法在县域土壤空间信息处理上的应用与研究[D]. 武汉：华中农业大学，2012.

Qu Mingkai. Application and Study of Several Geostatistical Methods in Soil Spatial Information Processing at County Scale[D]. Wuhan: Huazhong Agricultural University, 2012. (in Chinese with English abstract)

[31] 冯益明. 空间统计学理论及其在林业中的应用[M]. 北京：中国林业出版社，2008.

[32] 钱永兰，吕厚荃，张艳红. 基于ANUSPLIN软件的逐日气象要素插值方法应用与评估[J]. 气象与环境学报，2010，26(2)：7－15.

Qian Yonglan, Lü Houquan, Zhang Yanhong. Application and assessment of spatial interpolation method on daily meteorological elements based on ANUSPLIN software[J]. Journal of Meteorology and Environment, 2010, 26(2): 7－15. (in Chinese with English abstract)

[33] 刘志红，Mcvicar T R，Niel V，等. 专用气候数据空间插值软件ANUSPLIN及其应用[J]. 气象，2008，34(2)：92－100.

Liu Zhihong, Mcvicar T R, Niel V, et al. Introduction of the professional interpolation software for meteorology data: ANUSPLINN[J]. Meteorological Monthly, 2008, 34(2): 92－100. (in Chinese with English abstract)

[34] 董玮，陈桂芬. 精准农业中管理区划分方法研究[J]. 安徽农业科学，2011，39(17)：10685－10687.

Dong Wei, Chen Guifen. Study on the management division methods in precision agriculture[J]. Journal of Anhui Agricultural Sciences, 2011, 39(17): 10685－10687. (in Chinese with English abstract)

[35] Gorsevski P V, Gessler P E, Jankowski P. Integrating a fuzzy k-means classification and a Bayesian approach for spatial prediction of landslide hazard[J]. Journal of Geographical Systems, 2003, 5(3): 223－251.

[36] Lark R M, Stafford J V. Classification as a first step in the interpretation of temporal and spatial variation of crop yield[J]. Annals of Applied Biology, 1997, 130(1): 111－121.

[37] Odeh I O A, Chittleborough D J, Mcbratney A B. Soil pattern recognition with fuzzy-c-means: Application to classification and soil-landform interrelationships[J]. Soil Science Society of America Journal, 1992, 56(2): 505.

[38] 岳瑞红. 基于MODIS数据的蒙古高原土地覆盖分类研究[D]. 呼和浩特：内蒙古师范大学，2010.

Yue Ruihong, Research on land cover classification in Mongolian Plateau based on MODIS data[D]. Huhhot: Inner Mongolia Normal University, 2010. (in Chinese with English abstract)

[39] Monserud R A, Leemans R. Comparing global vegetation maps with the Kappa statistic[J]. Ecological Modelling, 1992, 62(4): 275－293.

[40] 布仁仓，常禹，胡远满，等. 基于Kappa系数的景观变化测度：以辽宁省中部城市群为例[J]. 生态学报，2003，25(4)：778－784.

Bu Rencang, Chan Yu, Hu Yuanman, et al. Measuring spatial information changes using Kappa coefficients: A case study of the city groups in central Liaoning Province[J]. Acta Ecologica Sinica, 2003, 25(4): 778－784. (in Chinese with English abstract)

[41] 傅伯杰. 景观生态学原理及应用（第二版）[M]. 北京：科学出版社，2011.

[42] 王云才. 基于景观破碎度分析的传统地域文化景观保护模式：以浙江诸暨市直埠镇为例[J]. 地理研究，2011，30(1)：10－22.

Wang Yuncai. The models of traditional culture landscape conservation based on landscape fragmentation analysis: A case study of Zhibuzhen in Zhejiang Province[J]. Geographical Research, 2011, 30(1): 10－22. (in Chinese with English abstract)

[43] He X, Cai D, Niyogi P. Laplacian score for feature selection[C]//International Conference on Neural Information Processing Systems, MIT Press, 2005.

[44] 郭澎涛，李茂芬，林钊沐，等. 基于多源环境变量的橡胶园土壤管理分区[J]. 农业工程学报，2014，30(12)：96－104.

Guo Pengtao, Li Maofen, Lin Zhaomu, et al. Delineating soil management zones in rubber plantation using multisource data of environmental variables[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(12): 96－104. (in Chinese with English abstract)

[45] 张国祥，杨居荣. 综合指数评价法的指标重叠性与独立性研究[J]. 农业环境保护，1996(5)：213－217.

[46] Fisher R A. Statistical Methods, Experimental Design, and Scientific Inference[M]. New York: Oxford University-Press, 1990.

[47] 董俊，王锁萍，熊范纶. 可变相似性度量的近邻传播聚类[J]. 电子与信息学报，2010，32(3)：509－514.

Dong Jun, Wang Suoping, Xiong Fanlun. Affinity propagation clustering based on variable-similarity measure[J]. Journal of Electronics & Information Technology, 2010, 32(3): 509－514. (in Chinese with English abstract)

[48] 曾昭美，严中伟. 近40年我国云、日照、温度及日较差的统计[J]. 科学通报，1993，38(5)：440—443.

[49] 李鑫. 土壤pH值与养分肥力指标的相关性分析[J]. 安徽农学通报，2017(21)：73－74.

[50] 王莹. 土壤有机质与氮磷钾的相关性[J]. 农业科技与信息，2008(17)：32－33.

[51] 谭诗腾. 基于斑块形态的类别栅格数据聚合尺度效应模型构建[D]. 成都：西南交通大学，2018.

Tan Shiteng. Morphology-based Modeling of Aggregation Effect on the Categorical Raster Data[D]. Chengdu: Southwest Jiaotong University, 2018. (in Chinese with English abstract)

[52] Jones H G, Sirault X R R. Scaling of thermal images at different spatial resolution: The mixed pixel problem[J]. Agronomy, 2014, 4(3): 380－396.

[53] 黄寿波. 农业小气候学[M]. 杭州：浙江大学出版社，2000.

Unsupervised feature selection and fragmentation optimization of agriculture management zones at a regional scale

Huang Fen1,2, Zhu Jincheng1, Zhang Xiaohu2, Liu Tongyu1, Zhu Yan2

(1.,,210095,; 2.,,210095,)

Dividing farmland into different zones for facilitating management (management zone) at regional scalescan help improve agricultural production in reforming agricultural technology implementation in China. Improving detailed prescriptionof the management zone division can provide guidance to farming and service optimization at regional scale.Appropriately selecting indexes in management zones can reduce the required data and can thus subsequentlyimprove management.Available index selection usually relies on empirical knowledge of expertsand/or multivariate statistical analysis. However, expert evaluation method could be bias, while the multivariate statistical analysis methodcannot reduce the number of indexes compared to the original index set and thus need to supervisethe data. In addition, most existing work on fragmentation of management zones focused on zone-dividing method rather than from index selection by removing indexes that lead to fragmentation. This paper aims to resolve these limitations with a proposedunsupervised filtering index selection method, based on the index correlation clustering (FSCC) using the concept of feature selection. FSCC reduces the original index set to obtain a subset called FSCC set. FSCC applies the correlation matrix of all indexes to cluster the original indexes set. It then selectsall cluster centers as a representatives to form a new index subset as theFSCC set. The quantity of the indexes in the FSCC setwas reduced,compared to the original index set, and the redundancy of the indices set was descended. To improve practical operability of the management zones, we applied the index optimization algorithm developed based on the consistency and integrity (CIO) to the FSCC set to remove indices which resulted in fragmentation. CIO couples Kappa Coefficient with fragmentation index to generate an optimization strategy for the FSCC sets. CIO screens the indices which lead to the fragmentationwhile, in the meantime, considering the consistency of the management zone results prior to and after the optimization. We applied the method to winter wheat in China, with factors that affect wheat growth, including meteorology, soil and topography, being dividedat fourregional scales. We first usedthe FSCC and the two traditional filter feature selection methods, Variance and Laplacian Score, to select index subsets for thefour scales, and compared the resultant management zones produced from them. The CIO was then applied to the four scales produced by the FSCC. The results showed that the FSCC method preserves the diversity of the features in the original index set. It significantly removed the redundant indices and had a better performance in the management zones. The best performance shows that in Rugao 2.5 km Grain, FSCC less than 52.44%, 49.52%, 49.45% both of Variance and Laplacian Score in FPI, MPE, NCE. The CIO improved the management zones effect of the FSCC index set, which reduced the number of indexes and effectively removed the indexes that led to anumber of isolated units or patches. Compare to FSCC, except Nantong 10km, CIO has an average decrease in FPI, MPE, NCE of 0.061, 0.078, 0.082. Usingthe fourregional scales, FSCC and CIO presented in this paper were effectivein selecting indices and havepotentialapplication in management zone division.

agriculture; management zone; algorithm; feature selection; filter; consistency and integrity optimization; reginal scale

2019-09-20

2019-12-16

国家重点研发项目（2016YFD0300607）

黄 芬，博士，副教授，研究方向为人工智能与大数据分析、图像处理。Email：fenhuang@njau.edu.cn

10.11975/j.issn.1002-6819.2020.05.022

S126; TP391.4

A

1002-6819(2020)-05-0192-09

黄 芬，朱金诚，张小虎，刘通宇，朱 艳. 区域尺度农业管理分区的无监督特征选择与破碎度优化算法[J]. 农业工程学报，2020，36(5)：192－200. doi：10.11975/j.issn.1002-6819.2020.05.022 http://www.tcsae.org

Huang Fen, Zhu Jincheng, Zhang Xiaohu, Liu Tongyu, Zhu Yan. Unsupervised feature selection and fragmentation optimization of agriculture management zones at a regional scale[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(5): 192－200. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.05.022 http://www.tcsae.org