基于特征价格模型的昆明市商品房住宅价格影响因素研究

杨 鑫

(云南财经大学 云南 昆明 650032)

进入21世纪以来，中国的住宅价格就随着中国的经济增长也在快速的增长着，快速增长的房价也引起了各界的广泛关注，许多学者都在尝试用各种不同的方法来去寻找影响房价的因素，近几年来使用最广泛方法包括通过GIS、空间计量模型、特征价格模型等，笔者选择的方法是建立特征价格模型。

一、研究区概况

昆明市是云南省的省会城市、滇中城市群中心城市，国务院批复确定的中国西部地区重要的中心城市之一，又名“春城”。截止到2019年底，全市下辖7各区、3个县、代管1个县级市和3个自治县，总面积21473平方千米，建成区面积435.81平方千米，与2018年相比，2019年昆明市常住人口667.7万人，增长1.7%；全市地区生产总值6400亿元，增长7.5%；全年商品房销售额1570万元，增长20.24%；全年城镇居民人均可支配收入22049元，增长8%。选取昆明市五华区、盘龙区、西山区、官渡区为研究范围，以2019年1—4月主城区新开盘或在售的楼盘为研究对象．通过咨询相关专家和实际调研，选取500个楼盘样本点，以保证样本点的科学性和典型性．

二、研究方法与数据来源

(一)研究方法

特征价格理论提出较早，之后依次经历了沉寂、快速发展时期，直到如今的普遍应用的现状。在其快速发展阶段，出现了两位重要人物Lancaster 和Rosen，这么多年来大多数研究者都是Rosen 的建议中选择函数，Rosen 建议可采取的函数形式有：线性函数、对数函数、半对数函数、双对数函数等，后来又有研究者提出了Box-Cox 变换函数。这些函数形式本身并没有优劣之分，它们的优劣只是体现在对同一组样本数据进行拟合分析时所表现出来的效果差异。特征价格模型的原理是，在竞争机制作用下市场均衡时消费者想购买某一商品，而该商品具有很多特征，用X1，X2，X3，……Xn来表示，消费者愿意为这些特征所花的价钱总和P 为该商品的特征价格，此特征价格P为特征用X1，X2，X3，……Xn的一个函数，即：

P=f(X1,X2,X,…Xn)

对于上式关于特征变量Xi求偏导，得到 就是特征Xi的隐含价格。

1.变量的选择

特征价格模型因变量通常指一套住宅总价格，自变量是指住宅所包含的特征变量。住宅房产的价格随房屋特征改变和时间变化而产生价格变动。在特征价格模型中，参入拟合的房产交易时间相近，所以主要考虑房产价格随房屋住宅特征改变而引起的价格变动。在对国内外学者的相关文献的研究中，将住宅的特征分为建筑特征、邻里特征以及区位特征三大类，建筑特征大多采用绿化率、容积率、物业管理费等，邻里特征大多采用到商业中心的距离、自然景观、教育配套、医疗配套等；区位特征大多采用公路线路数、交通主干道等级、所在行政区域等变量。笔者结合昆明市的实际情况，将特征因素分为3大类、17个具体特征变量，其中选取住宅租金内建筑特征为：建筑面积、房龄、朝向状态、装修程度、所在楼层、房间数目、房屋配套7个因素，选取邻里特征为：到最近中学距离、到最近小学距离、到最近幼儿园距离、到最近公园距离、到最近汽车站距离、到最近农贸市场距离、到最近医院距离以及到最近主干道距离8个因素，选取区位特征为：到市中心的距离、到最近商圈的距离2个因素，研究其对昆明市住宅租金均价的影响程度。住宅特征变量及含义见表1。

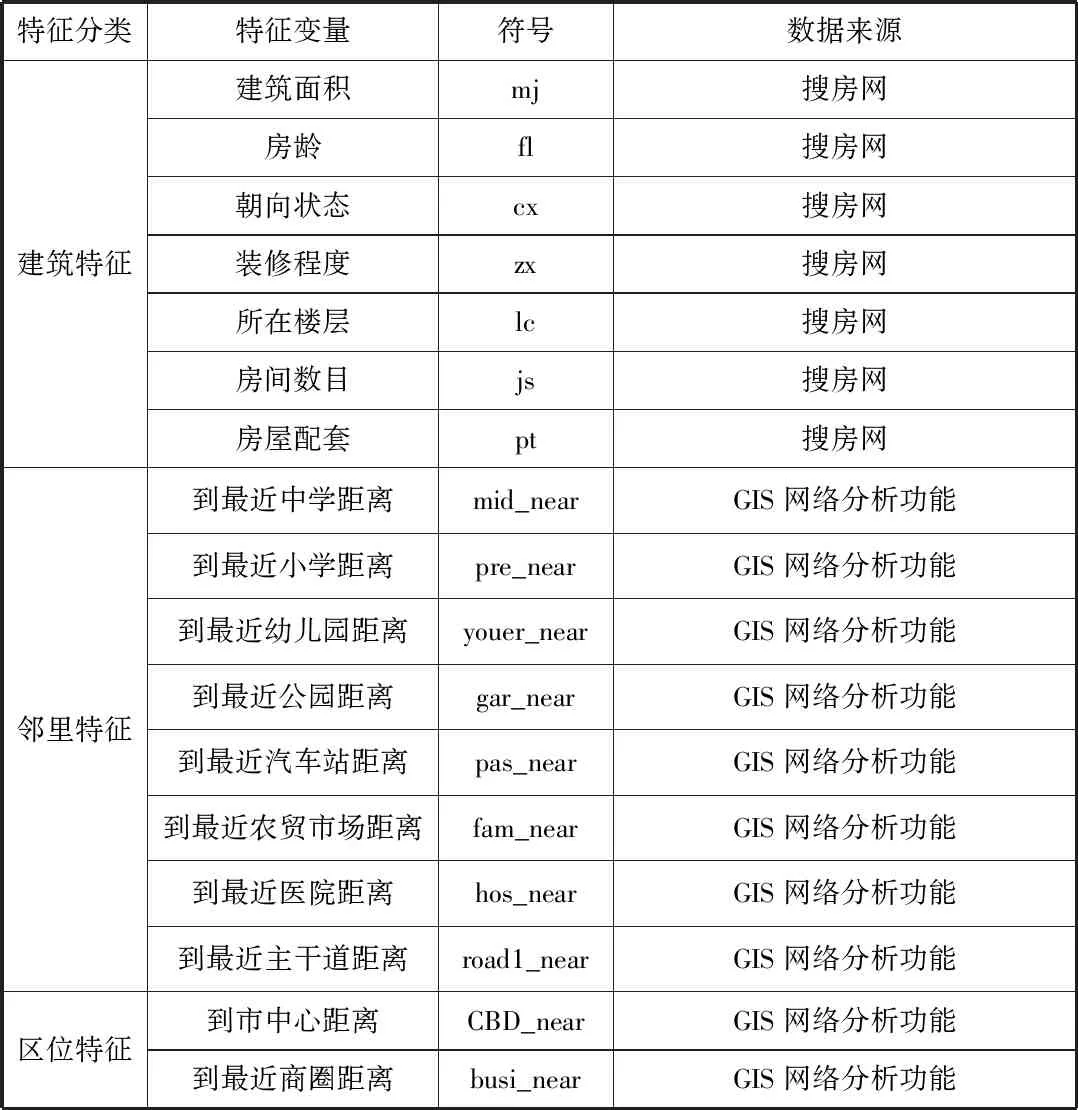
表1 住宅特征变量及来源

2.变量的量化

(1)特征变量的线性量化

整理之后的租赁住宅变量共计17个，不同种类的变量需要采用不同的方式进行量化，参考国内外优秀的文献，本文采用的线性量化方式可以分为四类：一是直接采用原始数据作为变量值；二是用5点Likert量表的形式对变量进行分级，采用分级后的指标；三是采用综合性指标度量作为应用数据；四是采用GIS 辅助特征变量的量化。对建筑面积、房龄、所在楼层、房间数目采用实际观测数据进行线性量化，对装修程度采用5点Likert量表进行分级，对朝向、房间配套进行综合性指标度量；到最近中学距离、到最近小学距离、到最近幼儿园距离、到最近公园距离、到最近汽车站距离、到最近农贸市场距离、到最近医院距离以、到最近主干道距离、到市中心的距离以及到最近商圈的距离利用GIS的网络分析功能得到欧式距离。

根据上面四种量化方式，整合后得到的总的特征变量的线性量化如下表2所示：

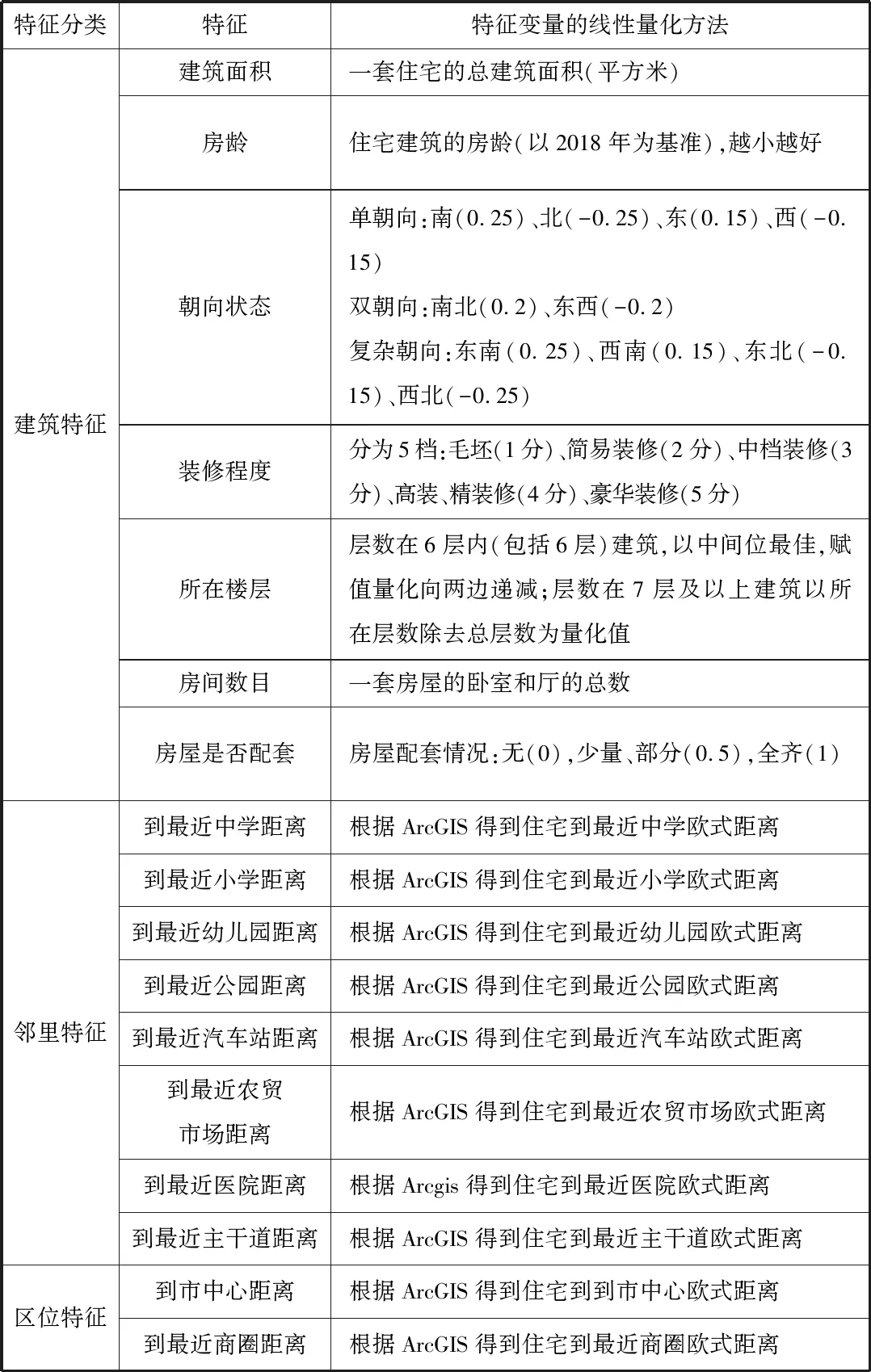
表2 特征变量线性量化表

(2)特征变量的对数量化

根据上面四种量化方式，以及参考《城市住房子市场的Hedonic分析-以重庆市为例》和《城市住宅的特征价格_理论分析与实证研究》等文献，对特征变量进行对数量化，整合后得到的总的特征变量的对数量化如下表3所示：

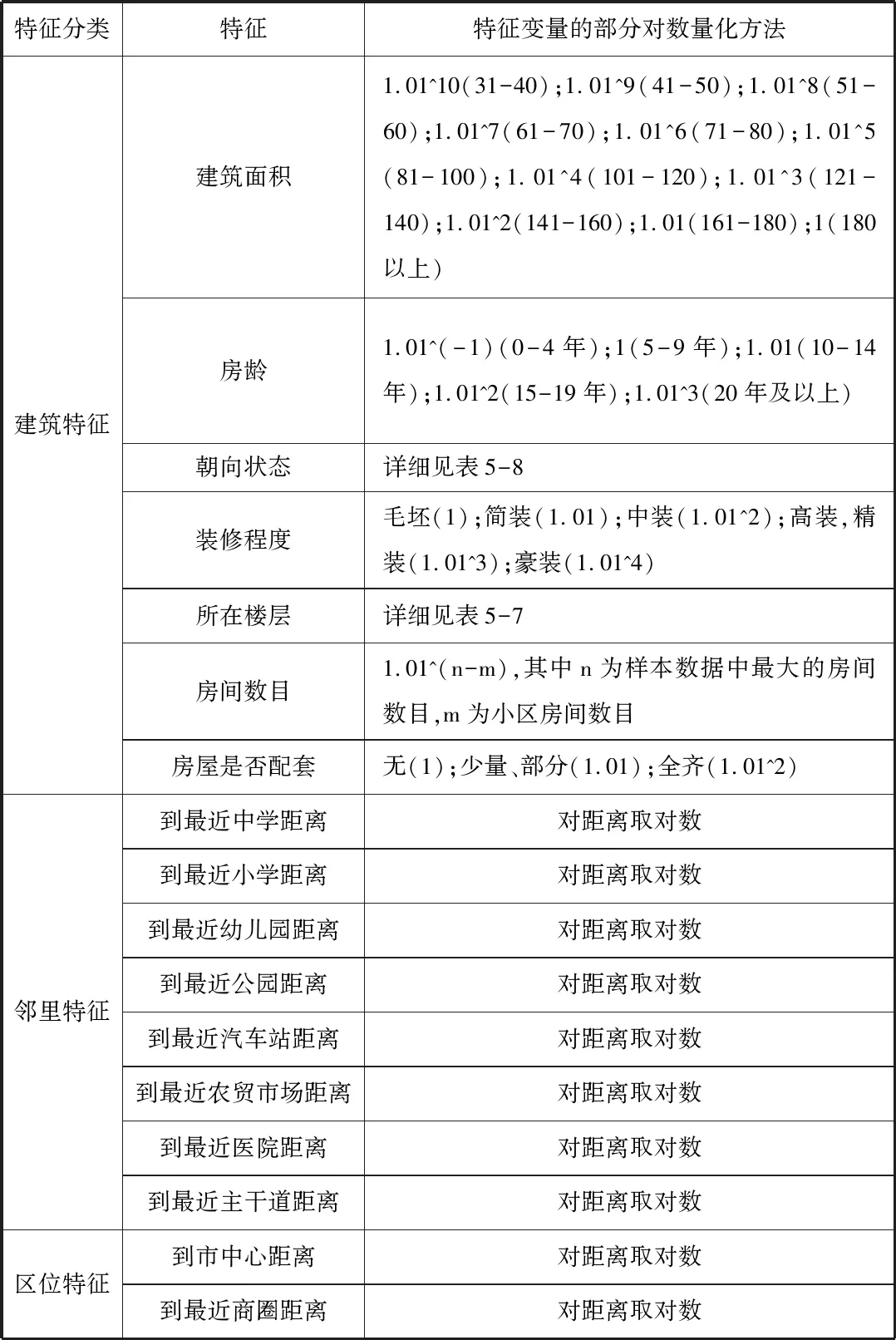
表3 特征变量对数量化表

3.模型的函数形式及选择

根据Rosen 的经验推导方法，我们知道特征价格模型的形式主要包括四种：线性模型、对数模型、半对数模型以及对数线性模型，本研究采用线性函数形式和双对数函数形式构建城市住宅租金特征价格模型，其基本模型分别为：

(1)线性函数模型

P=α0+∑αiZi+ε

(式5-17)

其中：P为城市住宅平均租金价格(元/平方米)，Zi为城市住宅租金价格影响因素量化数值，α0，αi为待定系数，ε为随机误差项；

(2)对数模型

lnP=α0+∑αilnZi+ε

(式5-18)

其中：P为城市住宅平均租金价格(元/平方米)，Zi为城市住宅租金价格影响因素量化数值，α0，αi为待定系数，ε为随机误差项；

(二)数据来源

特征价格模型所用的数据是由搜房网中介网站提供的2019年1-4月昆明市主城区房屋内部因素相对较全的交易案例数据1250套，以及通过GIS的网络分析功能得到的住宅邻里特征和区位特征的欧氏距离，踢出内部因素缺失较大、以及异常交易数据后，最终有1172个交易案例数据运用到该模型。

三、实证研究

(一)模型的设定

选用SPSS20.0和Excel2010软件作为资料整理和分析工具，由它们来完成模型的描述性统计分析、模型选优以及各变量的统计显著性检验等技术性工作。分别将因变量即住宅小区均价、17个自变量代入特征价格线性函数和对数函数模型中，进行回归分析。

(二)模型的估计和检验

1.模型的估计与检验

在SPSS20.0中用最小二乘法对特征价格面模型进行估计，对样本数据进行回归(置信区间为95%)，得到回归分析表,对其进行异方差检验，发现有异方差，会影响模型拟合结果；然后对其进行异方差处理，用模型拟合的残差对原模型进行加权，采用线性函数模型和对数函数模型加权后的回归结果如下表4和表5所示：

表4 线性函数模型回归模型

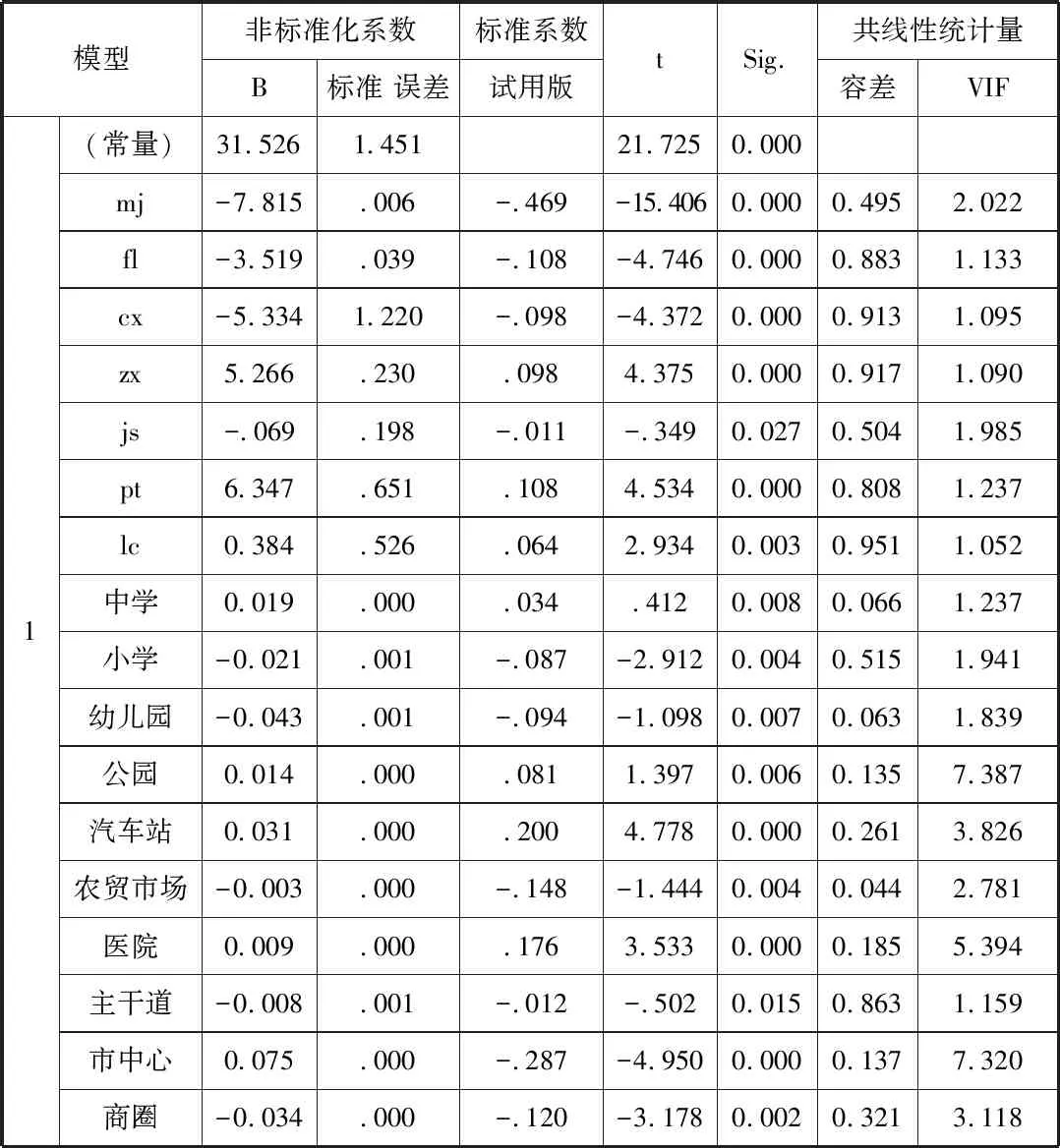
表5 线性函数模型回归系数分析

表6 对数函数回归模型

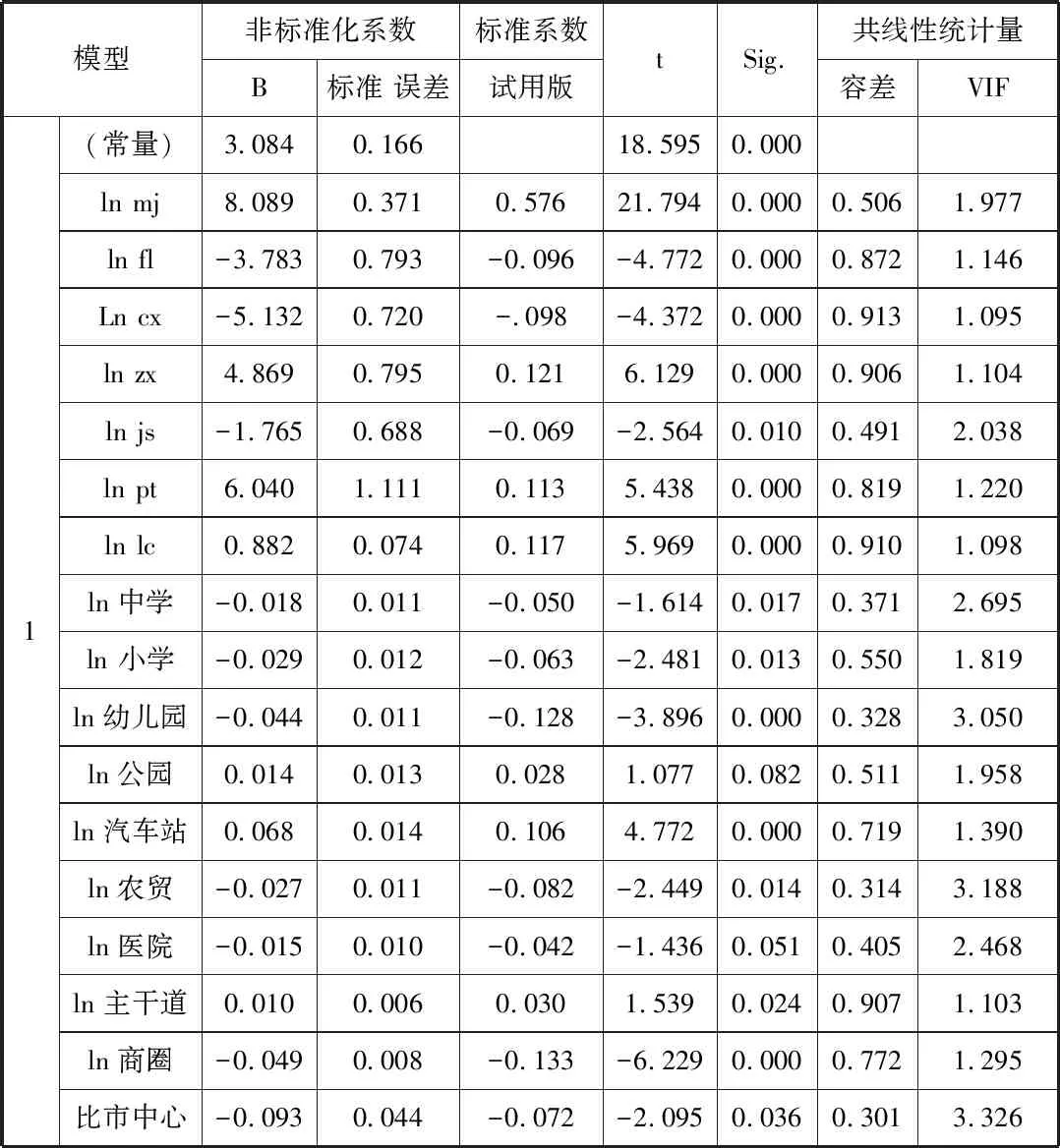
表7 对数函数模型回归系数分析

一般来讲，复相关系数取值在区间[0，0.09]内，表明没有相关性；在区间[0.1，0.3]内，表明为弱相关；在区间[0.3，0.5]内，表明为中度相关；在区间[0.5，1.0]内，表明为强相关。由表5-10和表5-12可知，这两种函数模型的复相关系数均大于0.5，表明两种模型的均价与其他自变量线性关系较强。另外，方差分析表中显示了显著性检验值Sig.均为0.000，小于0.001，说明了四种模型均拒绝了认为全部特征变量系数为0 的原假设，表明四种模型的回归方程中因变量与自变量的关系能成立。

判定系数R2和调整后的R2是反映模型拟合效果的指标，发现对数模型的判定系数和调整后的判定系数值最高，并且方差分析表中对数函数模型的F 值也大于其他模型，说明对于本文的样本数据，对数函数模型在上述两种模型中拟合度较好，还需要进行其他方面的检验，来确定其是否在两种模型中最佳。

从表中看出，两种模型的VIF 值最大值分别为7.387、3.050，因此各自变量的VIF 值均小于10，所以各特征变量的共线性关系不显著。对数模型的容差的均值为0.963，大于比线性模型的容差均值0.831，对数模型的VIF的均值为1.039，小于线性模型的VIF1.274，说明全对数模型在多重共线性问题上比线性模型更优，所以选择全对数模型进行相关系数的修正。

(三)模型的结果

线性函数特征价格模型

由上表5可知，最近商圈的距离、到市中心的距离、朝向状态、到最近农贸市场的距离、房龄、到最近公园距离、到最近医院距离、所在楼层、到最近中学的距离、建筑面积、到最近小学距离、房屋配套、到最近主干道距离、到最近幼儿园距离、装修程度共15个租金影响因素进入模型，且对模型进行异方差和线性相关性检验，都通过了检验，说明它们是影响昆明市住宅用地价格的主要影响因素。按回归结果并将房租均价设为P，则昆明市住宅租金价格Hedonic模型可以表述为：

P = 31.53-3.4*BUSI_NEAR-7.5*CBD_NEAR +5.33*CX-0.3FAM_NEAR-3.5*FL-1.4*GAR_NEAR-0.9*HOS_NEAR +0.38*LC-1.9*MID_NEAR-7.8*MJ-2.1*PRE_NEAR + 6.34*PT-0.8*ROAD1_NEAR-4.3*YOUER_NEAR +5.26*ZX+3.1*BAS_NEAR

(模型1)

对数函数特征价格模型

从表7可以看出，到最近商圈的距离、到市中心的距离、朝向状态、到最近农贸市场的距离、房龄、到最近公园距离、到最近医院距离、所在楼层、到最近中学的距离、建筑面积、到最近小学距离、房屋配套、到最近主干道距离、到最近幼儿园距离、装修程度共15个租金影响因素进入模型,且对模型进行异方差和线性相关性检验，都通过了检验，说明它们是影响昆明市住宅用地价格的主要影响因素。则昆明市住宅租金价格Hedonic模型可以表述为：

Ln(P)= 3.08 4-0.049*Ln(BUSI_NEAR)+0.85*LN(CX)-0.027LN(FAM_NEAR)-3.78*LN(FL)-0.014*Ln(GAR_NEAR)-0.015*Ln(HOS_NEAR)+0.882*LN(LC)-0.018*Ln(MID_NEAR)+8.089*Ln(MJ)-0.029*Ln(PRE_NEAR)+6.04*LN(PT)-0.010*Ln(ROAD1_NEAR)-0.044*Ln(YOUER_NEAR)+ 4.869*Ln(ZX)-0.93*CBD_NEAR

(模型2)

从标准化模型5-2中的各个自变量前面的系数可以看出，即自变量对数量化单位每提高一个等级。如对于到商圈距离这一影响因素，到最近商圈越近，则让昆明市住宅租金增加了4.9%，以后依次为到市中心距离(9.3%)、朝向(0.85%)、到最近农贸市场距离(2.7%)、房龄(3.78%)、到最近公园距离(1.4%)、到最近医院距离(1.5%)、楼层(0.882%)、到最近中学的距离(1.8%)、建筑面积(8.0%)、到最近小学距离(2.9%)、房屋配套(6.04%)、到最近主干道距离(1%)、到最近幼儿园的距离(4.40%)、房屋装修(4.87%)。

特征价格的符号和系数:

模型1和模型2中的各个自变量前面的系数和符号，代表了昆明市住宅租金价格影响因素的特征价格。在5%的显著性水平下，符号为正表示自变量每增加一个单位，因变量就增加相应系数数值的数量；同理符号为负时表示自变量每增加一个单位，因变量就减少相应系数数值的数量。如模型2中对于装修这一影响因素，装修从毛坯到豪装的差别，则让昆明市住宅租金增加了4.869元/平方米。

四、结论与讨论

由实证检验的模型1和模型2对比中可以看出对数特征价格模型具有更好的说明性，在模型2中，面积、配套设施、装修、房龄、到市中心距离、楼层、朝向都对住宅价格有非常显著性的影响，其中房龄和到市中心距离与与住宅价格的关系具有负相关性，房龄越久、到市中心越远，住宅均价越低；面积、配套设施、装修、楼层、朝向均呈现正相关性，面积越大、装修设施越齐全住宅均价越高，因为楼层采用模糊数学法进行量化，越靠近中间的楼层量化值越大，即越靠近中间的楼层住宅均价越高。

由于使用方法较为单一，没有使用多种研究方法结合的方式，仅用特征价格模型对因变量和自变量进行解释，是结果可能存在部分偏差，同时没有对变量的时间因素进行深化研究，这些都有待于进行更为深入的研究。