基于非线性Granger因果检验的黄金量化分析
2020-04-23晏海青陈雪东
晏海青, 陈雪东
(1.浙江师范大学 数学与计算机科学学院, 浙江 金华 321004; 2.湖州师范学院 理学院, 浙江 湖州 313000)
0 引 言
近年来经济全球化进程不断加快,对国际黄金变化的影响与日俱增,黄金价格变化在全球经济中的影响和作用越来越重要.虽然目前对于黄金方面的研究非常多,但大都属于定性或基于线性的定量研究.而实际上黄金价格的变化多数是非线性的.本文重点考虑非线性Granger因果检验对黄金价格变化的相关研究.
经典的Granger因果检验是由C W J Granger(1969)[1]提出的,其推动了计量经济学的发展.大部分研究依赖于传统的线性格兰杰因果关系检验,但传统的Granger因果检验存在很大的局限性.对此,经济学家相继对Granger因果检验作出创新:Baeck和Brock(1992)[2]提出了非线性Granger因果检验,但其预测能力较低;Hiemstra 和Jones[3]在Baeck和Brock基础上对非线性Granger因果检验作出改进,并用此研究股票价格与交易量之间的关系;Toda和Yamamoto(1995)[4]提出的Wald检验分析了非线性Granger因果关系,是一个具有代表性的Granger因果检验;Diks和Panchenko(2006)[5]在后续研究中发现,Hiemstra和Jones提出的检验存在过度排斥,故提出了最新的Granger因果检验.根据目前的研究现状,本文结合非线性Granger因果检验对黄金进行定量分析,以期对黄金价格变化作出正确的预测.
1 理论基础与方法步骤
1.1 非线性Granger因果检验
Granger(1969)[1]提出的Granger因果检验在经济学中的应用十分广泛,是现代计量经济学检验因果关系的重要分析方法.该方法检验严格平稳的双变量时间序列{Xt,Yt,t≥1},如果Xt对Yt的预测有解释作用,则称Xt是Yt的Granger原因;如果Yt对Xt的预测有解释作用,则称Yt是Xt的Granger原因.即
(1)
(2)
其中,ε1t、ε2t是两个不相关的白噪声序列.由上述因果关系定义,当给定某个不为0的bi时,Yt是导致Xt的Granger原因;当给定某个不为0的ci时,Xt是导致Yt的Granger原因.
经典的Granger是用受约束的F检验完成的,假设Xt不是导致Yt的Granger原因,即上述定义(2)式的Xt滞后项参数为零,分别做包含Xt滞后项的回归和不包含滞后项的回归,记前者的残差平方和为RSS1,后者的残差平方和为RSS2,得到F检验统计量:
(3)
其中,n为Xt的滞后项个数,m为样本容量,k为包含可能存在的常数项以及其他变量和无约束回归模型的待估参数个数.若计算出的F值大于给定的显著性水平α,则拒绝原假设,认为Xt是导致Yt的Granger原因.
随着计量经济学的快速发展,非线性研究领域受到人们越来越多的关注.但研究发现,对于非线性的时间序列,经典Granger因果检验无法正确检验出非线性的因果关系.如果一味使用经典的Granger因果检验将会得到虚假的因果关系,结论也将出现偏差.为了克服经典的Granger因果检验带来的问题,本文使用Toda和Yamamoto(1995)[4]提出的非线性Granger因果关系-Wald检验.近年来其在Granger因果检验中应用广泛,用以检验变量之间线性和非线性的因果关系.最典型的就是将Wald检验用在向量自回归(VAR)模型中,估计模型系数的线性和非线性限制.
1.2 基于Wald检验的步骤
yt=β0+β1t+…+βqtq+ηt,
(4)
其中,{ηt}是d阶差分后平稳序列,且ηt=J1ηt-1+…+Jkηt-k+εt.假设k已知,{εt}是独立同分布的n维随机向量,E(εt)=0,协方差矩阵∑ε>0.
然后,令ηt=yt-β0-β1t-…-βqtq,可以得到:
yt=γ0+γ1t+…+γqtq+J1yt-1+…+Jkyt-k+εt,
(5)
其中,γi(i=1,…,q)是βi(i=0,…,q)和Jh(h=1,…,k)的函数.
在这种情况下,非线性Granger因果检验的原假设为:
H0:f(φ)=0.
(6)
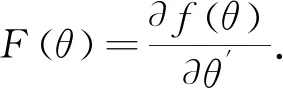
为检验假设(6),考虑估计VAR模型:
(7)
其中,t=1,…,T,p≥k+d.为了更好地估计,将(7)式写成:
(8)
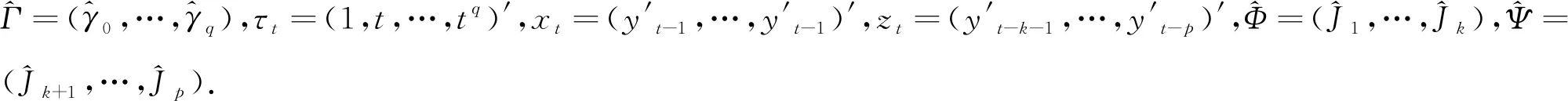
(9)
其中,Τ′=(τ1,…,τT)′,Χ′=(x1,…,xT)′.

(10)
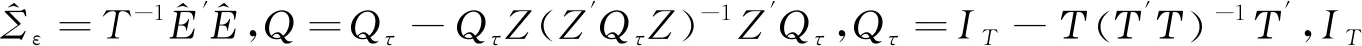
同时,借鉴Toda和Yamamoto(1995)[4]的研究,可以证明(10)式的检验统计量收敛于卡方分布,即
(11)
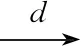
2 实证结果与分析
2.1 数据说明
黄金是国际上影响很大的商品,它不仅具有商品属性,更重要的是具有金融属性.黄金的价格受到产量、销量、美元、原油等因素的影响.本文主要通过影响黄金的一些因素来分析黄金的价格变动.为了保证数据的真实性,采用美国期货交易委员会(CFTC)[6]中的黄金数据,包含商业净头寸、非商业净头寸(净头寸=多头-空头),以及MT4中的黄金价格、美元指数价格和原油价格数据.
根据数据的可获得性,本文实证分析的样本区间为2010年8月至2018年2月,在样本中以当时黄金的价格作为因变量,以黄金的商业净头寸、非商业净头寸和历史黄金价格、美元指数价格、原油价格数据作为解释变量.同时对黄金价格采用对数变换的形式,其他影响因素作标准化变换.
2.2 单位根检验
为检验时间序列正确的形式,首先采用单位根检验判断时间序列是否满足同阶单整.单位根检验问题[7]是检验时间序列的平稳性.本文使用单位根检验中的ADF检验对各变量进行平稳性检验,原假设为“存在单位根”,即数据非平稳.结果见表1.
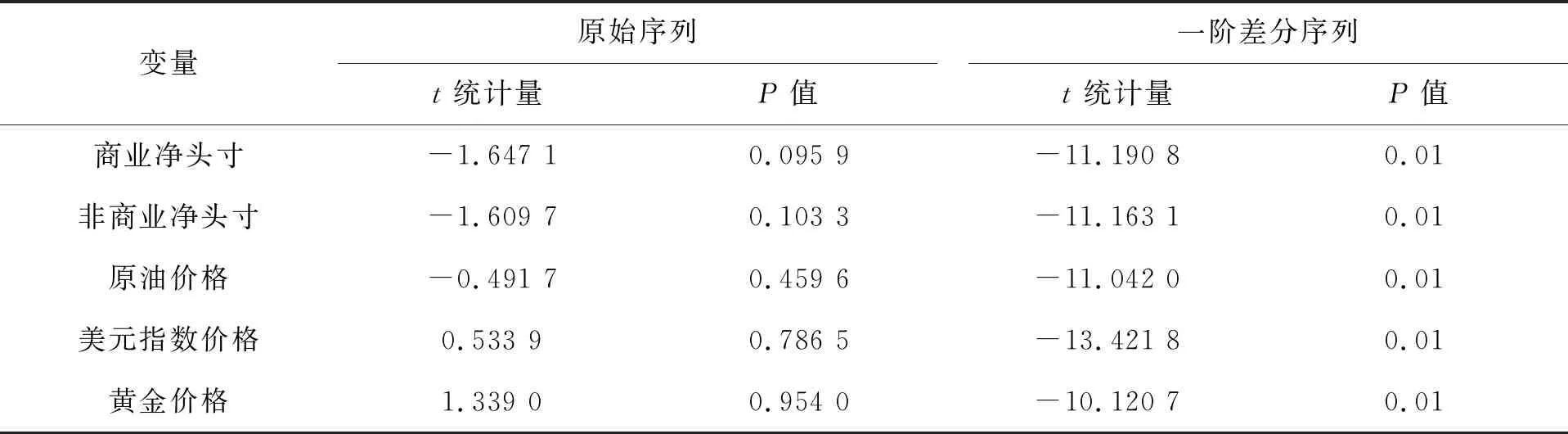
表1 单位根检验
取置信水平为0.05.从表1可以得出,对于原始序列来说,检验结果都是不能拒绝“存在单位根”,即原始数据是非平稳的.为进一步研究,我们对数据进行一阶差分后检验,结果显著地拒绝“存在单位根”,则一阶差分后的5组数据是平稳的,故数据存在一阶单整.
2.3 非线性检验
对黄金价格与商业净头寸、非商业净头寸、美元指数价格、原油价格进行Granger因果检验前,首先需要进行非线性检验,查看它们非线性的动态依存关系.因为传统的Granger因果检验仅对线性依存有明显效果.为保证结论的稳健性,本文采用BDS检验[8]来检验黄金价格与其相关影响因素之间的关系.因BDS检验是在独立同分布的条件下进行的.首先使用VAR模型对5组数据进行线性过滤,以过滤它们之间的线性依存关系,再对其过滤后的残差序列进行BDS检验,结果见表2.
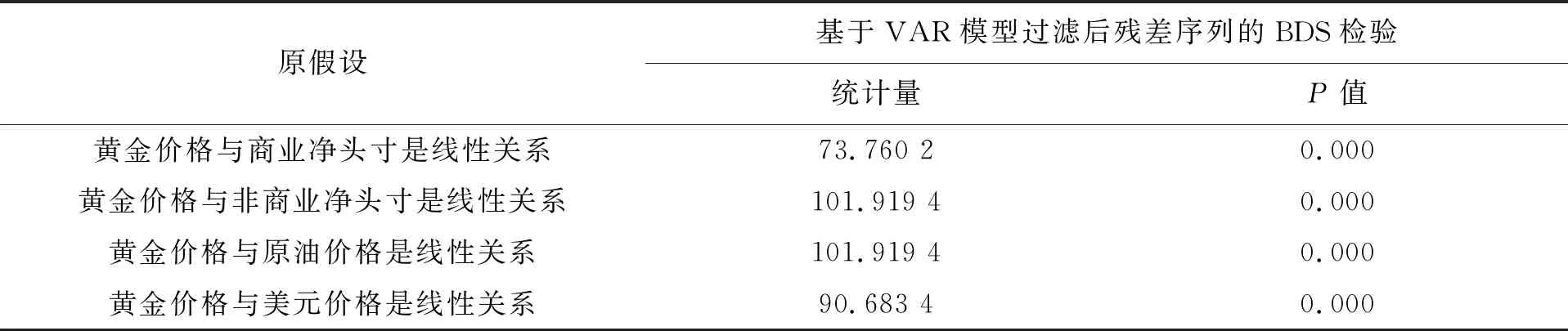
表2 BDS检验
由表2可知,在0.05的显著性水平下,4组检验关系均拒绝线性的原假设,因此可以得到,黄金价格与商业净头寸、非商业净头寸、美元指数价格、原油价格存在显著的非线性动态关系.
2.4 非线性Granger因果检验
由于经典的Granger因果检验无法检验非线性的因果关系,所以为检验商业净头寸、非商业净头寸、美元指数价格、原油价格与黄金价格之间的因果关系,本文使用Wald检验统计量来检验它们之间的非线性因果关系.因数据的简便性,本文选择检验滞后三阶数据的因果关系.检验结果见表3.
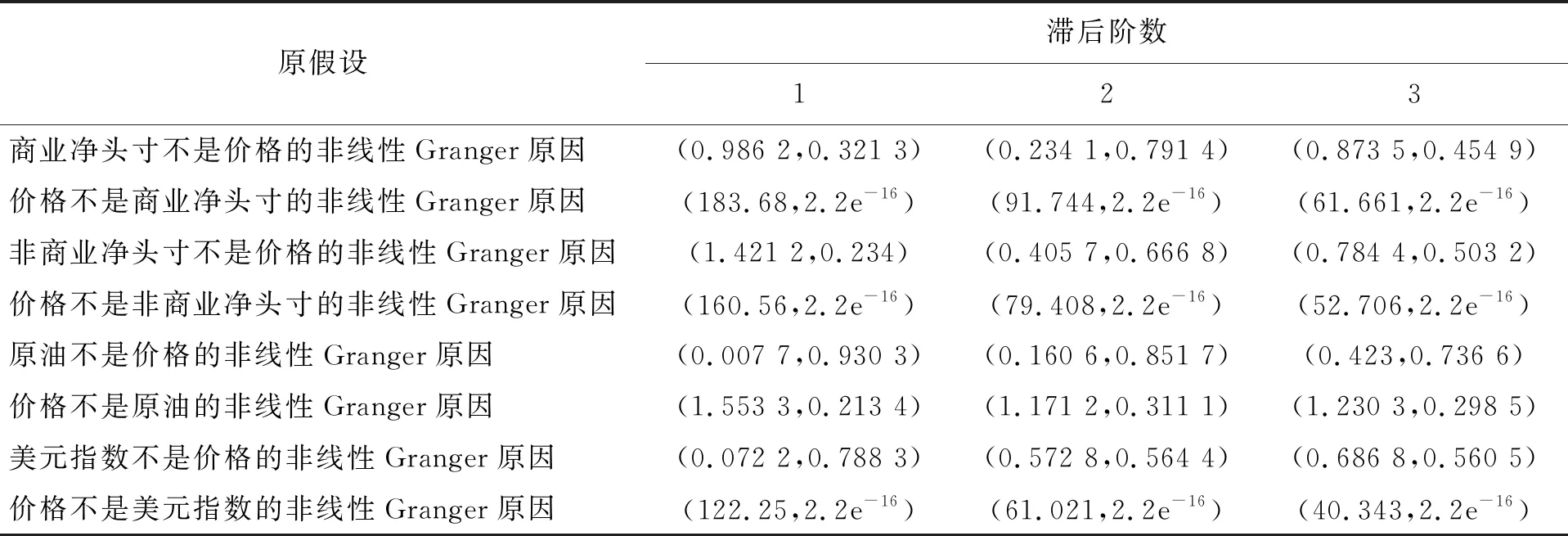
表3 非线性Granger因果检验
注:表3括号中前半部分为Wald检验统计量,后半部分为P值,置信水平α取0.05.
根据检验结果得到,原假设“黄金价格不是商业净头寸的非线性Granger原因”滞后三阶全部被显著地拒绝,即黄金价格是商业净头寸的非线性Granger原因;原假设“黄金价格不是非商业净头寸的非线性Granger原因”滞后三阶全部被显著地拒绝,即黄金价格是非商业净头寸的非线性Granger原因;原假设“黄金价格不是美元指数的非线性Granger原因”滞后三阶全部被显著地拒绝,即黄金价格是美元指数价格的非线性Granger原因;其他假设情况均不拒绝原假设.这与我们实验所得的结果有所偏差.
本文研究时间序列的长期趋势性成分,但一般的非平稳时间序列都包含短期的波动成分,为将长期趋势成分分解出来,这里使用H-P滤波法对数据进行分解[9],剔除时间序列中的波动性成分,再对滤波后的数据进行非线性Granger因果检验.检验结果见表4.

表4 H-P滤波过滤后的非线性Granger因果检验
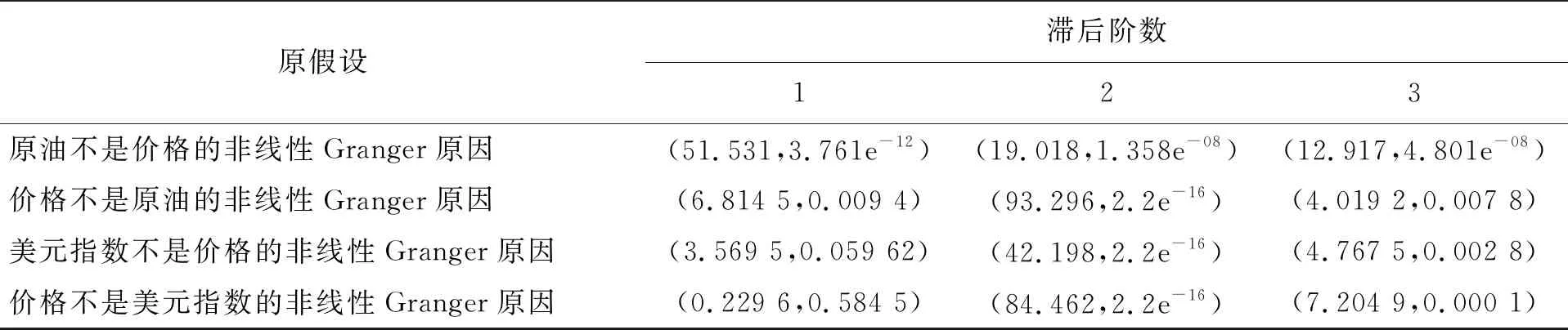
表4(续)
根据表4可以得出,滞后一阶时,除了美元指数价格与黄金价格不互为非线性Granger因果关系外,黄金价格与其他3个因素互为非线性Granger因果关系;滞后二阶时,黄金价格与4个因素互为非线性Granger因果关系;滞后三阶时,非商业净头寸是黄金价格非线性Granger原因,但黄金价格不是非商业净头寸的非线性Granger原因,因此黄金价格与其他3个因素互为非线性Granger因果关系.说明在实际操作中,不能只考虑黄金价格的历史变化这一因素,应该结合原油价格、美元指数价格变化等因素综合考虑黄金价格的未来变化,减少预测误差.虽然Granger因果检验不是数学意义上的因果关系,但在统计学中仍具有研究意义,表明可以用商业净头寸、非商业净头寸、原油价格、美元指数价格的数据来估计黄金价格.
2.5 预测模型的建立及结果分析
本文研究黄金当时价格与历史价格、商业净头寸、非商业净头寸、原油价格、美元指数价格的关系,通过单位根检验可以发现数据一阶差分后平稳.非线性Granger因果检验结果表明,商业净头寸、非商业净头寸、原油价格、美元指数价格是黄金价格的Granger原因.根据以上信息,设黄金价格为Yt、商业净头寸为X1,t、非商业净头寸为X2,t、原油价格为X3,t、美元指数价格为X4,t,建立VAR模型.首先根据模型的简便性,在10以内选择最优的滞后阶数,结果见表5.
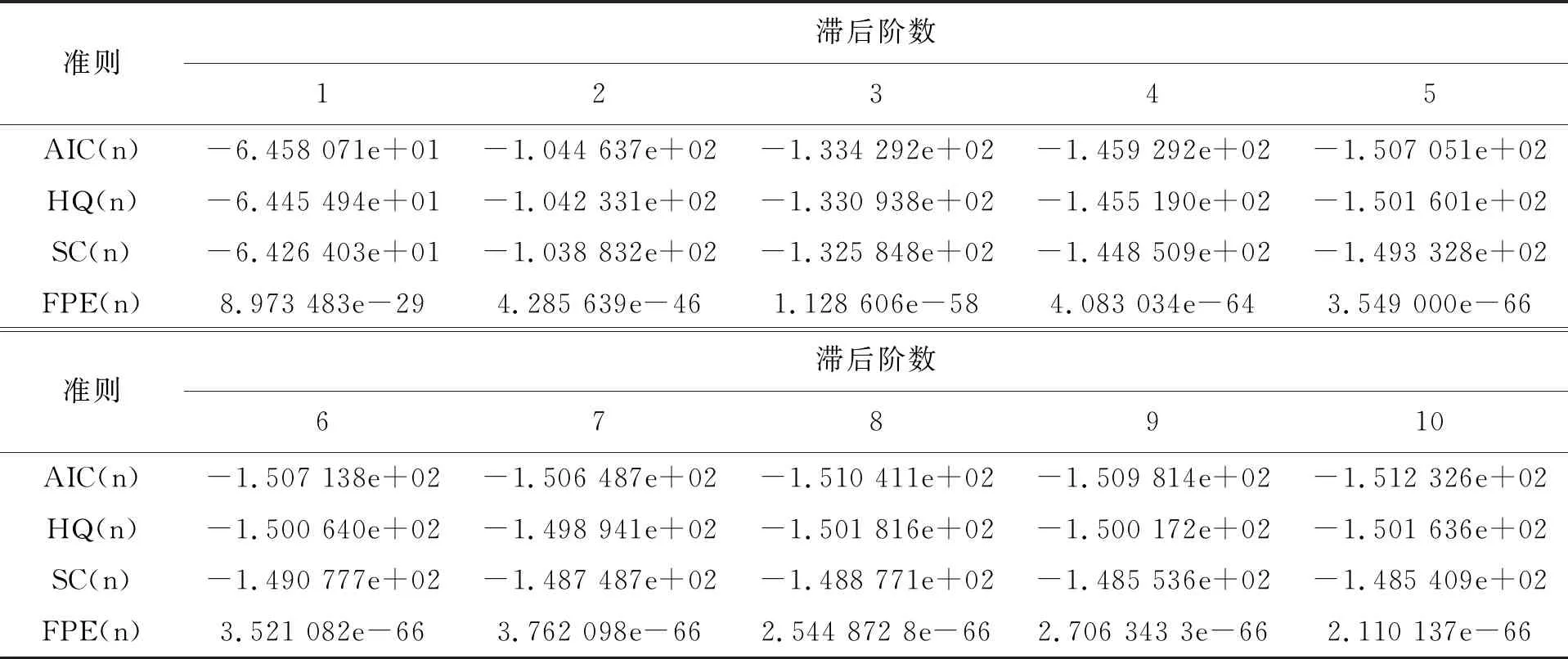
表5 滞后阶数估计
根据AIC准则[10]和SC准则[10],当AIC和SC最小时,模型是最优的,故选择阶数为1建立模型:
Yt=-0.185 127 9+1.025 666 3Yt-1+0.018 689 6X1,t-1+0.019 004 9X2,t-1-0.011 607 0X3,t-1-0.010 965 0X4,t-1.
以上建立的模型Yt为黄金价格、商业净头寸、非商业净头寸、原油价格、美元指数价格滞后一阶对当时黄金价格的预测模型.对上述建立的向量自回归(VAR)模型进行JJ协整检验[11],检验黄金价格、商业净头寸、非商业净头寸、原油价格、美元指数价格是否具有协整关系,若具有协整关系则建立自回归误差修正(VECM)模型,将差分过程损失的信息补充上,以减少回归过程的误差.JJ协整检验结果见表6.
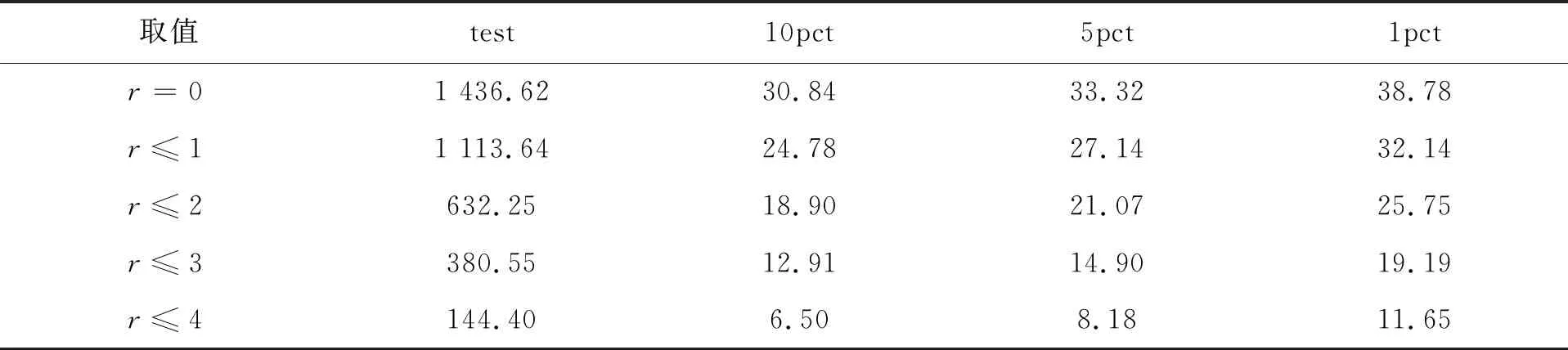
表6 JJ协整检验
从统计检验值可以看出,当r为4时接受原假设,即认为协整向量的秩为4.再根据JJ检验建立修正的向量自回归(VECM)模型:
ΔYt=0.006 199+0.991 6Yt-1-0.023 74X1,t-1-0.022 75X2,t-1-0.000 185 5X3,t-1-0.004 217X4,t-1-0.000 855 9Yt-2-0.000 531 2X1,t-2-0.000 604 3X2,t-2+0.000 039 35X3,t-2+0.000 025 374 46X4,t-2.
由于VECM模型太复杂,为方便计算转化为水平的VAR模型,与VECM模型预测结果相同.
Yt=0.006 198 544+1.991 574 1Yt-1-0.023 736 82X1,t-1-0.022 745 88X2,t-1-0.000 185 483 2X3,t-1-0.004 217 049X4,t-1-0.992 43Yt-2+0.023 205 57X1,t-2+0.022 141 6X2,t-2+0.000 224 832 3X3,t-2+0.004 242 49X4,t-2.
根据建立的VECM模型可以看出,我们建立了黄金价格、商业净头寸、非商业净头寸、原油价格、美元指数价格的预测模型.但本文主要对黄金价格进行研究,即Yt的变化.下面分析其他4个因素对Yt的脉冲响应分析.取95%的置信水平,观察商业净头寸、非商业净头寸、原油价格、美元指数价格的随机扰动冲击对黄金价格当前值和未来取值变化的影响.结果见图1.
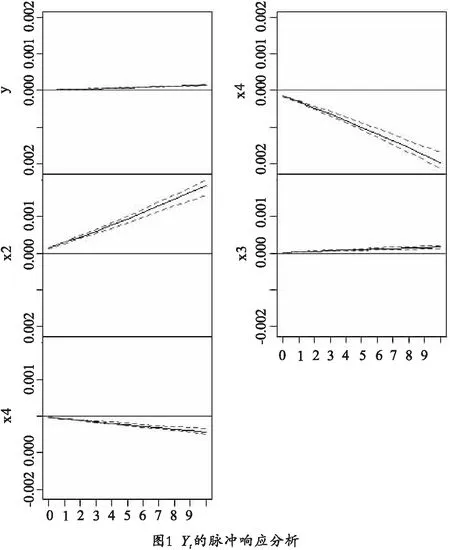
Fig.1 Yt impulse response analysis
通过脉冲响应分析可以看出,黄金的商业净头寸和非商业净头寸随黄金价格变化较大,原油价格和美元指数价格与黄金价格变化较为一致,说明本文选取的4个因素对黄金影响很大.进一步分析预测黄金价格10期的结果,每次代表一周价格,预测到未来两个月的变化,再与真实值进行比较.结果见表7.
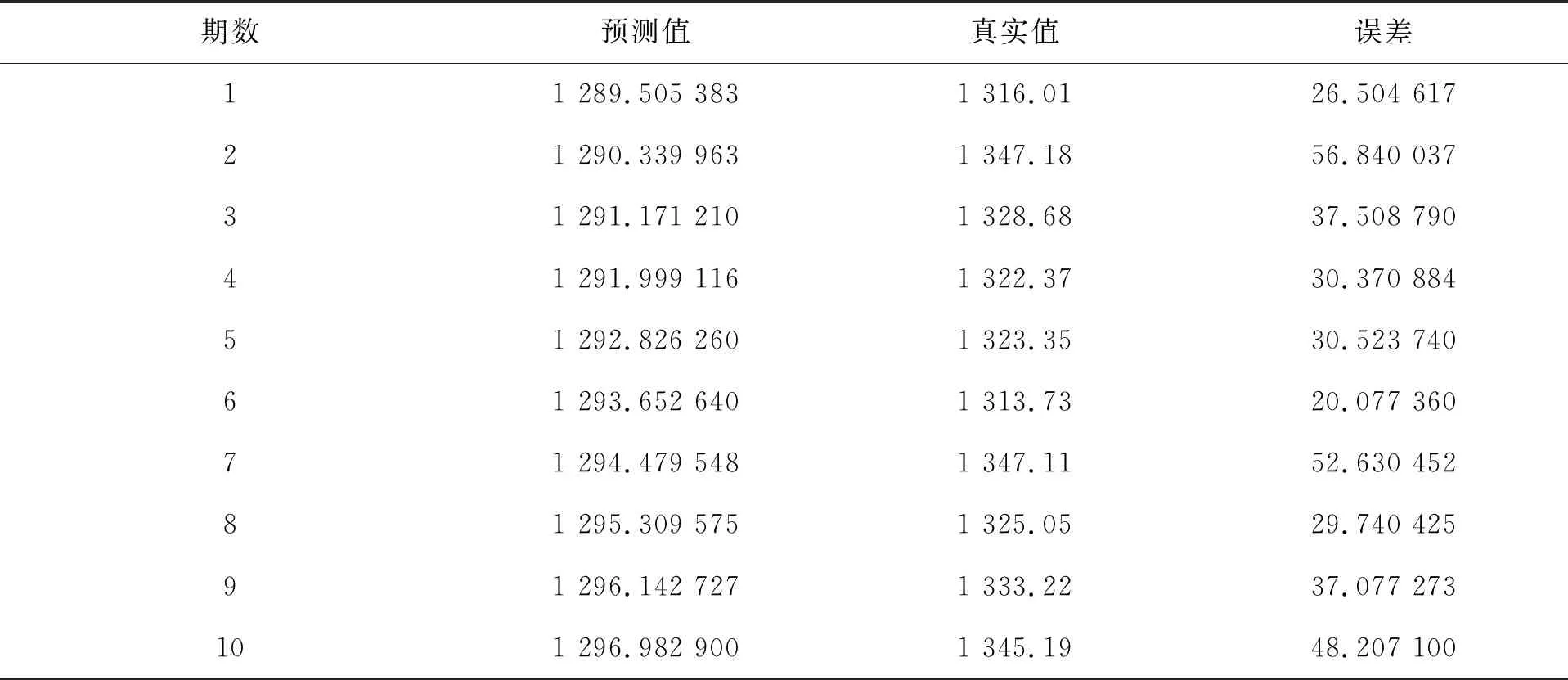
表7 黄金价格估计
通过预测值和真实值之差得到误差,可以观察到我们得到的结果与实际有一定偏离.造成这种结果的原因主要是实际影响黄金价格的因素较多,而本文只考虑4个因素进行量化分析,故对黄金价格的预测结果有一定偏差.但本文基于非线性Granger因果检验对黄金的定量分析以及得出的分析结果,对实际操作仍有一定指导意义.
3 结 论
黄金市场瞬息万变,为更好地研究黄金价格变化,本文采用非线性Granger因果检验对黄金价格进行量化分析.通过实证检验得到,商业净头寸、非商业净头寸、原油价格和美元指数价格与黄金价格呈非线性关系,即存在非线性Granger因果关系,这为我们进一步对黄金的预测提供了有利条件[12].
由于条件的复杂性,本文仅对与黄金价格有关的4个因素进行量化分析.而实际影响黄金价格的因素非常多,故得到的结果与黄金实际价格有所偏差.但基于非线性Granger因果检验为我们后续对黄金的研究起很大作用,也为相关文献作了有益补充.
