Complex Interpolations for Bergman Spaces and Their Applications
2020-04-23GUOYunyunSHENFangningLYUXiaofen
GUO Yunyun, SHEN Fangning, LYU Xiaofen
(School of Science, Huzhou University, Huzhou 313000, China)
Abstract:In this paper, we discuss the complex interpolations for Bergman space with exponential weights using the knowledge of Complex Functions and Functional Analysis. As an application, the boundedness of Berezin transforms on Lebesgue space Lp is obtained.
Keywords:Bergman space with exponential weight; complex interpolation; Berezin transform
0 Introduction
LetDbe the unit disk on complex planeCand let dAbe the normalized area measure onD. For a subharmonic functionφonD, 0 and whereH(D) is the set of all holomorphic functions onD. |ρ(z)-ρ(w)|≤ε|z-w|, wheneverz,w∈DE. We let where Δφis Laplace operator acting onφ. Throughout this paper, we always suppose thatφis a subharmonic function onDwithφ∈W0. This weight is closed to that discussed by Borichev, Dhuez and Kellay in [1] and by Oleinik and Perel’man in [2]. whenever 1≤p≤, which can be seen in [3]. Supposegis a function onDsuch that We then define Berezin transform ofgto be It is easy to check that Berezin transforms can be well defined on the spaceLp. In this paper, we study the complex interpolation for Bergman spaces by the boundedness of Bergman projections. As an application, we also consider the action of the Berezin transform onLpspaces. In what follows, the symbolcstands for a positive constant, which may change from line to line, but does not depend on the functions being considered. Two quantitiesAandBare called equivalent, denoted byA≃B, if there exists somecsuch thatc-1A≤B≤cA. Definition1SupposeX1andX2are Banach spaces. A spaceXin Banach space will be called an intermediate space betweenX1andX2ifX1∩X2⊂X⊂X1+X2with continuous inclusion. The spaceXis also called an interpolation space betweenX1andX2, denote as [X1,X2]=X. Proposition1[5]Suppose 1≤p0≤p1≤and 0≤θ≤1. Then we have where Theorem1Suppose 1≤p0≤p1≤∞ and 0≤θ≤1. Then where which follows from the definition of complex interpolation. there then exist a functionF(z,ζ)(z∈D, 0≤Reζ≤1) and a positive constantMsuch that (a)F(z,θ)=f(z) for allz∈D. (b)‖F(·,ζ)‖p0,φ≤Mfor all Reζ=0. (c)‖F(·,ζ)‖p1,φ≤Mfor all Reζ=1. Define a functionG(z,ζ) to be We get G(z,θ)=Pf(z)=f(z). If Reζ=0, we have Berezin transform plays an important role in Bergman spaces, such as Carleson measures, Toeplitz operators, Hankel operators. In this section, we discuss the boundedness of Berezin transforms acting onLpspaces. We need the following lemmas which can be seen in [3] and [6]. The distancedρ(z,w) is defined as where the infimum is taken over all piecewiseC1curvesγ:[0,1]→Dwithγ(0)=zandγ(1)=w. (1) There exist positive constantsσ,csuch that (2) There exist some constantsα>0,c>0 such that In particularly, K(z,z)≃e2φ(z)ρ(z)-2,z∈D. Lemma2[3]Supposeρ∈0,k>-2,σ>0,- Theorem2For 1≤p≤, Berezin transforms are bounded onLp. ProofUsing the interpolation, we only need to show that Berezin transforms are bounded onL1andL, respectively. In fact, by Fubini’s theorem, we have By Lemma 1 and Lemma 2, we obtain Similarly, The proof is completed. The idea of complex interpolations appears everywhere in mathematics, especially in PDE, harmonic analysis, appriximation theory and operator theory. The method is most successful in dealing with operators which either act on a scale of Banach spaces or belongs to a scale of Banach spaces.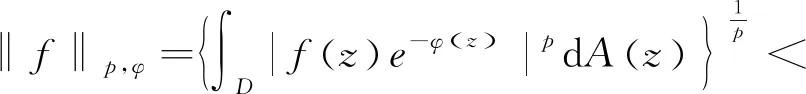



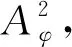
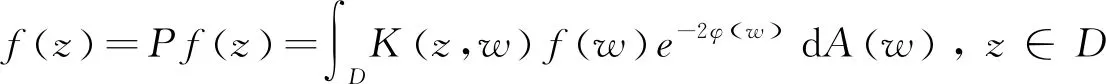

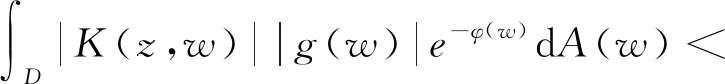
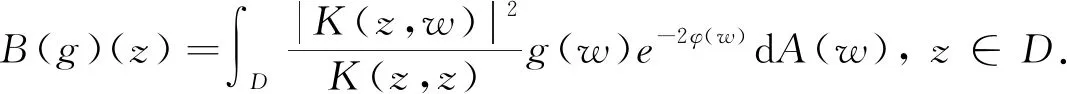
1 Complex interpolation
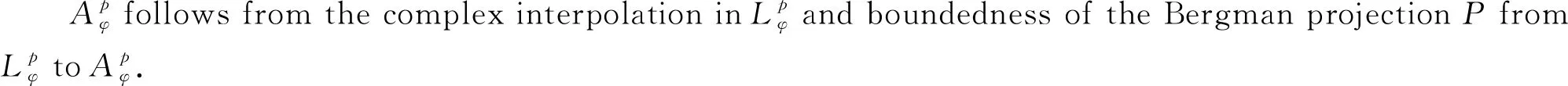
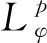
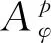
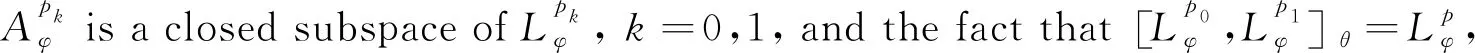
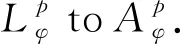
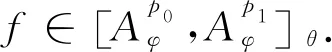
2 Berezin transforms
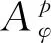


3 Conclusion
