Pasternak地基中盾构施工对平行管线的影响分析

■ 熊晨超，王 彬，魏 纲

(1.义乌工商职业技术学院建筑工程学院，浙江 义乌 322000；2.浙江大学城市学院，浙江 杭州 310015)

随着城市化进程的日益加剧，城市轨道交通进入大发展时期，地下空间开挖过程中，盾构法的应用日益频繁。盾构施工会对邻近土体产生扰动，土体流失会对管线产生较大的附加应力和附加变形，导致管线受损。因此，迫切需要研究盾构开挖对管线的影响规律。在实际的盾构施工过程中，管线平行于隧道分布的情况最为常见。由于地铁隧道、管线在修建过程中很多情况是沿着城市道路走向分布，而相对于管隧正交工况下管线的影响研究，目前关于管隧平行工况下管线的影响研究相对较少。林雄、魏超、周成君、吴为义、李兴高等提出了一种经验或半经验的刚性管线纵向应变计算及安全评价方法，可应用于快速评估管线的潜在损害。盛宏玉、张恒等提出一种经过改进的Pasternak地基模型，发现地基刚度的增大剪应力影响不可忽略。以上研究大多没有进行相应的总结归纳，因此深入研究平行于双线盾构隧道的地下管线性状变形规律具有重要意义。

本文基于盾构法隧道统一土体移动模型三维解，建立双线盾构施工过程中土体损失引起土体沉降的计算方法，基于Pasternak模型，推导出管隧平行施工引起的管线应力、弯矩、变形和应变的计算公式；通过算例验证，表明本文方法的合理性，并探讨了单双线盾构下水平间距、管线埋深以及土体损失率改变对管线竖向位移的影响。

一、本文假定及计算模型

（一）假定模型

Pasternak模型是在Winkler地基模型基础上假定纵向上存在一个剪切薄层，将薄层的剪应力转化为基底法向应力的修正模型。

参照张恒等的受力模型假定，隧道开挖对管线的影响如图1所示。本文仅研究管隧平行工况，R为开挖半径，h为轴线埋深，L为两条轴线水平距离，d为外直径，z0为轴线埋深，x为距开挖面水平距离；y为距轴线的横向水平距离；z为距地面竖向距离。

令隧道开挖引起管线轴线位置处土体竖向位移为S，则管线所受力为：

其中，G是剪切模量，按Tanahashi[1]建议G值选取为：

其中，E0为土体变形模量；μ为泊松比；t为隧道变形深度，徐凌提出t=2.5D。k为管线地基反力系数，Vesic提出长梁(l/m＞10，l、m为地基梁的长和宽)的地基反力系数为：

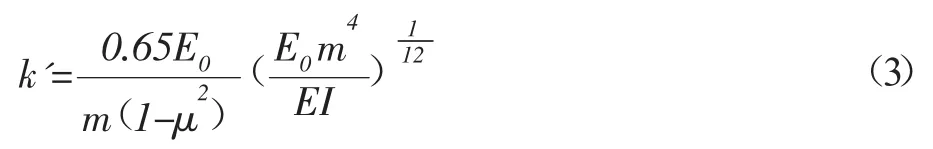
其中，EI为抗弯刚度；m取d。本文采用well[2]建议k=2k'。

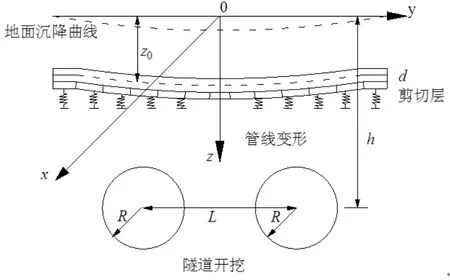
图1 盾构施工对地下管线的影响

（二）平面处的土体沉降S计算

盾构开挖引起土体变形具有三维性，土体损失是土体变形的最大因素，其他因素仅开挖面有影响。

取a=0、μ=0.5时，Loganathan公式表达为魏纲[3]提出的统一土体移动模型二维解的最小解。相比oganathan公式，该解适用所有黏性土工况，采用魏纲建立的土体移动模型三维解，得出下单线盾构施工引起管线平面任一点的土体竖向位移为：

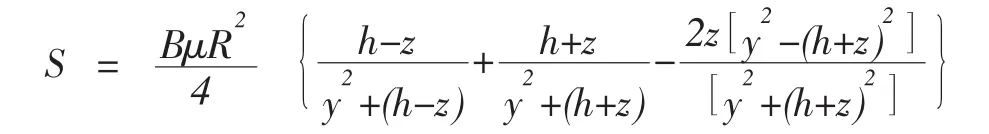
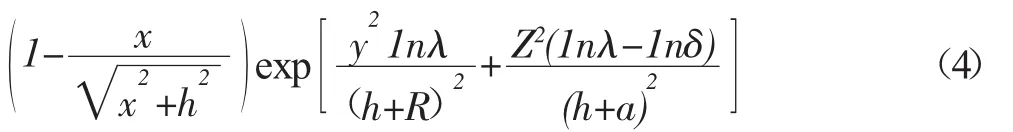
其中，a为土体移动焦点到中心点的距离；η为最大土体损失率；距离掘进方向x处的土体损失率η(x)表达为：

基于文献，魏纲等推导了双线平行隧道施工引起三维土体变形的计算公式，如图2所示。其中，gf、af为先行盾构的土体损失参数和移动焦点至隧道中心点的距离；gl、al为后行盾构的损失参数和移动焦点至隧道中心点的距离。

图2 计算简图

假设右侧先开挖，则双线平行隧道施工引起土体竖向位移为：

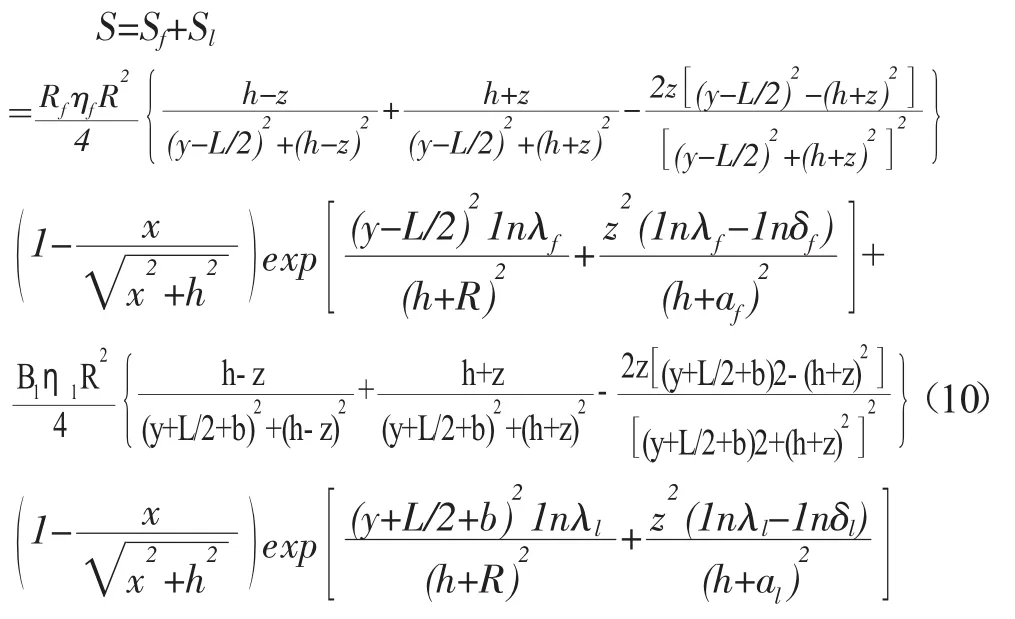
其中，b为后行开挖引起的最大沉降值偏离轴线的距离；ηf、ηl分别为先行和后行盾构产生的土体损失率；Bf、λf、δf为先行盾构计算参数；Bl、λl、δl为后行盾构计算参数。

二、Pasternak模型中管线竖向位移计算

（一）管隧水平时管线受力机理

当隧道轴线位于平行地下管线正下方时，管线变形受盾构施工的影响最大。因此，本文主要分析位于盾构隧道轴线正上方的地下管线受力与变形性状，并主要针对单线和双线盾构下管隧平行距离的影响因素进行分析。采用Pasternak地基模型，考虑盾构施工对土体和管线的影响，提出管线受力和变形的计算模型，其计算示意图如图4所示。

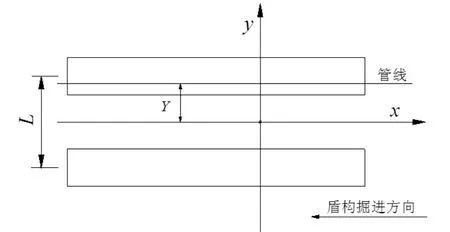
图3 管隧平行计算模型

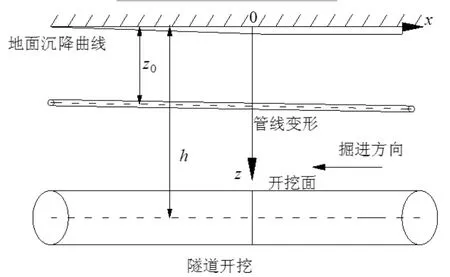
图4 隧道开挖的计算示意图

本文采用魏纲提出的盾构法隧道统一土体移动模型三维解，即式(10)来预测地表纵向沉降，得到管线受隧道开挖影响的变形微分方程为：

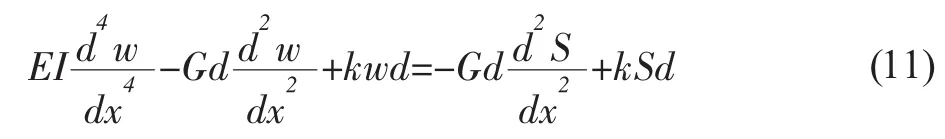
将式(11)整理可得到管线受隧道开挖影响的变形微分方程为：

可得到单线盾构施工中，管线与隧道平行时，地下管线的竖向位移为：

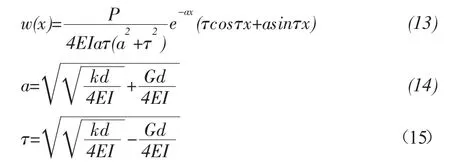
假设隧道开挖时，轴线上任一点ζ上的附加荷载为q(ζ)dζ，根据式(13)，该荷载引起轴线上任意点x的位移dw(x)为：

对式(16)积分，得到由于盾构开挖引起管线竖向位移：

利用公式(17)，分别得到双线隧道施工引起的管线竖向位移计算公式。叠加后得到双线平行盾构施工引起的管线竖向总位移w为：

（二）管线竖向位移计算

（三）管线弯矩及应力应变计算

据公式(13)，无线长梁在Pasternak地基模型上一点集中荷载P，在离荷载作用点x处的弯矩为：

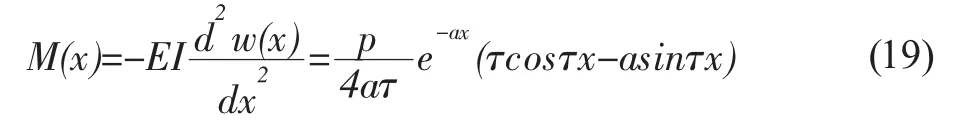
假定隧道轴线正上方对应的点为坐标原点，也为管线的中心点。结合式(1)和式(19)，得到在隧道开挖时，管线在开挖区范围内的任一点ξ的弯矩计算式：

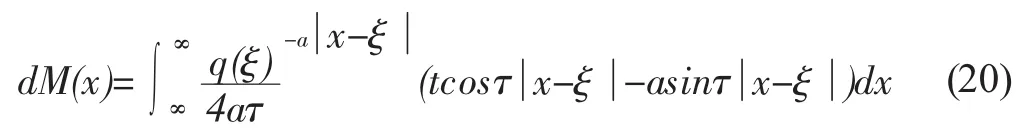
则管线所受的应力计算公式为：

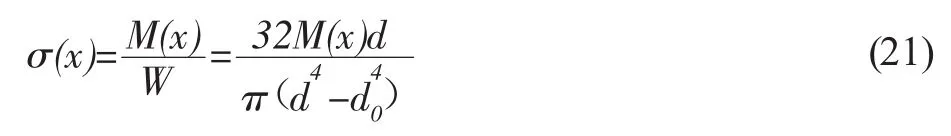
其中，W是惯性矩；d0是管线内直径。

管线应变公式为：

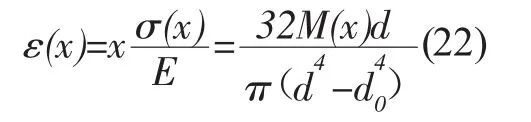
三、算例分析

标准工况说明：工程为双线盾构隧道施工，在双线盾构中轴线正上方处有一管线，与开挖方向平行，管线零位置处即为隧道开挖面，管线为混凝土管，在黏土中开挖。具体参数为：隧道：R=3m，h=15m，L=13.2m；管线：z0=6m，EI=480000kN·m2，d=0.8m；土体：μ=0.3，E0=3.0876MPa。假定 ηf=0.5%，根据魏纲提议 ηl/ηf=0.0283h+0.6933得出ηl=0.56%，假设右侧先开挖，al=0，b=0，af=0.3R，y=0。其它参数与单线开挖一致。

图5为先行盾构和双线盾构施工管线竖向位移对比图。如图所示：(1)地下管线的竖向位移曲线变化规律与累积分布函数较为接近，这与周成君[4]得到的研究结果相同；(2)在x=-15至x=15m范围内管线竖向位移增大较为迅速，在x=20至x=30m内管线竖向位移基本保持不变，斜率趋向为0；(3)先行隧道和双线隧道的管线位移曲线的最大斜率点均位于隧道开挖面x=0处，斜率分别为0.158mm/m和0.313mm/m。

图6为先行隧道和双线隧道施工后管线弯矩比较图。如图所示：先行隧道和双线隧道引起的管线弯矩曲线形状相同，并且变化趋势相同，均以双线隧道中轴线为中心呈反对称分布，有两处正弯矩峰值，两处负弯矩峰值；其中在x=-10处双线隧道引起的管线最大负弯矩=-7.97kN·m，大于单线隧道；在x=10m处管线受到的最大正弯矩=7.95kN·m，大于单线隧道。

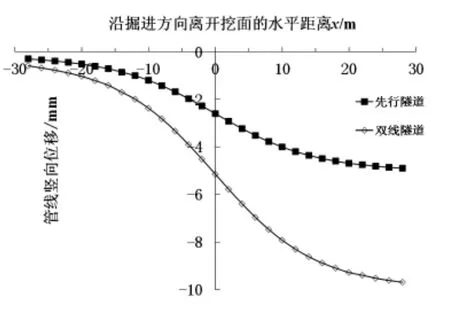
图5 管隧平行时地下管线的竖向位移

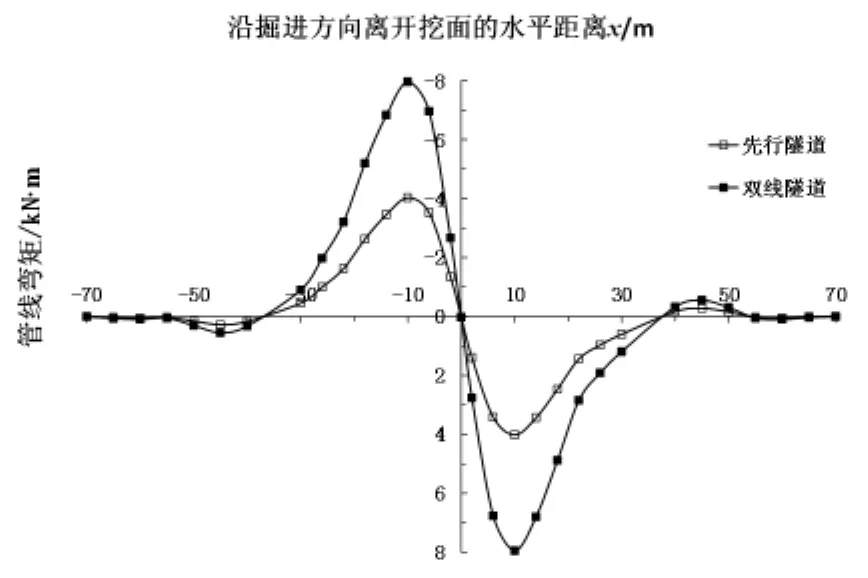
图6 管隧平行时地下管线的弯矩曲线图

四、影响因素分析

（一）单线盾构下管隧水平间距的影响

当地下管线与隧道平行时，管隧水平间距能够直观地表示管线距离隧道的远近，特别是当管隧水平间距为零时，即管线位于隧道线正上方时，受隧道影响比较大。假设坐标原点在单线先行隧道中轴线位置处，取距先行隧道中轴线水平间距分别为y=0m、2m、4m、6m时研究地下管线受盾构隧道施工的影响。

图7为单线盾构施工引起的不同管隧水平间距与管线的竖向位移曲线。可知：(1)管隧水平不同间距时地下管线竖向位移曲线形状相同，接近累积分布函数；(2)管隧水平间距越大，管线的沉降范围和位移量越小，这与陈俊羽[16]、孙宇坤等[17]结论相同；(3)y=0m、2m、4m、6m时管线的最大位移分别为 8.52、8.05、6.84、5.35mm，管线的最大斜率为 0.17、0.22、0.26、0.28mm/m，即管线最大位移、最大斜率都随着水平间距增大而减小。说明管线位于隧道正上方时，管线受施工的影响最大，是最不利的一种空间位置。

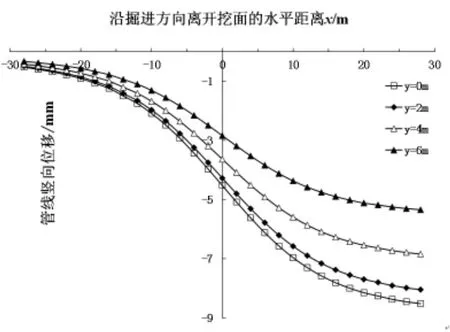
图7 单线隧道施工引起的不同管隧水平间距下管线的竖向位移曲线

（二）双线盾构下管隧水平间距的影响

取距双线隧道中轴线水平间距分别为Y=0m、4m、8m、12m时研究双线盾构隧道施工引起的地下管线受力与变形。图8为双线隧道施工引起的不同管隧水平间距下管线竖向位移曲线，其中Y=0m、4m、8m均处于先行隧道和后行隧道之间。由图可知：(1)不同水平间距下双线施工引起管线竖向位移曲线都接近累积分布函数，处于先行隧道和后行隧道之间的管线竖向位移曲线其主要沉降范围和位移量差距不大，管线的最大斜率和最大位移差距也不大；(2)而Y=12m时管线位于先行盾构轴线右方，管线整体受后行盾构施工影响引起的竖向位移均不大，管线沉降可以看成是先行隧道施工引起的。

图8 双线隧道施工引起的不同管隧水平间距下管线的竖向位移曲线

（三）管线埋深的影响

实际工程中地下管线网错综复杂，但是管线埋深一般在1m～6m之间[2]。因此，本文选取的管线埋深z0分别为1m、2m、3m和4m。图9为管线埋深与最长竖向位移的关系，由图可知：管线埋深的变化对管线竖向位移和管线最大弯矩的影响都不大；z0为1m时，双线隧道引起的管线最大竖向位移为9.32mm，最大弯矩为-7.67kN·m，而在z0为4m时，管线的最大竖向位移为9.84mm，最大弯矩为-8.10kN·m，相较于z0为1m时，位移值增大了5.58%，弯矩值增大了5.6%，影响较小。

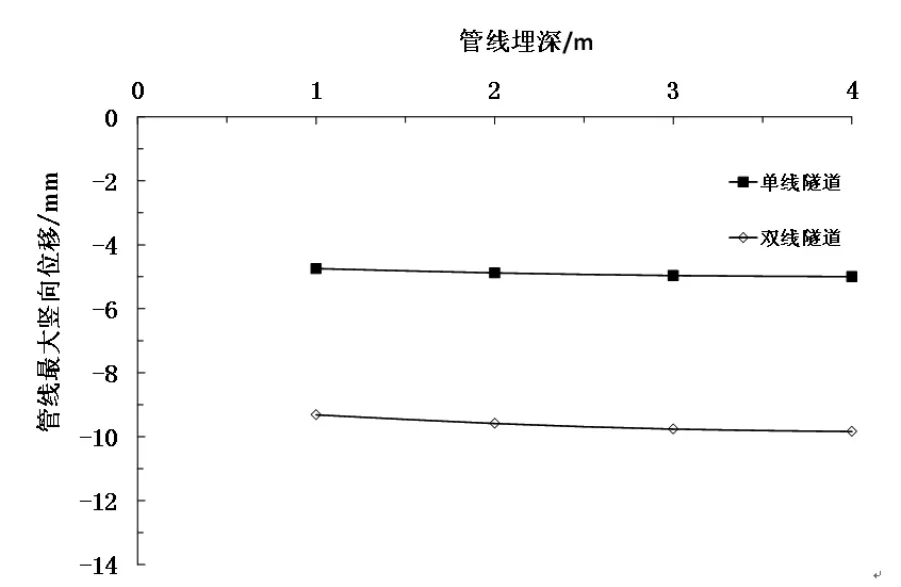
图9 管线埋深与管线最大竖向位移的关系

算例分析表明：单线和双线盾构引起的管线弯矩变化曲线形状相同，并且变化趋势相同，均以双线隧道中轴线为中心呈反对称分布；管线最大弯矩和竖向位移受不同的埋深影响较小，最大弯矩和最大竖向位移都随着土体损失率增大而增大，且较为迅速。不同管隧水平间距下单线和双线隧道施工引起的管线弯矩曲线相同；单线隧道条件下管隧水平间距越大，管线的竖向位移、最大弯矩和最大斜率越小；位于先行隧道和后行隧道之间的不同管线，其竖向位移、最大弯矩和最大斜率均很接近。