扰动诱发高应力岩体开挖卸荷围岩失稳机制

赵光明，许文松，孟祥瑞，刘崇岩

(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001; 2.安徽理工大学 能源与安全学院，安徽 淮南 232001)

高应力岩体的开挖卸荷势必导致围岩产生应力集中，随着围岩应力的增高，其应力状态接近或超过了岩体的极限强度，极易受外界载荷扰动产生失稳。当远场外来载荷与静载叠加合成载荷超过岩体的破坏临界载荷，发生岩爆、冲击地压、瓦斯爆炸等冲击破坏。

岩体工程是一个庞大的地质体，其内部存在大量的节理、结构面、裂隙、构造等，其力学特性在不同加、卸载路径下有明显的区别。哈秋舲[1-2]根据不同岩体工程的不同力学状态，提出了“卸荷非线性岩体力学”的新概念，分析了不同岩石工程中岩石力学的各向异性，归纳为基础工程的主要表现形式为加载，边坡工程的主要表现形式为卸载，而地下工程的主要表现形式为两者共同存在，即切向为加载，径向为卸载。严鹏等[3]将原岩应力场和开挖扰动引起的二次应力进行叠加，分析了圆形隧洞钻爆开挖时开挖边界上初始应力场动态卸荷效应，并计算了其破坏范围。王明洋等[4]研究加卸载条件下岩石的局部破坏特征，岩石在加载和卸载时内部出现的拉应力及其对岩石破坏模式的影响;李邵军等[5]以锦屏II级水电站3号引水隧洞为研究对象，通过事先开挖的平行于引水隧洞的2-1号试验支洞，利用数字钻孔摄像技术，对TBM掘进过程中围岩的开挖损伤区进行原位测试，研究成果为现场支护设计、支护时机、围岩变形特性和地质资料分析提供直接依据;READ[6]、MARTIN[7]、KWON等[8]和YONG等[9]通过数值仿真试验及现场实验得到:开挖卸荷打破了原始应力平衡，导致巷道附近围岩应力场重新分布，当应力大于围岩自身强度时产生破坏，由自由面向岩体内部逐渐扩张。陈景涛和冯夏庭[10]研究表明，卸荷比加载破坏更加剧烈，卸荷条件下岩体主要向卸荷面扩容，发生拉伸张性破坏-劈裂破坏-剪切破坏复合型破坏;李宏等[11]研究表明，高应力岩体开挖卸荷最大切向应力是岩石内部发生张拉性破坏的主要因素;张传庆等[12]研究表明，围压较低时破坏主要表现为拉伸-劈裂破坏，围压较高时破坏主要表现形式转变为剪切破坏;任建喜和葛修润[13]率先开展了岩石卸荷全程CT试验，研究了岩石卸荷过程中损伤裂缝发育破坏的实时演化过程，研究表明，卸荷比加载更加容易破坏，同时具有突发性。李建林和孟庆义[14]根据岩体三轴卸荷试验,研究了卸荷岩体的各向异性特性,如岩体卸荷的应力-应变关系、抗拉强度和变形模量等;李建林等[15]通过制作不同倾角单一预制节理试件，开展节理岩体三轴卸荷试验，研究卸荷条件下节理岩体的应力-应变关系、变形特征、强度特征和破坏模式。目前普遍接受高应力开挖卸荷围岩损伤开裂机制的观点是由于高应力岩体开挖卸荷致使径向卸荷从而引发切向应力集中，造成垂直于最大主应力或平行于开挖方向发生损伤张性拉伸破坏，最终导致岩体整体发生剪切破坏[16]。上述成果对高应力岩体开挖卸荷效应的研究起到了巨大的推进作用，但多数为单轴、双轴卸荷试验，采用真三轴单面卸荷试验更能真实的模拟地下开挖卸荷现象;且在深部地下开挖过程中，开挖临空面不仅仅受卸荷作用，同时轴向爆破引起的动态扰动也是致灾的关键因素。窦林名等[17-19]初步探讨了动静叠加诱发冲击矿压原理并对薄煤层动静叠加诱发机制进行了研究;刘少虹、李凤鸣等[20]试验研究了动静加载下煤的破坏特性及机制。然而针对扰动诱发高应力岩体开挖卸荷损伤围岩失稳机制还需进一步研究。

笔者采用真三轴卸荷扰动岩石测试系统，对高应力岩体开挖单面卸荷渐进性破坏规律进行研究，基于动力扰动波动方程及其扰动能量演化规律，分析不同初始应力、不同扰动振幅、不同扰动频率静动组合条件下高应力岩体单面卸荷力学特征和破坏特征，揭示扰动诱发高应力岩体开挖卸荷围岩失稳机制，对高应力岩体开挖卸荷围岩支护理论起到了重要的作用。

1 扰动诱发高应力岩体开挖卸荷围岩失稳机制

1.1 高应力岩体开挖卸荷效应

岩体在开挖之前处于三维应力平衡状态，开挖导致围岩产生单面卸荷，打破原始平衡，由原始三向六面受力状态转变三向五面受力。由于围岩具有自身的力学特性，一部分地应力以回弹变形的能量发生在开挖临空面，另一部分向深部转移，从而进行应力重新分布产生局部应力集中，当开挖岩体附近围岩应力达到其临界破坏强度时发生局部渐进性破坏，如图1所示，其中，τ为剪切应力;c为黏聚力;σ为法向应力;φ为内摩擦角。临近巷道的围岩经历了应力集中作用过程，从而在巷道周围会形成应力梯度，而应力梯度是导致巷道围岩破坏的重要影响因素之一[21]。不同应力条件下围岩发生梯度破坏宏观和细观特征，随着深度增加，应力梯度更明显[22]。

1.2 扰动诱发围岩失稳机理

地下开挖过程中高应力区域围岩易发生动力破坏，对地下工程施工人员及施工设备构成了相当大的威胁。在离掘进工作面较远的开挖边界附近，围岩常处于欠耦合静动力加载状态，远程触发的动力破坏常发生在高应力岩体开挖过程中。静应力是切向应力集中引起的高应力，动荷载是掘进工作面在平行于掘进轴线圆形围岩中传播的爆破动力波所引起的，如图2所示，其中，σ1为第一主应力;σ2为第二主应力;σ3为第三主应力;σx0为沿x方向地应力;σy0为沿y方向地应力;σz0为沿z方向地应力，在静-动耦合荷载作用下，岩石发生的严重失稳破坏。高应力条件下的围岩破坏可能是由轴向动力扰动载荷触发的具有明显时空滞后特征的动力破坏。

图2 开挖后自由边界附近典型岩石单元的应力状态Fig.2 Stress state of a representative rock element near the free boundary after excavation

1.3 动力扰动波动方程及其传播规律

假设岩体为理想弹性体，根据弹性理论和物理学知识可知扰动三维波动方程为

(1)

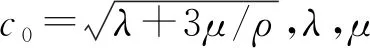
令μ=0，则有

(2)

简谐震动是分析复杂动力扰动的基础，设式(2)解的形式为

p=p(x)ejwt

(3)

式中，w为简谐振动频率;j为x方向;p(x)为一般简谐振动方程。

将式(2)代入式(3)，并整理得

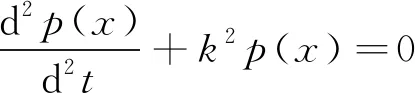
(4)

式中，k为波数，k=w/c0。

常微分方程(4)的解取复数组合形式为

p(t,x)=Aej(wt+kx)+Bej(wt+kx)

(5)

式中，A，B为通解系数。

波动方程

p(t,x)=paej(wt-kx)

(6)

衰减波动方程

p(t,x)=pae-axej(wt-kx)

(7)

反射应力波为

pR(t,x)=γpae-a(2t-x)ej(wt+kx)

(8)

式中，pa为常微分方程(4)特解;pR为反射应力波;γ=(ρ2c2-ρ1c1)/(ρ2c2+ρ1c1)为反射系数，ρ1，c1为一介质密度与波速，ρ2，c2为二介质密度与波速(损伤体可以通过改变介质密度来实现)。

入射应力波与反射应力波叠加得到经过自由面反射后的波动方程:

p(t,x)=pae-axej(wt-kx)+vpae-a(2t-x)ej(wt+kx)

(9)

1.4 扰动能量演化特征

在岩体中取一个微小单元体，其初始体积为V0，外力合力为P，密度为ρ0，速度为v，则该单元体的动能ΔEk为

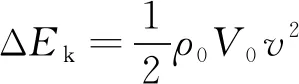
(10)

在扰动作用下，单元体体积将发生膨胀与压缩变形，其形变能ΔEp为

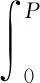
(11)

在平面波传播过程中，只考虑纵波传播时，有

(12)

式中，λ为拉梅弹性常数;Δ为二次函数中代表根的判别式。

由式(12)可得

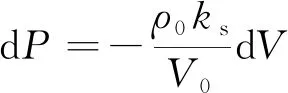
(13)

式中，ks为弹性系数，组合式(11),(13)整理得

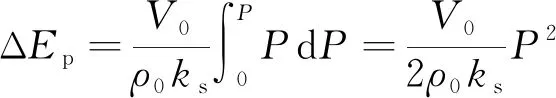
(14)

体积元里总的附加能量(触发能量)为动能与位能之和，即

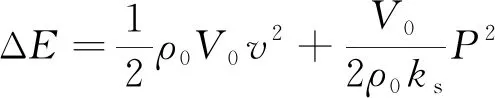
(15)

根据牛顿第二运动定律则有

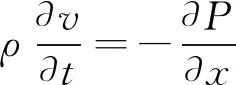
(16)

联立式(7)，(15)，(16)整理得，应力扰动体积元的总能量(触发能量)ΔE为

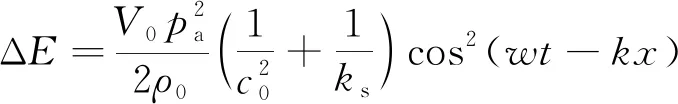
(17)

扰动能流密度Δe为

(18)

2 单面卸荷扰动试验设备及方案

岩石真三轴试验是一种最全面的强度试验，它不仅是建立强度准则的重要资料，更是检验岩石强度准则的最有效依据。岩石真三轴试验可以通过试件3个垂直方向的主应力独立加载、水平方向的一个面突然卸载，来模拟地下工程中开挖后产生临空面导致围岩破坏失稳的现象。

2.1 试验设备

本试验采用自主研发的真三轴卸荷扰动岩石测试系统不仅能够模拟系统三向独立加载高压真三轴状态，获得高应力状态下岩石的力学特性和变形破坏特征，还能够模拟单向或双向突然卸载，监测矿岩的损伤演化和破裂规律，同时可以实现2个方向的扰动(或冲击)，振动扰动载荷范围0～500 kN，频率范围0～50 Hz，可实现点的形式、面的形式进行扰动，如图3，4所示。同时配套声发射监测系统，声发射信号监测选用软岛DS5声发射系统，配合6个声发射探头采集信号，为尽量减少噪音影响，门槛值设定40 dB，声发射采样频率范围设定1 kHz～1 MHz，声发射信号分析软件实时记录AE事件、能量、振幅等参数，并根据采集参数进行三维定位，如图5所示。

2.2 试验方案设计

本文采用自主研发的真三轴卸荷扰动岩石测试系统进行模拟真三轴三向六面受力状态下单面卸荷试验，试件采用完整性和均匀性较好的砂岩，尺寸为100 mm×100 mm×100 mm。

方案1:分级加卸载试验。

为了更好的分析岩样在不同围压单面卸荷的力学特性，1～4号选取砂岩进行分级加卸载试验，分级加卸载试验过程采用液压载荷手动控制对试件进行加载，初始围压见表1。每级应力为10 MPa，加载间隔约15 min[23]，观察声发射信号不发生变化时，证明该处岩石内部应力处于稳定状态，内部损伤破坏不会发展，进行下一步加载。首先，对试件施加初始载荷，模拟地下工程围岩的初始应力状态，然后对最小主应力进行单面瞬时卸荷，第二主应力不变，稳定15 min，再对试件最小主应力卸荷面进行加载至原始应力值，最大主应力在原来的基础上增加10 MPa，然后对最小主应力进行单面瞬时卸荷，如此循环直至破坏，如图6所示。

方案2:单面卸荷扰动试验。

图3 真三轴扰动卸荷岩石测试系统Fig.3 True triaxial disturbance unloading rock test system

图4 真三轴扰动卸荷岩石测试系统加载方式Fig.4 Loading method of true triaxial disturbance unloading rock test system

图5 声发射系统Fig.5 AE systems

假定真三轴卸荷扰动岩石测试系统Z方向为σ1方向、Y方向为σ2方向、X方向为σ3方向。试验过程分为以下3个阶段:① 初始应力加载;② 进行单面卸荷;③ 扰动震源为侧向扰动，波形施加在侧向，应力路径如图7所示，扰动时间函数为

表1 不同初始围压
Table 1 Different initial confining pressures

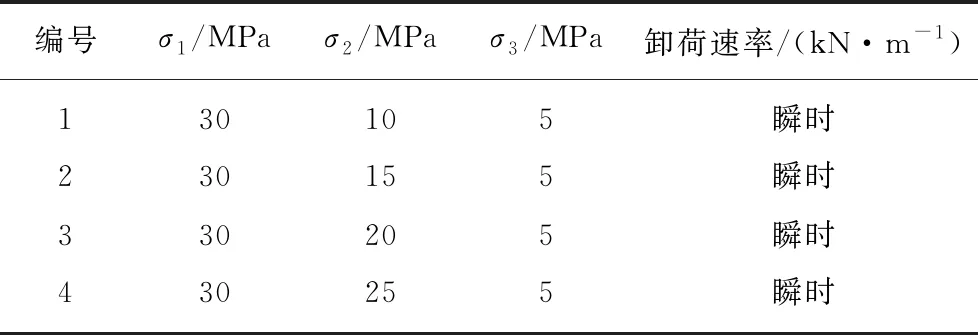
编号σ1/MPaσ2/MPaσ3/MPa卸荷速率/(kN·m-1)130105瞬时230155瞬时330205瞬时430255瞬时

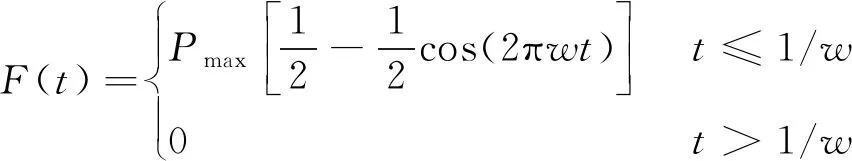
(19)

式中，F(t)为扰动载荷大小，kN;Pmax为扰动载荷的峰值。

图6 分级加卸载试验路径Fig.6 Step loading and unloading test path

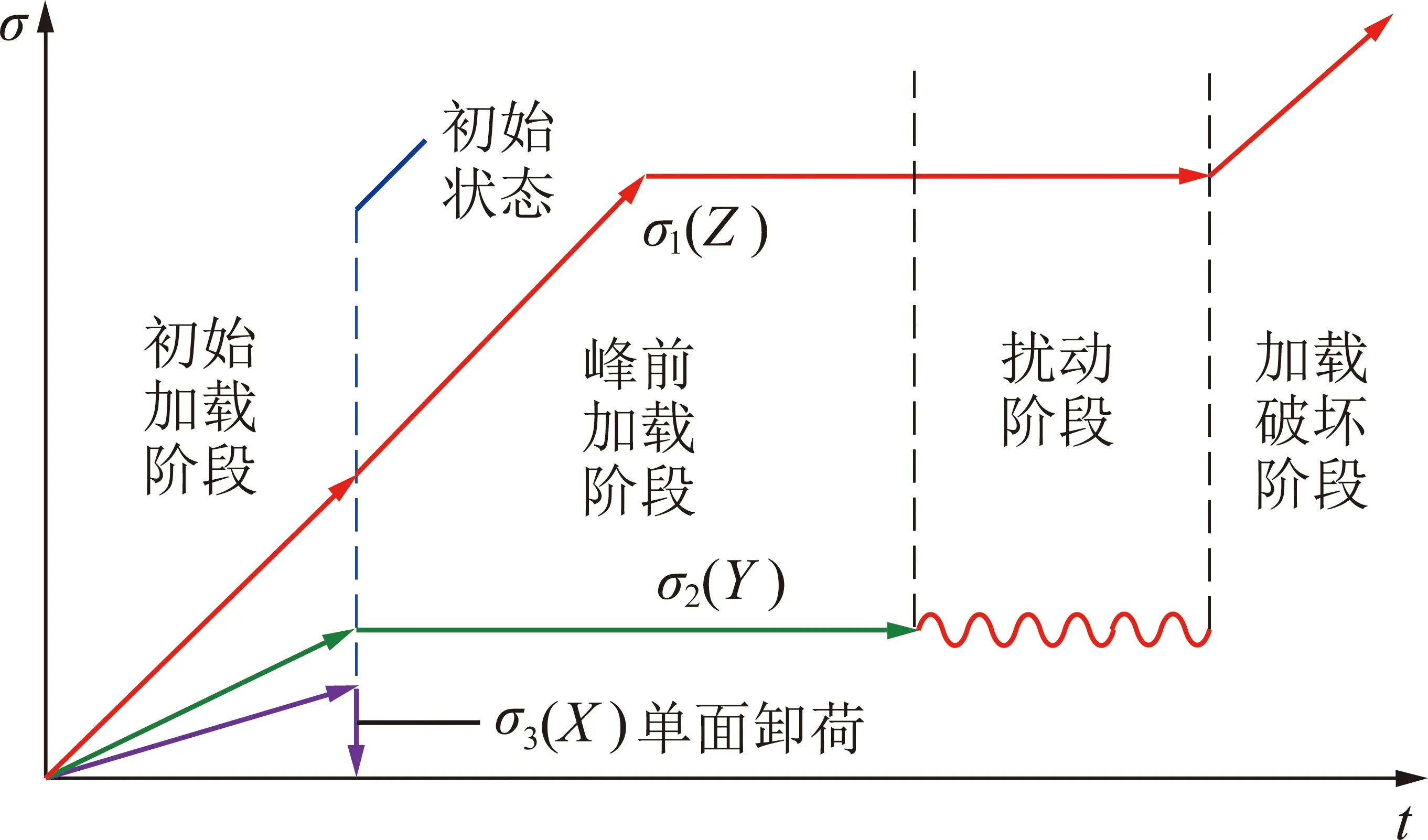
图7 应力路径Fig.7 Stress path

根据文献[17]可知，井下震动最大峰值速度取值范围为0.52～4.38 m/s，频率范围为2～15 Hz，横波速度为2 480 m/s，纵波速度为4 300 m/s，扰动试验选择频率分别为5，10，15 Hz。

根据前人总结的经验公式[22]，可拟合100 kg炸药扰动波峰值随着距离的衰减规律，如图8所示。拟合公式为

y=234.229 99x-2.867 99R=0.999 99

(20)

由式(20)可知，扰动波峰值随着距离的增加而衰减，衰减系数为2.867 99。

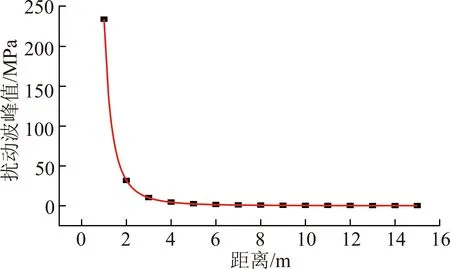
图8 扰动峰值随爆破中心的应力衰减拟合曲线Fig.8 Fitting curve of disturbance peak with the stress attenuation of blasting center

根据文献[24]可知:距掘进工作面3～5 m，应力集中系数最大，最为危险，因此分析主要采用5～10 m的扰动波峰值分别为0.5，1.0，1.5 MPa，具体扰动试验设定值见表2，其中，σt为破坏应力。

3 高应力岩体开挖卸荷围岩渐进性破坏规律

高应力岩体开挖过程出现的变形破坏现象均是岩体开挖应力重新分布导致岩体动力破坏的表现形式，都涉及开挖边界上地应力瞬态卸荷及邻近围岩应力动态调整。同时，伴随岩体开挖必然导致围岩能量的集聚、储存、耗散与释放，上述围岩变形与失稳现象本质上也是能量驱动下的岩体动态破坏。

表2 扰动试验设定值
Table 2 Disturbance test set value

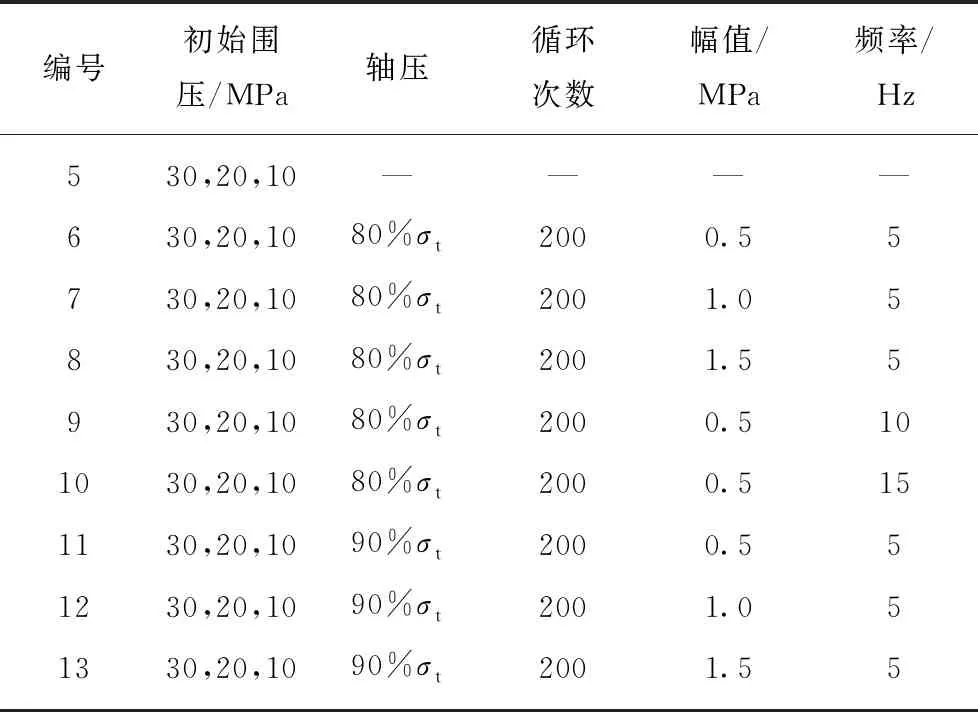
编号初始围压/MPa轴压循环次数幅值/MPa频率/Hz530,20,10————630,20,1080%σt2000.55730,20,1080%σt2001.05830,20,1080%σt2001.55930,20,1080%σt2000.5101030,20,1080%σt2000.5151130,20,1090%σt2000.551230,20,1090%σt2001.051330,20,1090%σt2001.55

3.1 高应力岩体开挖卸荷围岩应力-应变曲线

研究高应力岩体开挖过程中围岩应力与应变能的瞬态调整过程，有助于探明高应力岩体变形破坏的孕育、演化及发生机制，掌握高应力开挖卸荷围岩渐进性破坏规律，为高应力岩体的变形分析及稳定控制提供必要的试验支持。图9为不同围压条件下，试样瞬时卸荷的应力-应变曲线。

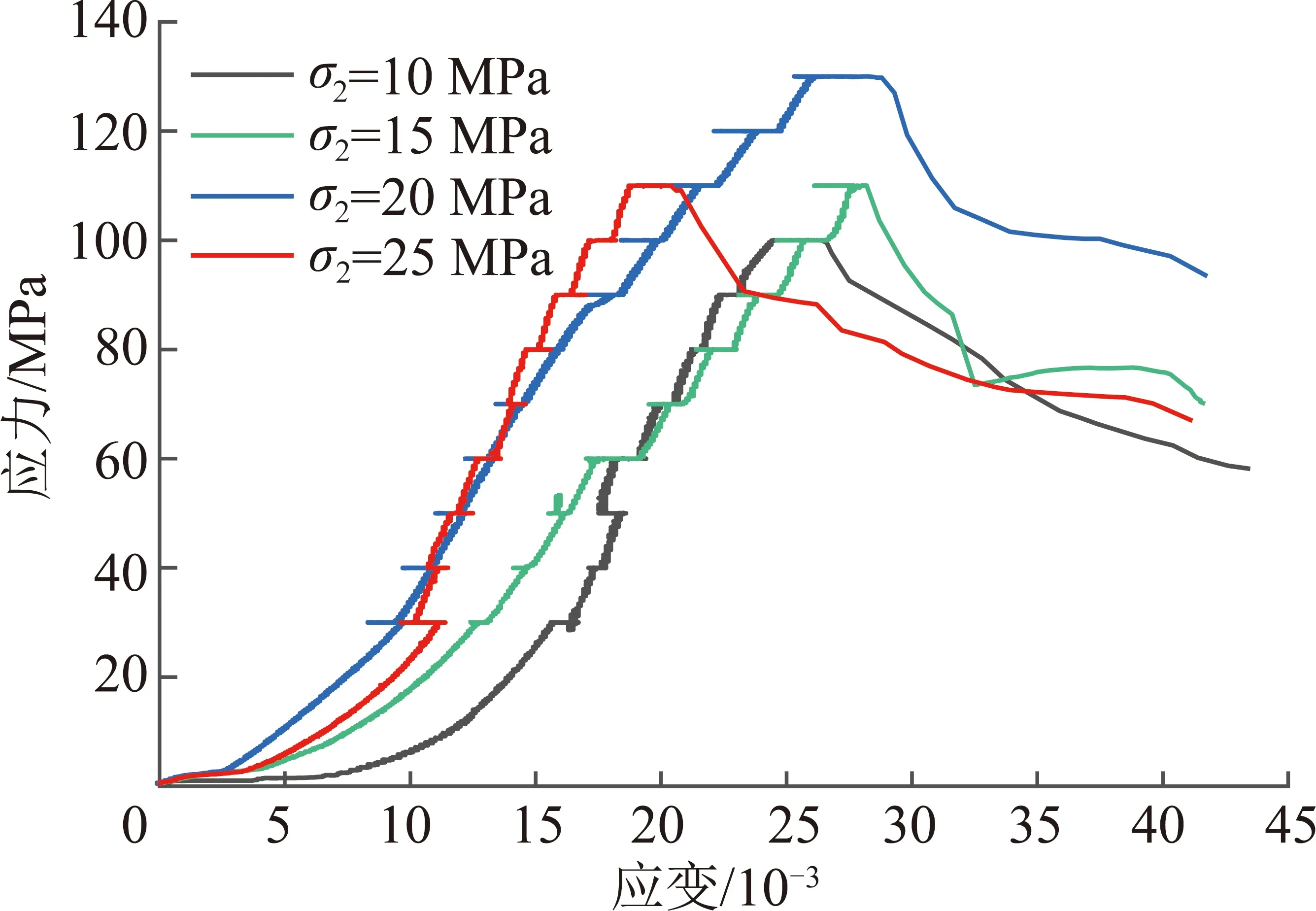
图9 分级加卸载应力-应变曲线Fig.9 Stress-strain curves under graded loading and unloading

由图9可以看出:单面瞬时卸荷时，轴向应变存在瞬时回弹现象，说明岩体由于3向受压，存储大量的能量，在最小主应力单面瞬时卸荷时，有惯性力的存在，岩体发生瞬时扩容;随后轴向应变存在一个增大的过程，到某个值时固定不变，说明岩样单面卸荷后，由于第二主应力的限制，扩容方向主要向临空面扩展，在轴压不变的情况下，应变增大，因此可以看出，单面卸荷后岩体存在一个流变的时间效应。随着第二主应力的增加，破坏时轴向应力发生改变，且单面卸荷后发生破坏的时间也不同，见表3。

表3 不同主应力单面卸荷轴向应力及破坏时间
Table 3 Single side unloading axial stress andfailure time with different principal stresses

第二主应力/MPa轴向应力/MPa破坏时间/min10100101511032012012511013

随着第二主应力的增大，破坏强度呈现一个先升高后降低的一个过程，第二主应力为20 MPa处是破坏强度的转折点。由此可以看出，初始围压越大储存的能量越多，开挖卸荷后释放的能量就越多，沿卸荷面产生的变形就越大、越剧烈。

3.2 高应力岩体开挖卸荷巷道围岩破坏特征

为了进一步分析瞬时卸荷试样的宏观破坏特征，对试样施加不同围压情况下，进行单面瞬时卸荷，从而对比分析其差异。通过图10可以看出:试样卸荷面都产生了劈裂成板的现象，在第二主应力为10 MPa时，试样内部出现剪切裂纹;随着第二主应力的增加，试样内部剪切现象逐渐消失，出现的劈裂裂纹增加，在第二主应力为20 MPa时，试样内部基本全部处于劈裂破坏。说明试样进行单面卸荷，第二主应力限制了其应变扩展方向，对卸荷破坏的最终形态呈现着关键因素。

根据岩石Kaiser效应的特点，将试件应力-应变曲线与相应的声发射振铃计数、能量计数进行分析处理，如图11，12所示。

图10 分级加卸载宏观破坏Fig.10 Macroscopic failure diagram of hierarchical loading and unloading

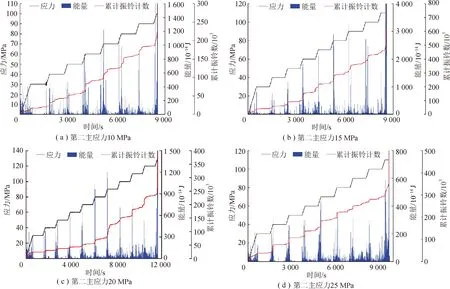
图11 应力和能量-振铃计数-到达时间演化曲线Fig.11 Stress and energy ringing count arrival time evolution curves

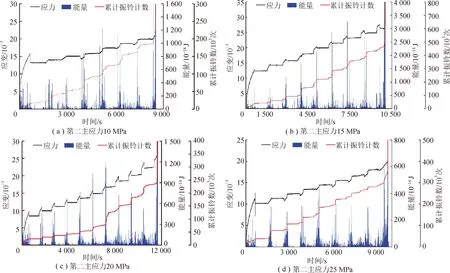
图12 应变和能量-振铃计数-到达时间演化曲线Fig.12 Strain and energy ringing count arrival time evolution curves

图13 单面卸荷Fig.13 Single side unloading

结合图11，12中声发射撞击数、能量及计算参数的时间演化曲线，可以看出，在试样加载至初始围压过程中，产生大量声发射，同时出现一个峰值，能量增大，这是由于试样处于压密阶段，原有微裂隙在载荷作用下闭合发生变形;当达到初始围压后，进行最小主应力瞬时单面卸荷，轴向应力不变，应变瞬间减小，同时能量突然减小，AE事件数急剧增加。在稳定的15 min内，能量几乎没有改变，AE事件数缓慢逐渐增加;当最小主应力单面卸荷15 min后，最小主应力卸荷面加至初始围压，然后轴压在原来基础上增加10 MPa，能量急剧增加，在轴压加载结束后，能量出现一个峰值，AE事件数在此过程中也急剧增大。随着轴压的增大，在轴压加载过程中的能量峰值增大，AE事件数呈现阶梯状增加;说明试件在初始加载过程中，外部对系统做功积聚为应变能，在应力保持过程中声发射不再发生，处于平静期;当进行最小主应力瞬时单面卸荷时，试件内部突然发生应力调整，声发射急剧增加，产生塑性变形;提高轴向压力后应力保持以及单面卸载产生的AE事件数突然上升，伴随能量骤降。当应力达到试验的失稳强度时，试件产生整体破坏，伴随着声发射事件急剧增加。随着第二主应力的增大，岩样破坏强度呈先增加再减小的过程。

4 扰动诱发高应力单面卸荷岩体破坏试验结果分析

在分析扰动诱发高应力岩体开挖破坏之前，首先对单面卸荷破坏的力学特性进行研究，围压σ1=30 MPa,σ2=20 MPa,σ3=10 MPa时的应力-应变曲线、破裂形态及声发射定位，如图13所示。声发射定位图中绿色小球代表初始围压瞬时单面卸荷，岩样内部的损伤破坏;蓝色小球代表扰动情况下，岩样内部的损伤破坏;红色小球代表最终破坏时，岩样内部的损伤破坏情况。

4.1 单面卸荷力学特性及破坏分析

由图13可以看出，岩样在发生破坏时分为3个阶段;第1个阶段，弹性阶段。此阶段岩石应力-应变曲线呈线性变化，内部无裂纹扩展。第2阶段，缓慢变形阶段。此阶段岩石内部产生微裂纹，卸荷面产生的微裂纹较多，当轴压达到126 MPa时，体积应变向卸荷面急剧扩展，轴向应变迅速增大，卸荷面产生板裂破坏，声发射定位与破坏形态基本吻合。第3阶段，变形加速失稳阶段。由于岩体单面卸荷变形本构呈非线性关系，岩体承载能力不能和外载同步线性增长，当轴压达到152 MPa时，岩石发生失稳整体破坏。

4.2 不同扰动幅值力学特性及破坏分析

岩样采用相同的静载与不同扰动振幅组合试验，岩样单面卸荷抗压强度为152 kN，静载取80%，即121 kN，振幅分别为0.5，1.0，1.5 MPa，频率为5 Hz，扰动200个循环，其应力-应变曲线、破裂形态及声发射定位，如图14所示。

由图14可以看出，当静载为破坏强度的80%时，扰动振幅为0.5 MPa，扰动200个循环，破坏强度为148.6 MPa;当扰动振幅为1.0 MPa时，相同条件下的破坏强度为138.6 MPa;当扰动振幅为1.5 MPa时，扰动在160个循环时发生破坏。说明动静组合作用下，静载相同时，随着扰动振幅的增加，动载对岩体的能量输入越大，引起的损伤越大，致使岩体的破坏强度越低。由破坏形态和声发射定位可以看出，当静载一定时，岩样破坏过程动载占主导，扰动振幅较小时，岩样破坏形态和单面卸荷破坏形态一样呈现复合破坏，振幅进一步增高时，岩样表现为劈裂破坏，破坏更为充分，声发射空间分布与其破裂形态基本相吻合。

4.3 不同扰动频率力学特性及破坏分析

岩样采用相同的静载与不同扰动振幅频率组合试验，岩样单面卸荷抗压强度为152 kN，静载取80%，即121 kN，频率分别为5，10，15 Hz，振幅为0.5 MPa，扰动200个循环，其应力-应变曲线、破裂形态及声发射定位，如图14(a),15所示。

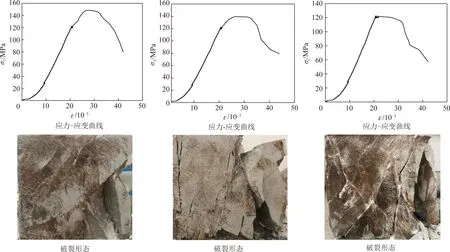
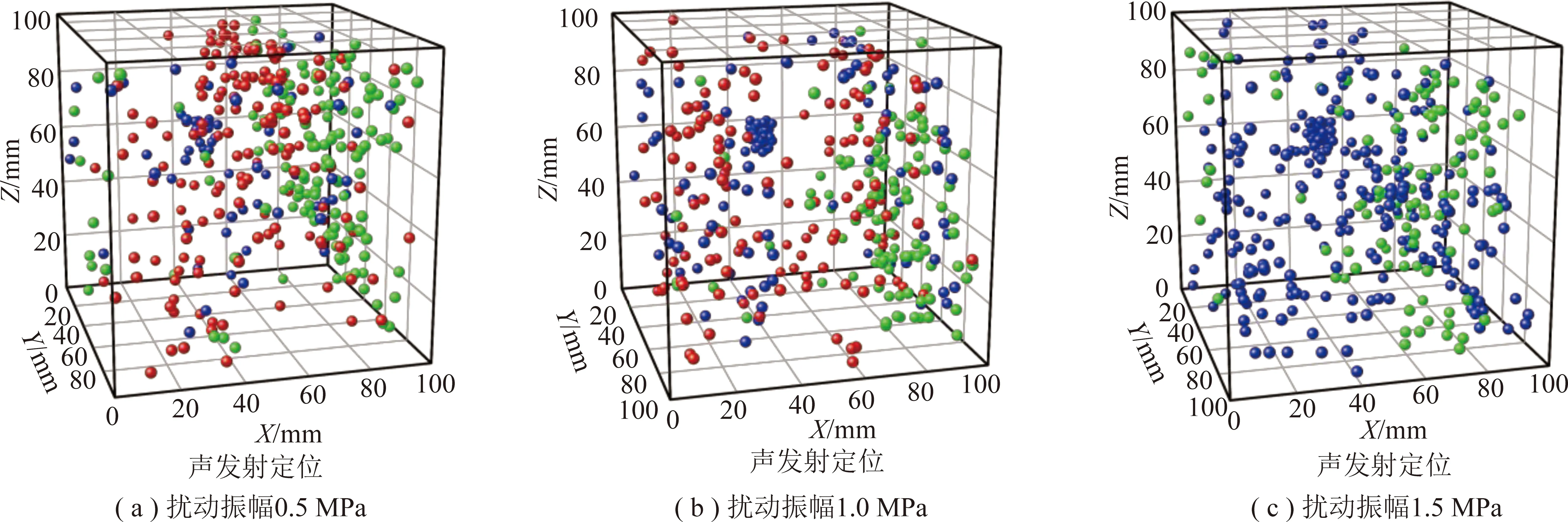
图14 扰动频率5 Hz、静载80%时不同扰动振幅下的应力-应变曲线、破裂形态、声发射定位Fig.14 Stress-strain curves,fracture morphology and acoustic emission location under different disturbance amplitudes at 5 Hz disturbance frequency and 80% static load

图15 扰动振幅0.5 MPa、静载80%时不同扰动频率下的应力-应变曲线、破裂形态、声发射定位Fig.15 Stress-strain curves,fracture morphology and acoustic emission location under different disturbance frequencies with disturbance amplitude of 0.5 MPa and static load of 80%

由图14(a)，15可以看出，当扰动频率为5 Hz时，扰动经历200个循环未发生破坏，随后进一步加载至148.6 MPa岩样发生整体破坏;当扰动频率为10 Hz时，扰动经历200个循环未发生破坏，随后进一步加载至124.8 MPa岩样发生整体破坏;当扰动频率15 Hz时，岩样扰动130个循环时发生整体破坏。由此可见，扰动频率越高，岩样破坏强度越低，这是由于扰动频率越大，岩样扰动应变率越大，对内部损伤也越大。从破坏形态和声发射定位分析，扰动频率越大，循环动载对岩样卸荷面损伤累计越明显，破坏越严重，拉伸-剪切复合破坏转化为劈裂破坏，与声发射空间分布基本吻合。

4.4 不同静载条件下扰动力学特性及破坏分析

岩样采用不同静载扰动组合试验，岩样单面卸荷抗压强度为152 kN，静载取80%,90%，即121，136 kN，频率为5 Hz，振幅为0.5，1.0，1.5 MPa，其应力-应变曲线、破裂形态及声发射定位，如图14(静载取80%)，16(静载取90%)所示。

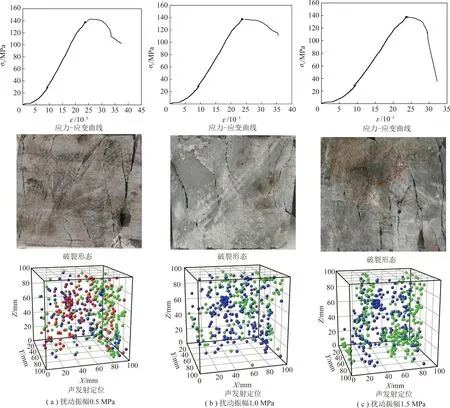
图16 扰动频率5 Hz、静载90%时不同扰动振幅下的应力-应变曲线、破裂形态、声发射定位Fig.16 Stress-strain curves,fracture morphology and acoustic emission location under different disturbance amplitudes at 5 Hz disturbance frequency and 90% static load

由图14，16可以看出，静载是单面卸荷整体破坏强度的90%进行扰动时，振幅为0.5 MPa，扰动200个循环，岩样的整体破坏强度为142.4 MPa;相同条件下振幅为1.0 MPa时，扰动120个循环岩样整体发生破坏;相同条件下振幅为1.5 MPa时，扰动80个循环岩样整体发生破坏。当静载较小时，一定动载反复对岩样进行扰动，虽然产生了一定的损伤，但是未发生破坏;当静载较高时，较小的动载扰动即可诱发岩样的破坏。由此可知，静载的大小与岩样的强度是决定破坏的关键因素，静载越高，岩样整体破坏强度越小，随静载的增大，岩样整体破坏所需动载强度逐渐减小，静载越趋近于岩样整体强度，动静组合加载时，岩样破坏所需扰动能量越小;若静载远远小于岩样的强度，一定强度的动载很难诱发岩样整体破坏。声发射空间分布大致与岩样破坏形态重合，岩样强度越高，声发射时间越多。

5 结 论

(1)采用真三轴卸荷扰动岩石测试系统，对试样三向六面加载不同第二主应力单面卸荷，与现场巷(隧)开挖两帮产生临空面接近，真实的模拟了开挖导致围岩渐进性破坏的现象。

(2)高应力岩体单面瞬时卸荷时，轴向应变存在瞬时回弹-压缩流变现象，轴向应力越大，回弹量越小，压缩量越大其破坏形式为拉伸-劈裂-剪切破坏复合破坏，第二主应力对卸荷破坏的最终形态呈现着关键因素，且随着第二主应力的增大，破坏强度呈现一个先升高后降低的一个过程，第二主应力为20 MPa处是破坏强度的转折点。

(3)动静组合作用下，静载的大小与岩样的强度是决定破坏的主要因素，静载越大岩体破坏所需的触发能量越小，静载相同时，随着扰动振幅、频率的增加，岩体的破坏强度越低，对高应力岩体开挖卸荷围岩支护理论起到了重要的作用。