一道赛题引出的一个有趣结论
2020-04-22杨云奎
杨云奎


我们知道,过中心对称图形对称中心有无数条直线将其面积等分,如圆是一个中心对称图形,过圆心的每一条直线都将其面积等分,对于非中心对称图形,是否也存在过某个点也有无数条直线将其面积等分呢?本文以一道全国初中数学竞赛试题为例进行探究,并给出了肯定的回答。
1 试题及参考解答
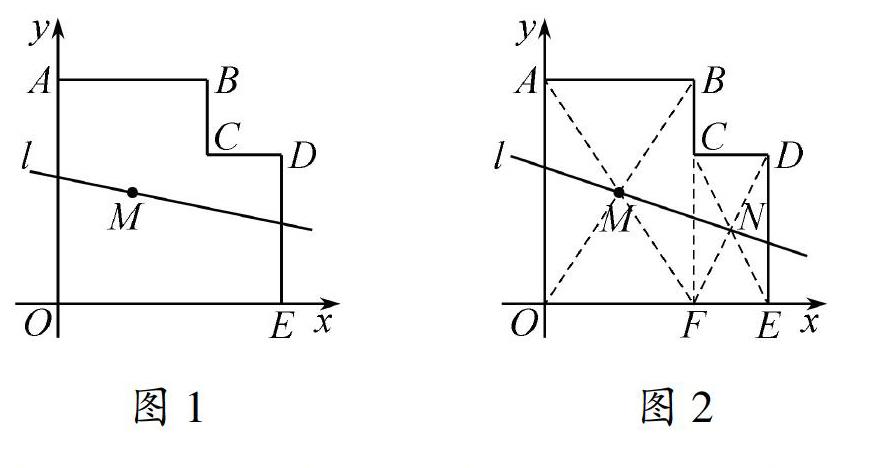
题目(“《数学周报》杯”2010全国初中数学竞赛)如图l,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(O,O),A(O,6),B(4.6),C(4.4),D(6.4),E(6.0),若直线J经过点M(2.3),且将多边形OABCDE分割成面积相等的两部分,则直线J的函数表达式是____,
解如图2.延长BC交x轴于点F:连接OB,AF,连接CE,DF,且相交于点N
由已知得:点M(2.3)是OB,AF的交点,即点M为矩形ABFO的中心。所以直线l把矩形ABFO分成面积相等的两部分,又因为点N(5.2)是矩形CDEF的中心,所以,過点N(5.2)的直线把矩形CDEF分成面积相等的两部分,
于是,直线MN即为所求的直线l,
参考解答是基于对图形的观察,发现了多边形OABCDE的边BC延长后,可以把原多边形分成两个矩形,即矩形CDEF和矩形ABFO,
我们知道,矩形是中心对称图形,过其对称中心的任一直线把它的面积平分,而题中要求的直线J经过的定点M恰是矩形ABFO的对称中心,因此只要写出另一矩形CDEF的对称中心坐标,便能求得直线l的函数表达式,参考解答,确是按照这一思路求出了直线l函数表达式的,
2赛题的一般性解法
解设过点M(2.3)直线l的函数表达式为y=kx+b,所以有3:2k+b,即b=-2k+3.此时直线l可表示为r=kx-2k+3.
5 结论
我们知道,过中心对称图形对称中心的任一条直线都将其面积等分,对于非中心对称图形,通过上述讨论可以得出以下论断:对于某些非中心对称图形,存在两个点,经过每一个点都有无数条直线等分其面积。
