基于ANSYS Workbench软件的软刚臂结构轻量化研究*
2020-04-22董海防王伟伟
□ 李 慧 □ 董海防 □ 朱 刚 □ 李 剑 □ 王伟伟
武汉第二船舶设计研究所 武汉 430064
1 研究背景
单点系泊系统主要用于将油轮、浮式储油卸油装置和超大浮体定位于预定海域,使船舶具有风向标效应,在各种风浪流作用下船舶的受力最小。单点系泊系统实物图如图1所示。软刚臂是单点系泊系统的重要构件之一,通过自重及压载水质量为单点系泊系统提供回复力。为满足各种设计参数、环境载荷、使用要求、作业形式和产品特性,需要对软刚臂结构进行强度分析和结构优化,笔者基于ANSYS Workbench软件对软刚臂结构进行轻量化研究。

2 软刚臂结构
单点系泊系统的软刚臂采用双瓶式基本形式,主要由压载水舱、横杆、轭架和轭架铰接头四部分组成。两个压载水舱通过连接座与系泊腿下部万向节相连,压载水舱之间通过横杆连接。两个压载水舱与轭架采用锥段连接,通过焊接的方式将轭架与轭架铰接头相连,构成A字形钢结构,使软刚臂的整体受力均匀,提高软刚臂的刚度和稳定性。
软刚臂材料选用EH36钢,长度为30 m,宽度为22.6 m。软刚臂结构如图2所示,EH36钢性能参数见表1。图2中,坐标系原点位于轭架铰接头纵摇轴承的销轴中心,X轴正向由坐标原点指向两个压载水舱方向,Y轴正向由坐标原点指向左压载水舱方向。


表1 EH36钢性能参数
3 有限元建模
应用ANSYS Workbench软件建立软刚臂模型,轭架铰接头采用体单元建模,软刚臂中各钢管段采用壳单元建模。轭架铰接头与轭架之间设置多方安全计算接触,在处理体单元与壳单元连接时,计算精度和效率更优[1]。网格划分后软刚臂有限元模型如图3所示。

4 边界及载荷设置
对软刚臂进行静强度分析,在左、右压载水舱吊耳处设置Z向转动约束,释放其余五个空间自由度。在轭架铰接头纵摇轴承处释放Y向转动,约束其余五个空间自由度。由于软刚臂在作业过程中连续运动,水动力计算所提取的系泊力加载后表现为动不平衡状态,因此在强度分析时需要进行惯性释放设置。
在软刚臂的左、右压载舱吊耳处施加载荷,载荷来源于单点系泊作业时左、右压载水舱吊耳处所受到的结构外力。因为软刚臂在工作过程中Y向受力可通过单点系泊系统的风向标运动释放,所以分析中不考虑Y向载荷。软刚臂左、右压载水舱吊耳受力工况见表2。

表2 软刚臂压载水舱吊耳受力工况 kN
5 强度分析结果
应用Workbench软件对软刚臂结构强度进行有限元分析,得到软刚臂等效应力云图,如图4所示。由图4可知,软刚臂最大等效应力为296.18 MPa,小于材料EH36钢的屈服强度(355 MPa),满足强度要求。由于在最大受压工况下的等效应力最大,因此进行软刚臂轻量化分析时,选取最大受压工况的载荷作为结构优化的基准值[2]。

6 优化设计原理
软刚臂结构优化设计的基本原理是通过建立优化模型,在满足设计变量和状态变量要求的条件下进行迭代计算,求得目标函数的最优值。软刚臂结构优化设计流程如图5所示。
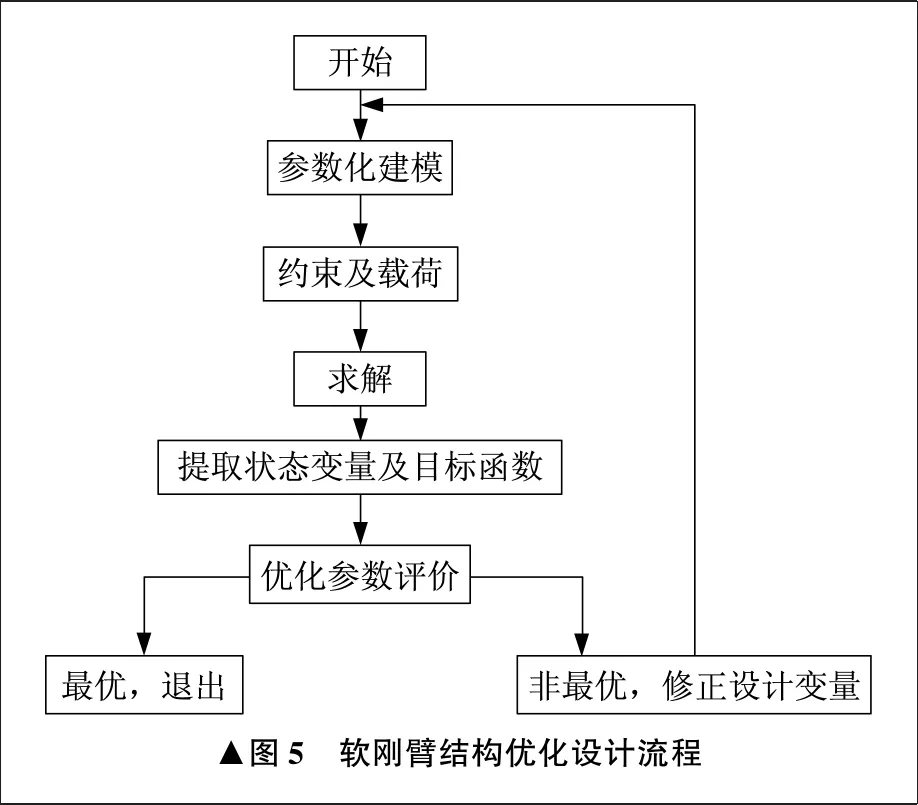
应用ANSYS Workbench软件对软刚臂进行有限元强度分析,得到软刚臂在最大受载时的应力和变形云图,以此确定优化约束条件的基准值。优化设计过程是迭代设计过程,最终收敛于某个确定解。每迭代一次,模型会自动更新,计算结果也会自动更新,迭代参数根据需要可以修改。
采用ANSYS Workbench软件中的快速优化工具,通过设计点的参数来研究输出参数,帮助设计人员在产品设计和使用之前确定各种不同参数对整体结构的影响。优化设计的主要工具包括目标驱动优化、相关参数和响应曲面。目标驱动优化通过多目标优化技术,在给出的样本中得出最佳的设计点[3]。相关参数用于得到输入参数对输出参数的敏感度。响应曲面用于直接观察输入参数对输出参数的影响,通过图表形式动态显示输入与输出参数之间的关系。
7 设计变量与目标函数
在对软刚臂结构进行优化设计时,软刚臂长度和钢管直径保持不变,软刚臂的总质量取决于各钢管段的厚度。将各钢管的厚度作为输入参数,将软刚臂的最大等效应力、最大变形量作为输出参数,将软刚臂总质量最轻作为目标函数。软刚臂各钢管段厚度变量如图6所示,P1为横摇轴承连接筒壁厚,P2为轭架直筒壁厚,P3为轭架斜筒壁厚,P4为锥形连接筒壁厚,P5为压载水舱壁厚,P6为横杆壁厚。优化设计各变量见表3,除P1~P6外,P7为最大等效应力,P8为最大变形量,P9为软刚臂总质量[4]。

在保证迭代精度和可靠收敛的前提下,选用目标函数驱动优化,初始样本数为100。软钢臂模型所有构件材料均为EH36钢,密度相同,因此可将软刚臂总质量最轻作为目标函数。

表3 软刚臂设计优化参数
8 优化结果
应用ANSYS Workbench软件进行优化分析[5-7],设置最大等效应力的上限为355 MPa,基于目标函数的软刚臂结构三种优化设计方案的结果见表4。由表4可知,方案一的软刚臂总质量最轻,是最优设计方案。优化前后变量对比见表5。

表4 软刚臂结构优化设计结果

表5 软刚臂结构优化设计对比
由表5可知,优化后的软刚臂总质量减轻9 390 kg,降幅达4.27%,减少了结构冗余。为观察不同优化设计变量的敏感性,导出优化设计变量对软刚臂最大等效应力、最大变形量和总质量的影响,分析六个输入参数对三个输出参数的敏感性,得到敏感度柱状图,如图7所示。
由图7可知,轭架直筒壁厚对软刚臂最大等效应力的影响最大,是软刚臂的受力最薄弱处。后期进行结构优化时,建议在轭架直筒内部增设加强筋,改善软刚臂的整体受力[8]。

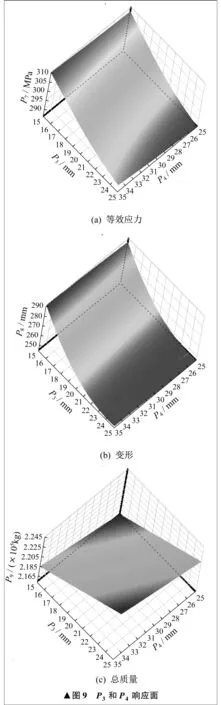
通过Workbench软件中的响应曲面功能,能够更加直观地反映输入参数与输出参数之间的关系。通过响应曲面功能,得到各输入参数与输出参数之间的响应面,如图8~图10所示。


在软刚臂优化设计过程中确认,轭架直筒壁厚对软刚臂的受力影响最大,因此在轭架直筒内设置四组环形加强筋,以改善软刚臂的受力状况[9]。轭架直筒内环形加强筋如图11所示,添加环形加强筋后软刚臂等效应力云图如图12所示。由图12可知,软刚臂最大等效应力为246.74 MPa,相较未添加环形加强筋前的最大等效应力347.02 MPa,减小100.28 MPa。

9 结束语
基于ANSYS Workbench软件中的多目标驱动优化功能,对软刚臂结构进行了轻量化设计。优化后软刚臂总质量减轻9 390 kg,降幅达4.3%。添加环形加强筋前软刚臂最大等效应力为347.02 MPa,添加环形加强筋后最大等效应力为246.74 MPa,减小28.9%。通过建立参数化模型,能够准确观察不同输入参数对软刚臂结构应力和变形的影响情况,与传统软刚臂结构设计相比,能够更加有效地利用材料特性,系统性地减少结构冗余,实现软刚臂结构的轻量化[10-13]。
