堆载工况下软土盾构隧道衬砌纵向力学性能研究

2020-04-22王烨晟罗宇勤张雄健辉俞国骅

华南地震 2020年1期

吴勇王烨晟丁智罗宇勤张雄健任辉俞国骅

（1.中国电建集团华东勘测设计研究院有限公司，杭州 311122；2.浙江省智慧轨道交通工程技术研究中心，杭州 311122；3.浙江华东工程安全技术有限公司，杭州 311122；4.浙江大学城市学院土木工程系，杭州 310015）

0 引言

伴随着我国经济的快速发展和城市化进程的不断推进，地面交通问题持续恶化，地下轨道交通已成为我国诸多大城市发展公共交通时的共同选择，特别是沿海软土地区的一些大城市，如上海、广州、杭州等。地铁建成运营后，伴随着临近建筑活动的展开，地铁上方地表堆载（文中堆载皆视为堆土荷载）乃至超载现象屡见不鲜。

地表堆载对地铁盾构隧道带来严重危害：使隧道产生差异沉降，管片纵缝在内侧或外侧张开，管片间环缝张开，造成隧道漏水，甚至引起泥沙涌入，致使差异沉降更加悬殊，进而导致螺栓应力过大，使纵缝内外侧混凝土产生应力集中，造成角部混凝土开裂脱落。不仅导致了隧道管片渗水问题，甚至会造成隧道结构破环，给隧道运营埋下了严重的安全隐患。

如南京地铁2号线马群至金马路区间，由于渣土过渡堆载引起长达50 m的隧道出现了变形。上海地铁二号线东延伸创新中路站一华夏东路站区间隧道上覆堆载20 m，实测最大水平收敛值达到19.4 cm，隧道结构严重变形。2008年12月，上海某地铁盾构隧道区间地面突发大量堆土，最大堆高达7.0 m，引起了严重的渗漏水及结构损伤病害，部分衬砌环甚至出现顶部混凝土块状脱落及螺栓断裂现象。2014年，上海地铁沿线突发堆土多达16次，引起隧道各类结构及运营安全问题。

针对上述问题，国内外学者展开了相关研究。魏纲[1]等采用Boussinesq公式求解得到地面堆载工况下隧道轴线处的土体附加应力通过算例分析，研究堆载面荷载、堆载偏移距离、隧道上部覆土厚度以及堆载尺寸对隧道纵向位移的影响；魏新江[2]等提出一个以剪切错台为主、刚体转动为辅的隧道变形模式，结合最小势能原理推导出隧道纵向变形量、环间错台量、环间转角和环间剪切力的计算公式。王如路[3]等研究了隧道横向变形随堆载的变化发展规律，建立了隧道变形量的几何简易分析方法，以判断隧道变形状态。

孙文波[4]使用有限元软件MIDASGTSNS对隧道结构变形进行三维数值模拟，分析了既有盾构隧道在附近地面堆载情况下堆载位置与隧道埋深对盾构隧道管片变形的影响；孙廉威[5]等采用连续体有限元模型分析堆载引起的附加应力，并提取应力调整系数，将盾构隧道每环拼装结构等效为均质圆环、环与环之间采用螺栓连接，进行应力叠加三维荷载－结构分析；张明告[6]等利用有限元模型，模拟监测堆载下隧道结构变形情况，分析了不同竖向土压力和不同土质条件等对隧道结构变形的影响，结果表明隧道穿越土层及上覆土层的压缩模量是影响地表堆载作用造成不同竖向土压力，进而导致隧道结构产生不同程度变形的主要原因。

马忠政[7]对隧道收敛变形的现场监测数据进行分析，并建立数值计算模型对从隧道施工前的堆载到施工完成后的卸载全过程进行模拟。结果表明隧道施工前的地面堆载对隧道收敛变形具有显著影响；邵华[8]等利用上海某地铁在地表堆载下隧道的监测数据，对比了上覆堆载高度与隧道沉降及衬砌水平直径的变化关系；吴庆[9]和张明告等利用室内模型试验的实测结果，结合数值模拟及工程实例分析了地表堆载对隧道结构变形的影响因素，结果表明隧道穿越土层的土质条件、隧道埋深、堆载高度及堆载相对隧道的位置等是影响隧道变形的主要因素。

上述研究主要针对隧道的外在变形如隧道沉降、衬砌张开量等进行研究，此外数值模拟的研究结果仅与实际定性分析结果相符，在定量分析时仍存在较大偏差。上述研究并未针对堆载工况下隧道衬砌内在力学性能的变化，提出相应的加固方案。

隧道上方过度堆载引起隧道衬砌变形，大大降低了衬砌整体的力学性能。志波由纪夫等在大量研究的基础上，提出纵向等效连续化模型[10]。该模型将衬砌横截面简化为均质圆环，将有接头和管片组成的盾构隧道等效为纵向刚度等性质均一的连续梁。但事实上，盾构隧道管片是由螺栓连接，而螺栓与管片的刚度差异较大，管片环缝处是隧道整体刚度的薄弱点。而且在实际工况下，螺栓的特性、环缝的影响范围和管片的横向变形等都会对隧道的纵向等效抗弯刚度产生影响。

本文在志波模型的基础上进行改进，同时考虑衬砌横向变形以及管片之间螺栓连接效应的情况下，推导堆载作用下衬砌纵向等效抗弯刚度及极限弯矩的计算公式。

1 理论推导

本文针对现有研究的不足，理论推导堆载工况下隧道衬砌纵向等效抗弯刚度及其极限弯矩的计算公式，创新性地引入纵向等效抗弯刚度折损率 η（EI）eq和极限弯矩折损率 ηMy的概念，并结合室内模型试验的结果，分析总结堆载工况下隧道衬砌的力学性能变化规律。根据 η（EI）eq和 ηMy的变化情况提出相应的隧道加固方案。图1、图2分别为隧道上方堆载衬砌变形示意图和管片环轴向变形示意图。

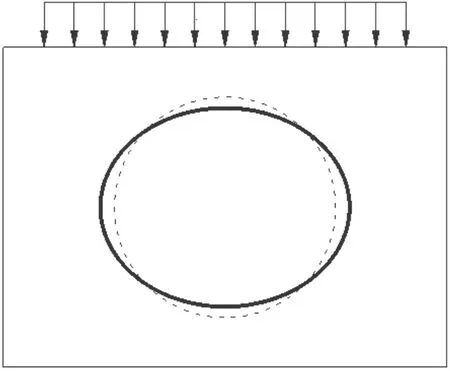
图1 堆载下衬砌变形图Fig.1 Lining stacking deformation diagram under heap loading

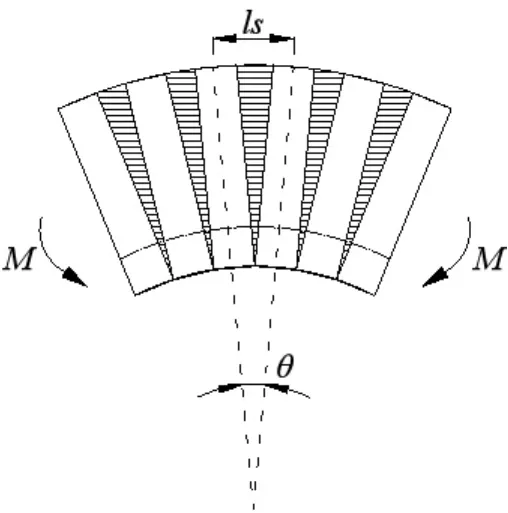
图2 隧道轴向变形图Fig.2 Tunnel axial deformation diagram

1.1 基本假设

（1）隧道穿越土层土质均一。

（2）管片发生转动，受拉区由混凝土和连接螺栓共同承担拉力且螺栓一直处于弹性状态；受压区由混凝土单独承担压力且受压混凝土始终处于弹性状态。

（3）截面变形符合平截面假定和小变形假定。

（4）连接螺栓受拉用弹簧受拉模拟，环缝的张开量等效为螺栓的拉伸量。

（5）以两相邻管片环的中心线间距ls为一个计算单元，螺栓的收拉长度为其本身长度lb，管片的受压长度为整个单元长度。

1.2 计算模型

根据实际工况下，隧道衬砌横截面在堆载作用下其圆形截面产生 “横鸭蛋”变形，建立如图3所示隧道衬砌横截面计算模型。

图3横截面变形图Fig.3 Cross section deformation diagram

图3 中a、b分别为椭圆的长轴和短轴；c为中性轴到水平对称轴的距离；φ为中性轴衬砌上一点和原点连线与水平对称轴的夹角。在管片上取微单元ds，其到椭圆圆心的距离r可近似取（a+b）/2，dα是微单元所对应的圆心角，α为微单元和原点连线与椭圆竖向对称轴的夹角，x为微单元到中性轴的距离。

1.3 考虑横向变形的纵向等效抗弯刚度及极限弯矩计算

图4为堆载下衬砌应力应变状态。

此时ds满足式（2），ds处于衬砌受压侧（即中性轴以下）：

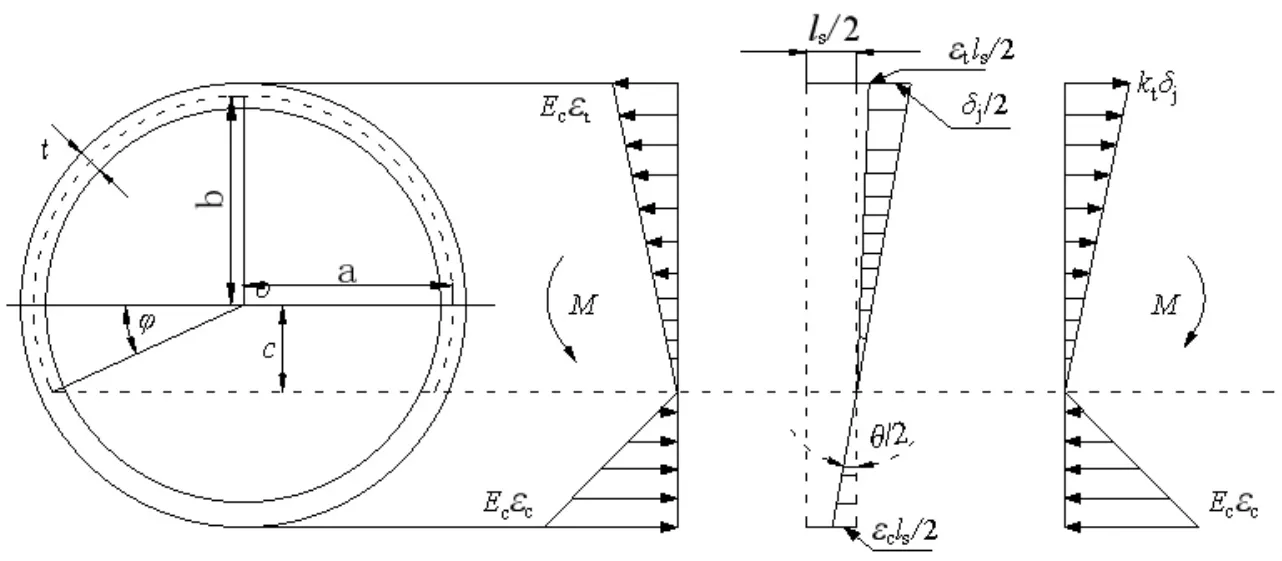
图4 衬砌应力应变图Fig.4 Stress-strain diagram of lining

ds处于衬砌受拉侧（即中性轴以上）：

由变形协调条件可得受拉侧螺栓的最大变形量δt和受压侧管片的最大变形量δc：

式中θ为截面转角。

由力的平衡条件得：

结合变形协调条件，得φ满足：

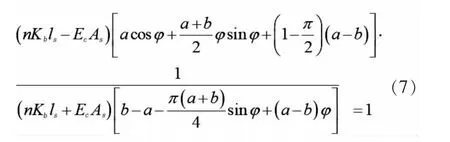
由弯矩平衡条件得：

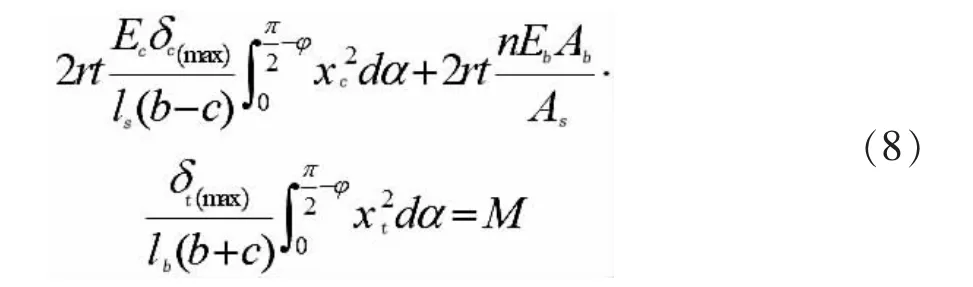
式（8）中：Ec和Eb分别为管片的弹性模量和螺栓的弹性模量；As和Ab分别为隧道的横截面面积和螺栓横截面面积；n为纵向螺栓数量；t为管片厚度；Kb为单个螺栓的弹性刚度。

假设：

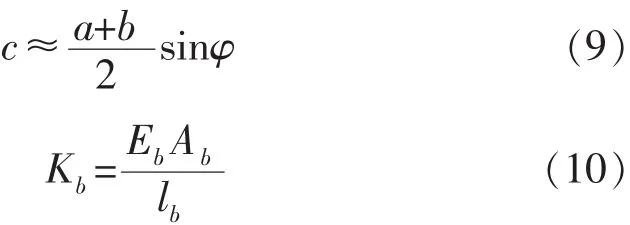
将式（2）、（5）、（9）、（10）代入式（8），得：

纵向等效连续化模型在M相等时其转角为：

由式（12）、（13）解得：

式（14）中，（EI）eq为纵向等效抗弯刚度。

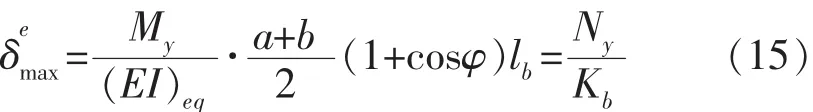
式（15）中，Ny为螺栓的弹性极限拉力。由式（15）可得：

考虑螺栓预应力N0的影响：

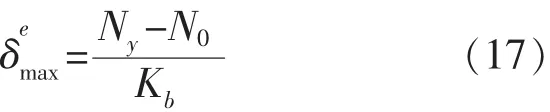
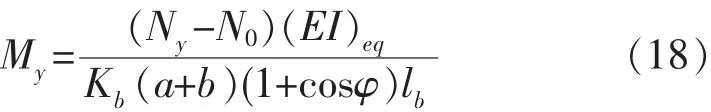
2 堆载工况下隧道性能分析

表1为某盾构隧道的主要结构参数，本文利用该参数计算分析隧道上覆堆载对隧道性能的影响。

2.1 隧道衬砌等效抗弯刚度及极限弯矩计算

衬砌在标准状态下，竖向直径和水平直径相同，即a=b=2.925 m。

将表1中参数代入式（10），得单个螺栓的弹性刚度Kb=3.534*105 kN/m，将Kb代入式（7）得φ=55°，进而可以求得 ψ1=0.185， ψ2=64.260，将 ψ1和ψ2代入式（14），即可求得弹性状态下管环的纵向等效抗弯刚度（EI）eq=6.640*107 kN/m2，将其带入式（18）的螺栓在弹性状态下可以承受的最大弯矩My=6.990*105 kN·m。

根据现有地铁设计规范，可将地表堆载等效为隧道上覆土层[12]，本文基于文献 [6]室内模型试验（如图5所示）的结果，整理取得隧道上覆堆载高度h和与其相对应的隧道水平及竖向直径数值。如表2所示，其中D=5.85m。

表2 隧道上覆堆载高度h和与其对应的a、b值Table 2 The heap height of tunnel h and its corresponding a and b values

将表2数据代入公式计算，计算结果如表3所示。

2.2 隧道性能分析

图6、图7分别为隧道上覆堆载高度与纵向等效抗弯刚度及隧道极限弯矩的变化关系曲线图。从图中可以发现：随着隧道上覆堆载高度的增加，隧道的纵向等效抗弯刚度及其极限弯矩呈明显下降趋势即隧道的纵向等效抗弯刚度及其极限弯矩随隧道上覆堆载高度的增加而减小，且纵向等效抗弯刚度呈线形减小，极限弯矩呈抛物线减小

图5 堆载下衬砌变形图模型试验[6]Fig.5 Model test of lining deformation under heap loading

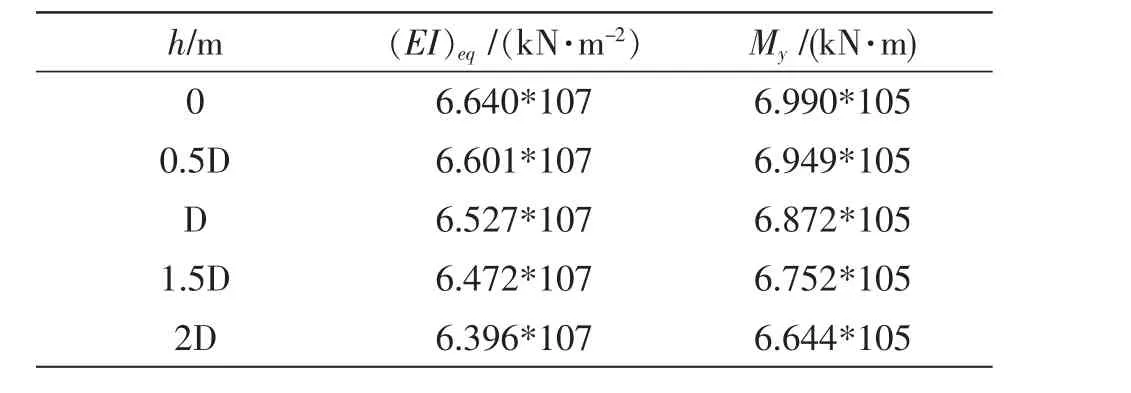
表3 不同上覆堆载高度下衬砌的纵向等效抗弯刚度及其极限弯矩Table 3 Longitudinal equivalent flexural stiffness and limit moment of lining under different overburden heap height

图7 隧道上覆堆载高度与衬砌极限弯矩的关系曲线Fig.7 Relationship between overburden heap height and lining limit bending moment

上覆堆载高度与衬砌纵向等效抗弯刚度的关系拟合公式为：

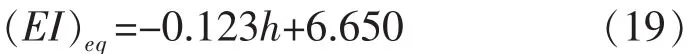
上覆堆载高度与衬砌极限弯矩的关系拟合公式为：

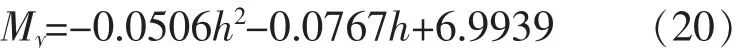
为了更直观地呈现隧道上覆堆载高度与衬砌纵向等效抗弯刚度和极限弯矩的关系，本文引入新的概念：纵向等效抗弯刚度折损率η（EI）eq，即衬砌纵向等效抗弯刚度随上覆堆载高度增加的减小量与原值之比；极限弯矩折损率ηMy，即衬砌极限弯矩随上覆堆载高度增加的减小量与原值之比。

上覆堆载高度与衬砌纵向等效抗弯刚度折损率的关系拟合公式为：

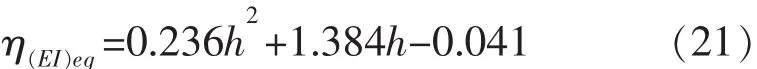
上覆堆载高度与衬砌极限弯矩折损率的关系拟合公式为：

假设无堆载工况下折损率为零，对上述公式分别进行修正：

如图8所示，虚线为修正前曲线，实线为修正后曲线。堆载高度为0.59 D时，衬砌纵向等效抗弯刚度折损率和极限弯矩折损率均为0.900%，可以发现在隧道上覆堆载高度不超过0.59 D时，衬砌纵向等效抗弯刚度折损率和极限弯矩折损率变化量基本一致。上覆堆载高度大于0.59 D后，随着堆高的增加极限弯矩折损率增值速率明显超过纵向等效抗弯刚度折损率增值速率。但从两者的增值趋势来看，都呈抛物线型增长，且其切线斜率增长较快，因此隧道上覆堆载过大，将大大降低衬砌的力学性能，严重时将造成衬砌破损，给隧道运营带来严重的安全隐患[14-15]。

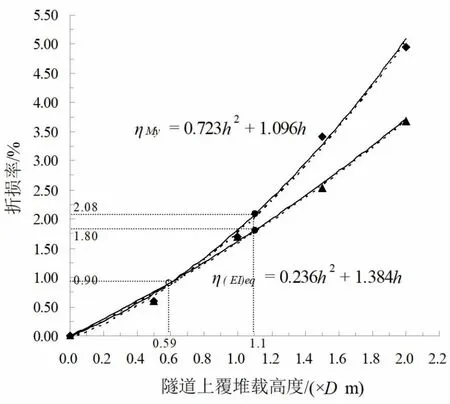
图8 衬砌纵向等效抗弯刚度和极限弯矩折损率关系曲线Fig.8 The relationship between the longitudinal equivalent bending stiffness and ultimate bending moment damage rate

本文根据衬砌纵向等效抗弯刚度折损率和极限弯矩折损率的变化，采用不同的方式对隧道进行加固。结合顾春华[15]提出的隧道结构加固原则：首先粘贴芳纶布对隧道进行临时加固，然后采用钢圈支护补强。针对横向变形介于10 cm和12 cm的管片，进行半环安装；横向变形大于12 cm的管片，进行整环安装，本文建议：当堆高≤0.59 D，衬砌纵向等效抗弯刚度折损率和极限弯矩折损率都不超过0.9%时，采用芳纶布对隧道衬砌进行加固；当0.59D＜堆高＜1.10D，衬砌纵向等效抗弯刚度折损率小于1.8%,极限弯矩折损率小于2.1%，建议采用芳纶布结合钢环半环加固衬砌；当堆高≥1.10D，衬砌纵向等效抗弯刚度折损率超过1.8%，建议采用钢环整环加固衬砌。

3 成果应用

3.1 既有隧道堆载概况

杭州地铁1号线彭埠站—建华站及彭埠站—七堡出段线盾构区间位于江干区彭埠镇，彭埠站—建华站区间左线长约1529 m，右线长约1622 m，隧道埋深6~25 m；彭埠站—七堡出段线区间长约650 m，隧道埋深约4.5~9.5 m。

盾构隧道竣工完成后，2011年5月施工方发现已建成盾构保护范围内有社会车辆弃土，随即向地铁公司发函表明要立即卸载，以防地面超载引起管片变形过大，避免发生工程事故。堆土位于泸杭高速西侧白石村地块，堆土高度5~10 m，范围长达260 m，与区间受损管片范围一致（图9）。由于两区间上部堆载，土体固结产生沉降。加载及沉降导致隧道变形，道床与隧道脱开，管片发生不同程度的碎裂。

图9 隧道上覆堆载平面示意图Fig.9 The schematic plan view of overburden

3.2 隧道加固

现场观测彭埠站—建华站区间联络通道两侧10环范围内横向收敛变形达到109 mm，其管片状态不稳定处于发展状态。结合本文研究成果可估算出该范围衬砌纵向等效抗弯刚度折损率和极限弯矩折损率分别约为3.65%和4.98%。根据前文提出加固意见，采用钢环整环加固衬砌。区间内其余收敛变形大概为50~60 mm。此部分区间衬砌纵向等效抗弯刚度折损率为1.31%~1.68%，极限弯矩折损率为1.41%~1.89%。根据前文提出加固意见，采用芳纶布结合钢环半环加固衬砌。