基于马尔科夫链的裂缝期次分析——以重庆天府地区上二叠统长兴组露头为例

袁 帅， 胡 明,3*， 李 瑞， 王 豪， 胡 峰

(1.西南石油大学地球科学与技术学院，成都 610500；2.中国地质大学构造与油气资源教育部重点实验室，武汉 430074；3.天然气地质四川省重点实验室，成都 610500；4.东方地球物理公司西南物探分公司，成都 610213)

裂缝研究对于了解岩体强度、岩体变形性、岩体稳定性、流体流动、油气储集与开采、断裂机制和构造历史至关重要[1]。目前有多种研究构造裂缝发育期次的方法,其中基于岩心资料的裂缝观察、裂缝充填物同位素分析、包裹体测温、岩石声发射等方法都是研究裂缝期次的有效方法。然而，由于裂缝具有多期成因、多期改造、多期充填的特点，每一种技术方法都具有一定的局限性或多解性[2]，且实验方法涉及采样、制样等繁琐的实验步骤，对样品、操作以及设备的要求极高，费用相当昂贵且容易出现误差。外国学者以概率学为理论基础提出了一种基于马尔科夫链的时间顺序研究方法，这种方法曾用于沉积学中地层旋回模式、复理石韵律结构等研究[3-6]，Snyder将其公式修改之后首次运用到裂缝期次的研究之中[7-8]。为此，在前人的研究基础之上，以重庆天府地区上二叠统长兴组大量出露的裂缝为研究对象，用马尔科夫链分析该地区的裂缝发育期次,再利用裂缝充填物碳氧同位素测试结果对结论加以验证，意在为日后油气勘探或基础地质研究提供一种经济有效的裂缝期次研究方法。

1 研究区概况

1.1 地质概况

研究区(图1)位于重庆天府地区，研究对象为观音峡背斜核部或靠近核部的长兴组地层。观音峡背斜是川东高陡褶皱带西南方向的分支。整体呈北东-南西向延伸，出北碚后转向南延，经中梁山后转向东南伸达九龙坡，被长江切穿轴部，过江以后逼近綦江而倾伏。背斜为两翼不对称的斜歪褶曲，轴面倾斜(先东南倾斜，后西北倾斜)，轴线扭转弯曲(反“S”形)，枢纽鞍状起伏[9]。

1.2 裂缝发育特征

裂缝的基本参数包括裂缝的宽度(张开度)、长度、间距、密度、产状、充填情况以及溶蚀改造等[10]。通过大量的野外观察和测量，发现本地区天然裂缝极为发育，主要以构造成因的张性裂缝为主[图2(a)]，裂缝面较为粗糙且不平整，有少量的X形剪切缝[图2(b)]以及雁列式节理组[图2(c)]；裂缝面较宽(即张开度较大)，可高达3～4 cm，且充填情况较好，充填深度可达20～25 cm[图2(d)]；单条裂缝长度最长可达20～30 cm，而最短不过数厘米；裂缝发育较为密集，平均为5条/m；由于靠近背斜转折端，裂缝所在岩层产状均较为平缓，倾角为20°～30°，且裂缝多为高角度裂缝或垂直缝；研究区裂缝发育多而杂乱，交切关系复杂，没有明显的交切关系能说明裂缝发育期次，但总体而言有四个优势方位，分别是北东向、近东西向、南东东向以及南南东向(图3)。

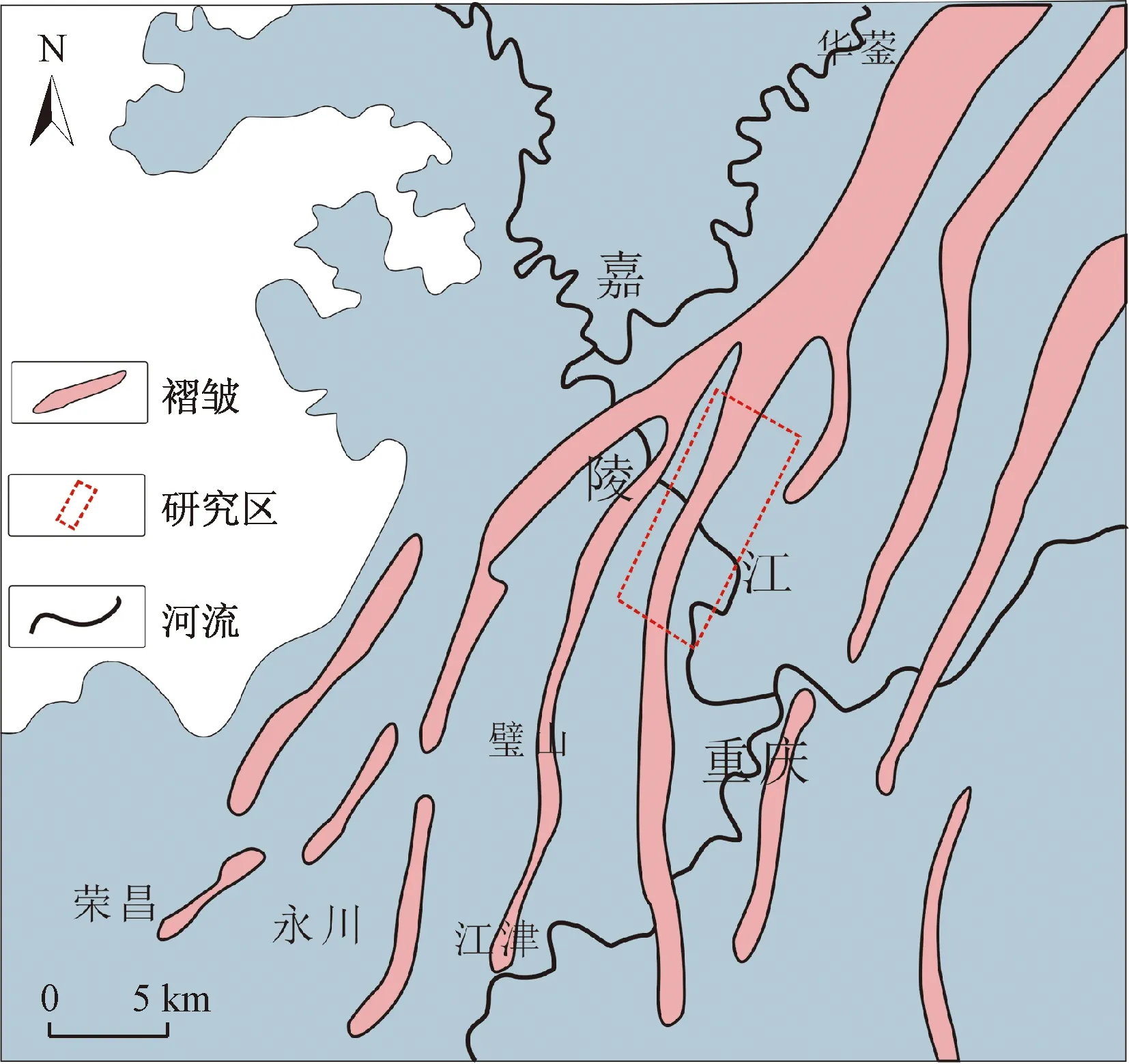
图1 研究区地理位置图

图2 研究区裂缝特征

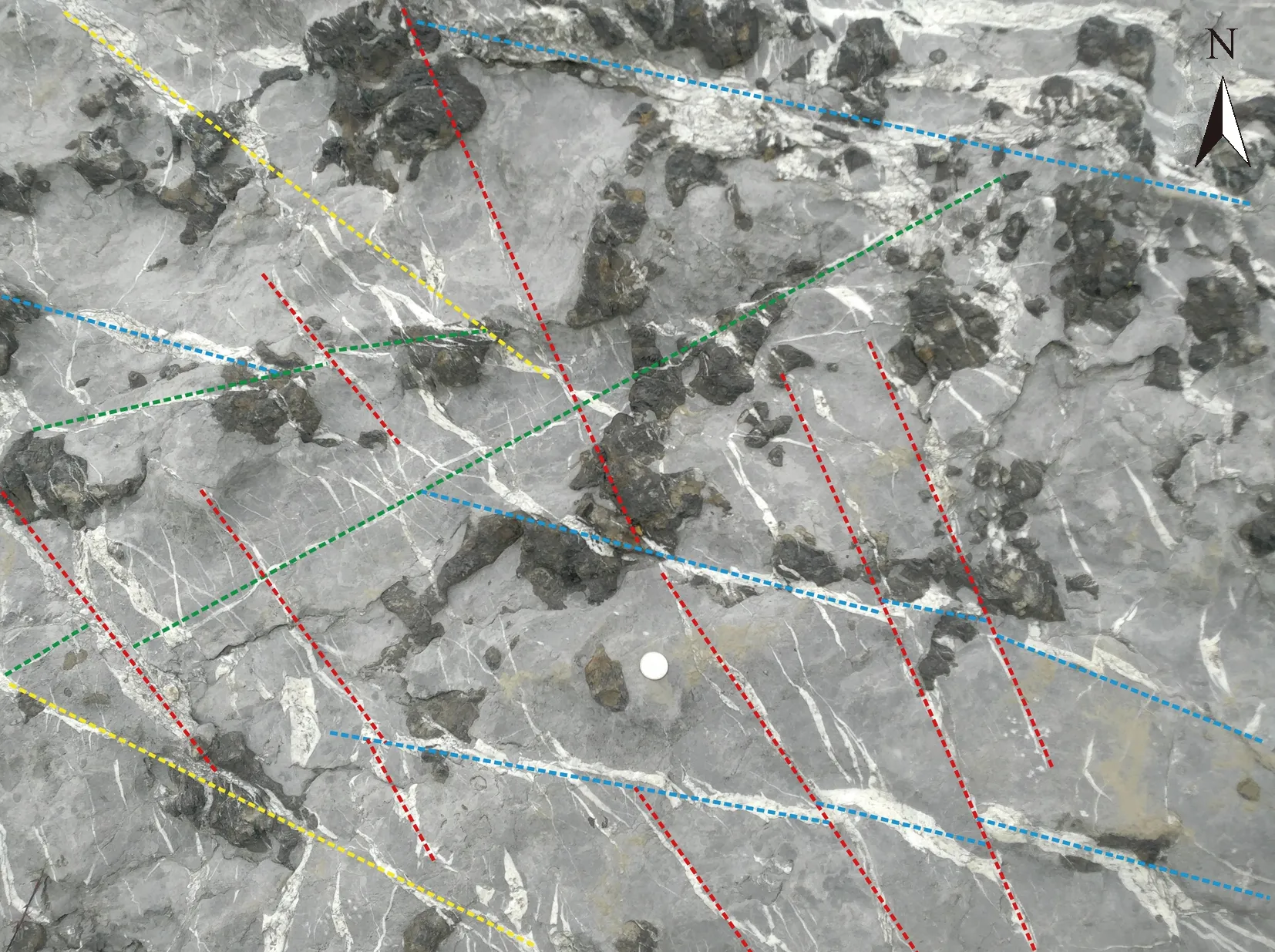
图3 研究区裂缝露头及主要方向

2 马尔科夫链综合分析

野外观察发现，裂缝展布极为复杂，无法简单地根据若干条裂缝之间的分期配套得出整个区域的裂缝发育期次，因此需要一种方法来判断是否某一方向的裂缝频繁地与其他方向裂缝显示出时间的先后关系，从而评估研究区裂缝的发育期次。马尔科夫链就是这样一种研究时间序列中事件之间关系的统计方法。

当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态，称这个随机过程具有马尔可夫性质，是一个马尔科夫过程[11]。地质过程的马尔科夫链模拟作为地质分析的一种手段，其有效性已经被中外地质界所应用。构造裂缝的形成就是一个随机过程，且下一条裂缝的状态概率分布仅与当前裂缝有关，与上一条裂缝无关，因此理论上该随机过程具有马尔科夫性质，可使用马尔科夫链进行研究。

2.1 基本方法

马尔科夫链是一个基于概率统计的方法，在运用到裂缝研究中时，先通过大量的野外观察和测量，将各个方向裂缝之间的时间先后关系统计到矩阵(实际转移频数或观测值)，再通过公式计算出一个随机的时间先后关系(随机转移频数或估计值)，最后计算两者的标准化残差。意在通过标准残差值来对比是否某一方向的裂缝会比预期更频繁地与另一方向的裂缝产生时间关系，并最终得出一个总体的时间序列。具体方法如下。

(1)数据准备：马尔科夫链分析是一种统计学方法，对样本数据的准确度有着较高的要求，如何减少样本数据采集时的误差是必须要考虑的问题，现采用圆形测线法来收集样本数据[12]:在研究区地层露头上用粉笔画直径为1 m的圆，然后记录圆内裂缝的产状，交切关系等特征(图4)。由于研究区地层较为平缓(岩层倾角均小于20°)，则可不考虑岩层对裂缝产状测量的影响。研究共使用测线50组，测得裂缝797条，记录了346次交切关系。

地层中展布的各个时期形成的裂缝称之为状态，某一时刻裂缝从一种状态转移到另一种状态，称之为状态转移。状态的选择是应用马尔科夫链分析的关键。状态的选择要考虑到实际的裂缝交切关系，若状态区域划分太大，则容易忽略掉同一个区域内裂缝的转移。现以玫瑰花图中显示的“极小值”为边界，分别是25°、65°、95°以及145°，共划分了4个区域(图5)，结合野外观察，设立了四种状态用于马尔科夫链分析，分别是以45°为主的北东向裂缝、以165°为主的南东向裂缝，以80°为主的近东西向裂缝和以120°为主的南东东向裂缝，其中北东向裂缝和近东西向裂缝虽发育数量较少，但与其他裂缝之间存在时间关系，故为不可忽略的状态。

(2)转移频数：根据裂缝的交错和限制关系，将某一方位的裂缝晚于另一方位裂缝的次数作为转移频数，并记录在表格中(表1)，其纵列表示较晚的裂缝，横列表示较早的裂缝(如表1中B行A列(记作OB,A)数据表示B区域的裂缝晚于A区域的裂缝的次数为1次)，并将总的转移频数记录在表格的最右下角。

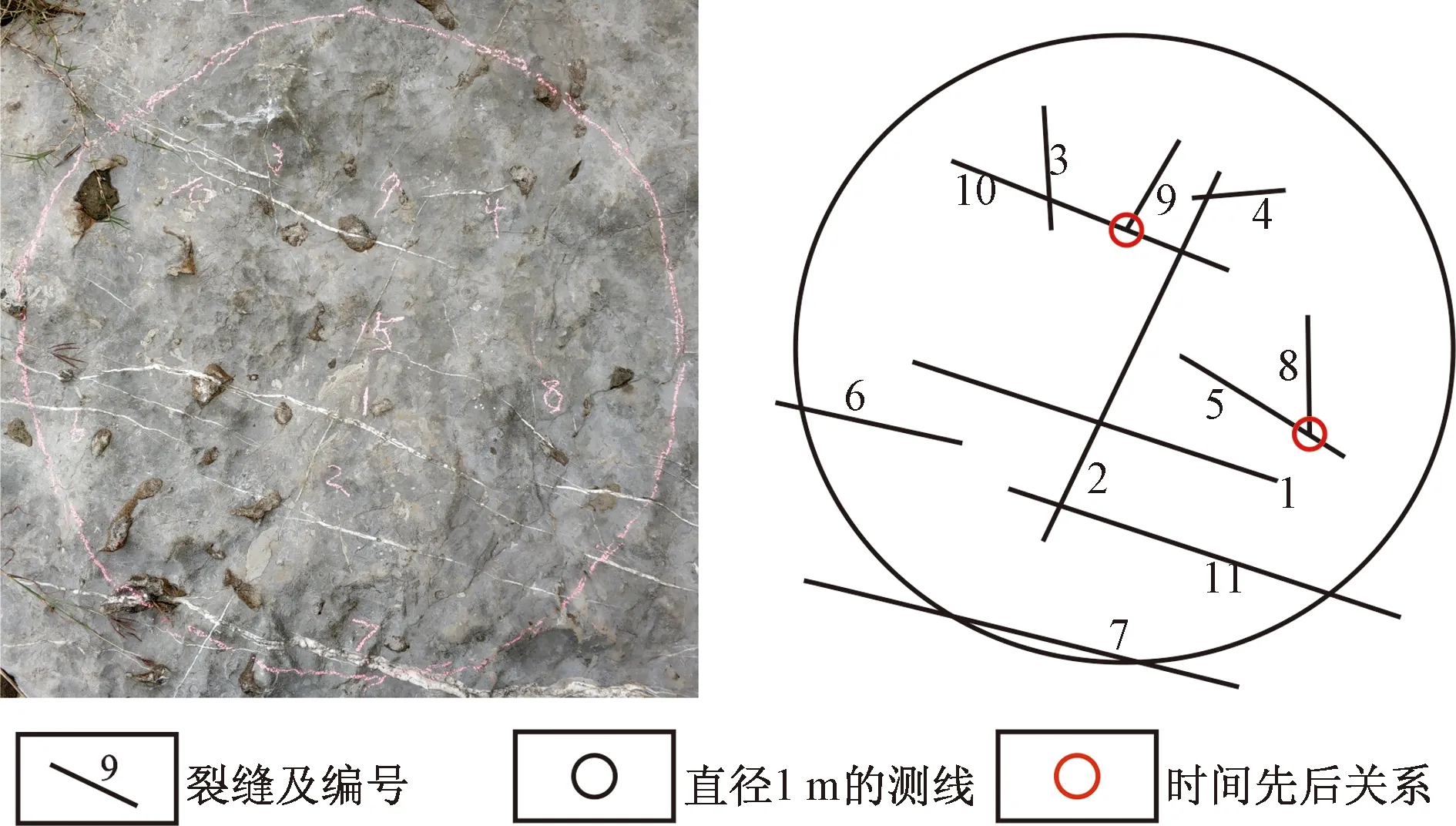
图4 使用圆形测线的野外数据统计

图5 节理玫瑰花图及分区

表1 转移频数矩阵

在计算出系统的状态转移频数矩阵的基础上，检验该系统是否具有马尔科夫性质可选用统计量x2进行假设检验。Snyder根据Cochran的理论进行x2检验[13]，然而这一检验方法并没有结合马尔科夫链的特征，现在前人研究的基础上对检验方法进行改善[14]，采用公式：

(1)

式(1)中：fij为转移频数矩阵的值；pj为转移频数矩阵第j列之和除以总转移频数的值，称为边际概率；pij为fij除以总转移频数的值，即转移概率(表2)。

(3)随机转移值计算：根据观测的实际转移数据即转移频数，可以计算出状态的随机转移数据。通常情况下，其公式为

EA,B=SASB/N

(2)

式(2)中：EA,B为A行B列的随机转移值；SA为A区域观测到的总时间关系数；SB为B区域观测到的总时间关系数，N为所有测线内时间关系总数。

然而裂缝之间的角度关系影响着裂缝之间的交切次数，如在一个固定区域内，相互垂直的裂缝会比斜交的裂缝出现更多的交切次数(图6)，因此需要将随机值乘以一个因子sin(|θA-θB|)以减小角度对交切关系的影响。修改后的公式为

表2 转移概率矩阵

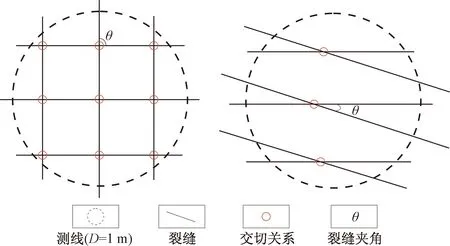
图6 角度关系对交切次数的影响[7]

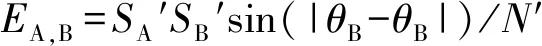
(3)

式(3)中：SA′为A区域总的裂缝数；SB′为B区域总的裂缝数；θA为A区域中点的方位角度数；θB为B区域中点的方位角度数；N′为测线中观测到的总的裂缝数。

再将所得随机数据乘以N/SE(SE为随机数据之和)，使随机数据之和等于观测数据之和，以便于下一步的残差对比，计算结果见表3。

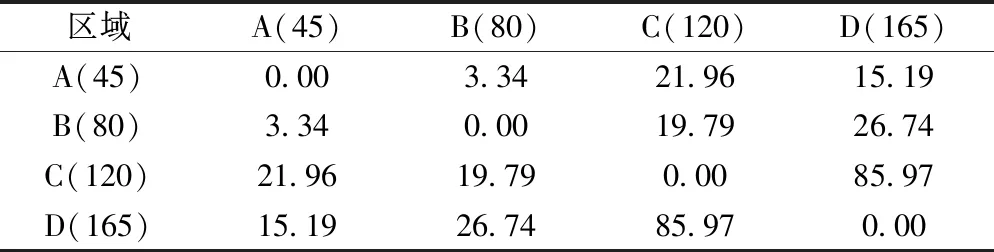
表3 随机数据矩阵

(4)标准残差计算：标准化残差指的是观察值与随机值之差的标准化，突出的是表示观测值偏离随机值的程度(表4)。计算时利用公式：

(4)

式(4)中：RA,B为标准残差值；OA,B为A行B列的转移频数；EA,B为A行B列的随机转移值。

在本研究中，其值表示某一方向裂缝比随机值更频繁或者更少晚于另一方向裂缝的程度。根据标准残差表，比较表格中斜对角正负相反的单元值来确定相对的时间。如果一个单元格值为正，而斜对角的值为负，那么这一对的列模式就发生在行模式之前(如D行C列值为正值而其对角线C行D列为负值，则D行所代表的以165°为主的裂缝晚于C列中以120°为主的裂缝)。在进行这些比较时，若对角单元格的标准残差值均为负值，则这组值没有任何意义。

2.2 结果分析

根据标准残差表中所得数据(表4)，A区域和B区域(A行B列和B行A列)对应的值分别是-1.83和-1.28，均为负值，为无意义数据；A区域与C区域对应的值分别是0.43和-2.13，表示A区域裂缝形成时间晚于C区域裂缝；A区域与D区域对应的值分别是-1.59和-0.82，无意义；B区域与C区域对应的值分别是-0.85和3.19，表示C区裂缝形成时间晚于B区裂缝；B区域与D区域对应的值分别是-2.46和5.08，表示D区域裂缝形成时间晚于B区域裂缝；C区域与D区域对应的值分别是-3.66和3.56，表示D区域裂缝形成时间晚于C区域裂缝。

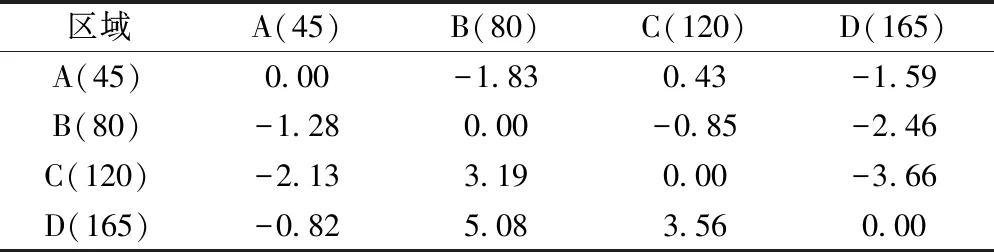
表4 标准残差表

根据上述结论得出裂缝形成的时间顺序(图7)：以80°为主的近东西向裂缝为最早生成的，其次是以120°为主的南东东向裂缝，以165°为主的南南东向裂缝和以45°为主的北东向裂缝没有明显的先后关系，推测为同期生成，结合野外裂缝观察，这两组裂缝可能是一对X形共轭剪切缝或是在形成时期扭动而成。

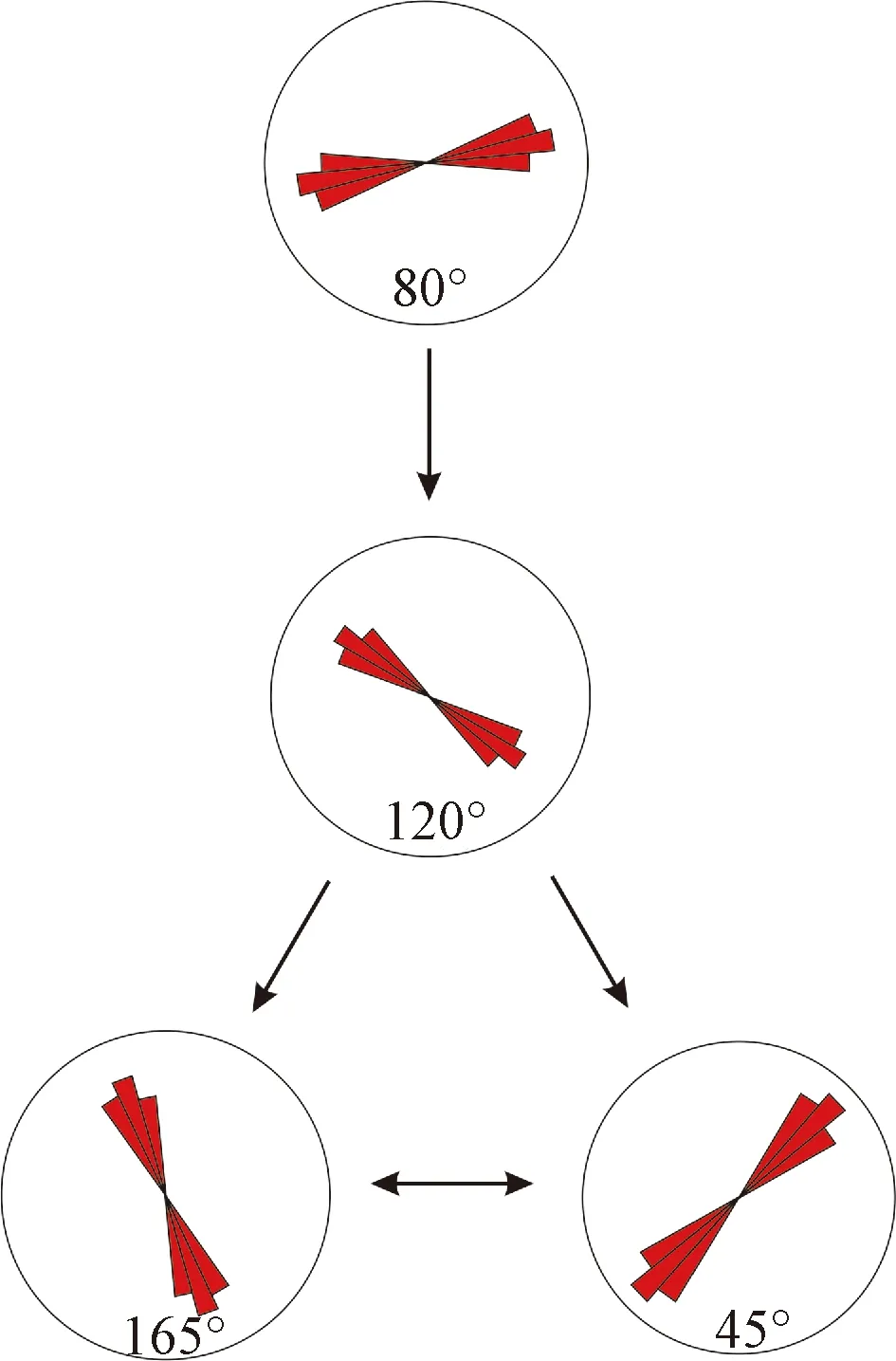
图7 裂缝形成的时间顺序

3 充填物碳氧同位素特征

裂缝充填物碳、氧同位素分析也是划分裂缝形成期次常用的方法。当地层水进入裂缝时，或多或少有结晶矿物析出并沉淀在裂缝壁上，结晶方解石时的古地温、古水介质条件和有机碳的影响决定了碳、氧同位素的丰度，不同时期充填物的碳、氧同位素值必然不同[15-19]。由于研究区裂缝方解石充填程度较好，因此用该方法分析研究区裂缝发育期次，从而对上述结果进行验证。

裂缝的形成过程属于“真空扩容”过程，饱和地层水在第一时间进入裂隙中，必然在缝壁富集，受到多期矿化水影响，可能存在多期胶结物。因此，在研究裂缝形成期次时，采集的裂缝充填物必须是靠近缝壁的，且只能对第一期充填的次生矿物进行分析[20]。此次实验严格选取各期次裂缝对应的充填物，采样时避开被风化的缝面充填物，采深层靠近缝壁的新鲜充填物进行同位素分析，结果如图8所示。第一期裂缝充填物的δ18O和δ13C集中在Ⅰ区，δ18O平均值为-8.58‰，δ13C平均值为3.32‰；第二期裂缝充填物的δ18O和δ13C集中在Ⅱ区，δ18O平均值为-7.16‰，δ13C平均值为3.79‰；第三期裂缝充填物的δ18O和δ13C集中在Ⅲ区，δ18O平均值为-5.18‰，δ13C平均值为3.70‰。研究区裂缝充填物δ18O和δ13C的集中分布在3个区域内，因此，判断裂缝有3个形成期次。

图8 裂缝充填方解石碳氧同位素分布图

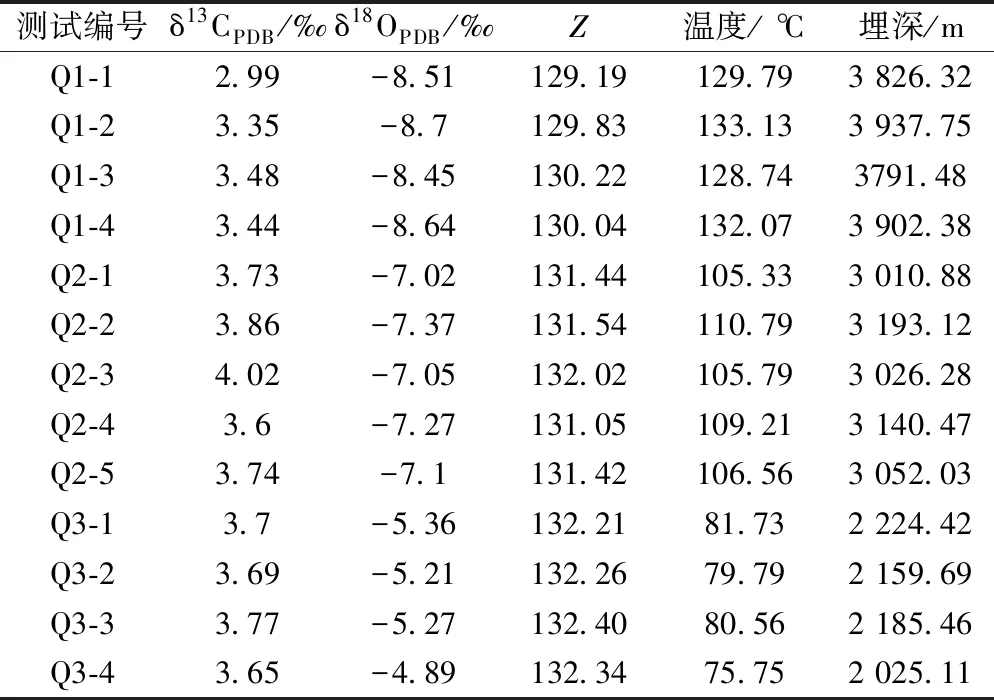
为进一步分析充填物的形成时期，根据前人的研究方法计算了其盐度指数Z、形成温度以及埋深(表5)。根据Weber(1964)公式计算其Z用于区分成岩环境[21-22]，计算公式(Peedee Belemnite,即PDB标准)为

Z=2.048(δ13C+50)+0.498(δ18O+50)

(5)

Z在120以上的碳酸盐岩应归入海水成因环境，Z在120以下的应归入淡水成因环境。碳氧同位素中的氧同位素可以指示充填物形成时的古温度，现采用Epstein等[23]提出的氧同位素测温方程来计算充填物充填时的温度，其方程式为

T=31.9-5.55(δ18O-δ13Ow)+0.7(δ18O-δ13Ow)2

(6)

式(6)中：T为方解石矿物形成时的温度， ℃；δ18O为测定矿物的氧同位素值，‰；δ13Ow为形成方解石矿物时水介质的氧同位素值，‰。

计算时取海水介质δ13Ow为-2‰，可以得出其充填温度，再根据研究区古地表温度(15°)和古地温梯度(3.0 ℃/hm)[24]，可以折算出裂缝形成时的埋藏深度。根据换算，第一期裂缝形成的平均埋深为3 864 m，形成温度为130 ℃;第二期裂缝形成的平均埋深为3 084 m，形成温度为107 ℃;第三期裂缝形成的平均埋深为2 147 m，形成温度为79 ℃。

4 构造演化史及埋藏史分析

结合研究区构造演化史，天府地区上二叠统长兴组地层主要经历了燕山期和喜山期两期构造应力场的作用[25]。燕山时期，受太平洋板块向亚洲板块俯冲的影响，华南板块内部发生了大规模的由南东向北西的推覆作用，产生南东向北西的强烈挤压，从雪峰至江南古陆地区经湘西北至川东，冲断作用的强度逐渐降低，应力传递到天府地区，其区域应力场为北西向，形成了南东东向和近东西向构造裂缝。喜山时期，受太平洋板块俯冲及印度板块向欧亚板块碰撞挤入双重影响，且有扭动活动，产生了北西-南东向构造应力，在此应力的作用下，形成了南南东向和北东向裂缝。

再根据研究区所在地区埋藏史(图9)，第一期裂缝形成时平均埋深为3 864 m，为燕山早期产物；第二期裂缝形成时平均埋深为3 084 m，为燕山晚期产物；第三期裂缝形成的平均埋深为2 147 m，为喜山早期产物。

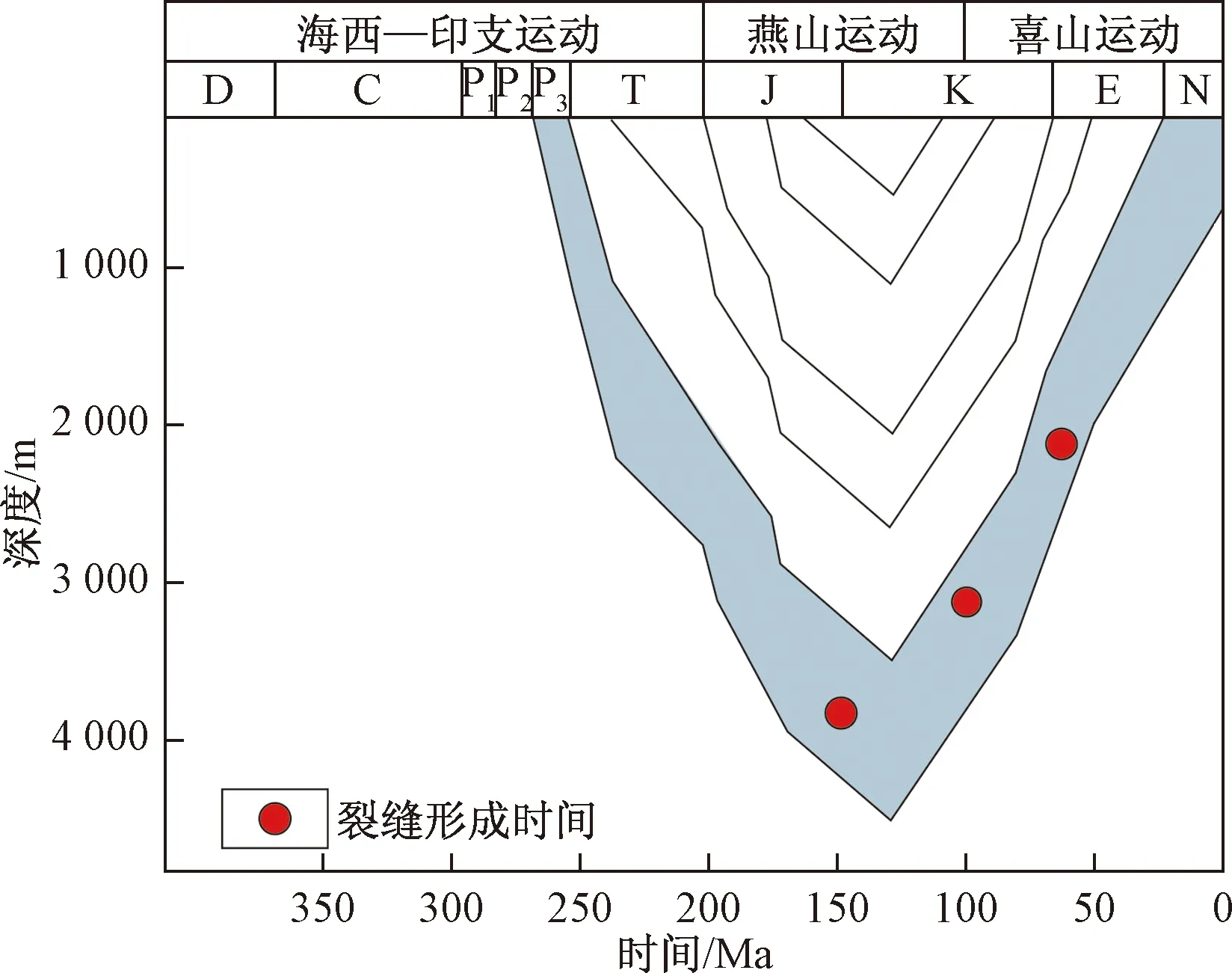
图9 渝西地区埋藏史图[26]

5 结论

(1)根据马尔科夫链分析结果，以80°为主的近东西向裂缝为最早生成的，其次是以120°为主的南东东向裂缝，以165°为主的南南东向裂缝和以45°为主的北东向裂缝没有明显的先后关系，这两组裂缝可能是一对X形共轭剪切缝或是在形成时期扭动而成。

(2)充填物碳氧同位素实验显示，第一期裂缝充填物δ18O平均值为-8.58‰，δ13C平均值为3.32‰，形成时平均埋深为3 864 m，形成温度为130 ℃；第二期裂缝充填物δ18O平均值为-7.16‰，δ13C平均值为3.79‰，形成时平均埋深为3 084 m，形成温度为107 ℃；第三期裂缝充填物δ18O平均值为-5.18‰，δ13C平均值为3.70‰，形成时平均埋深为2 147 m，形成温度为79 ℃。结合研究区构造演化史以及埋藏史，第一期裂缝形成于燕山早期；第二期裂缝形成于燕山晚期；第三期裂缝形成于喜山早期。

(3)充填物碳氧同位素的实验结果成功验证了马尔科夫链的分析，证实马尔科夫链为一种可行的裂缝期次研究方法，可用于日后油气勘探或基础地质研究之中。