基于快速凸包的目标车辆动态围堵算法

赵弘杨, 王靖亚

(中国人民公安大学信息技术与网络安全与学院，北京 100038)

城市路网的快速建设和汽车迅速普及，给人民群众的生活带来极大便利。同时，也使流窜犯罪作案的态势高发。犯罪嫌疑人在作案后往往会选择驾车逃离，由于机动车行驶速度高并且机动性强，给公安机关的追捕工作带来了较大的挑战。

在公安基层办案过程中, 视频侦查技术有着快捷与高效的战术地位, 为锁定、抓捕嫌疑人提供有利条件。对于逃逸车辆抓捕，在实战中是通过对监控视频的回看，发现车辆运行轨迹，进而进行警力部署。但这种方法往往受到诸多因素的影响，比如在视频覆盖率较低的地区，逃逸车辆可能会绕开监控设备；或者因为监控摄像头出现故障、天气影响等因素导致目标车辆难以识别等，一旦追踪目标丢失，追捕问题就会陷入僵局。因此仅通过视频侦查难以实现对目标车辆的追捕。

对于逃逸车辆围堵问题，文献[1]提出了两种模型：针对事件影响较大的最优布控圈模型和针对警力不足地区的关键路径布控模型，但这两种模型的假设条件过于理想化，道路复杂程度与实际情况相比过低，而且没有给出具体的模型求解算法。

文献[2] 建立了以犯罪嫌疑人在逃时间最短，最少警力消耗为基本准则的0～1整数规划模型，基于最近优先的贪心策略，设计基于围堵闭集的快速围堵算法，并且对于生成的围堵圈可以作动态调整，进而得到最佳围堵方案，但快速围堵算法的整体时间复杂度过高，且最近优先的贪心策略不总能满足最小代价的警力调度。

文献[3-5]都将逃逸车辆追捕问题转化为二维平面点集求凸包的问题。文献[3]使用了Graham扫描算法进行凸包的求取。文献[4]中优化了传统的凸包算法，进一步降低了算法的时间复杂度。文献[5]提出单纯使用凸包并不是最优解，在某些特殊情况下得到的结果会有冗余或者缺漏，不能对目标车辆形成完全围堵，但没有给出具体解决方案。

文献[6]利用图论研究了围堵问题，提出了一种基于Dijkstra的最小闭集生成算法，并加入了一种更新闭集的算法。这两种算法可以保证包围圈区域相对较小，从而得到最优的警力配置方案。但没有利用监控系统可能提供的信息，造成了警力的浪费。

综上所述，通过分析各个方案的优缺点，提出基于凸包理论的目标车辆动态围堵算法，对快速凸包算法进行改进，克服凸包理论应用在围堵问题时的缺陷，形成对于目标车辆的包围圈，并根据时间推移和监控系统提供的信息对包围圈进行动态调整，从而达到“围”的目标。将警力调度问题转化为求加权二分图最小权匹配问题，再对该图匹配问题求解得到最小代价的警力部署，从而达到“堵”的目标。

1 问题描述与分析

1.1 问题描述

假设某市某路口发生重大刑事案件，t0(min)后接到报警电话，犯罪嫌疑人已经驾车逃跑，警方通过查看监控系统可能会得到逃逸车辆的若干时空信息，现需要给出最小代价的警力调度方案。为了最大程度地减少目标车辆在逃逸过程中所造成的危害，形成的警力调度方案应当满足以下3点要求[7]：①目标车辆在逃时间尽可能短；②需要封锁的路口最少，从而警力消耗最少;③警力应先于目标车辆到达需围堵的路口。

1.2 问题分析

围堵问题可以化为为两个子问题：向哪些路口派遣警力；对需要派遣警力的路口，如何调度现有警力。对于第一个问题，先以目标车辆为中心计算求出目标车辆可能逃往的范围，再对逃逸范围内的所有路口集合M使用快速凸包算法求得初步的围堵集合Q,然后针对传统凸包算法存在的缺陷设计算法更新集合Q，此时向Q中的路口派遣警力就能形成对目标车辆的绝对围堵。

目标车辆围堵问题要满足约束条件：警力应先于目标车辆到达需围堵的路口[7]。因此要先对集合Q中的所有路口进行检测，判断是否满足约束条件，对于不满足约束条件的路口从集合Q中剔除，并将与该路口直接相连且不属于M的所有路口加入集合Q，并再次判断，直到Q中所有路口都满足约束条件，并记录满足约束条件的警力点。此时会出现这样的情况：一个围堵路口附近可能有多个警力点，而一个警力点周围也可能有多个围堵路口，而且每个警力点到达指定围堵路口的代价各不相同。因此如何调度警力，使完成围堵任务的代价最小很有研究必要。

对于警力调度问题,文献[2]提出了最近优先的贪心策略思想，即对于集合Q中的路口，选取离该路口最近的警力，但这种策略不总能满足最小代价的警力调度。如图1所示，左侧表示警力点，右侧表示围堵路口，连线上的数值代表警力点到达围堵路口的代价，可视为路程。若按照文献[2]的最近优先策略，得出的调度方案为{(A，1)，(B，2)，(C，3)},调度方案的总代价为13。但调度方案为{(A，2),(B，1),(C，3)}时，总代价为10,这说明最近优先策略不总能实现最小代价警力调度。

警力调度问题可以视为分配问题(assignment problem)，而对于分配问题可以转化为在加权二分图中寻找权重之和最小的匹配。二分图的一个匹配指：给定一个二分图G=(V，E)的子图S，如果S的边集中任意两条边都不依附于同一个点，则称S是一个匹配[8]，如图1中红色的边就为二分图的一个匹配。如果一个二分图的某个匹配中，所有的顶点都是匹配点，那么它就是完美匹配，如图1中红色的边也是完美匹配。

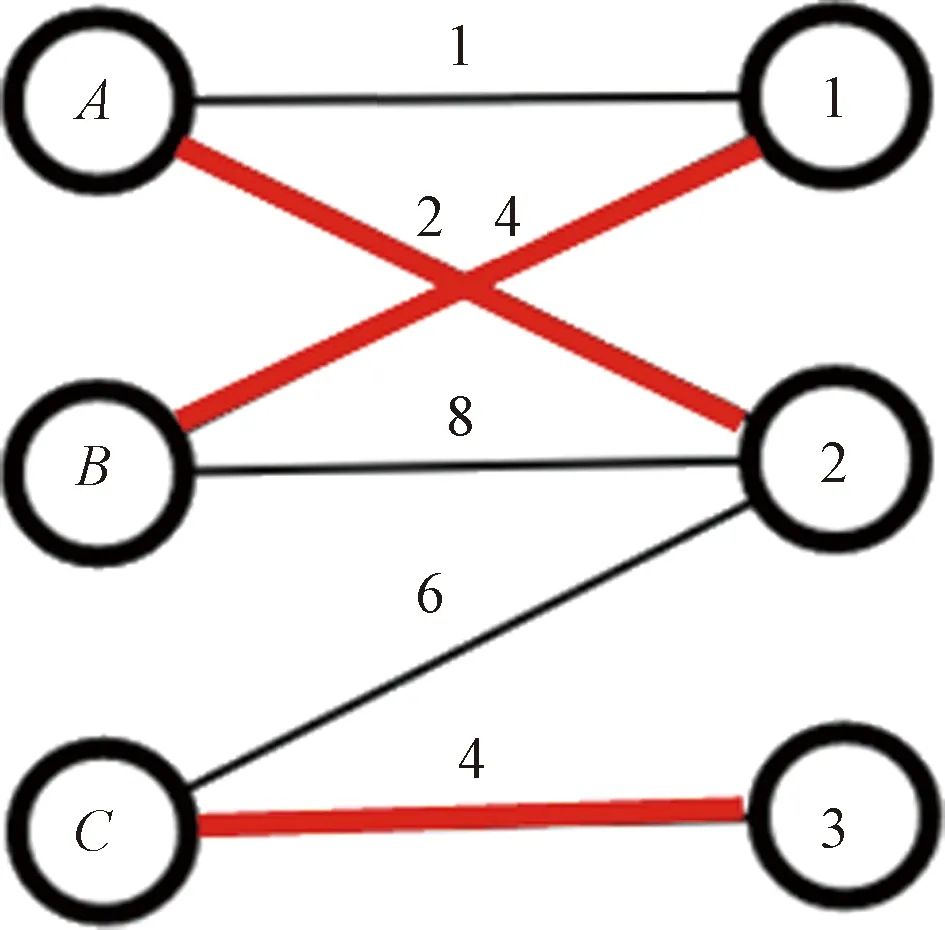
图1 调度示意图

为此，可以将包围圈生成算法求出的围堵集合Q，警力与围堵路口到达关系E，警力集合P，以及路口间权重Wij，共同组成加权二分图G==。并求该加权二分图的最小权完美匹配，所得的解可以视为代价最小的警力调度方案。

而由Kuhn[9]提出、Munkres[10]改进的Kuhn-Munkres(K-M)算法是解决带权二分图匹配问题的一种较为高效的算法，该算法把求最大权匹配问题转化为求二分图的完美匹配，最终得到一个最大权完美匹配。但本文中所求的是二分图的最小权完美匹配，因此只需将权重取负值即可使用K-M算法求得警力调度方案

2 凸包算法研究

2.1 凸包

凸包(convex hull)是计算几何中的概念。定义为：由集合G⊆Rn中点的所有凸组合所组成的集合为P的凸包：

Conv(P)={θ1x1+θ1x2+…+θkxk|x1,x2,…,xk∈

G,θ1+θ2+…+θk=1,θi≥0}

(1)

平面凸包的求解属于计算几何的范畴，在二维欧几里得空间中，凸包可想象为一条刚好包着所有点的橡皮圈，如图2所示。

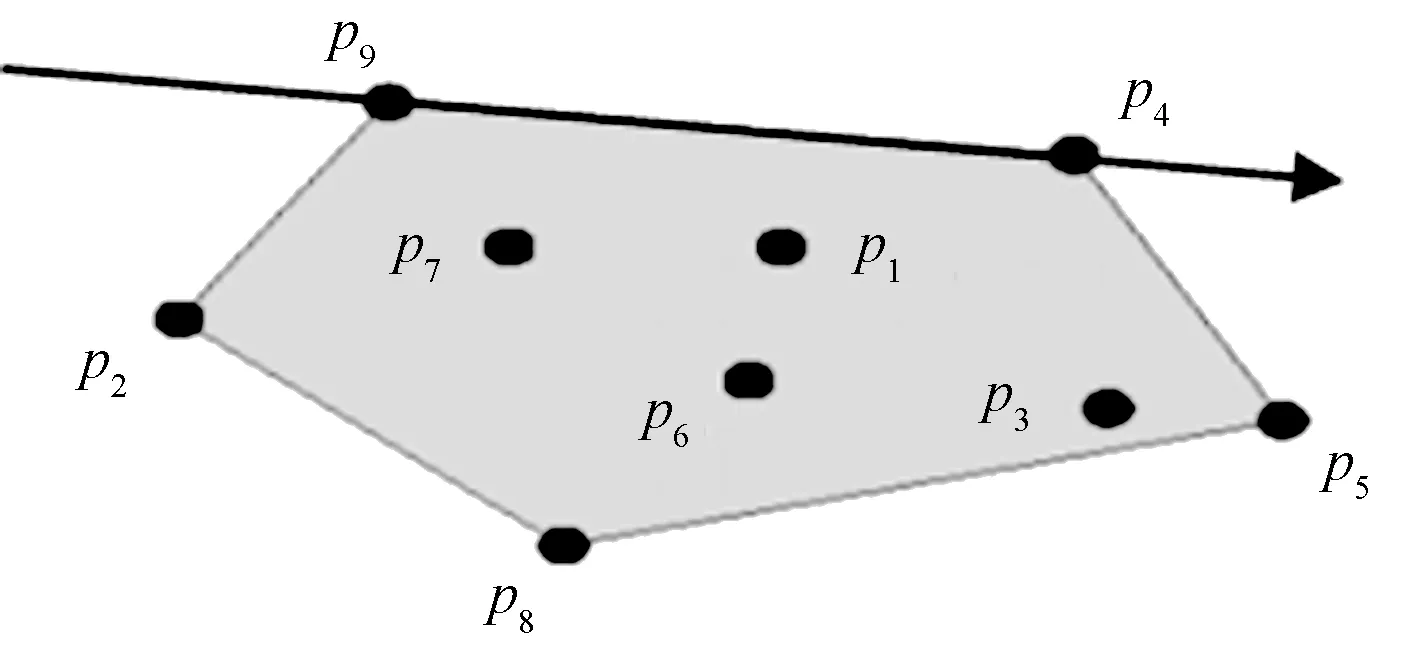
图2 凸包示意图

2.2 凸包算法选型

凸包的常用生成算法有卷包裹算法、Graham扫描法、快速凸包算法等。卷包裹算法的基本思想是：从一个必然在凸包上的点开始向着一个方向依次选择最外侧的点，当回到最初的点时 所选出的点集就是所要求的凸包。卷包裹算法的复杂度是O(NH),N是需求凸包的集合元素数量，H表示最终在凸包上的元素数量，因此卷包裹算法很适合凸包上的点很少的情况，但若凸包上的点增多时，算法的时间复杂度也随之上升，最坏情况下会达到O(N2)。

Graham扫描法的基本思想是：维护一个凸壳，通过不断在凸壳中加入新的点和去除影响凸性的点 最后形成凸包。算法主体由排序和扫描两部分组成，时间复杂度为排序O(Nlog2N)+扫描O(H),整体是一个时间复杂度为O(Nlog2N)的算法。虽然在点集随机时 Graham扫描法不如卷包裹算法，但在最坏情况下，Graham扫描法表现比卷包裹算法好。Graham扫描法也存在一些缺点，如在排序阶段的极角计算会取近似值，这将会导致误差，而且对于共线问题没有给出通用的解决方法。

快速凸包算法的基本思想是关注凸包边界附近的点，逐步丢掉凸包内部的点。快速凸包是一个和快速排序很相似的算法，采用分治的思想，通过向量叉乘将整个凸包集合划分成两个，再分别求出上下凸包，最后合并上下凸包得到凸包，如图3所示。快速凸包算法在点集均匀分布时时间复杂度达到了O(N)，在绝大数情况下平均时间复杂度为O(Nlog2N)。

综上所述，卷包裹算法在点集随机分布时求凸包比较高效，Graham扫描算法适用于点集很密集的情况。而快速凸包算法兼顾了卷包裹算法和Graham扫描算法的优点，适用于对复杂路网的凸包求取。为此，采用快速凸包算法(quick convex hull algorithm)进行凸包求取。

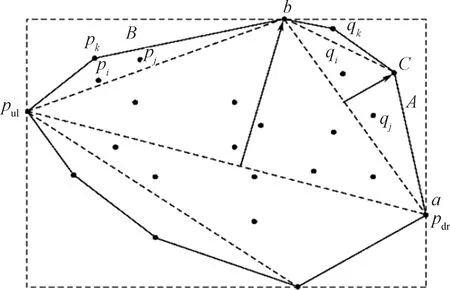
图3 快速凸包算法

2.3 快速凸包算法在围堵问题中的缺陷

在实际情况中，如果单纯使用快速凸包算法来解决围堵问题会出现一些问题。如图4是某市真实路网图，其中蓝色虚线形成的多边形表示单纯使用凸包算法形成的围堵区域，多边形上的红色的点表示需要派遣警力的路口。但A点路口是一个冗余路口，不必派遣警力前往该路口，而B点路口没有纳入围堵集合，逃逸车辆可以通过该路口突破包围圈。

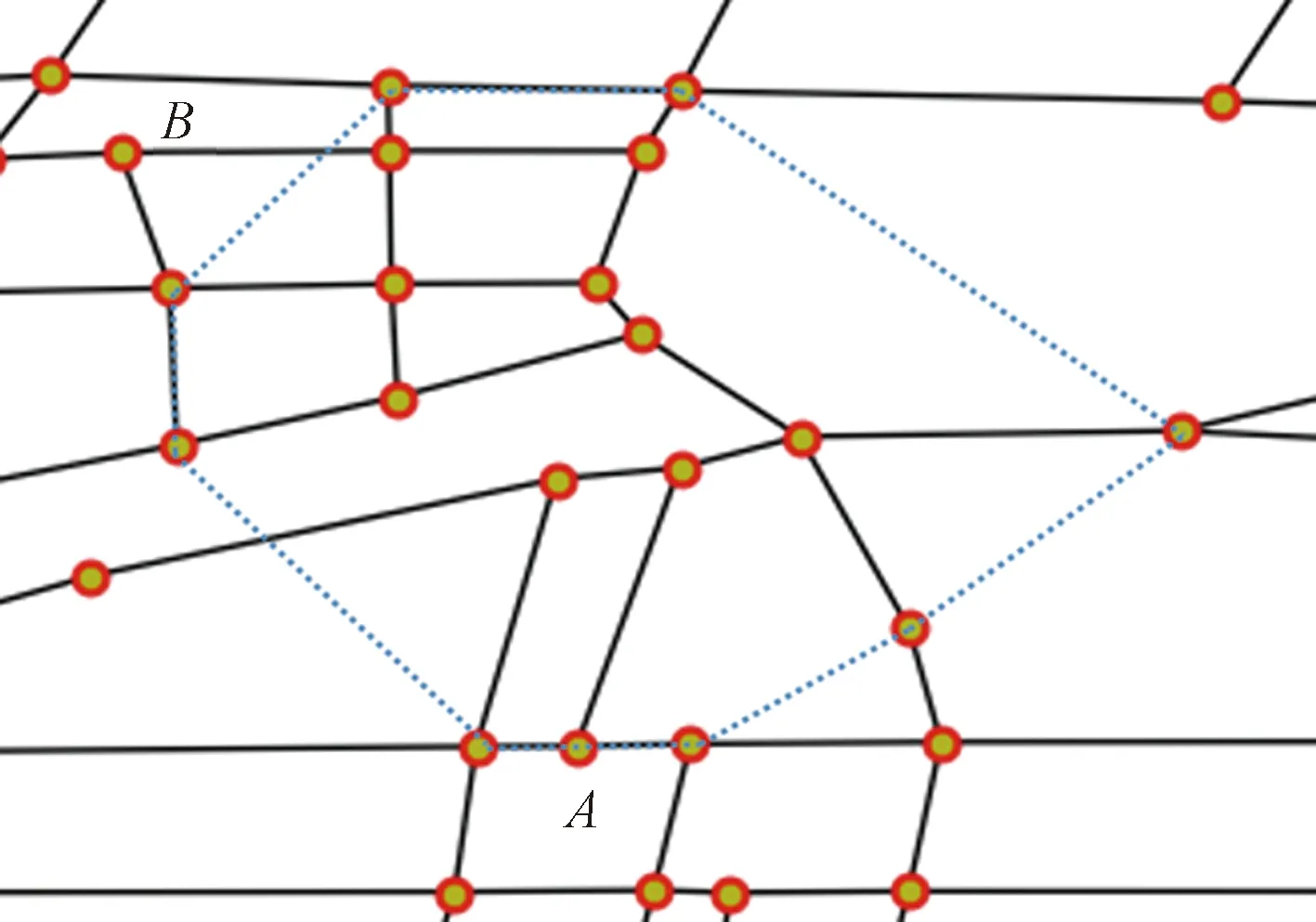
图4 有缺陷的围堵集合

凸包计算运用元素间的位置关系排序后进而求出凸包，不关心元素间的连接关系。而现实路网中，路口之间的连通关系对于逃逸车辆围堵问题来说是至关重要的，因此单纯将凸包算法应用到目标车辆围堵问题上是不合适的，在某些情况下，甚至一些凹型节点可能更合理。

虽然使用凸包理论解决围堵问题会存在缺陷，但凸包算法凭借其优异的算法效率可以快速计算出围堵集合的主体部分，再通过设计更新算法弥补缺陷，从而在较短时间内求出围堵集合。

3 基于快速凸包算法的动态围堵方案

3.1 动态围堵基本思想

基于凸包的动态围堵方案分为两个步骤，第一步骤求取围堵集合Q，第二步骤给出警力调度方案。对于第一步骤，使用基于凸包理论的最小包围圈生成算法求取围堵集合Q，该算法基于快速凸包算法，对传统凸包算法存在的缺陷进行改进后生成围堵集合Q，并随时间推移或者目标车辆位置信息更新而动态调整围堵集合Q；对于第二步骤，使用基于图匹配理论的警力调度算法给出警力调度方案，该算法首先判断围堵集合Q是否满足约束条件，不满足对集合Q进行更新，满足约束条件后，根据已有信息生成二分图，并利用K-M图匹配算法求出二分图的最小权完美匹配，从而得到最小代价的警力调度方案。算法整体流程图如图5所示。

图5 算法流程图

3.2 形式化定义

围堵问题的相关概念形式化定义如下：设G=是一个加权无向图，表示路网信息，其中：

(1)V={v1,v2,…,vn},表示该区域的所有路口节点，n表示路口节点的数量。

(2)x∈V,表示目标车辆在监控系统最后一次出现的路口，若监控系统没有捕到目标车辆，x为案发地点。

(3)tnow为当前时间，且不断增加；tx表示目标车辆在监控系统最后一次出现的时间，若监控系统没有捕捉到目标车辆，则tx为案发时间。

(4)Δt=tnow-tx,表示当前时间与目标车辆在监控系统最后一次出现时间的差值，若监控系统没有捕捉到目标车辆，则Δt为当前时间与案发时间的差值。

(5)wij=dis(vi,vj),表示任意两个路口vi,vj之间最短路径上的距离。

(6)P={p1,p2,…pl},pi∈V,表示该区域的警力点,l表示警力点的数量，并假设警力点刚好在路口上。

(7)Q={q1,q2,…qk},qi∈V,表示包围圈集合，k表示包围圈集合的数量，即需要派遣警力的路口。

(8)tij=wij/vp,表示号警力到达vj号路口所需要的时间，vp表示警力的移动速度。

(9)txj=wxj/vc,表示目标车辆从x路口到vj号路口的时间，vc表示目标车辆的移动速度。

(10)M={m1,m2,…,mx},mi∈V,表示以路口x为圆心vcΔt为半径的圆内所有的路口节点。

(11)E={(qi,pj)|qi∈Q,pj∈P},表示在满足约束条件的情况下，可以到达围堵路口qi的警力点pj。

(12)警力调度E*={(qi,pj)|qi∈Q,pj∈P},表示向围堵路口qi派遣警力点pj。

(13)NLi表示与节点vi相邻的所有节点的集合[11]。

3.3 最小包围圈生成算法

最小包围圈生成算法旨在以目标车辆为中心，基于快速凸包算法形成一个数量最少的围堵路口集合，并随时间推移以及目标车辆的位置更新对围堵集合进行动态调整。

最小包围圈生成算法步骤如下：

Step 1： 输入目标车辆最后一次出现的地点x，在逃时间Δt=tnow-tx；

Step 2： 根据位置x，以及Δt求得路口集合M；

Step 3： 对路口集合M使用快速凸包算法求出初始围堵集合Q=Quickhull(M)。

Step 4： 令Temp1=M-Q,Temp2=V(G)-M,当Temp1≠Ø 时，重复如下步骤：

Step 4.1： 任取∀v∈Temp1，并使Temp1=Temp1-{v}。

Step 4.2： 若NLv∪Temp2≠Ø,则Q=Q∪{v}。

Step 5： 当Temp1=Ø时,令Temp3=Q。若Temp3≠Ø时，重复如下步骤：

Step 5.1： 任取v∈Temp3，Temp3=Temp3-{v}。

Step 5.2： 若NLv∪Temp2=Ø,则令Q=Q-{v}。

Step 6： 当Temp3=Ø时，Q为初步求得的需要派遣警力的路口集合，输出Q；

首先根据位置x以及Δt得到目标车辆可能位于的路口集合M，再通过快速凸包算法求出给定集合M的凸包Q。由于凸包计算只关心点集的位置关心，不关心点间的连接关系。而对路口间的连接关系进行分析对于围堵问题来说是必须的，因此单纯使用凸包算法求出的凸包集合Q不能满足围堵集合的要求，可能会出现路口节点的冗余和缺漏。为解决这两个问题，Step 3完成了对围堵集合的补漏，保证了包围圈的绝对围堵。Step 3通过判断Q集合中的点是否与包围圈以外的点有连接关系来确定哪些点是冗余点，随后将这些点从Q集合中剔除，从而得到最小围堵集合Q。每隔30 s，或者目标车辆在监控系统中再次出现(表明位置x，以及Δt=tnow-tx都发生改变)，则转到步骤1，根据新的位置x以及Δt对包围圈进行更新。

3.4 警力调度算法

警力调度算法旨在根据警力分布情况，判断围堵集合Q是否满足基本原则：警力应先于目标车辆到达需围堵的路口，并对不满足约束条件的围堵集合Q进行更新。最后使用K-M算法求出警力调度方案。

在给出警力调度算法之前，定义警力到达围堵路口所需的时间矩阵T:

对于警力时间矩阵T中的任意元素tij,表示pi号警力到围堵集合中qj号路口所需的时间。向量tx={tx1,tx2,…,txk},对于任意的txj表示逃逸车辆从案发地x到qj号围堵集合路口所需时间。其中k为围堵集合中路口的数量，l表示该区域警力数量。并构造逃逸车辆时间矩阵Tx：

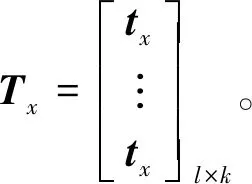
最小包围圈生成算法步骤如下：

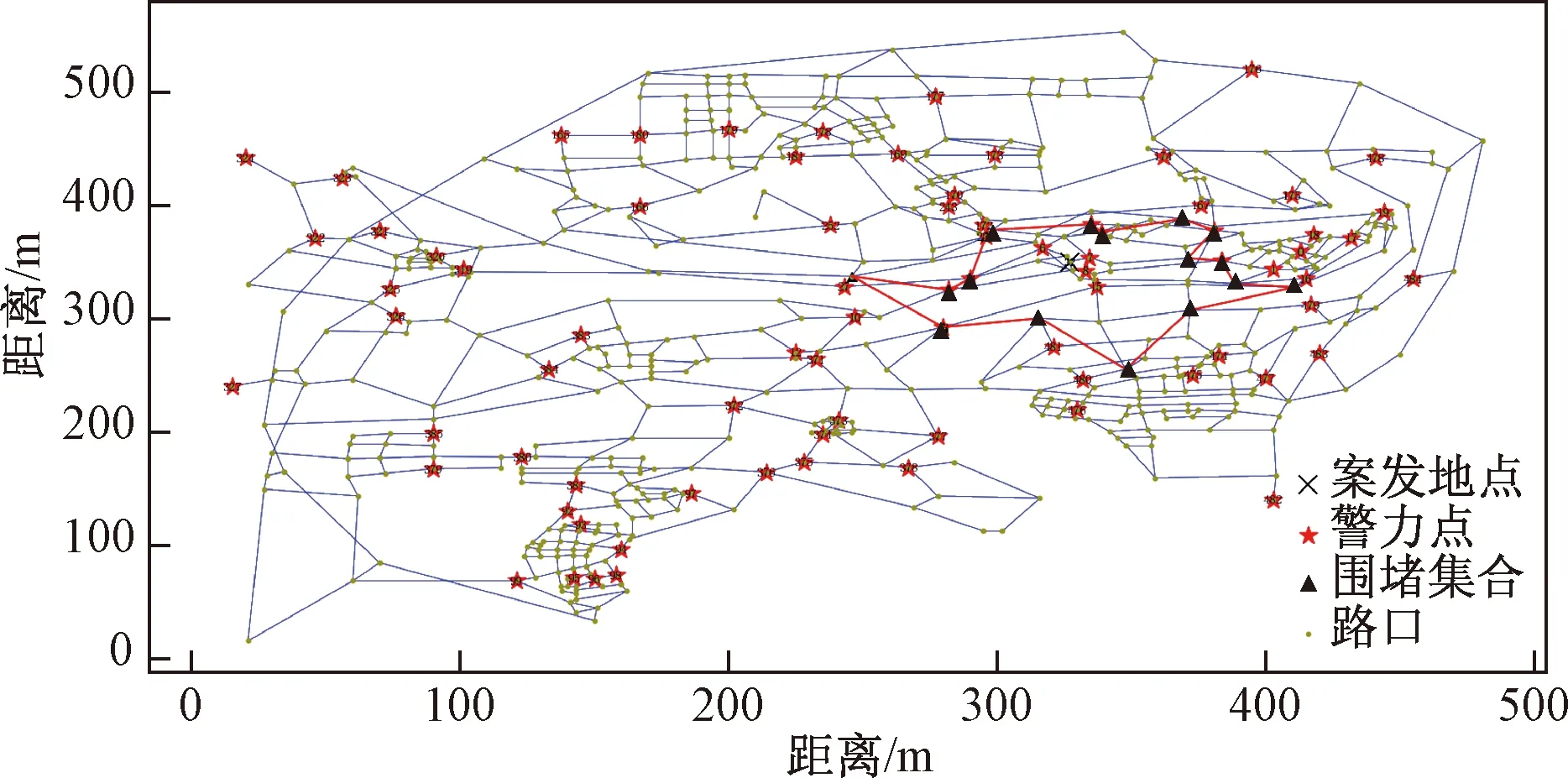
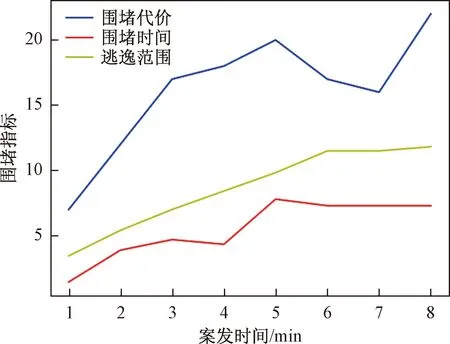
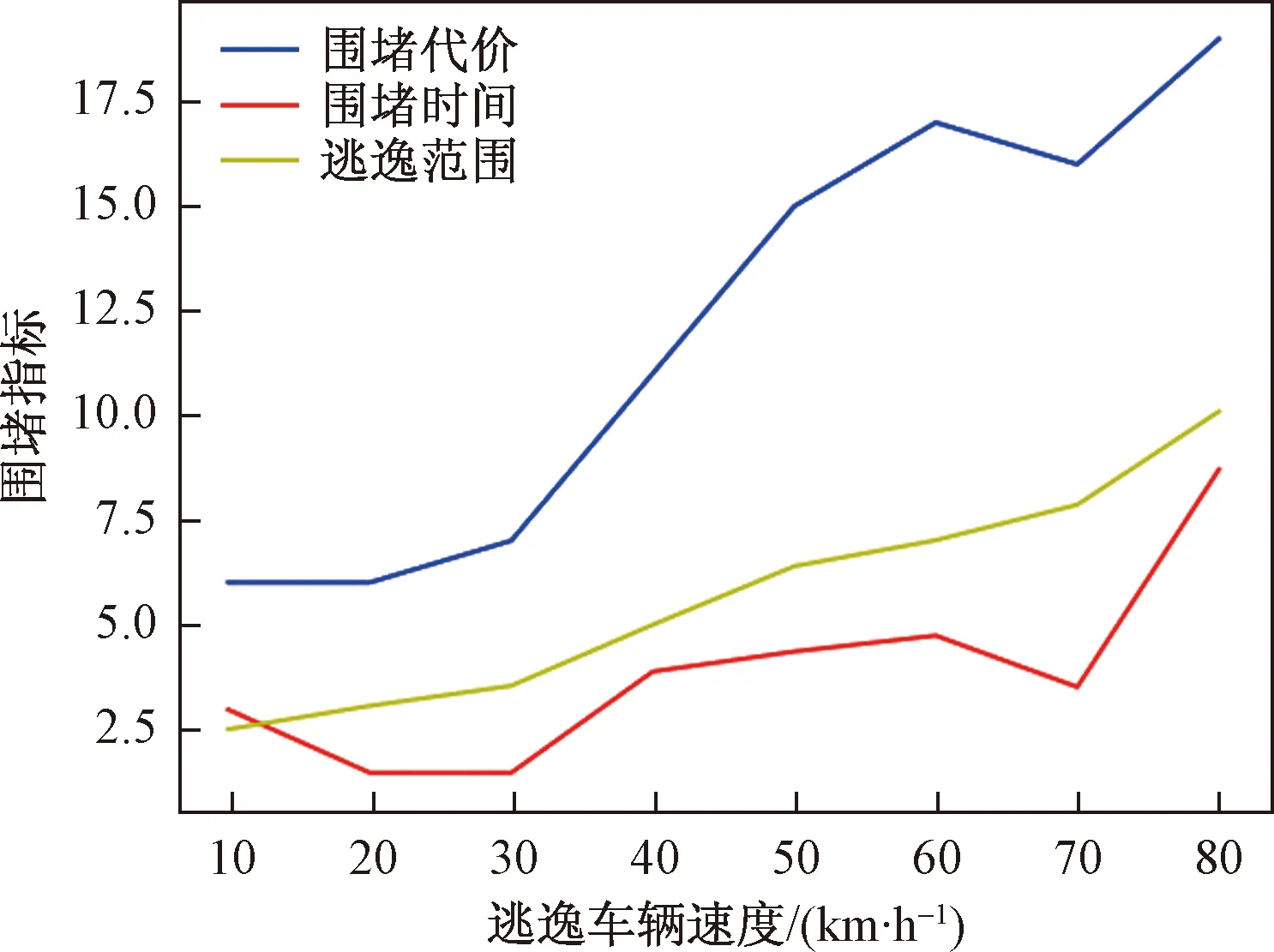
Step 1： 根据围堵集合Q，构造警力时间矩阵T和逃逸车辆时间矩阵Tx。令flag=1；若l

Step 2： 令ΔT=T-Tx=[ΔT1,…,ΔTk]，其中ΔTi=[t1i-tx,…,tli-tx]T,P*={}(空集)；

Step 2.1： 遍历矩阵ΔT，对于每一个ΔTi：

若ΔTi中的元素都为正值，则令Q=Q-{vi}，Q=Q∪[NLvi-(NLvi∩M)]，flag=0；

若ΔTi中的元素有负值，则令这些负值的索引值为index，并使E∪(vi,vindex),P*=P*∪pi；

Step 2.2： 若flag= =0，执行Step 1，否则执行Step 4。

Step 3： 警力不足，围堵失败。

Step 4： 根据围堵集合Q、警力集合P*、到达关系E，组成二分图G=(Q，E,P*)。

Step 5： 求得警力调度方案E*=K-M(G)。

最小包围圈生成算法给出了经去重补漏的围堵集合Q，但集合Q只是在几何层面上达到了绝对围堵，没有考虑实际约束条件tij≤txj，即警力到达围堵集合Q所用的时间应当小于等于目标车辆到达该路口的时间。

Step 1首先判断警力数量是否小于围堵集合Q中的元素数量k，若l

3.5 动态围堵算法分析

基于凸包的动态围堵算法主要包括两个子算法，分别为：基于快速凸包算法的最小包围圈生成算法、基于K-M匹配算法的警力调度算法。由于这两种子算法在每一步都给出了最优解从而保证了整个算法能够得到全局最优解。

时间复杂度作为衡量算法性能的标准之一是值得分析的，令T(n)sum表示算法整体的时间复杂度，T(n)E、T(n)D分别表示最小包围圈生成算法和警力调度算法的时间复杂度。其中T(n)E=O(nlog2n)，n为集合M的元素数量|M|;T(n)D=O(n3),n为围堵路口数量k加上满足约束条件的警力点数量|P*|。由于这两种子算法相对独立，因此T(n)sum可表示为

T(n)sum=T(n)E+T(n)D=

O(nlog2n)+O(n3)=O(n3)

(1)

结果表明，本文中提出的基于凸包的动态围堵算法是一种多项式时间算法，能够在相对较短的时间内给代价最小的警力调度方案。

4 实验结果分析

4.1 实验结果

为了验证算法的可实用性，以2011年全国大学生数学建模竞赛B题数据为例[12]，假设逃逸车辆的速度与警车的速度都为60 km/h, 案发地点如图6所示为32号路口，案发3 min后接到报警。

图6 围堵示意图

由Python编程实现上述算法,得到的围堵集合如图6所示，黑色三角代表围堵路口，五角星代表警力点，红色实线所围成的区域就是逃逸车辆位于的区域，由于算法对围堵路口集合进行了更新调整因此最终的围堵边界并不是凸边型；得到警力到达关系见表1，其中得到警力调度方案见表2,其中围堵路口序号代表围堵集合Q，警力位置序号代表警力点集合P。

表1中，第一列表示围堵集合中的元素，第二列表示可以满足约束条件到达围堵路口的警力点集合，通过该表发现，某些围堵路口可选的警力点只有一个，某些围堵路口可选警力却有很多，这说明该市的警力分布不是很合理。

表1 到达关系

表2表示的是案发3 min接到报警后算法给出的围堵方案。其中实际耗时间为0时，表明警力点刚好位于为围堵路口上。此时，围堵路口的个数为17个，平均围堵时间为1.35 min，最大耗时的路口是59号路口，需要4.74 min，因此对目标车辆形成完全围堵最少需要4.74 min。

表2 警力调度方案

4.2 数据分析

对于目标车辆围堵问题，围堵时间、围堵代价、逃逸范围都是值得关注的围堵性能。

(1)围堵时间指的是从接到报警开始到警力点到达各自的围堵路口结束所用的时间，在数值上等于耗时最大的警力所花费的时间T:

T=max{wij/vp},∀i∈Q,∀j∈P

(3)

(2)围堵代价指的是需要派出警力的数量，也就是围堵集合的元素数量k=len(Q)。

(3)逃逸范围指的是逃逸车辆从案发位置到围堵集合Q的平均距离S:

(4)

因此通过对实验数据进行分析，探究了案发时间t0、逃逸车辆速度vc对上述围堵性能的影响。

如图7所示，设案发地点为x=32,vc=60 km/h，vp=60 km/h,以t0=1 min起，到t0=8 min结束，三条折线分别表示三种围堵性能。可以发现以该市的路网拓扑和警力分布：围堵代价随案发时间的增加而增大；围堵时间先上升，当t0=5 min时达到最大，随后平稳。逃逸范围随案发时间的增加而增大在t0=6 min时达到最大，随后趋于平稳。

图7 案发时间对围堵性能的影响

图8 车辆速度对围堵性能的影响

如图8所示，在t0=3 min，其他条件不变的情况下，以逃逸车辆速度vc=10 km/h起，到vc=80 km/h结束。可以发现随着逃逸车辆速度的增加三种围堵指标都随之不断增大。

综上所述，在该市的路网拓扑和警力分布的情况下，围堵代价会随着案发时间的增长和逃逸车辆速度的增大而逐步上升。围堵时间会随着案发时间的增大而增加，随后趋于平稳；随着逃逸车辆速度的增大而减少。围堵质量随着案发时间的增加而降低，但与目标车辆速度关联性不大。

5 结论

为了以最小代价快速抓捕逃逸的目标车辆，提出了基于快速凸包算法的最小包围圈生成算法，针对凸包算法中存在的缺陷进行改进，得到了最小代价包围圈，并利用逃逸车辆的时空信息以及路网拓扑特定对包围圈进行动态调整。将警力调度问题转化为二分图最小权完美匹配问题，并给出了基于K-M匹配算法的警力调度算法，求得最小代价警力调度方案。通过对实验数据的分析，可知随着案发时间增大，所需投入的警力资源增大到一定程度后会趋于平稳，而随着逃逸车辆速度的增大，警力资源的消耗会一直增大。

本文中给出的算法简洁、实用，在已知路网拓扑图、警力分布情况以及目标车辆最近一次出现的位置后就能够在相对较短的时间内获得全局最优解。为快速围堵目标车辆提供了一种有效的方法，具有较大的实际意义和应用价值。