一种全局隶属度和小波能量相结合的活动轮廓模型

胡 瑄, 汪兆栋

(景德镇学院机械电子工程学院，景德镇 333000)

肺癌一直是导致人类死亡的危险疾病之一[1]。磨玻璃型(ground glass opacity, GGO)肺结节(pulmonary nodules, PN)是肺癌的初期症状之一，而越早被确诊为肺癌的患者的治愈率也越高。因此，研究计算机辅助检测磨玻璃型肺结节对人类生命有着重要意义。

GGO结节可分为两类[2]：①部分实质磨玻璃型结节(part solid ground glass opacity pulmonary nodules, PSGGOPN)，具有模糊边界和亮度不均匀性; ②实质型磨玻璃肺结节(solid ground glass opacity pulmonary nodules,SGGOPN)，其背景亮度高度相似。由于模糊边界，GGO肺结节的低对比度和强度不均匀性，GGO结节的准确分割仍然是一个极其困难的问题。为了精确地分割GGO结节，已经开发了许多算法，例如采用增强K-最近邻(K-NN)的非参数方法[3]。由于使用纹理似然图，该方法可以应对GGO结节的低对比度。然而，非参数密度函数难以描述亮度不均匀的物体，因此K-NN的非参数方法不能准确地分割具有强度不均匀性的GGO结节。

活动轮廓模型(active contour model,ACM)因其精度高、易于实现、且能提供平滑、闭合的轮廓曲线，已广泛应用于目标区域提取中。一般来说，ACM可分为3大类[4]：基于边缘的ACM[5]、基于区域的ACM[6]和混合ACM[7]。基于边缘的ACM利用图像梯度来识别物体边界，这些模型不仅对噪声非常敏感，而且难以区分弱边界与强纹理；而且，最终的结果高度依托于预设曲线的精度。基于局部空间的ACM不仅利用了预测曲线附近的图像特征，而且利用轮廓内外区域的概率分布。与基于边缘的ACM相比，该方法能区分出弱边界与强纹理，且对噪声鲁棒，但该方法基于亮度均匀假设，该假设限制了该方法的应用范围。混合ACM将基于边缘的ACM引入到基于局部区域的ACM中，该模型结合了基于边缘的ACM和基于区域的ACM的优点，然而，混合ACM仍然不能准确地分割GGOPN。

为精准分割GGOPN，文献[8]提出基于局部区域信息的活动轮廓模型(local region active contour model,LRACM)。由于使用局部区域信息，LRACM可以应对场景中的模糊边界和亮度不均匀性问题。然而这类模型不能精确地分割低对比度的物体。文献[9]提出基于小波变换的分割方法。小波系数可以增强对象与其背景之间的差异，因而可用于解决低对比度问题。在此基础上，文献[10-11]提出了一些改进的方法。然而，基于小波变换的分割方法忽略局部区域信息，因此不能准确地分割具有亮度不均匀性的物体。

针对上述缺陷，提出基于全局隶属度和小波能量相结合的活动轮廓模型(global membership combined with wavelet energy for active contour model, GMWEACM)，该模型利用全局隶属度函数调整初始活动轮廓曲线，使之与待分割目标更贴近；同时，基于全局隶属度的边界停止函数值在目标边界处将快速减小为0，以避免了预测曲线远离目标边界；其次，基于小波能量的ACM数据项增强了前景与背景之间的对比度，以解决传统算法在亮度值相似或光照不一致的场景中的误分割问题。

1 应用全局隶属度函数构造边界停止函数及初始轮廓曲线

为使活动轮廓曲线收敛于目标轮廓边界，提出基于全局隶属度函数的边界停止函数，该边界停止函数值在目标边界处为0。计算过程如下：

计算待分割区域内所有像素点的属于前景或者背景的概率u1(x)及u2(x)。其中：u1(x)为属于前景的概率；u2(x)为属于背景的概率。

进而应用u1(x)及u2(x)重构边界停止函数:

S(x)=ε{1-e-[(u1(x)-u2(x)]}

(1)

式(1)中：ε是一个常数。

根据模糊聚类理论易知，边界处无论是模糊的还是清晰的，其像素点的u1(x)和u2(x)值相差很小且近似等于0.5(边界点上，属于前景的概率和属于背景的概率近乎相等), 则此时S(x)为0，而越远离边界处的像素点的隶属度特征也越明显，即|u1(x)-u2(x)|越大，S(x)也越大。图1显示了边界停止函数的曲线，可以发现在边界处其值为0，而越远离边界处，其值越大。

传统LRACM模型要求预设的轮廓曲线贴近待分割目标轮廓，不合适的初始活动曲线最终会导致肺结节区域提取的失败。为解决该问题，采用u1(x)及u2(x)调整初始活动曲线的位置及生长方向。调整方法如下：

(2)

式(2)中：ω1表示GGO肺结节类；ω2表示背景类。

求出每个初始活动曲线上的像素点的全局隶属度，若该像素点的前景隶属度大于其背景隶属度，则把该点归于肺结节类，反之亦然。

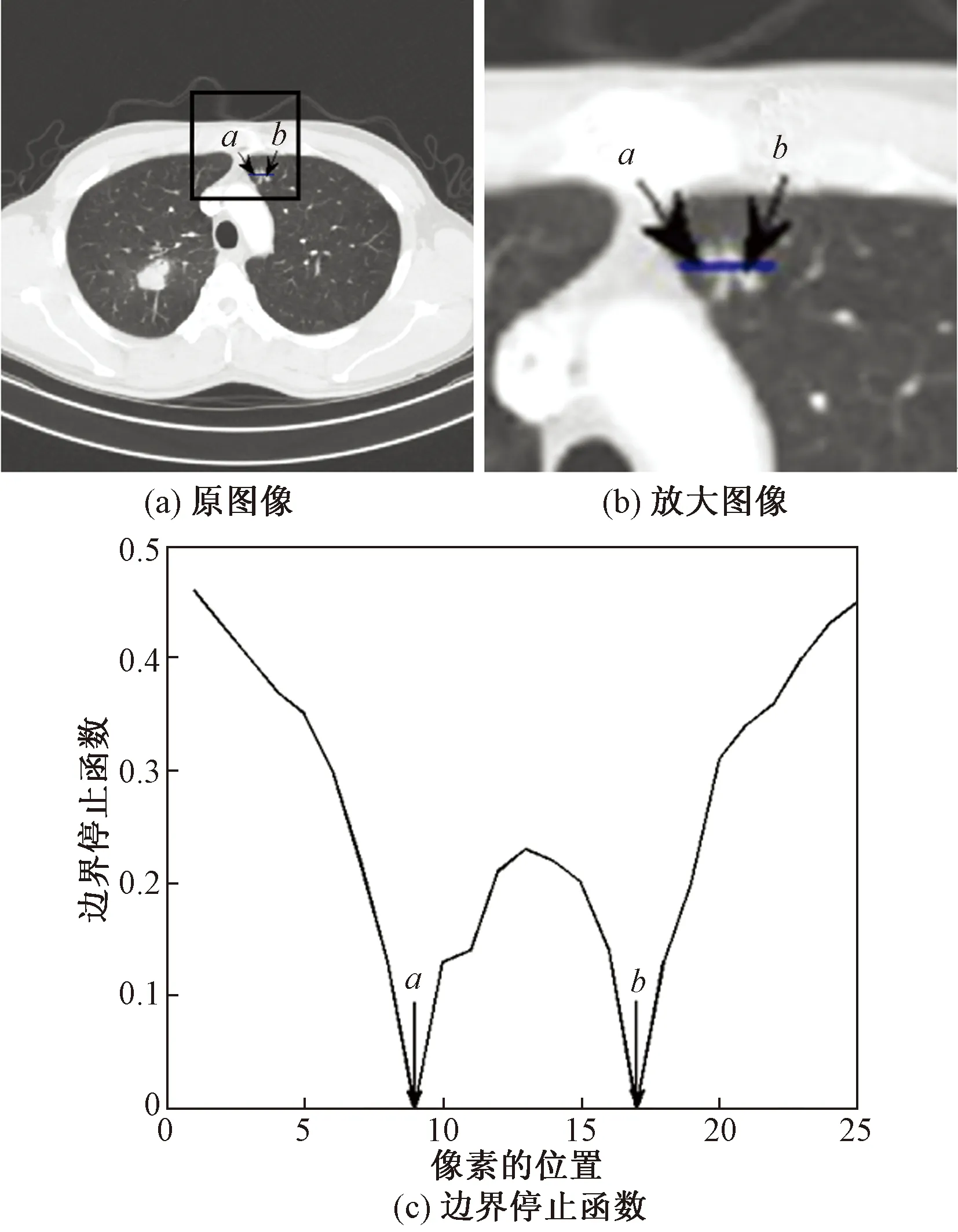
图1 边界停止函数曲线

2 基于小波能量的ACM数据项

LRACM模型中，基于梯度函数的数据项不能在亮度值差异小的区域中准确区分前景和背景，因此采用小波能量(wavelet energy, WE)增强前景与背景的差异。

设图像中任意像素点x，则小波能量W(x)为

W(x)=A(x)+EH(x)+EV(x)+ED(x)

(3)

式(3)中：A(x)为像素点x的似然函数；EH(x)、EV(x)、ED(x)分别为小波能量函数的水平成分、垂直成分及对角成分。

(4)

(5)

(6)

(7)

式中：B为以x为中心的局部空间；y为B中的任意像素点；wA(y)为低频小波系数；wH(y)、wV(y)和wD(y)分别对应水平分量、垂直分量及对角分量的高频小波系数；Kσ(x-y)为方差为σ的高斯核函数。

图2所示为亮度分布和小波能量分布。可以发现，亮度分布下，目标与背景混合在一起，而小波能量分布下，目标与背景能被明显区分开。

图2 亮度和小波能量分布

3 基于全局隶属度和小波能量的活动轮廓模型

文献[8]提出一种经典的基于局部区域的ACM(LRACM), 所提算法正是在该模型基础上的改进。

3.1 能量函数构造

假设一条活动轮廓曲线将图像中局部区域分割成前景区域和背景区域，前景区域定义为Ω1类，背景区域定义为Ω2类，则LRACM的能量函数为

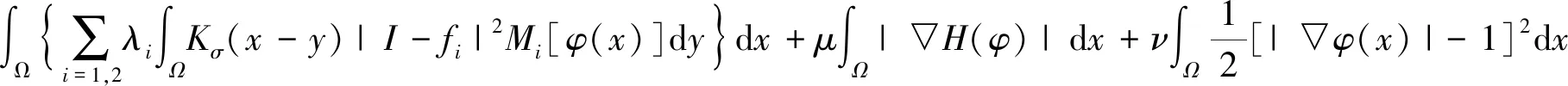
(8)

式(8)中：φ为水平集；μ、λi和ν为常数；I为目标点亮度函数；x代表目标点；y代表目标点邻域点。

(9)

Mi(φ(y))定义为：

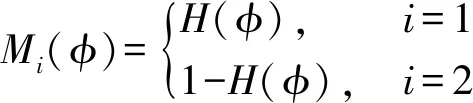
(10)

式(10)中：H(φ)是Heaviside函数[12]。

f1和f2为局部区域内曲线里侧和外侧的亮度均值:

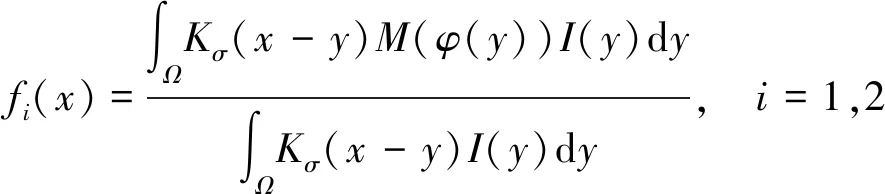
(11)

利用第2节、第3节介绍的方法，将LRACM能量函数改写为

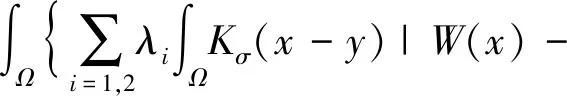
(12)

式(12)中：f1(y)和f2(y)分别为局部区域内活动轮廓曲线里侧和外侧的小波能量均值；W(x)代表小波能量函数；S[|▽H(φ)|]代表边界停止函数；其他参数的意义与式(8)中的相同。

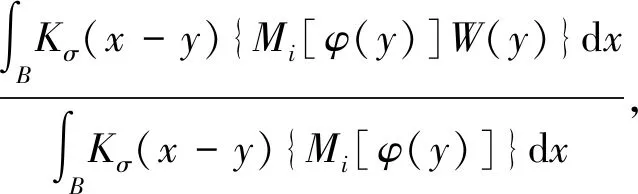
i=1,2

(13)

3.2 能量函数最小化

为演化活动曲线，采用欧拉-拉格朗日方程进行能量函数E(φ)最小化，且计算过程中，保持fi(y)及φ不变。

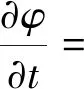
(14)

式(14)中：δ(φ)是Diracdelta函数；e(x)定义为

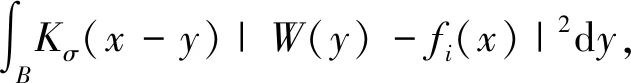
i=1,2

(15)

4 实验分析

为验证算法能精准分割PSGGOPN和SGGOPN，将本文提出的模型及LRACM应用于美国肺影像数据库[13]中，图示其肺结节区域提取结果，并计算其平均性能参数，包括TP(true positive ratio)、FP(false positive ratio)、SD(similarity degree)及平均Tanimono/Jaccard误差率，以验证其算法性能。

图3显示了包含PSGGOPN的CT图像中的肺结节提取结果，其中图3(a)、图3(c)、图3(e)分别对应专家手动分割肺结节区域的示意图，LRACM的肺结节区域提取示意图及本文所提方法的肺结节区域提取示意图，图3(b)、图3(a)、图3(f)分别对应其放大图像。从图中可以发现，LRACM仅分割出GGOPN中的实质部分区域，而把部分颜色较浅的GGOPN区域误判成为了背景，从而导致目标轮廓的缺失，而本文算法的活动轮廓曲线与目标边界线基本吻合。

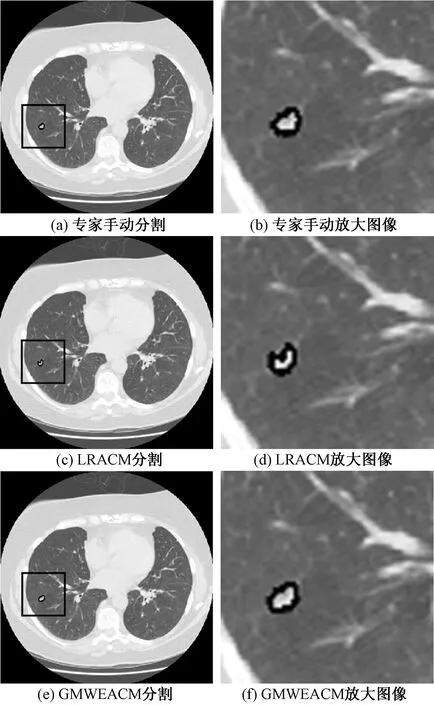
图3 部分实质GGOPN的实验结果示意图

图4显示了包含SGGOPN的CT图像的实验结果，其中图4(a)、图4(c)、图4(e)分别对应专家手动分割的肺结节轮廓示意图，采用LRACM算法的肺结节区域提取及本文所提方法的肺结节区域提取，图4(b)、图4(d)、图4(f)分别对应其放大效果图。从图中可以发现，LRACM把近邻边界处属于肺结节的区域误判为背景区域，同时，由于受边界模糊的影响，活动轮廓曲线产生了边界泄漏，从而导致活动轮廓曲线不平滑、不完整。这是因为基于梯度的边界停止函数在交界处不会停止造成的。而GMWEACM能得到平滑的、完整的活动曲线，且该曲线的形状及大小与专家手动分割的肺结节轮廓基本相同。

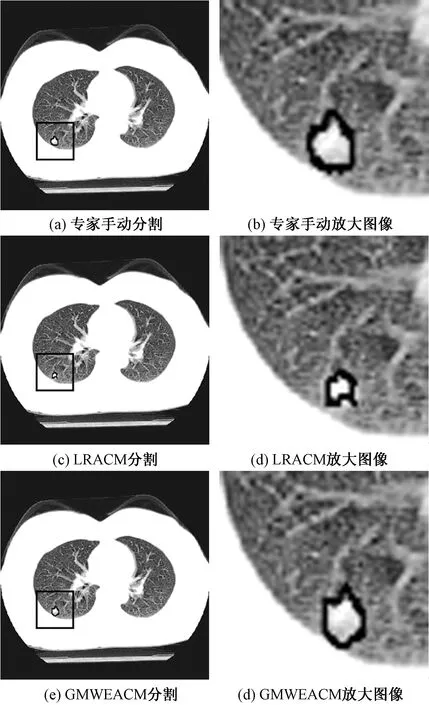
图4 实质GGO肺结节的分割结果

表1、表2记录了本文算法及LRACM在美国肺影像数据库的100副部分实质(part solid, PS)GGOPN图像及100副SGGOPN图像中的平均重叠指数及平均Tanimono/Jaccard错误率。TP为正确分类像素点所占比率；FP为错误分类像素点所占比率；SD为相似度。LRACM的活动轮廓曲线与专家手动分割的目标轮廓总是存在一些偏差，故TP和SD较低，而FP、TJ较高。而GMWEACM所得活动轮廓曲线与专家手动分割的目标轮廓较吻合，所得参数均优于LRACM。再次证明了本文算法优于LRACM。

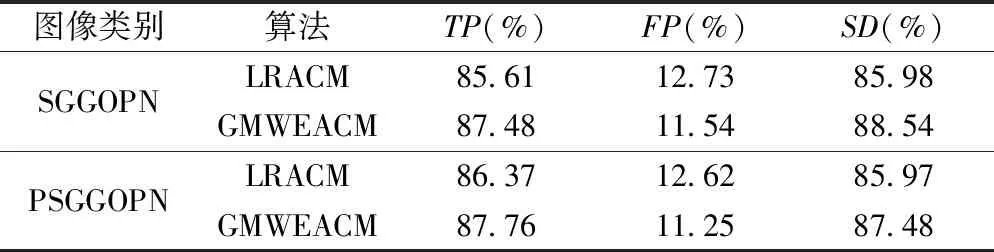
表1 临床GGOPN的平均重叠指数

注：TP为正确分类像素点所占比率；FP为错误分类像素点所占比率；SD为相似度。

表2 临床GGOPN的Tanimono/Jaccard错误率

5 结论

针对CT图像中GGOPN的精确分割问题，提出一种联合全局隶属度和小波能量的ACM。该模型应用全局隶属度函数解决传统ACM要求初始活动轮廓曲线贴合待分割目标的问题，同时全局隶属度函数还被用于构造边界停止函数以解决模糊边界下的难收敛问题；进而，该模型应用小波能量函数解决亮度值差异小的场景下的目标分割问题；最后，将该模型应用于全实质及部分实质GGOPN的CT图像中，实验结果表明，本文ACM能精准地分割非实质及部分实质的磨玻璃型肺结节。