面向稀疏数据集的聚类算法
2020-04-22赵玉明舒红平魏培阳
赵玉明, 舒红平, 魏培阳, 刘 魁
(成都信息工程大学软件工程学院;成都信息工程大学软件自动生成与智能服务四川省重点实验室,成都 610225)
作为知识库发现的一个步骤,数据挖掘可以帮助人们从大型数据库中提取模式、关联、变化、异常及有意义的结构[1]。其中,聚类是数据挖掘的重要研究方向,可以将数据对象分成簇或类,让同一个簇中的对象具有很高的相似性,而不同簇的对象相异。聚类主要源于很多学科领域,包括:数学、计算机科学、统计学、生物学和经济学等[2]。在不同的领域中,都有适用于该领域的聚类技术,并被用来衡量数据之间的相似性,从而对该领域的样本进行有效的划分。
聚类算法可以分为划分聚类、层次聚类以及密度聚类等。它们的共性就是采用欧式距离来衡量类之间的距离,如最近距离单连接(single-link)、最远距离全连接(complete-link)、平均距离聚类(group-average)和中心距离聚类(centroid-similarity)。同时,聚类的基本的框架是搜索和合并,所以每次都要扫描整体数据,进行大量的欧式距离计算。而在此过程中会遇到如下的3个问题:
(1)在数据分布相对离散的时候,数据集中存在大量的空值,如果仍用欧氏距离,反复扫描整个数据集,则会进行大量无意义的计算。导致聚类的时间效率受到很大的影响,如果数据量很大,会导致内存不足的问题。
(2)在数据分布相对离散的时候,使用欧式距离,无法很好的衡量出不同簇之间数据的依赖性以及分布密度不均衡的特点。同时缺乏从数据的整体分布进行聚类,导致聚类的质量产生严重的影响。
(3)在数据分布相对离散的时候,使用欧式距离,计算不同簇之间的距离。更多考虑共同项之间的距离,忽略非共同项之间可能蕴藏的信息。尤其在数据分布呈现极度稀疏性的时候,欧式聚类缺乏考虑数据上下文之间的关系,无法达到预计的聚类效果。
在信息论中,KL(Kullback-Leibler)散度用来衡量用一个分布来拟合另一个分布时候产生的信息损耗。典型情况下,P表示数据的真实分布,Q表示数据的理论分布、模型分布或P的近似分布。当两个随机分布相同时,它们的相对熵为零,当两个随机分布的差别增大时,它们的相对熵也会增大。KL的值越大,说明两个分布差距越大,KL为零则说明分布近似相同[3]。目前,KL散度主要最为图像、信号、声音信号的处理上,文献[3,5-6]的作者,已将开始将KL散度引入到相似性度量上,并且已经取得很好的效果。在文献[4]中,使用KL散度来计算用户的相似性,进而应用在协同过滤算法中,减少了用户评分稀疏性的问题,提高了推荐的质量和效率。
基于以上分析,在面对稀疏数据集的聚类过程中,提供以下的聚类思路:
(1)通过预聚类,根据整体数据集的分布特点,将不同簇之间的数据进行聚类[7]。解决没有考虑数据整体分布的缺点。
(2)构建整体数据集的概率矩阵,然后计算KL矩阵,根据KL矩阵合并数据。完成对数据集的第一次聚类。在计算KL矩阵的时候,借助预聚类中数据的分布特性,考虑不同数据蕴含的信息[8]。解决没有考虑非共同项之间距离以及数据本身信息的缺点。
(3)在完成第一次聚类后,再次重复以上的步骤,直到最后的距离矩阵[9]无法指导聚类为止。而在此过程中,数据只需要在预聚类过程中读入内存,完成对数据的预聚类。后期的工作是处理概率矩阵和距离矩阵。解决了反复扫描数据,进行大量计算的问题。
1 KL散度的引入及数据特征分析
在介绍相对熵之前,首先了解什么是信息熵[10]。
一个随机变量X的可能取值为X={x1,x2,…,xn},对应的概率为P(X=xi)(i=1,2,3,…,n),则随机变量X的熵定义为:
(1)
信息熵主要是反应信息的不确定性,在机器学习中,它的一个很重要的作用是可以为做决策提供一定的判断依据。
在概率学和统计学上,经常会使用一种更简单的、近似的分布来替代观察数据或太复杂的分布。KL散度能度量使用一个分布来近似代替另一个分布时所损失的信息。
相对熵又称互熵、交叉熵、鉴别信息、Kullback熵[11]、Kullback-Leible散度(即KL散度)等。设P(x)和Q(x)是X取值的两个概率概率分布,则P对Q的相对熵为:
(2)
相对熵突出的特点是非对称性[12],也就是D(P||Q)和D(Q||P)是不相等的,但是表示的都是P和Q之间的距离,在本文算法设计中采取两者的平均值(DSKL)作为两个簇或者类之间的距离,即
(3)
在聚类过程中,假设要聚类的数据为:X={X1,X2,…,Xn-1,Xn}。X是n个Rx(x=1,2…,m-1,m)空间的数据。其基本的分布见表1。

表1 数据分布表
在以上的数据分布中,每一个Xi所对应的m都不完全相同,并且数据的稀疏性很大。设N是数据集的个数,M是每个数据的最大空间维度,V表示非零数据的个数,K表示此数据集的稀疏度。则
(4)
通常认为K<5%的时候,可以将这类数据集归纳为稀疏性数据。
2 基于KL散度的聚类算法(KL-cluster)
2.1 数据预聚类
首先,扫描整体数据,对稀疏数据集上的数据进行整体的预聚类。预聚类是完成对整体数据所属类别的确定,可以在整体上分析数据[13]。在确定好具体的类别数目后,就可以对每个簇中的数据所属类别进行处理。从而为形成概率矩阵提供依据。所以预聚类的结果直接影响到以后的聚类效果。
在进行预聚类的时候,最为关键的就是聚类数目的确定。在文献[1]中,提供了一种基于层次思想的计算方法,即COPS。摒弃了传统的针对数据集的反复聚类,而是先扫描整体数据集,获得聚类特征值,然后自底向上地生成不同层次的数据集划分,增量地构建一条关于不同层次划分的聚类质量曲线Q(C),曲线极值点所对应的划分用于估计最佳的聚类数目。为此,在数据的预聚类阶段采用了此种方法,对数据的整体分布进行分析。通过预聚类形成的Q(C)曲线,可以直观的看到每个数据分布的依赖性、噪音影响以及边界模糊等情况。为确定每个数据集的聚类数目提供良好的依据,同时为概率矩阵和KL矩阵的构建提供精确的标准。完整的设计过程可以参考文献[1]。
2.2 基于KL散度的聚类过程
在聚类过程中,首先根据预聚类形成的类别数目,将每个簇中的数据进行分类,然后统计每个簇中的数据在预聚类形成的类别上的频率,形成整体数据集上的概率矩阵[13](probabilistic matrix,PM)。然后根据概率矩阵计算任意两个簇之间的距离矩阵,KL距离矩阵[14](distance matrix,DM),根据距离矩阵,将距离矩阵中的最小的两个簇合并,再次在新形成的数据集上构造概率矩阵和距离矩阵。重复以上的步骤。通过以上的递归调用,最后构造出来的距离矩阵无法指导数据合并,此时完成聚类。
2.2.1 概率矩阵的形成过程
通过预聚类过程,离散数据集上的数据分为k(k=1,2…,k-1,k)类。然后循环统计各簇中的数据在k类数据上分频率分布,这样就会形成一个n×k的概率矩阵。通过这样的方法就可以将稀疏数据根概率分布,集中在k类上,可以完成对稀疏性数据第一步收敛,减少稀疏性的弊端。形成的概率矩阵如式(5)所示:
(5)
2.2.2 距离矩阵的形成过程
根据以上的概率矩阵,分别计算矩阵中任意一行和其他一行之间的KL距离,形成整体数据集上的KL矩阵。在KL散度介绍中也谈到了KL具有非对称性,这里采用任意两行相互计算距离的平均值作为实际的KL值[14]。剩下的部分都用0来填充,最后形成如式(6)所示的上三角概率矩阵[15]:
(6)
式(7)中:DM12的计算方式如式(7)所示:
(7)
通过形成的KL矩阵,将距离矩阵中小于一定精度的值所代表的两行数据合并[16]。通过以上过程完成对数据集的一次合并,形成新的数据集。对合并后形成的数据集,按照上面的过程形成新的概率矩阵和距离矩阵,再次完成数据的合并。通过不断地重复,直到KL矩阵无法达到合并数据的精度后,完成所有数据集的聚类[17]。具体的算法流程如下如图1所示。
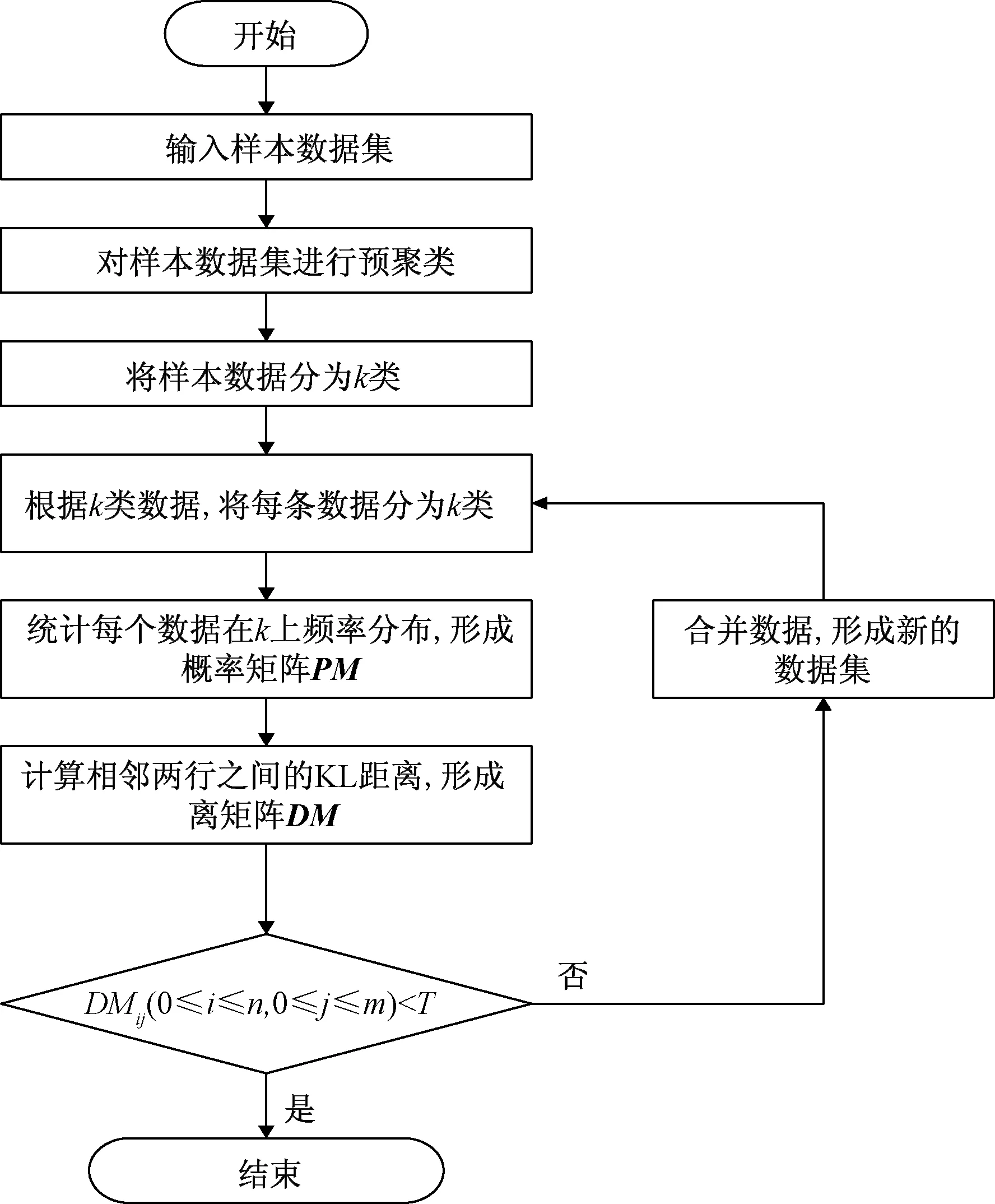
图1 KL聚类算法流程图
KL_cluster算法:

表2 KL聚类算法
3 实验与分析
3.1 数据选择
为了验证本算法的有效性,并且本算法主要针对的是离散性数据集。一方面,引用公开数据集MovieLens中最新的数据,ML-Lastest-Small和Yahoo Music作为数据集。另一方面,在The MovieDB中下载数据,然后将数据清洗、整理,得到179位观众对国内外将近180部电影评分的数据集,这里简称为MVD。来验证算法的有效性。数据基本情况见表3。
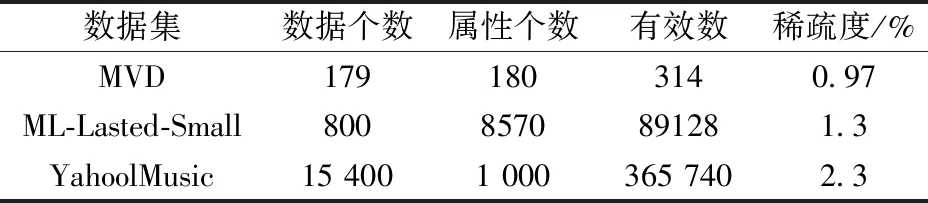
表3 数据基本信息
3.2 过程分析
3.2.1 算法评价指标
在算法准确率上,使用本文算法和常用的K-Means算法以及K-Prototypes算法进行对比,同时也使用误差平方和指标(SSE)进行评判。具体的误差平方和计算公式如式(8)所示:
(8)
式(8)中:x表示数据集中数据;μ表示类的中心点。通过此方法可以评估出聚类中心的准确度。
3.2.2 预聚类分析
首先对每个数据集上的数据集进行预聚类。根据文献[1]的方法。得到的实验结果如图3和图4所示。
通过预聚类,可以发现,聚类数目从最优变化到变到两边次优的时候,聚类质量发生大幅度下降。在图2和图3中,可以明显看到有两个基本重合的簇,数据存在一定的关联性。而通过这种方法可以很好的监测出数据依赖关系,同时为预聚类提供正确的结果。图4中,在达到最佳的聚类数10之前,曲线的变化很小,说明数据由于密度分布不均匀、边界模糊的情况,尤其是在聚类数目达到8的时候,Q(C)曲线出现了一定的上升趋势。

图2 MDB的预聚类结果
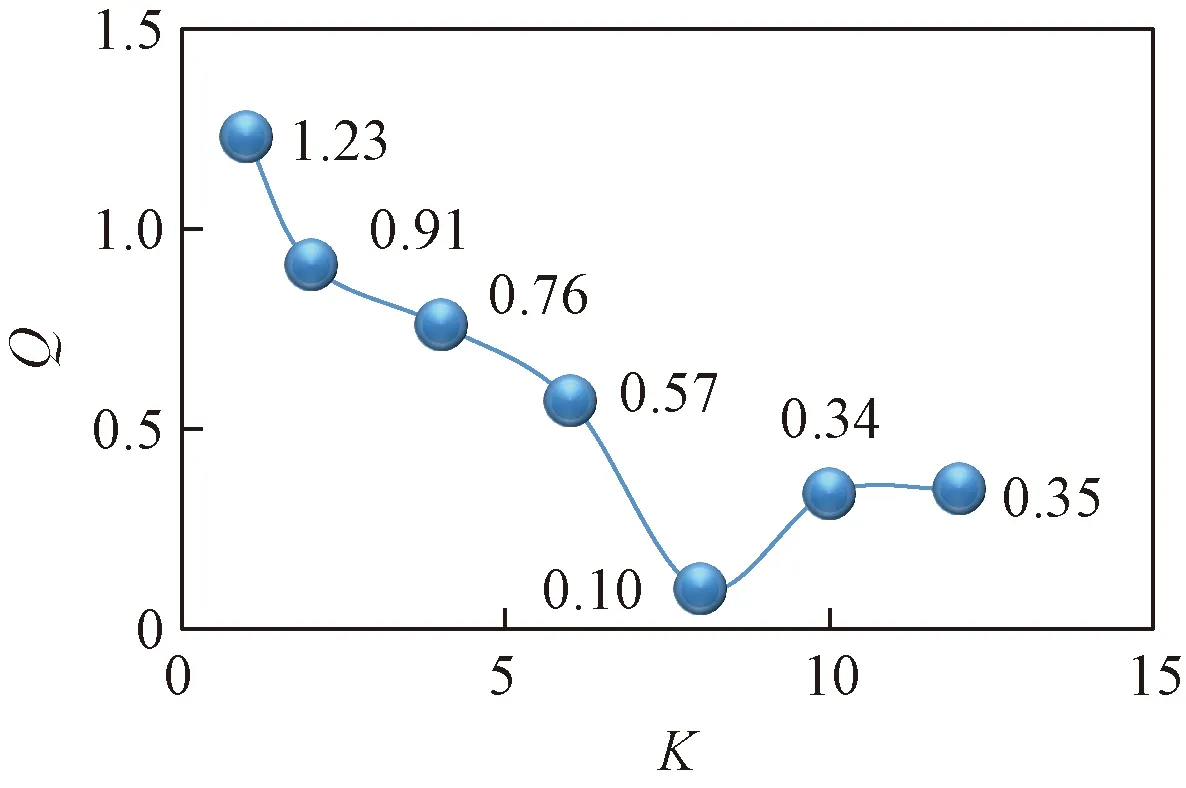
图3 MovieValue的预聚类结果
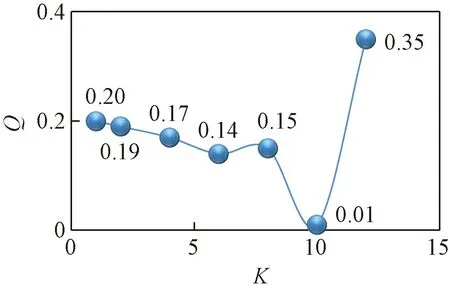
图4 MovieValue的预聚类结果
通过以上分析,预聚类过程中充分考虑了数据分布的特点,为整体的数据集类别划分提供非常精准的依据。
3.2.3 实验结果对比分析
通过实验,将本文提出的基于KL距离的聚类算法、K-Means以及K-Prototypes进行对比,其结果见表4。
本文算法与K-Means以及K-Prototypes运行时间的对比见表5。

表4 SSE对比分析
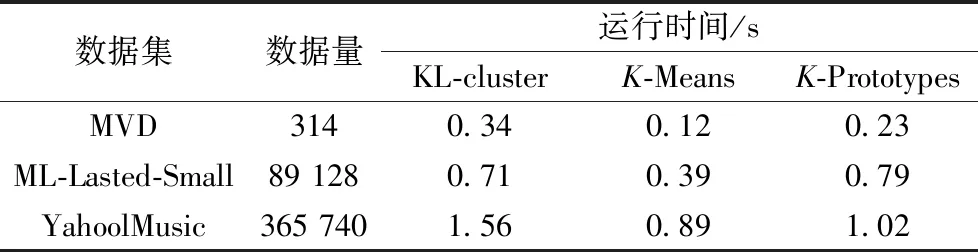
表5 运行时间对比
从以上的实验结果可以看出,KL-cluster算法相比于传统的K-Means和K-Prototypes,聚类的准确度上有了明显的提高。而运行时间在某种程度上增加,时间差距在0.08~0.67 s。原因是在预聚类中占用了一段时间,虽然牺牲了一定的时间效率,但是针对稀疏性的数据集上的聚类质量得到大幅度的提高。
4 结语
聚类算法是机器学习[18]中经常使用的一类算法,传统的K-Means算法并不能很好的处理数据稀疏性问题,在聚类的质量上产生严重的误差。为了解决此问题,提出了一种基于KL散度[19]的聚类算法。算法首先通过预聚类综合考虑了数据的分布情况,然后对将整体的数据进行聚类,划分类别。然后根据的数据分布情况构建概率矩阵,计算KL矩阵。最后通过KL矩阵知道数据聚类。通过这样的迭代过程完成聚类[20]。通过这种方式可以减少序言中提到的三个问题,提升对稀疏数据集中聚类质量和效率[21]。
