基于增量动力分析方法的单层球壳结构强震损伤分析

冯冲冲， 朱南海， 贺小玲

(江西理工大学建筑与测绘工程学院，赣州 341000)

随着中国建筑钢结构行业的不断发展，网壳结构在大型体育馆、火车站等结构中广泛应用，其一旦遇到突发偶然载荷引起构件的失效行为，将造成结构局部连续破坏甚至整体倒塌[1-5]。实际工程中大跨钢结构建筑倒塌事故时有发生，例如美国福特市的体育馆网架结构发生坍塌、法国戴高乐机场因顶棚穿孔而发生倒塌、德国巴特哈尔溜冰场因大雪压顶而发生倒塌等，造成了大量的人员伤亡。大跨度钢结构倒塌现象表明，尽管该类结构冗余度较高，但结构某些薄弱部位或者关键构件的损伤给结构整体埋下了巨大的安全隐患。

增量动力分析方法(incremental dynamic analysis,IDA)是在1977 年由Bertero提出，后在2000年被美FEMA所采用。卜一等[6]以高层混合结构为研究对象，采用IDA方法研究并给出了该类型结构的抗震性能水准。吕大刚等[7]基于IDA方法并提出“折半取中”原则，确定结构倒塌极限状态点，并指出杆件屈服后对结构极限承载力影响较显著。冯俊迎等[8]以桥梁为研究对象，采用IDA方法得出LRB能起到保护桥梁的作用。Khorami 等[9]采用IDA 方法分析并比较同心支撑框架和屈曲约束支撑框架的抗震性能，结果表明屈曲约束支撑框架的抗震性能较好。陆新征等[10]采用IDA和地震易损性分析了两个算例，指出仅考虑单向地震波会高估结构抗倒塌能力。吕西林等[11]以复杂的高层结构为研究对象，采用IDA方法建立地震易损性曲线评估结构抗倒塌的能力。王丰等[12]提出了一种基于简化的IDA方法评估结构地震损伤，并用算例得出此方法用来评估结构抗震更安全。现主要采用ABAQUS有限元分析软件，引入钢材损伤本构模型，提供更加真实的对单层凯威特网壳结构动力倒塌进行模拟，揭示结构的强震倒塌机理，并考察不同杆件尺寸、矢跨比、初始几何缺陷、支座约束等对单层网壳结构的抗倒塌能力的影响，为工程的实际应用提供参考。

1 钢材本构模型

材料的损伤是导致结构破坏的根本原因，由材料损伤逐步引起杆件破坏，最后引起整体结构失效。结构的局部甚破坏至整体倒塌通常是由构件损伤累积到一定程度后引起的[13]。损伤理论从基于材料的强度和变形之间的本构关系出发，研究材料在简单受力(单轴拉伸、压缩)及复杂受力(多轴受力)状态下的力学特性，从微观层次上定义损伤。

研究结构损伤破坏的关键就是材料的损伤本构模型，合理地选用材料本构模型能够更精确地模拟结构构件在荷载作用下的强度、刚度不断退化和损伤演化破坏的全过程。

构件本身含有不同形式的细观缺陷，在地震作用下，这种细观缺陷对整体结构的影响不断放大，因此需考虑材料损伤累积的影响。对于延性金属在微观尺度上的损伤，其微观机制在于微观缺陷的形成[14]，因此强震作用下，考虑材料损伤累积能准确模拟出结构实际的动力响应。在整个分析过程中，损伤因子不断递增，即损伤过程不可逆。此处引入定义的材料损伤模型计算[15]。

(1)

损伤对钢材性能的影响可表示为

ED=(1-ξ1D)E

(2)

σD=(1-ξ2D)σs

(3)

式中：E和ED分别为结构考虑损伤前后的弹性模量；σs和σD分别为无损及有损时结构的屈服应力；对于Q235钢，ξ1为0.277；ξ2为0.119。

在加载和卸载阶段，材料弹性本构可表示为

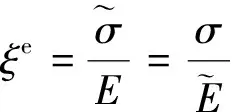
(4)

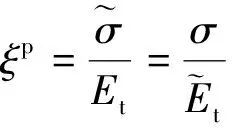
(5)

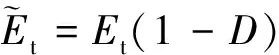
2 地震作用下网壳结构的损伤分析

地震作用下，大跨空间网壳结构的破坏过程十分复杂，因此选用地震波时，应考虑多方面的影响，以便更真实地模拟网壳结构的实际响应规律。此处将结合抗震设计规范中的相关规定及结构的地震反应谱原理，确定地震波的选择，采用时程分析法对网壳结构进行地震响应分析。

增量动力分析(incremental dynamic analysis，IDA)方法，它将一个或多个地震波按照一定比例 “调幅”为不同的地震波强度并输入到结构模型中，通过逐步增加地震波强度指标IM(如地震波峰值加速度PGA等)，然后对每个强度的地震动强度进行非线性动态时程分析，直到结构坍塌。 每次动力分析可获得结构响应峰值DM(如结构的最大节点位移等)。最后，从DM和IM的参数获得IDA之间的关系曲线。

网壳结构倒塌判别准则采用动力强度准则，即在动力荷载作用下，网壳的最大位移达到结构跨度的1/100，并当结构达到屈服的杆件比例超过42%时，网壳达到其极限承载力并将发生倒塌破坏[16]。

2.1 地震波的选取与调整

如图1所示跨度为50 m的K6N6型单层凯威特网壳结构，采用IDA分析方法对其在地震作用下的非线性行为进行分析。考虑地震波的随机性，选择持时15 s的El-Centro波(图2)分析该结构在三向地震作用下(其X∶Y∶Z=1∶0.85∶0.65)的动力破坏过程。

图1 网壳跨度50 m的K6N6结构模型Fig.1 Reticulated shell span 50 m, K6N6 structural model

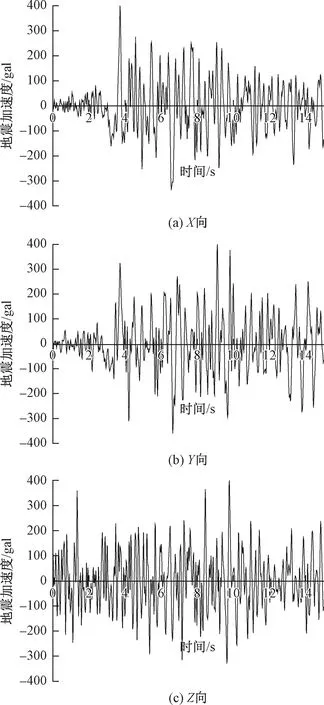
1 gal=0.01 m·s-2图2 三向EL-Centro波时程曲线Fig.2 Three-way EL-Centro wave time history curve

网壳周边刚接，阻尼比为0.05。材料弹性模量为2.1×1011Pa，泊松比为0.3，屈服应力为345 MPa，密度7 850 kg/m3，采用一致缺陷法，考虑材料非线性，初始缺陷取结构跨度的1/300。结构采用全梁单元建模，并采用IDA分析方法逐步提高输入的地震加速度幅值，对地震作用下网壳结构的位移响应、结构塑性单元的比例及其塑性发展过程进行分析研究，直至结构发生失效。

采用式(6)对地震加速度幅值进行调整。

(6)

式(6)中，a(t)为调整前地震波时程PGA曲线，amax为调整前PGA峰值，a′(t)为调整后地震波时程PGA曲线，a′max为调整后PGA峰值。以8度罕遇地震对应的加速度幅值400 cm·s-2进行调幅，每次调幅步长为25 cm·s-2，获得的IM与DM(最大节点位移及结构塑性单元比例)的关系曲线。

2.2 不同杆件截面尺寸的影响

取结构矢跨比为1/5，初始缺陷为L/300，杆件截面尺寸分别采用①Φ0.16 m×0.005 m、②Φ0.14 m×0.0045 m、③Φ0.12 m×0.004 m(直径×厚度)，采用El-Centro三向地震波对该结构进行抗倒塌性能分析，其结果如图3所示。

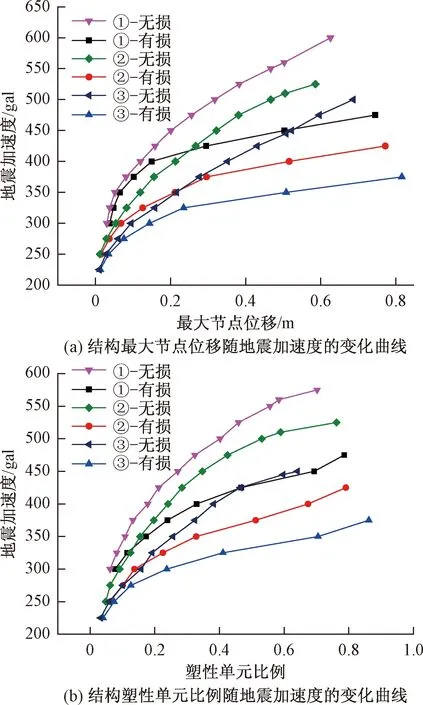
图3 不同杆件截面强度的结构IDA曲线Fig.3 Structure IDA curve of the cross-section strength of different rods

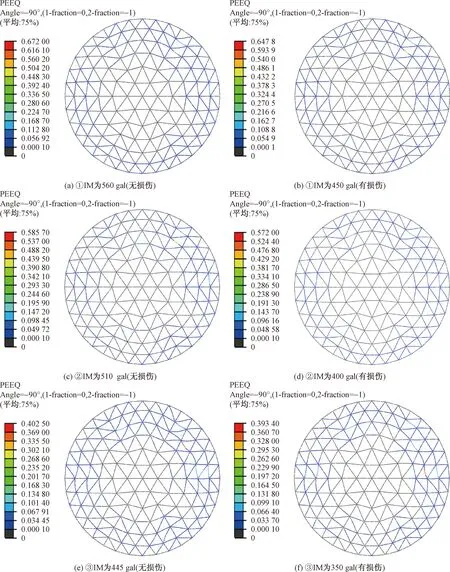
PEEQ为等效塑性应变图4 不同杆件截面尺寸的结构塑性分布Fig.4 Structural plasticity distribution of cross-section dimensions of different rods

从图3可知：当其他参数一定时，随结构杆件截面的加强，结构在强震下的抗倒塌极限承载力明显提高。在地震强度达到280 gal左右时，各结构的部分单元进入塑性，随后，结构的塑性发展及最大节点位移开始显著增长，这是由于随地震强度的提高，结构已经有较多单元发生屈服，塑性杆件数量逐渐增大，最后达到网壳极限承载力发生倒塌。依据动力强度破坏准则，不同杆件截面结构有无损伤的动力极限响应指标如表1所示。由表1可知，对其有相同参数的结构，当结构达到极限承载力时，考虑损伤的结构塑性单元比例均比未考虑损伤的结构高10%左右，因此不可忽视材料损伤累积的影响。由图3得知，地震强度较小时，不考虑与考虑损伤累积计算所得塑性单元比例相似，随后塑性单元比例相差明显加大，考虑损伤累积效应后，局部易损部位进入塑性的单元数量比例明显提高，在整体结构还能继续承载的情况下，局部微观部位已经由于材料刚度及强度的劣化逐渐引起构件破坏直至结构局部大面积失效。本文由于篇幅的原因，故只给出网壳结构在倒塌极限荷载时的塑性发展图(图4)，可知，结构塑性发展最大部位主要集中在结构底部的第一至第四环内。

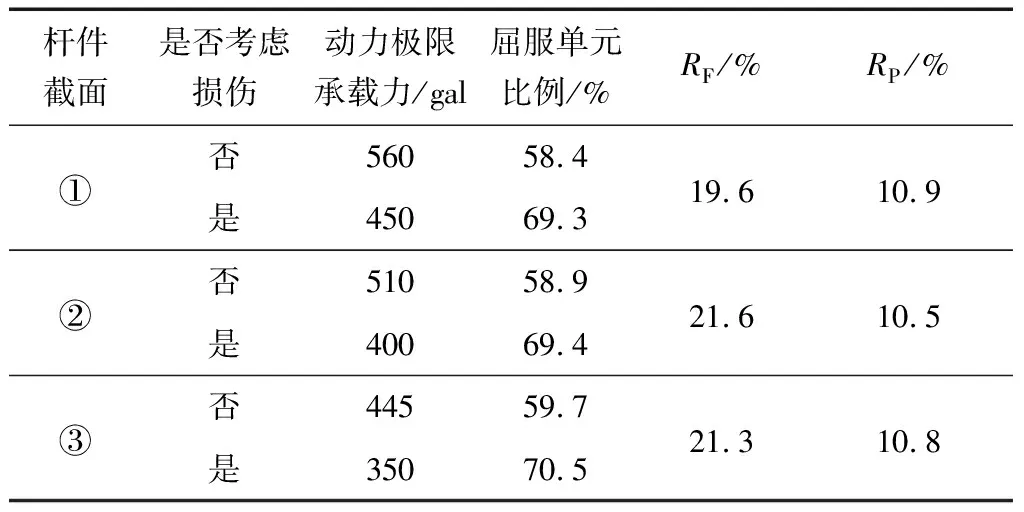
表1 各类截面结构的动力极限响应指标

注：RF为考虑损伤后结构动力极限承载力的下降比例，RP为考虑损伤后结构塑性单元上升比例。

2.3 不同矢跨比的影响

结构跨度保持不变，初始缺陷为L/300，矢跨比分别采用 1/6、1/5、1/4，杆件截面尺寸采用同一型号的圆钢管，均为Φ0.08 m×0.005 m，采用El-Centro三向地震输入分析矢跨比对结构抗倒塌性能的影响，计算结果如图5所示。

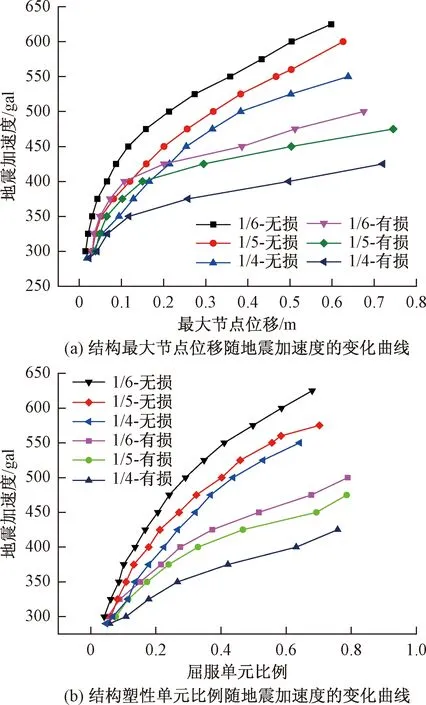
图5 不同矢跨比的结构IDA曲线Fig.5 Structure IDA curves for different span ratios

由图5可知，当其他参数一定时，随结构矢跨比的增大，结构在地震作用下的极限承载力明显降低。不同矢跨比的网壳在地震强度达到300 gal时先进入塑性，此时塑性单元的比例较低，随后结构的塑性发展加快，节点位移显著增长，这是由于矢跨比越大，结构整体刚度明显下降，网壳在强震作用下的受力更加不均匀，结构内力重分布更加明显，故在强震作用下微小的荷载增长，材料损伤累积的影响进一步提高，塑性单元发生屈服的区域明显扩大，直至结构倒塌。依据动力强度破坏准则，不同杆件截面结构有无损伤的动力极限响应指标如表2所示。由图6可知，结构塑性发展最大的部位主要集中在结构底部的第一至第四环内。

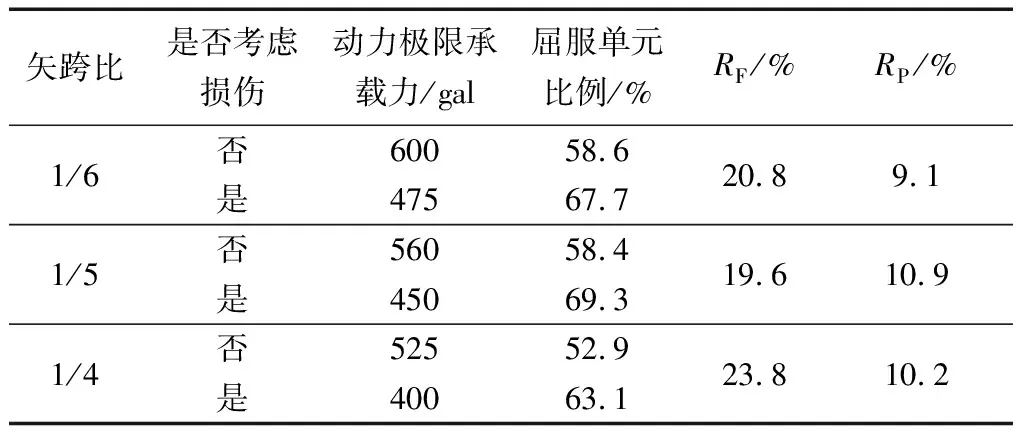
表2 不同矢跨比结构的动力极限响应指标

2.4 不同初始缺陷的影响

同理，取结构矢跨比为1/5，截面尺寸均为Φ0.08 m×0.005 m，初始缺陷分别为0、L/500、L/400、L/300、L/200、L/100，采用一致缺陷法，同样采用El-Centro三向地震动分析结构初始缺陷对其抗震性能的影响，其结果如图7所示。

图6 不同矢跨比的结构塑性分布Fig.6 Structural plasticity distribution of different span ratio

图7 不同初始缺陷的结构地震极限承载力变化曲线Fig.7 Structural seismic ultimate bearing capacity variation curves of different initial imperfections

由图7可得知，初始缺陷的大小对网壳抗倒塌能力的影响比较明显，随结构初始缺陷的增大，网壳的地震极限承载力明显降低，最高降低了30%左右，即初始缺陷对网壳的影响较大。对于完整结构[17]，其极限荷载较高，因为对于完整结构，壳体传力路径清晰，有利于网壳内的力重分布，使得材料损伤与杆件塑性能在整个结构内充分发展。然而初始缺陷的引入，相当于在结构的表面预先形成一个塑性薄弱区，此薄弱区域破坏了结构原有的传力路径，造成杆件截面应力与结构变形集中，内力重分布首先发生在结构的局部，随着退出工作的杆件的增加，内力重分布向整个网壳扩展，并局部杆件退出工作的区域损伤累积显著增大。随着初始缺陷的不断增大，结构性能劣化逐渐加速，薄弱区域杆件更快地发生断裂，进而引发结构整体倒塌，结构易发生动力失稳。由图7可知，在不同初始缺陷下在考虑损伤时的动力极限荷载比未考虑损伤时下降了20%左右。

2.5 支座约束数量的影响

结构矢跨比为1/5，初始缺陷L/300，杆件截面尺寸均为Φ0.08 m×0.005 m，支座为固端约束支座，沿结构底部节点间隔布置，其结果如图8所示。

由图8可知，当地震波幅值达到250 gal时，部分单元开始进入塑性，随后，网壳的最大节点位移及塑性单元的比例快速增长，这是由于结构底部支座约束数量大大减少，考虑材料损伤累积效应后，结构在强震下的动力稳定性急剧降低，塑性薄弱区域的材料损伤累积剧增，杆件损伤的比例明显加大，直至倒塌。依据动力强度破坏准则，在底部节点全部约束和间隔约束情况下结构的地震极限响应指标如表3所示。由图9可知，结构塑性发展最大的部位主要集中在结构底部的第一至第四环。

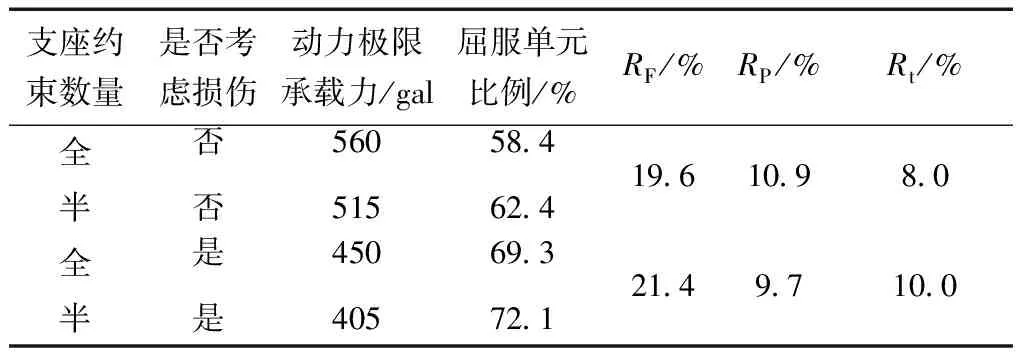
表3 不同支座约束数量结构的动力极限响应指标

注：Rt表示支座约束数量减半时有无考虑损伤的结构动力极限承载力下降的比例。

3 结论

以跨度50 m的单层球面网壳为研究对象，考虑结构的损伤累积效应，分析不同杆件截面尺寸、矢跨比、初始几何缺陷、支座约束数等参数对结构在强震作用下的损伤破坏过程进行了系统地分析，综合以上，可获得以下主要结论。

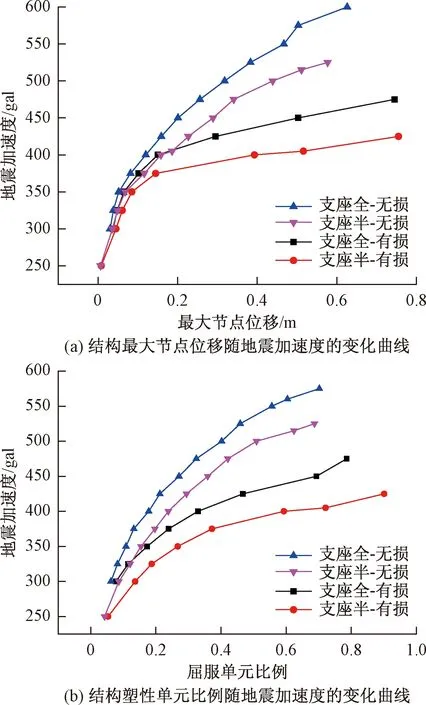
图8 不同支座约束的结构IDA曲线Fig.8 Reticulated shell IDA curve with different bearing constraints

图9 支座约束数量减半网壳塑性分布Fig.9 The plastic distribution of the reticulated shell of the number of bearing constraints reduced by half

(1)考虑损伤累积效应后其结构地震极限承载力比未考虑损伤时下降了20%左右，塑性单元的比例上升10%左右，因此在工程实际应用中应考虑材料损伤累积的影响。

(2)当其他参数一定时，随杆件截面整体强度的增大，结构极限承载力显著提升；随结构矢跨的增大，结构抗倒塌能力逐渐降低；初始缺陷对结构的抗倒塌能力影响较大，随结构初始缺陷的增大，其极限承载力最大可降低30%左右，即强震作用下的网壳对初始缺陷十分敏感，因此结构设计之初，应该注重初始缺陷的影响；在支座约束数量减半后，损伤累积效应使结构的地震承载力降低10%左右。

(3)网壳在强震作用下的抗倒塌能力。其屈服单元以及最大节点位移几乎均发生在网壳结构底部的第一至第四环内，因此在工程抗震设计时，可考虑加强此部位，以提升结构的抗倒塌能力。