混合动力车辆永磁同步轮毂电机转速自抗扰控制
2020-04-22陈路明廖自力
陈路明, 廖自力, 张 征
(1.陆军装甲兵学院兵器与控制系,北京 100072;2.陆军装甲兵学院全电化陆战平台重点实验室,北京 100072)
为缓解当前日益紧张的能源和环境危机,一些国家政府都在大力倡导发展新能源车辆,不断扩大新能源车辆应用深度和广度,力求逐步摆脱对石油等一次能源的依赖,推动全产业链清洁发展[1]。在广阔的应用前景和巨大的利益面前,各类新能源车辆受到各大汽车制造厂商的广泛关注,成为当前及未来重点研发的车型。根据动力源类型和数量,新能源车辆可以分为纯电动车辆、燃料电池车辆、氢发动机车辆及混合动力车辆等[2]。限于电池材料和管理水平,纯电动车辆在续航里程和安全性方面仍面临诸多问题;燃料电池和氢发动机车辆技术成熟度有待提高,在车辆中大范围应用仍存在一定技术难度;作为传统机械车辆与纯电动车辆之间的过渡车辆,混合动力车辆技术成熟度高,续航里程卓越,可通过合理控制实现多动力源工作优势互补,深受各汽车制造厂商青睐,成为当前中高端车辆普遍采用的结构形式。
采用分布式驱动的混合动力车辆中,永磁同步轮毂电机承担着全部动力输出任务,成为车辆动力系统的核心单元[3]。因此,电机的控制水平直接决定了混合动力车辆的动力性能。对于驱动电机的控制而言,工程开发人员尤其关注其转速响应特性[4]。通常电机运行工况复杂多变,存在各类不确定性扰动,工程上采用的传统比例积分微分(proportion integral derivative, PID)控制方法虽然实现简单,但始终存在转速超调和快速跟踪之间的矛盾,在复杂扰动条件下转速跟踪精度不高,制约了混合动力车辆动力性能的提升。基于现代控制理论的多种方法如模糊控制、滑模控制、模型预测控制等应用于电机调速控制,或需要被控对象精确数学模型,或在模型失配和外界扰动下控制性能恶化等问题[5-7]。自抗扰控制(active disturbance rejection control, ADRC)方法不依赖被控对象精确数学模型,具备扰动估计和补偿能力,控制效果较好且计算量不大,有利于提升电机控制性能。文献[8]将自抗扰控制应用于无位置传感器永磁同步轮毂电机转速控制,赋予控制器扰动估计和补偿能力,但为规避完整自抗扰控制器多参数整定的复杂问题,简化了自抗扰控制结构,控制效果是否受到影响有待验证。
本文基于文献[8]的研究思路,针对混合动力车辆永磁同步轮毂电机在各类扰动条件下转速跟踪精度不高的问题,将非线性自抗扰控制引入电机转速控制环路,并为众多控制参数提供整定方法,以期提升转速跟踪精度,降低自抗扰控制实际应用难度,为驱动电机转速自抗扰控制提供借鉴和参考。
1 永磁同步轮毂电机控制模型
1.1 电机数学模型
在电动机惯例下,建立永磁同步轮毂电机在两相旋转坐标系下的数学模型[9]。
定子磁链方程:
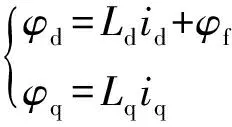
(1)
式(1)中:φd和φq分别为定子直轴和交轴磁链;Ld和Lq分别为定子直轴和交轴电感;id和iq分别为定子直轴和交轴电流;φf为转子永磁体磁链。
定子电压方程:
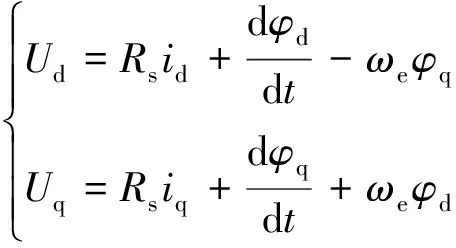
(2)
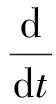
电磁转矩方程
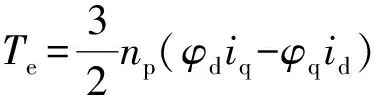
(3)
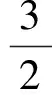
机械运动方程:
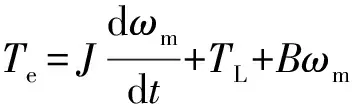
(4)
式(4)中:J为转动惯量;ωm为机械角速度;TL为负载转矩;B为黏滞摩擦系数。
1.2 双闭环控制结构
典型的永磁同步轮毂电机调速系统的双闭环控制结构如图1所示。
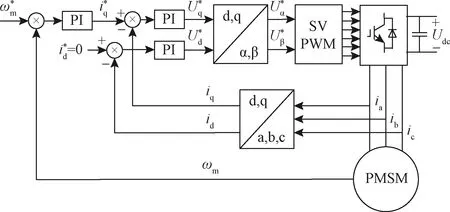
图1 永磁同步轮毂电机双闭环控制结构Fig.1 Permanent magnet sychronous wheel hub motor dual closed-loop control structure
永磁同步轮毂电机转速控制结构由外部转速控制环路和内部电流控制环路组成,其中转速外环主要功能是稳定电机输出转速,将控制器给定的目标转速和转速传感器检测的实际转速的差值经PI处理,得到电流内环的目标电流;电流内环主要功能是稳定逆变器交流侧电流,通过将电压外环给定的目标电流与电流传感器检测的实际电流的差值经PI处理,得到静止两相坐标系下的目标电压,经空间矢量脉冲宽度调制(space vector pulse width modulation, SVPWM),得到六路三桥臂逆变器的开关管控制信号,实现完整的双闭环控制过程。
2 自抗扰控制原理
自抗扰控制是由韩京清研究员自主提出一种新型控制方法,这种方法不依赖于被控对象的精确数学模型,可以仅仅依靠测量的输入输出关系,高效地抑制各类扰动,具有较强的鲁棒性和较高的控制精度[10]。典型的二阶自抗扰控制器结构如图2所示。
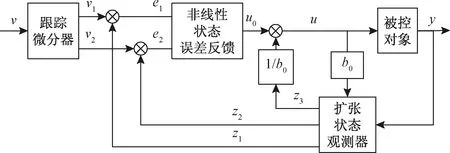
图2 典型二阶自抗扰控制器结构Fig.2 Typical second order active disturbance rejection control structure
自抗扰控制器主要由四个功能模块组成,各模块实现原理如下[11]。
2.1 跟踪微分器
跟踪微分器(tracking-differentiator, TD)能够从突变或污染信号中过滤得到目标信号,合理安排过渡环节使过渡信号能够快速无超调地跟踪给定值,同时可以给出该过程的微分信号。
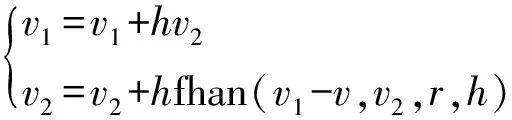
(5)
式(5)中:v、v1和v2分别给定量、安排过渡量及其微分信号;fhan 为离散系统最速控制综合函数,r为跟踪微分器的速度跟踪因子;h为离散采样时间。
离散系统最速控制综合函数fhan 的展开式为
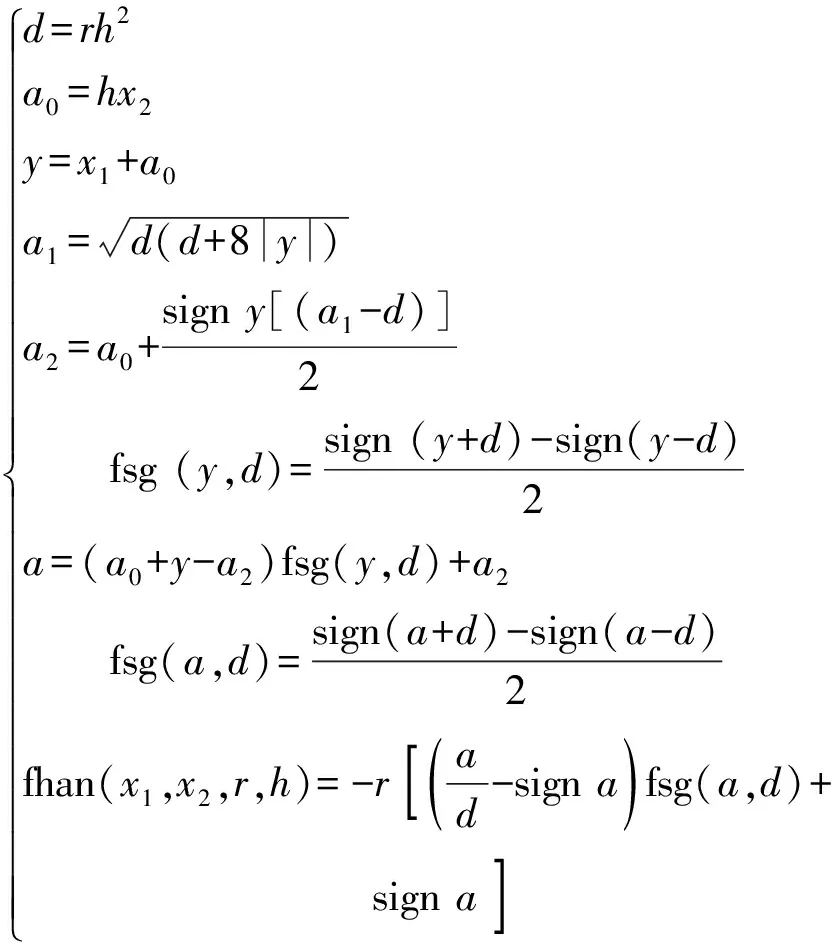
(6)
式(6)中:d、a、a0、a1、a2、x1、x2和y为自定义过程变量;fsg 为自定义过程函数;sign 为通用符号函数。
2.2 扩张状态观测器
扩张状态观测器(extened state observer, ESO)能够以观测状态变量快速跟踪系统输出状态、微分,并能够扩展状态变量得到系统的总和扰动。
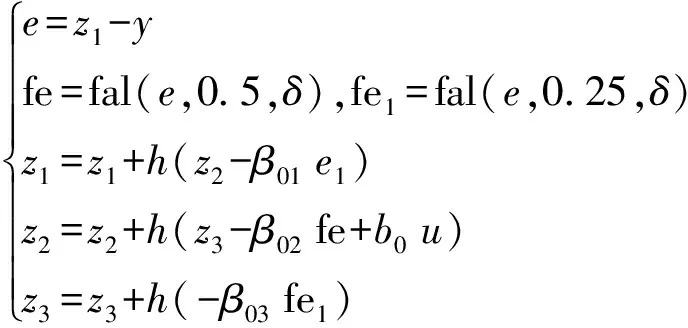
(7)
式(7)中:e为扩张状态观测量对输出信号跟踪量与输出信号差值;fal为通过原点包含线性区域的幂次函数;fe 和fe1分别为不同参数下fal 的输出量;z1和z2分别为输出量观测值及其微分信号;z3为扩张的总和扰动估计量;β01、β02和β03为各阶控制增益。
过原点包含线性区的幂次函数fal 的展开式为
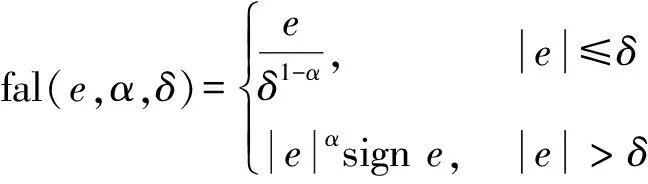
(8)
式(8)中:α为与观测状态变量阶数有关参数;δ为线性段区间长度。
2.3 非线性状态误差反馈控制
非线性状态误差反馈控制(nonlinear state error feedback, NLSEF)通过对误差及其微分信号进行非线性组合,可以得到效果较好控制效果。
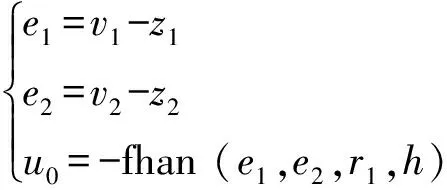
(9)
式(9)中:e1为过渡过程量与输出观测量的误差;e2为过渡过程量微分与输出观测量微分的误差;u0为初始控制量;r1为非线性状态误差反馈控制律的速度跟踪因子。
2.4 扰动估计补偿
扰动估计补偿通过误差状态补偿校正,可将非线性系统转化为积分器串联型线性系统进行处理。
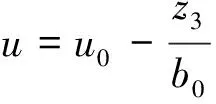
(10)
式(10)中:u为经补偿后的实际控制量,b0为综合扰动调整系数。
3 永磁同步轮毂电机自抗扰控制器设计
3.1 控制器设计
通常,电流内环的带宽远大于电压外环带宽,且二者相差通常在一个数量级以上,为保证电流内环响应的强实时性,减轻处理器计算压力,因此电流内环仍延续经典PI控制;由于转速控制效果主要取决于外环控制优劣,因此研究中仅考虑将自抗扰控制应用于电压外环控制,在提升控制效果的同时尽量减小计算压力。
在明确研究对象和控制回路后,依据电机数学模型来推导相关变量关系。将式(3)和式(4)联立,可得:
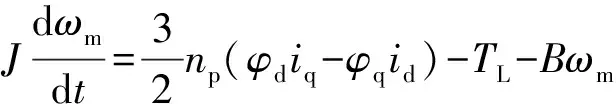
(11)
由于研究永磁同步轮毂电机为表贴式,最优控制方式即最大转矩电流比控制此时等同于将全部相电流is作用于交轴电流iq,直轴电流id置零,因此式(11)可以简化为
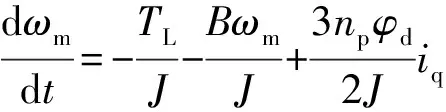
(12)
取ωm为状态变量x,iq为控制变量u,取y为输出变量,可将式(12)转化为标准自抗扰研究对象形式:
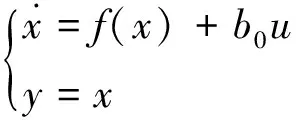
(13)
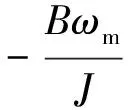
由于被控对象为一阶系统,理论上完全可以采用经典一阶自抗扰控制器进行设计,但由于一阶自抗扰控制中仅仅考虑跟踪量与观测量的误差作用,没有考虑跟踪量微分与观测量微分的误差作用,而微分量具有一定“预报”功能,为充分考虑各项影响因素,提高控制效果,因此采用经典二阶自抗扰控制器来处理一阶被控对象。
3.2 参数整定方法
二阶自抗扰控制器存在很多需要整定的参数,且部分参数缺乏明确的物理意义或参数之间缺乏明确的指导关系,参数整定始终是自抗扰控制器设计过程中不可回避的难题。虽然不同功能模块组合在一起构成了自抗扰控制器,但自抗扰控制器参数整定却可以在不同功能模块独立进行,即自抗扰控制器设计中的“分离性原理”[12]。
在控制器设计中,离散采样时间h通常提前确定,在此基础上,可进一步考虑各类与离散采样时间h有相关性的参数及无相关性的参数整定问题。
跟踪微分器中需要整定的参数是r。r取值越大,系统跟踪速率越快,反之亦然。因此r可按照式(14)取值:
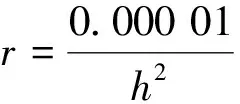
(14)
扩张状态观测器中需要整定的参数是β01、β02、β03、δ。系统动态特性主要由β03确定,取值越大,跟踪滞后越小,反之取值越小,跟踪滞后越大,但是当它取值过大时,会造成跟踪振荡,可以通过调节β01和β02减小振荡,得到优质跟踪效果;δ可与h大小保持一致。因此,各参数可按照式(15)取值:
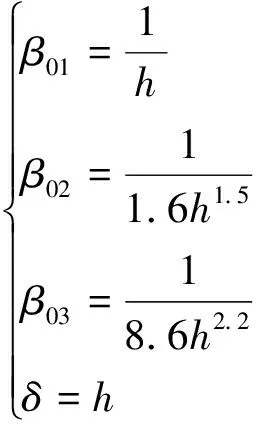
(15)
非线性状态误差反馈控制律中需要整定的参数是r1。r1取值较大,系统调节速度加快,反之r1取值较小时,系统调节速度减慢。
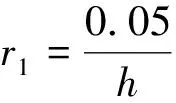
(16)
扰动估计补偿中需要整定的参数是b0。b0是一个既与控制量又与扩张状态观测器有关的参数。当被控对象数学模型已知时,可直接得到;当数学模型未知时,在真值30%附近选取都可以得到较好的控制效果。由于被控对象数学模型明确,因此有:
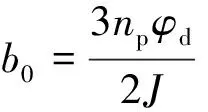
(17)
4 仿真研究
为验证自抗扰控制策略的有效性,在MATLAB/Simulink中搭建三相永磁同步轮毂电机仿真模型,电机参数设置如表1、表2所示。

表1 永磁同步轮毂电机参数Table 1 Permanent magnet sychronous wheel hub motor parameter
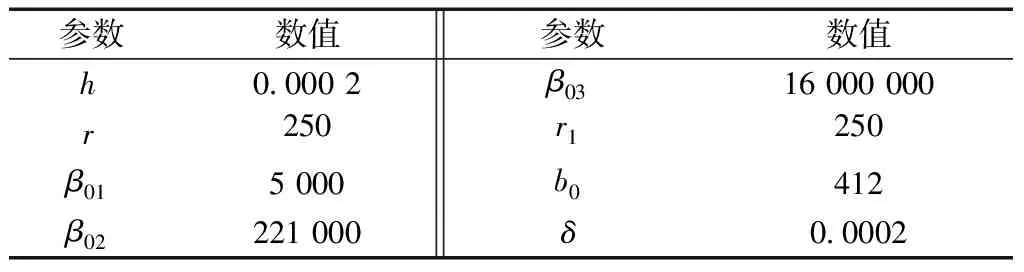
表2 自抗扰控制器参数Table 2 Active disturbance rejection control parameter
搭建得到的仿真模型如图3所示。
4.1 负载转矩扰动实验
电机带载运行时,负载转矩通常不可预知,当负载转矩发生扰动时,势必会影响转速的稳定精度。为考察电机在负载转矩调整时实际转速的响应情况,在最恶劣的负载转矩大幅阶跃实验条件下,得到图4所示仿真结果。
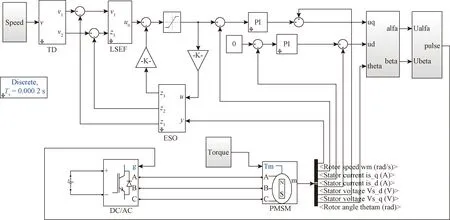
图3 永磁同步轮毂电机仿真模型Fig.3 Permanent magnet sychronous wheel hub motor simulation model
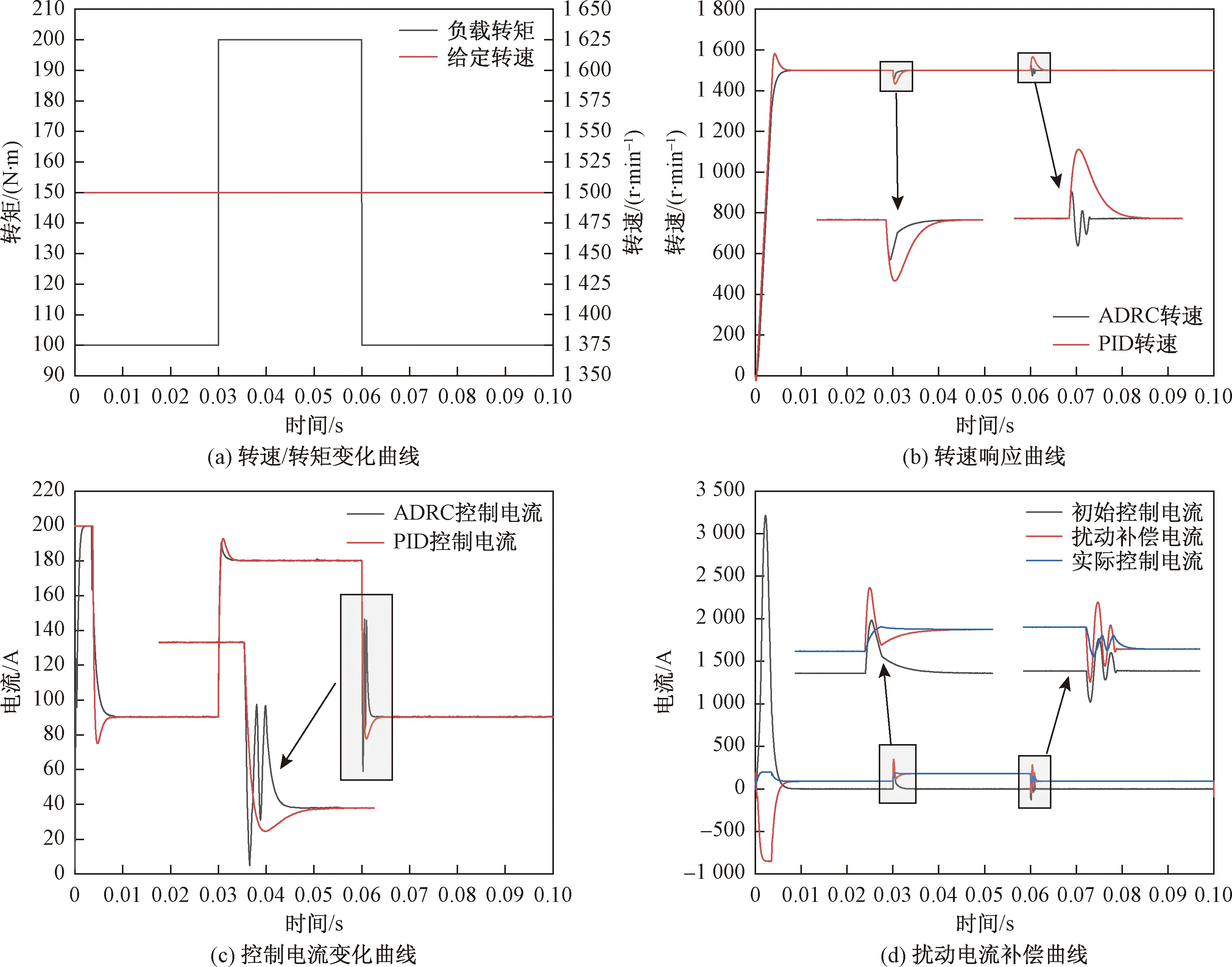
图4 负载转矩扰动仿真实验结果Fig.4 Load torque disturbance simulation experiment results
由图4(a)可知,实验过程中电机输入端设定为1 500 r/min的恒定给定转速,分别在0.03 s和0.06 s负载转矩完成100~200 N·m和200~100 N·m两次上下阶跃,观察零初始转速电机在ADRC和优化调整参数的PID控制下的状态响应情况:由图4(b)电机转速跟踪情况来看,在加载条件下ADRC控制出现40 r/min左右转速跌落,经过0.003 s无超调回到稳态,而PID控制出现70 r/min左右转速跌落,经过0.004 s无超调回到稳态,在减载条件下出现25 r/min左右转速跃升,经过0.001 s衰减振荡回到稳态,而PID控制出现70 r/min左右转速跃升,经过0.004 s无超调回到稳态;由图4(c)控制电流变化情况来看,在转矩阶跃调整时,ADRC和PID变化速率基本一致,在加载条件下ADRC控制电流超调量小于PID,但在减载条件下ADRC控制电流出现剧烈震荡,由图4(d)可知,此时ADRC在允许范围内以小幅转速稳定性损失实现了极佳的动态调整快速性。
4.2 模型失配扰动实验
电机工作环境和自身温度都在时刻发生变化,同时电机参数也在时刻进行调整,严格来讲是电机处于一个非线性的工作过程,这种参数调整会造成模型失配,给控制效果造成不利影响。为考察已有控制策略在模型失配条件下的控制效果,人为设定电机参数调整量,得到如图5所示仿真结果。
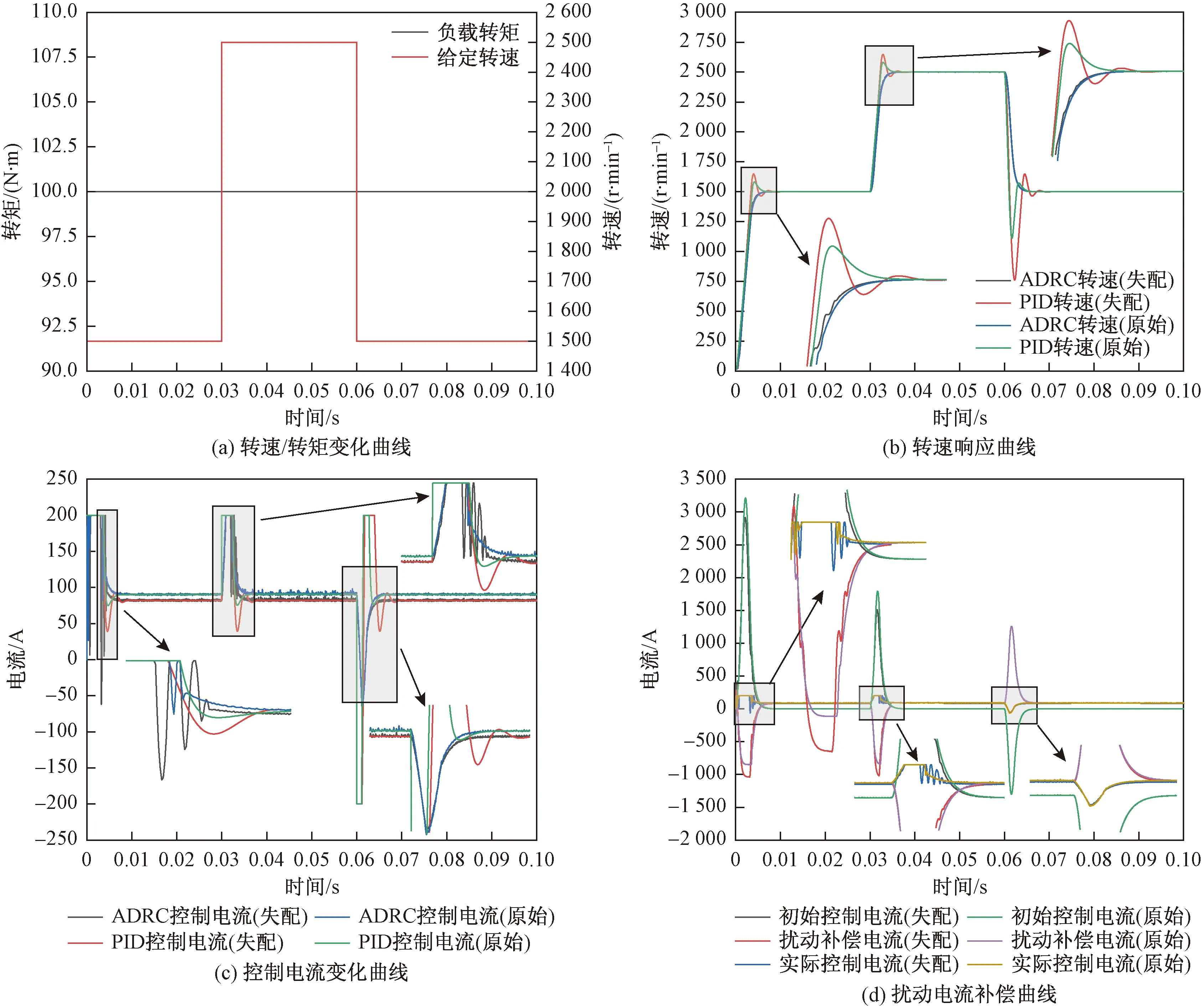
图5 模型失配扰动仿真实验结果Fig.5 Model mismatch simulation experiment results
参数设置为:相电阻调整为原来的500%,即0.032 8 Ω;定子电感调整为原来的200%,即0.79 mH;磁通量调整为原来120%,即0.204 174 V·s。由图5(a)可知,在恒定100 负载转矩条件下,施加相同转速阶跃给定信号,考察控制器在失配前后的响应效果;由图5(b)可知,在模型失配后,PID控制下超调量明显增加,且振荡次数增多,而ADRC前后响应效果几乎无差别,保持了良好的动态响应效果;由图5(c)可知,在模型失配后,PID控制电流响应时间有所延长,且控制量超调增加,ADRC振荡幅度和次数增加,加快了动态响应过程;由图5(d)可知,相较模型未失配的情况,ADRC在失配后扰动电流补偿幅度和频率增加,同时实际控制电流变化同步发生变化,加快了失配条件下的动态调节能力,极大消除了模型失配对转速跟踪的影响。
5 结论
(1)针对混合动力车辆永磁同步轮毂电机在负载转矩等外部扰动条件下转速跟踪效果不佳的问题,将自抗扰控制引入转速控制外环,加快了转速响应速度,提升了转速跟踪精度,降低了转速超调。
(2)针对模型失配造成的内部扰动,基于自抗扰控制的转速控制,可实时估计总和扰动,补偿控制输入,表现出优越的控制性能。
(3)针对多个控制参数整定困难问题,依据经验公式计算得到各参数初始控制参数值,且不需要优化调整即具备较为优越的控制性能。表明自抗扰控制器对控制参数具有较强的鲁棒性。
